滑动聚束SAR 空变天线方向图校正方法①

胡继伟,党红杏,贺荣荣

(中国空间技术研究院西安分院,西安 710000)

0 引言

在SAR 系统中,条带模式和聚束模式是两种最常用的工作模式。 条带模式能进行连续大面积成像,但系统的方位分辨率不能随天线尺寸减小而任意提高。 聚束模式通过控制雷达天线波束方向连续指向某一特定区域,使回波信号相干积累时间骤增,能实现高方位分辨率,但该模式只能对一小块区域成像,无法实现大面积的高分辨率成像。 为实现大面积高分辨率成像,滑动聚束SAR 作为一种新颖的工作模式应运而生。 它通过控制天线辐照区在地面移动的速度增加方位向相干积累时间,从而获得较相同尺寸天线条带SAR 更高的方位分辨率,较聚束SAR 更大的成像面积。 目前,国外先进的SAR 系统如 PAMIR、TerraSAR-X 等均采用了该成像模式[1-4]。

滑动聚束SAR 工作时,通过控制天线波束前扫和后扫来增加方位向相干积累时间,从而可以提高SAR 系统方位向分辨率,但同时,这种波束指向的不断变化也带来了新的问题:传统条带模式波束指向是固定的,SAR 天线方向图对于测绘带内相同距离向的不同目标加权是一致的,但滑动聚束模式下,由于天线波束指向的不断变化,导致SAR 天线方向图对于测绘带内即使相同距离向的不同目标加权也是不同的,即SAR 天线方向图对于观测区域SAR 图像的加权在距离向和方位向是二维空变的。 滑动聚束模式下天线方向图的二维空变特性将导致采用传统SAR 天线方向图测量和校正方法会引入误差,影响SAR 辐射定标精度及目标后向散射系数测量精度[5-8]。

本文基于滑动聚束SAR 仿真数据对滑动聚束模式下SAR 天线方向图二维空变特性进行了分析,比较了观测场景内不同距离向和方位向目标点的天线方向图加权变化特性,然后建立距离向和方位向二维多项式模型来拟合SAR 天线方向图二维空变误差,最后,基于天线方向图空变误差模型对观测场景SAR 图像进行天线方向图校正,结果表明,根据滑动聚束SAR 天线方向图二维空变特性建立二维多项式模型来进行校正的方法可以有效降低天线方向图二维空变误差的影响,大大提高滑动聚束SAR辐射定标精度。

1 滑动聚束SAR 信号模型

滑动聚束SAR 通过控制辐照区在地面移动的速度来增加方位向相干累积的时间,从而提高了SAR 方位向的分辨率。 滑动聚束SAR 的成像工作模式如图1 所示。

图1 滑动聚束SAR 成像工作模式示意图Fig.1 Imaging mode of sliding spotlight SAR

滑动聚束SAR 信号模型可以表示为[9-13]:

由此,滑动聚束SAR 信号模型则可以进一步表示为:

2 天线方向图特性分析

为了对滑动聚束模式下SAR 天线方向图二维空变特性进行分析,仿真了雷达观测场景内不同距离向和方位向的点目标数据,通过分析不同位置点目标天线方向图增益变化得到滑动聚束模式下SAR天线方向图二维空变特性,仿真系统参数如表1 所列。 仿真场景大小为6 km(距离向) × 12 km(方位向),共仿真了7×59 个点目标,分别沿方位向和距离向均匀布设,如图2 所示。

表1 仿真系统参数Tab.1 SAR parameters of simulation

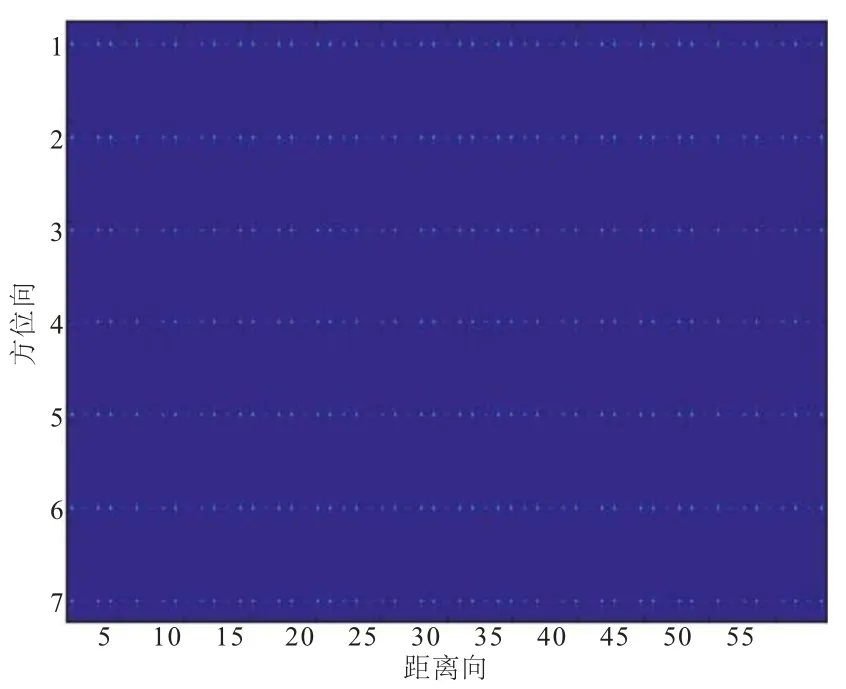
图2 仿真点目标图像Fig.2 Simulation of point targets SAR Image

分别计算同一距离向的不同点目标幅度值即可提取距离向天线方向图,不同方位向位置提取的距离向方向图如图3 所示。

图3 滑动聚束模式天线方向图变化特性示意图Fig.3 Sketch map of 2-D spatially varying antenna gain patterns of sliding spotlight SAR

图3(a)所示为仿真场景1 ~7 行点目标提取的距离向方向图,图3(b)所示为1 ~7 行点目标提取的距离向方向图相对于场景中心第4 行提取方向图的相对变化误差。 由仿真结果可以看出,滑动聚束模式下天线方向图沿距离向呈现Sinc 函数特性变化,而不同于传统条带模式,不同方位向提取的天线方向图也是变化的,因此,滑动聚束模式下天线方向图是二维空变的。 从图3(b)中不同方位向提取天线方向图相对变化可以看出,滑动聚束模式下天线方向图方位向变化特性呈现关于场景中心所在行对称变化,即图像首尾行变化特性相似,且距离图像中心越远,方向图变化越大。

3 天线方向图空变误差校正

根据第2 节中滑动聚束模式下天线方向图二维变化特性仿真分析结果,可以将天线方向图二维空变误差表示为关于场景目标位置的二维多项式函数模型,多项式阶数越高,逼近精度越高,但模型系数也会随之增多,本文结合校正精度和模型系数约束,建立天线方向图校正模型如下:

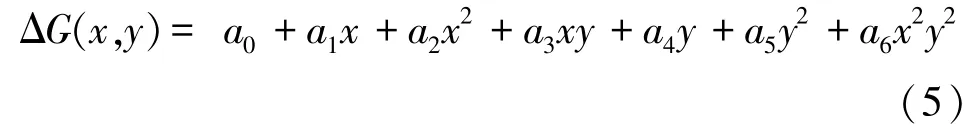
其中,ΔG(x,y)表示滑动聚束模式下天线方向图二维空变误差,(x,y)表示目标点对应图像像素位置,ai表示加权系数。

通过在均匀场景内不同方位向和距离向位置布设标准三角反射器,利用场景中心对应距离向天线方向图对滑动聚束模式SAR 图像进行校正,然后分别提取所有角反射器幅度信息来求解天线方向图二维空变误差模型系数,即

其中,P为n×7 维目标点位置矩阵,A为 7×1 维天线方向图模型系数矩阵,ΔG为n×1 维目标点天线方向图误差矩阵。

由广义逆法即可求得超定线性方程组的最小二乘解[13-15],即天线方向图模型系数矩阵A为

其中,P+为矩阵P的广义逆矩阵。

利用布设的定标器求解出天线方向图二维空变误差模型系数后,可基于误差模型来校正滑动聚束模式SAR 图像,降低天线方向图二维空变特性对SAR 辐射精度的影响,具体流程如图4 所示。

图4 滑动聚束模式天线方向图误差校正流程Fig.4 Schematic of correction method for antenna pattern error of sliding spotlight SAR

4 天线方向图校正结果及分析

为了验证基于天线方向图空变模型的校正方法精度,在图 2 仿真 SAR 图像中第 1、3、7 行分别选取若干个点目标作为参考点来解算天线方向图模型系数,然后利用基于天线方向图空变模型来对SAR 图像进行校正,通过比较校正前后天线方向图误差来评估该校正方法精度和有效性。

4.1 理想情况下校正结果

理想情况下不考虑点目标RCS 一致性及信杂比等因素对参考点目标幅度的影响,那么通过点目标提取的天线方向图空变误差模型校正结果可以评估模型本身引入的误差量。 在仿真SAR 图像中第1、3、7 行分别选取3 个点目标作为参考点,其余所有点目标作为检验点,校正结果如图5 所示。

图5 理想情况下天线方向图误差校正结果Fig.5 Correction result of antenna pattern error in ideal condition

由图5 结果可以看出,理想情况下基于天线方向图空变模型的校正方法精度很高,模型本身引入的误差量小于0.05 dB,因而基于天线方向图空变模型的校正方法理论上是完全可行的。

4.2 误差影响下校正结果

为了评估考虑点目标RCS 一致性及信杂比等误差因素影响下天线方向图校正精度,假设参考点目标幅度一致性误差为均值为0,标准差为0.2 dB高斯分布时,分别选取第1、3、7 行若干点目标作为参考点,进行500 次蒙特卡罗仿真实验,结果如图6及表2 所示。

图6 每行选取9 个点天线方向图误差校正结果Fig.6 Correction result of antenna pattern error by 9 point targets each row

表2 不同参考目标点下天线方向图误差校正结果Tab.2 Correction results of antenna pattern error by choosing different point targets each row

图6 所示为第1、3、7 行每行选取9 个参考目标点,进行500 次蒙特卡罗实验统计仿真场景内所有目标点天线方向图校正RMS 误差,由图中结果可以看出,校正后仿真场景内天线方向图RMS 误差小于0.17 dB。 表2 所示为选取不同参考点个数时天线方向图校正误差结果,可以看出随着参考点数增加,天线方向图校正误差逐渐减小,主要由于多参考点可以抑制参考点目标幅度随机误差的影响。

通过误差影响下基于天线方向图空变模型的滑动聚束模式下天线方向图校正结果可以看出,该校正方法可以有效地校正天线方向图二维空变误差,从而提高SAR 系统辐射测量精度。 校正时只需要在定标场一次获取校正模型参数,对于无控制点区域图像,可以利用定标场获取的校正模型对不同位置图像进行校正,即可实现滑动聚束SAR 二维空变天线方向图误差校正,具有很强的实用性。

4 结论

滑动聚束SAR 通过控制天线波束扫描来提高SAR 系统方位向分辨率,但这种波束指向的不断变化导致SAR 天线方向图对于观测区域目标的加权在距离向和方位向是二维空变的,这种二维空变特性导致采用传统SAR 天线方向图测量和校正方法会引入较大误差。 本文基于滑动聚束SAR 仿真数据对滑动聚束模式下SAR 天线方向图二维空变特性进行了分析,并建立距离向和方位向二维多项式模型来校正SAR 天线方向图二维空变误差,仿真实验结果表明,本方法可以有效降低天线方向图二维空变误差的影响,大大提高滑动聚束SAR 数据产品质量,为后续开展定量化应用奠定基础。