初应力对LiNbO 基底声表面波波速的影响①3
2021-02-23李向阳孙雪平张学娇郭明明魏金金
李向阳, 孙雪平,张学娇, 陈 祥,刘 政,郭明明,魏金金
(1.中国空间技术研究院西安分院,西安 710000;2.西安工业大学, 西安 710126)
0 引言
声表面波(surface acoustic wave,SAW)技术是20 世纪60 年代发展起来的一门技术,它是声学和电子学相结合的一门边缘学科。 由于SAW 器件具有体积小、重量轻以及易加工性等优点被广泛的应用于滤波和传感等领域。 例如,SAW 滤波技术在当前的5G 通信领域仍有很大的发展潜力。 然而,SAW器件在生产和使用的过程中,由于环境和加工方面的原因不可避免的存在初应力、初应变以及残留应力等偏场。 为了更加精确的设计SAW 器件,需要将这些偏场(如初始应力和应变)考虑在内。 然而偏场的存在将会导致线性压电理论的失效[1]。 目前,考虑偏场作用下SAW 的传播行为可以分为两种方法:初始应力理论和偏场方法。
初始应力理论是可以从偏场方法得出的。 一般情况下,初始应力理论是自由能仅取展开式的前三项的偏场方法的结果,即不考虑三阶及三阶以上的材料常数[1-2]。 利用初始应力理论,Gangul 研究了在初应力作用下,Bleustein-Gulyaev 波在压电介质半空间中的传播[3]。 刘华等人研究了层合结构中Rayleigh 波、Lamb 波和 Love 波的传播特性[4-6]。 Du等讨论了在初始应力下磁电弹性层合结构中Love和SH 波的传播[7]。 Singh 研究了在旋转初始应力下Rayleigh 波在压电介质半空间中的传播[8]。
Sinha 等分析了石英晶体中温度对SAW 速度的影响[9]。 Yang 采用偏场方法研究了在初应力作用下Bleustein-Gulyaev 波在压电介质半空间中的传播[10],但是由于缺少三阶材料常数并未给出实例。Simionescu-Panait 分析了初始偏场作用下衰减波和SH 波的传播特性[11],考虑了在初始场作用下弹性常数的变化,但在其文章中忽略了三阶材料常数的影响。
另外,各向异性的压电晶体的三阶材料常数的获取是一个非常复杂的任务,需要首先计算出独立的材料常数分量个数,然后选取合适的独立分量进行试验,进而获取全部的材料常数。
本文严格按照偏场方法分析了初始应力对SAW 传播速度的影响。 利用偏场方法获得了电弹性波动方程。 根据初始应力求解了初始应变和初始电场,并在文献[12]的基础上计算了所有的三阶材料常数。 将这些初始应变、初始电场和二阶、三阶材料常数带入电弹性波动方程,获得了相速度随着初始应力变化的关系。 同时计算了只考虑初始应力的影响下即初始应力理论的相速度变化曲线。 通过对比发现,三阶弹性常数和在初始应力下产生的偏场对相速度的影响很大。
1 偏载下的波动方程
压电介质在外界应力、电场等静态偏载作用下会产生一定的预变形,研究预变形介质中的波动问题属于有限变形过程,将电弹性体变形过程划分为三个阶段[13],如图1 所示。
1)参考状态或自然状态:物体没有发生变形且不受电场、应力作用时的起始状态。 参考状态下的物质点用X表示,其分量为XK。
2)初始状态:此时,物体受到了应力或者电场,并且发生了有限静态变形。 此时,物质点X的位置为x=x(X)或xγ=xγ(X),与参考状态物质点XK的关系为xγ=δγK(XK+wK),wK为初始位移增量。
3)现时状态:在已在初始状态下发生静态变形的基础上再加上与事件相关的小增量变形和电场。物质点X的最终位置为yi=yi(X,t),与初始状态物质点xγ的关系为yi=δiγ(xγ+uγ)。
在2)中的δγK为转移张量,表示参考坐标系和初始状态中的坐标系的坐标轴夹角的方向余弦,起着联系两个坐标系分量的作用;同样的,δiγ为初始状态中的坐标系和现时状态下的坐标系的转移张量。 这样的约定规定了空间坐标的微分形式,形式如式(1)
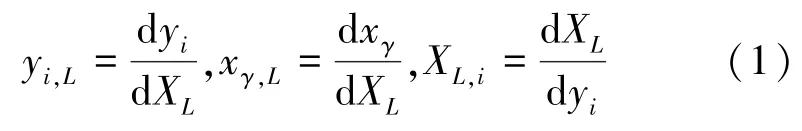

δij(下标在同一个坐标系的符号)为Kronecker 记号。
根据参考文献[12,13],非线性电弹性理论的运动方程和电荷平衡方程为:

式(3)中,ρ0为参考构形下质量密度,fi为现时状态下单位质量的体力,ρE为参考状态下的自由电荷体密度。KLi为第一类piola-kirchhoff 应力张量,可表示为:

DK为参考电位移矢量,

在式(4)中,χ为电性吉布斯自由能密度函数,SKL为应变张量,EK为参考电场:
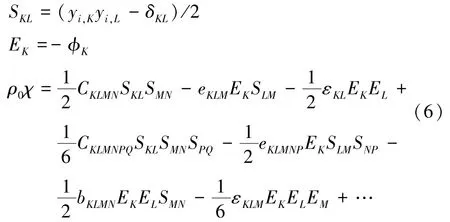
在式(6)中,CKLMN,eKLM,εKL分别为二阶弹性常数、压电常数和介电常数;CKLMNPQ,eKLMNP,bKLMN,εKLM分别为三阶弹性常数、压电常数、电致伸缩系数和介电常数。
同理,可以得到在初始状态下的运动方程和电荷平衡方程:

则可以得到化简后的第一类应力张KLi和电位移矢量Dk,可表示为[14]:
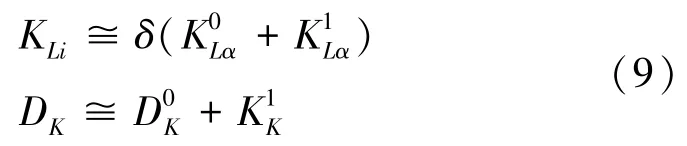
再假设单位质量的体力和单位质量的电荷密度可表达为:

由式(3)(7)(8)(9)(10),可以得到迭加在有限偏场上的小增量场的线性基本方程为:

在式(12)中,GLαMγ,RMLα,LKL分别为有效弹性常数,有效压电常数和有效介电常数,其表达式分别为:

从式(13)关于有效材料常数的表达式中可以看到,有效材料常数和偏载应变、偏载电场和偏载应力有关。 对于非均匀偏载,偏载随着空间的变化而变化,因此有效材料常数也会随着空间位置而发生变化。 对于均匀偏载,有效材料常数比较一致不会随着空间位置而变化。 通过比较材料常数,会发现有效弹性常数和有效介电常数具有对称性:

本文中,考虑的偏场(偏应力)比较小,忽略两次以上的初始偏载场( 如),通过化简,可以得到相对简单的有效材料常数的表达式:

为更方便的研究,设参考坐标系和初始坐标系采用同一个坐标系,如图1 所示,这样转移张量就变为Kronecker 张量。 将下标希腊字母变为大写字母,从参考状态到初始状态变形的位移梯度wγ,K变为
本文选择各向同性刚体旋转从而在计算的过程中忽略了旋转张量[15]ωKL。
假设不存在体力和体电荷,将式(12)带入式(11),并考虑式(8),得到
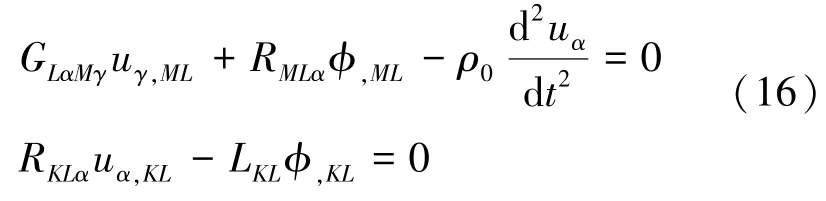
2 3m 晶系独立三阶独立常数的确定
在式(15)中,了解到有效材料常数不仅需要二阶材料常数还需要三阶材料常数。 由晶体学的理论,根据晶体的对称性进行坐标变换(对称变换)时,不仅晶体物理性质本身保持不变,而且对称变换前后的对应分量也保持不变,也就是变换前后的张量相等。
关于LiNbO3二阶弹性常数、压电常数和介电常数已经在很多论文给出。 而LiNbO3的三阶材料常数由于数量繁多,却很少给出表达。 三阶弹性常数、压电常数、电致伸缩常数和介电常数分别表示为:cijklmn、eiklmn、lijkl、εijk,分别有 36、35、34、33个分量。 因为晶体的对称性,将变换前后的常数根据Voigt 标记法之后,可表达为:cIJK、eiJK、lIJ、εiJ,且有:

二阶弹性常数

其中,小写字母取值为1,2,3,大写字母取值为1,2,3,4,5,6,这样三阶弹性常数的分量减少为56个,三阶压电常数减少为63 个,三阶电致伸缩常数减少为36 个,三阶介电常数减少为18 个。
针对3m 点群的晶体,x=0 的面是对称面,z 轴为三阶转轴,根据Neumann 原则,晶体的弹性常数、压电常数、电致伸缩常数和介电常数经过上述对称性操作,其值不应改变。 在进行变换时,不采用Voigt 标记法,只是在变换前和变换后采用Voigt 方便的表达。 设坐标变换矩阵为aij,则

1)对于x=0 的对称面,它的坐标变换矩阵为:

通过此变换可以得到:

2)z轴为三阶转轴,其坐标变换矩阵为:

按照式(19)提供的变换矩阵,对三阶弹性常数进行式(17)的变换,可以得到18 个表达式,所以对于三阶弹性常数有14 个独立分量,根据文献[12]提供的三阶独立常数,本文亦选取这些独立分量:c111、c112、c113、c114、c123、c124、c133、c134、c144、c155、c222、c333、c344、c444,可求取其他分量表达,见附录2。 同理,可以对三阶压电常数、电致伸缩常数和介电常数进行变换,分别得到 21、12、6 个表达式,分别有 13 个、8 个、4个独立分量。 再分别选取独立分量:e115、e116、e125、e126、e135、e136、e145、e311、e312、e313、e314、e333、e344,l11、l12、l13、l14、l31、l33、l41、l44,ε15、ε22、ε31、ε33,其他分量表达亦见附录2。 但是在文献[12]中,三阶介电常数只给出了三个独立分量, 无法通过这三个分量求出,因此本文的计算过程中认为ε15=ε24=0。

介电常数
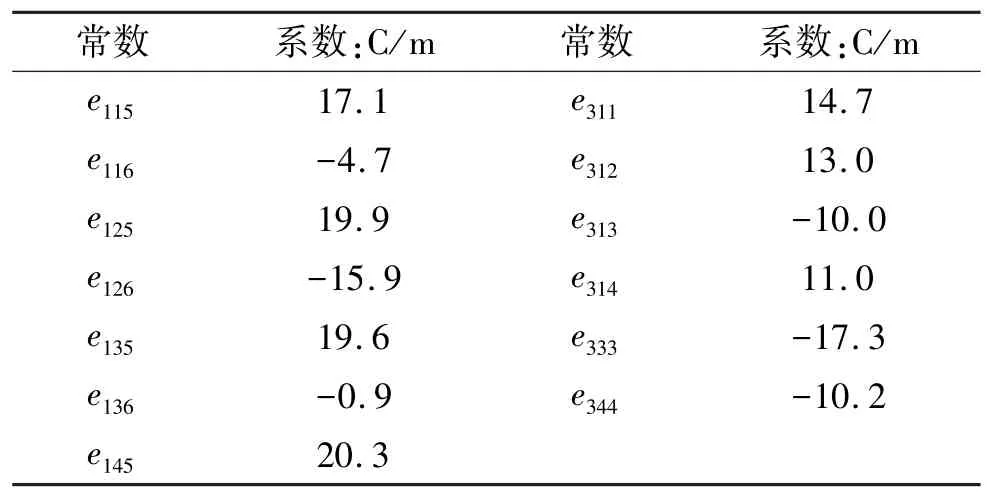
三阶压电常数
3 表面无应力条件下波动方程的求解
压电材料的边界条件包含了力学边界条件和电学边界条件[16]。 力学边界条件包括了应力边界条件和位移边界条件。 应力边界条件为:


因为边界位移是变化的,是未知量,因此不能给出位移边界条件。
电学边界条件也包含了表面电势和边界电位移:

为在参考构形下单位面积上的电荷增量,对于压电材料单位面积上的电荷增量同样为0。
在自由空间中的电位移可表达为

在满足边界条件式(24)的情况下,求解偏载条件下的耦合波动方程式(16)和传统的处理未加偏载的情况类似。 只是由于材料常数对称性发生了改变,在求解算法上稍有不同。 仍采用图2 所示的坐标系,X1 为SAW 的传播方向,X3 为基片表面的外法线方向。

图2 半无限大压电介质坐标示意图Fig.2 Coordinate diagram of half space piezoelectric mediu
设波动方程式(16)具有如下形式的分波解:

式(25)中k为沿X1方向的波数,设沿X3方向的衰减因子为β,不考虑X2方向,X1方向无衰减,则有
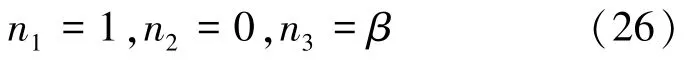
将式(25)和(26)带入到式(16),并写成矩阵形式有:

式中的矩阵元分别为:
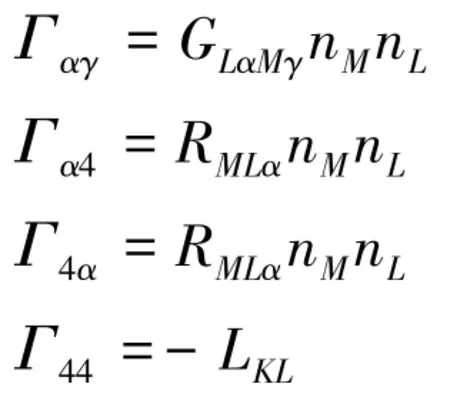
式中下标取值为M,L,α,γ=1,2,3。
一般情况下,式(27)是一个关于待定衰减因子β的八次方程,按照选根原则[17]选取其中四个合适的根。 而耦合波动方程的解还必须要满足半无限压电介质表面的边界条件,所以其一般解应为选取的四个根所对应的四组基本解的线性组合,即:

式(28)中Cn为加权系数,其中C4=1,其余由边界条件定出。
将式(28)代入边界条件式(24),可以得到

将式(29)写成矩阵的形式:
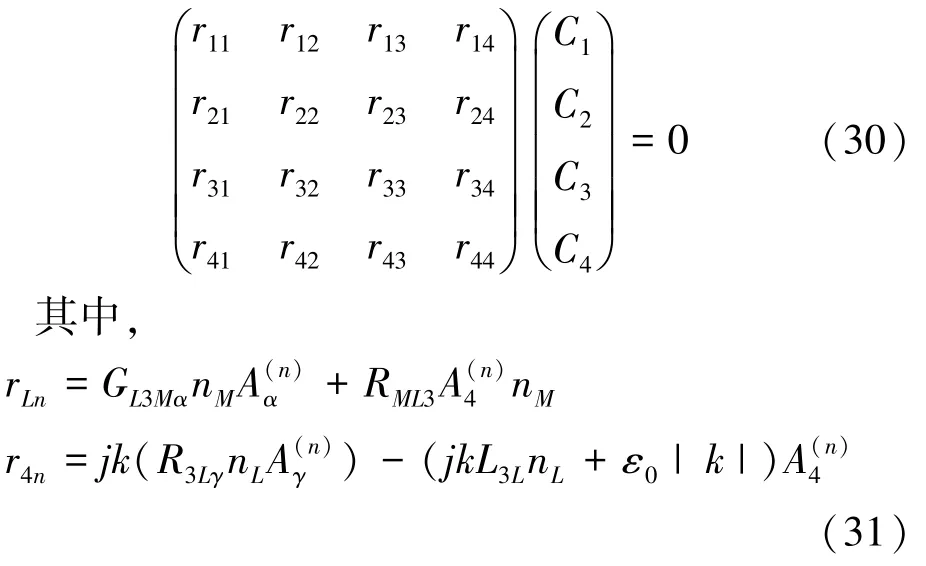
一般情况下,联立方程式(27)和式(30),原则上可以求出SAW 的速度和衰减因子。 然而对各向异性压电介质,求解是非常困难的,按照文献[18-20]给出的方法进行计算。
4 数值计算和分析
YX LINbO3的二阶和三阶材料参数:弹性常数,压电系数,介电系数以及电致伸缩系数在附录中已给出[12,21]。 根据压电介质的本构关系求出在初始应力下的初始应变和初始电场。 本构关系可表示为式(32):

电致伸缩系数

式(32)中σij,Sij,Dm,Em分别为应力、应变、电位移和电场分量。
将LiNbO3的二阶和三阶常数,初始应力,初始应变和初始电场以及基础材料常数带入有效材料常数的表达式中,求出有效材料常数。 本文中的初始应力是均匀的,并且较小,所以求出的有效材料常数在给定的初始应力下是常数[22-23]。 再根据第三节中的求解过程,从而求出了在初始应力下的相速度,并画出了初始应力和相速度的关系曲线,如图3 所示,初应力对 LiNbO3中传播的相速度有明显的影响;在-1 000 ~1 000 MPa 范围内,相速度和初应力的变化关系都不同。 相速度随着初应力的增大而先快速增大,当初应力增加到270 MPa 时相速度达到最大3 852 m/s,且在270 ~400 MPa 之间相速度基本保持不变,而后相速度会逐渐减小。 然而,相速度随着的增大先缓慢增大,在增大到-540 MPa时,相速度增加到最大 3 871 m/s, 在-540 ~-440 MPa 之间相速度基本保持在3 871 m/s,随后会随着初应力的增加而快速下降。 相速度和初应力的变化关系与前两者有很大的区别,相速度随着初应力的增加而线性的减小,变化速率为MPa/m/s, 三者在无初应力时交与相速度3 830 m/s。

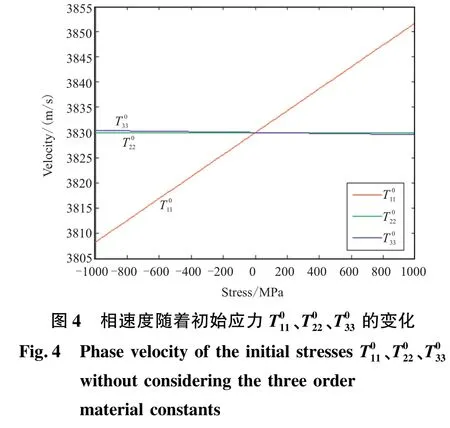
为了说明初应力对相速度的影响中,三阶弹性常数和初应力产生的其他初始偏场的影响也很大,本文根据初始应力理论也得到了相速度随着初始应力的变化关系,如图4 所示,仅有初应力会明显的影响相速度的变化,随着初应力的增加,相速度线性的增加,变化率为MPa/m/s;相速度在初应力从-1 000 ~1 000 MPa 的变化范围内仅变化了0.8 m/s,而在的影响下,相速度不变。
5 结论
通过对比图3 和图4,知道了三阶弹性常数和初应力产生的其他偏场对相速度的影响很大。 为了更精确考虑初应力对相速度的影响,需要采用比初应力理论更严格的理论——偏场方法,即本文中所采取的方法。

三阶弹性常数
在设计高频SAW 器件时需要高的声速,本文就提供了一种提高声速的方法,如在传播方向提供拉应力=270 ~400 MPa,又如在垂直于传播面的方向提供压应力=440 ~540 MPa,从而为设计者设计SAW 器件提供指导。
附录1

二阶压电常数
附录2
三阶弹性常数关系

三阶压电常数关系

电致伸缩系数关系
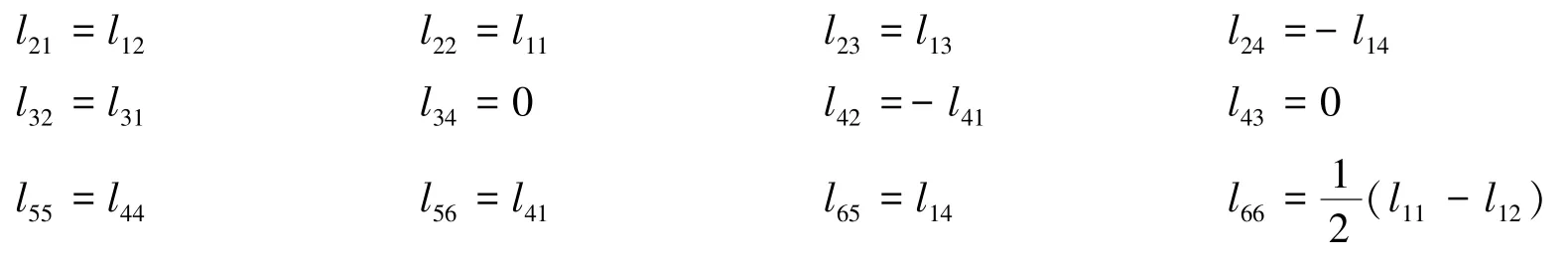
电致伸缩系数关系

