丢番图方程x2+(2n)2=y9(1≤n≤7)的整数解
2021-02-23陈一维柴向阳
陈一维, 柴向阳
(华北水利水电大学 数学与统计学院,郑州 450045)
0 引 言
设B∈N,研究指数型 Lebesgue-Nagell 不定方程:
x2+B=yk
(1)
的整数解是数论中的一类重要课题,已经有了不少研究成果[1-10]。在B=(2n)2,k=9时,式(1) 的整数解问题研究中,李伟[11]证明了n=1时,不定方程x2+4=y9无整数解;杨全[12]证明了n=2时,不定方程x2+16=y9无整数解;许宏鑫等[13]在求解不定方程x2+4k=y9的整数解时,证明了n=4时,不定方程x2+64=y9无整数解,n=8时x2+256=y9仅有整数解 (x,y)=(±16,4)。但对于n=3和n≥5的情况还并未有过讨论。本文在此基础上,就n=3,5,6,7的情况进行了讨论,并给出了不定方程x2+(2n)2=y9在n=3,5,6,7 时无整数解的证明和结论。
1 基本概念及相关性质
引理1 设M是唯一分解整环,正整数k≥2,α,β∈M,(α,β)=1,若αβ=γk,γ∈M,则有α=ε1μk,β=ε2νk,μ,ν∈M,其中ε1,ε2是M中的单位元素,并且ε1ε2=εk,ε为单位元素。
引理2n=1时,x2+4=y9无整数解。
引理3n=2时,x2+16=y9无整数解。
引理4n=4时,x2+64=y9无整数解。
2 定理及其证明
定理1n=3时,不定方程
x2+36=y9(x,y∈Z)
(2)
无整数解。
证明分x≡1(mod 2)和x≡0(mod 2)两种情况进行讨论。
(1)x≡1(mod 2),在Z[i]中,式(2)可以写为(x+6i)(x-6i)=y9,x,y∈Z。
设δ=(x+6i)(x-6i),由δ|(2x,12i)=2得δ只能取1,1+i,2。因x≡1(mod 2),有(x+6i)=1(mod 2),所以δ≠2;若δ=1+i,则N(1+i)|N(x+6i),即2|(x2+36),与x≡1(mod 2)矛盾,所以δ=1。
由引理1,有
x+6i=(a+bi)9,x,a,b∈Z
因此得
x=a9-36a7b2+126a5b4-84a3b6+9ab8
6=b(9a8-84a6b2+126a4b4-36a2b6+b8)
(3)
则b=±1,±2,±3,±6。
b=1时,由式(3)可得
5=3(3a8-28a6b2+42a4b4-12a2b6)
(4)
要使式(4)成立,需要满足3|5,显然不可能,所以b≠1。
b=-1时,由式(3)可得
-7=3(3a8-28a6b2+42a4b4-12a2b6)
(5)
要使式(5)成立,需要满足3|-7,显然不可能,所以b≠-1。
b=2时,由式(3)可得
-253=3(3a8-28a6b2+42a4b4-12a2b6)
(6)
要使式(6)成立,需要满足3|-253,显然不可能,所以b≠2。
b=-2时,由式(3)可得
-259=3(3a8-28a6b2+42a4b4-12a2b6)
(7)
要使式(7)成立,需要满足3|-259,因为a∈Z,所以b≠-2。
b=3时,由式(3)可得
-6 559=3(3a8-28a6b2+42a4b4-12a2b6)
(8)
要使式(8)成立,需要满足3|-6 559,因为a∈Z,所以b≠3。
b=-3时,由式(3)可得
-6 563=3(3a8-28a6b2+42a4b4-12a2b6)
(9)
要使式(9)成立,需要满足3|-6 563,因为a∈Z,所以b≠-3。
b=6时,由式(3)可得
-1 679 617=3(3a8-28a6b2+42a4b4-12a2b6)
(10)
要使式(10)成立,需要满足3|-1 679 615,因为a∈Z,所以b≠6。
b=-6时,由式(3)可得
-1 679 617=3(3a8-28a6b2+42a4b4-12a2b6)
(11)
要使式(11)成立,需要满足3|-1 679 617,因为a∈Z,所以b≠-6。
所以当x=1(mod 2),n=3时,不定方程x2+36=y9(x,y∈Z)无整数解。
(2)x≡0(mod 2)时。可知x为偶数,则y=0(mod 2)。设x=2x1,y=2y1,代入式(2)得
设x1=2x2+1,得
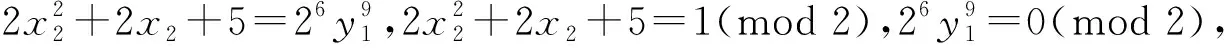
故n=3时,不定方程x2+(2n)2=y9无整数解。
定理2n=5时,不定方程
x2+100=y9(x,y∈Z)
(12)
无整数解。
证明分x≡1(mod 2)和x≡0(mod 2)两种情况进行讨论。
(1) 当x≡1(mod 2)时,在Z[i]中,式(12)可以写为(x+10i)(x-10i)=y9,x,y∈Z。
设δ=(x+10i)(x-10i),由δ|(2x,20i)=2得δ只能取1,1+i,2。因x≡1(mod 2),有(x+10i)=1(mod 2),所以δ≠2;若δ=1+i,则N(1+i)|N(x+6i),即2|(x2+100),与x≡1(mod 2)矛盾,所以δ=1。
由此和引理1,有
x+10i=(a+bi)9,x,a,b∈Z
因此得
x=a9-36a7b2+126a5b4-84a3b6+9ab8
10=b(9a8-84a6b2+126a4b4-36a2b6+b8)
(13)
则b=±1,±2,±5,±10。
b=1时,由式(13)可得
9=a2(9a6-84a4b2+126a2b4-36b6)
(14)
要使式(14)成立,则a2=1或a2=9。
a2=1,b=1代入式(14)可得
a2(9a6-84a4b2+126a2b4-36b6)=15≠9
a2=9,b=1代入式(14)可得
a2(9a6-84a4b2+126a2b4-36b6)=7695≠9
所以b≠1。
b=-1时,由式(13)可得
-11=3(3a8-28a6b2+42a4b4-12a2b6)
(15)
要使式(15)成立,需要满足3|-11,显然不可能,所以b≠-1。
b=2时,由式(13)得
-251=3(3a8-28a6b2+42a4b4-12a2b6)
(16)
要使式(16)成立,需要满足3|-251,因为a∈Z,所以b≠2。
b=-2时,由式(13)可得
-261=a2(9a6-84a4b2+126a2b4-36b6)
(17)
要使式(17)成立,则a2=1或a2=9。
将a2=1,b=-2代入式(17)可得
a2(9a6-84a4b2+126a2b4-36b6)=
-615≠-261
将a2=1,b=-2代入式(17)可得
a2(9a6-84a4b2+126a2b4-36b6)=
-43 335≠-261
所以b≠-2。
b=5时,由式(13)可得
-390 623=3(3a8-28a6b2+42a4b4-12a2b6)
(18)
要使式(18)成立,需要满足3|-390 623,因为a∈Z,所以b≠5。
b=-5时,由式(13)可得
-390 627=a2(9a6-84a4b2+126a2b4-36b6)
(19)
-3×3×43 403=a2(9a6-84a4b2+126a2b4-36b6)
要使式(19)成立,则a2=1或a2=9。
a2=1,b=-5代入式(19)可得
a2(9a6b-84a4b2+126a2b4-36b6)=
-485 841≠-390 627
a2=9,b=-5代入式(19)可得
a2(9a6b-84a4b2+126a2b4-36b6)=
-155 601≠-390 627
所以b≠-5。
b=10时,由式(13)可得
1-108=a2(9a6-84a4b2+126a2b4-36b6)
也即
-99 999 999=a2(9a6-84a4b2+126a2b4-36b6)
(20)
-3×3×11 111 111=a2(9a6-84a4b2+126a2b4-36b6)
要使式(20)成立,则a2=1或a2=9,将a2=1,b=10 代入式(20)可得
a2(9a6-84a4b2+126a2b4-36b6)=
-34 748 391≠-99 999 999
a2=9,b=10代入式(20)可得
a2(9a6-84a4b2+126a2b4-36b6)=
-228 004 551≠-99 999 999
所以b≠10。
b=-10时,由式(13)可得
-100 000 001=
3(3a8-28a6b2+42a4b4-12a2b6)
(21)
要使式(21)成立,需要满足3|-100 000 001,因为a∈Z,所以b≠-10。
所以当x=1(mod 2),n=5时,不定方程x2+100=y9无整数解。
(2)x≡0(mod 2)时,可知x为偶数,则y=0(mod 2)。设x=2x1,y=2y1,代入式(12)可得
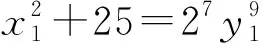
设x1=2x2+1,得

故n=5时不定方程x2+(2n)2=y9无整数解。
定理3
n=6时,不定方程
x2+144=y9(x,y∈Z)
(22)
无整数解。
证明分x≡1(mod 2)和x≡0(mod 2)两种情况进行讨论。
(1) 当x≡1(mod 2)时,在Z[i] 中,式(2)可以写为(x+12i)(x-12i)=y9,x,y∈Z。
设δ=(x+12i)(x-12i),由δ|(2x,24i)=2得δ只能取1,1+i,2。因x≡1(mod 2),有(x+12i)=1(mod 2),所以δ≠2;若δ=1+i,则N(1+i)|N(x+12i),即2|(x2+144),与x≡1(mod 2)矛盾,所以δ=1。
由此和引理1,有
x+12i=(a+bi)9,x,a,b∈Z
因此有
x=a9-36a7b2+126a5b4-84a3b6+9ab8
12=b(9a8-84a6b2+126a4b4-36a2b6+b8)
(23)
则b=±1,±2,±3,±4,±6,±12。
b=1时,由式(23)可得
11=3(3a8-28a6b2+42a4b4-12a2b6)
(24)
要使式(24)成立,需要满足3|11,显然不可能,所以b≠1。
b=-1时,由式(23)可得
-13=3(3a8-28a6b2+42a4b4-12a2b6)
(25)
要使式(25)成立,需要满足3|-13,显然不可能,所以b≠-1。
b=2时,由式(23)可得
-250=3(3a8-28a6b2+42a4b4-12a2b6)
(26)
要使式(26)成立,需要满足3|-250,因为a∈Z,所以b≠2。
b=-2时,由式(23)得
-262=3(3a8-28a6b2+42a4b4-12a2b6)
(27)
要使式(27)成立,需要满足,因为a∈Z,所以b≠-2。
b=3时,由式(23)得
-6 557=3(3a8-28a6b2+42a4b4-12a2b6)
(28)
要使式(28)成立,需要满足3|-6 557,因为a∈Z,所以b≠3。
b=-3时,由式(23)得
-6 565=3(3a8-28a6b2+42a4b4-12a2b6)
(29)
要使式(29)成立,需要满足3|-6 565,因为a∈Z,所以b≠-3。
b=4时,由式(23)可得
3-48=a2(9a6-84a4b2+126a2b4-36b6)
也即
-65 533=a2(9a6-84a4b2+126a2b4-36b6)
(30)
-3×3×3×3×8 093=a2(9a6-84a4b2+126a2b4-36b6)
要使式(30)成立,则a2=1或a2=9,或a2=81。
a2=1,b=4代入式(30)可得
a2(9a6-84a4b2+126a2b4-36b6)=-116 535≠-65 533
a2=9,b=4代入式(30)可得
a2(9a6-84a4b2+126a2b4-36b6)=
-364 905≠-65 533
a2=81,b=4代入式(30)可得
a2(9a6-84a4b2+126a2b4-36b6)=
-127 148 535≠-65 533
所以b≠4。
b=-4时,由式(23)可得
-65 539=3(3a8-28a6b2+42a4b4-12a2b6)
(31)
要使式(31)成立,需要满足3|65 539,因为a∈Z,所以b≠-4。
b=6时,由式(23)可得
2-68=3(3a8-28a6b2+42a4b4-12a2b6)
也即
-1 679 614=3(3a8-28a6b2+42a4b4-12a2b6)
(32)
要使式(32)成立,需要满足3|-1 679 614,因为a∈Z,所以b≠6。
b=-6时,由式(23)可得
-2-68=3(3a8-28a6b2+42a4b4-12a2b6)
也即
-1 679 618=3(3a8-28a6b2+42a4b4-12a2b6)
(33)
要使式(33)成立,需要满足3|-1 679 618,因为a∈Z,所以b≠-6。
b=12时,由式(23)可得
1-128=3(3a8-28a6b2+42a4b4-12a2b6)
也即
-429 981 695=3(3a8-28a6b2+42a4b4-12a2b6)
(34)
要使式(34)成立,需要满足3|-42 981 695,因为a∈Z,所以b≠12。
b=-12时,由式(23)可得
-1-128=3(3a8-28a6b2+42a4b4-12a2b6)
也即
-429 981 697=3(3a8-28a6b2+42a4b4-12a2b6)
(35)
要使式(35)成立,需要满足3|-429 981 697,因为a∈Z,所以b≠-12。
所以当x=1(mod 2),n=5时,不定方程x2+144=y9无整数解。
(2)x≡0(mod 2)时,可知x为偶数,则y=0(mod 2)。设x=2x1,y=2y1,代入式(22)可得

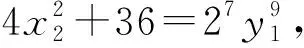

故n=6时,不定方程x2+(2n)2=y9无整数解。
定理4
n=7时,不定方程
x2+196=y9(x,y∈Z)
(36)
无整数解。
证明分x≡1(mod 2)和x≡0(mod 2)两种情况进行讨论。
(1) 当x≡1(mod 2)时,在Z[i]中,(2)式可以写为(x+7i)(x-7i)=y9,x,y∈Z。
设δ=(x+7i)(x-7i),由δ|(2x,14i)=2得δ只能取1,1+i,2。因x≡1(mod 2),有(x+7i)=1(mod 2),所以δ≠2;若δ=1+i,则N(1+i)|N(x+7i),即2|(x2+196),与x≡1(mod2)矛盾,所以δ=1。
由此和引理1,有
x+7i=(a+bi)9,x,a,b∈Z
因此有
x=a9-36a7b2+126a5b4-84a3b6+9ab8
14=b(9a8-84a6b2+126a4b4-36a2b6+b8)
(37)
则b=±1,±2,±7,±14。
b=1时,由式(37)得
13=3(3a8-28a6b2+42a4b4-12a2b6)
(38)
要使式(38)成立,需要满足3|13,显然不可能,所以b≠1。
b=-1时,由式(37)得
-15=a2(9a6-84a4b2+126a2b4-36b6)
(39)
要使式(39)成立,则a2=1。
a2=1,b=-1代入式(39)得
a2(9a6-84a4b2+126a2b4-36b6)=15≠-15
所以b≠-1。
b=2时,由式(37)得
-249=a2(9a6-84a4b2+126a2b4-36b6)
(40)
也即
-3×83=a2(9a6-84a4b2+126a2b4-36b6)
要使式(40)成立,则a2=1。
a2=1,b=2代入式(40)可得
a2(9a6-84a4b2+126a2b4-36b6)=
-615≠-249
所以b≠2。
b=-2时,由式(37)可得
-7-28=3(3a8-28a6b2+42a4b4-12a2b6)
也即
-263=3(3a8-28a6b2+42a4b4-12a2b6)
(41)
要使式(41)成立,需要满足3|-263,因为b∈Z,所以b≠-2。
b=7时,由式(37)可得
2-78=3(3a8-28a6b2+42a4b4-12a2b6)
也即
-5 764 799=
3(3a8-28a6b2+42a4b4-12a2b6)
(42)
要使式(42)成立,需要满足3|-5 764 799,因为b∈Z,所以b≠7。
b=-7时,由式(37)得
-2-78=3(3a8-28a6b2+42a4b4-12a2b6)
也即
-5 764 803=3(3a8-28a6b2+42a4b4-12a2b6)
(43)
-3×11×11×15 881=a2(9a6-84a4b2+126a2b4-36b6)
要使式(43)成立,则a2=1或a2=11。
a2=1,b=-7代入式(43)可得
a2(9a6-84a4b2+126a2b4-36b6)=
-3 936 945≠-5 764 803
a2=11,b=-7代入式(43)可得
a2(9a6-84a4b2+126a2b4-36b6)=
-15 329 985≠-5 764 803
所以b≠-7。
b=14时,由式(37)可得
1-148=3(3a8-28a6b2+42a4b4-12a2b6)
也即
-1 475 789 055=a2(9a6-84a4b2+126a2b4-36b6)
(44)
-3×5×13×41×197×937=
a2(9a6-84a4b2+126a2b4-36b6)
要使式(44)成立,则a2=1。
a2=1,b=14代入式(44)得
a2(9a6b-84a4b2+126a2b4-36b6)=
-266 239 335≠-1 475 789 055
所以b≠14。
b=-14时,由式(37)可得
-1-148=
3(3a8-28a6b2+42a4b4-12a2b6)
也即
-1 475 789 057=
3(3a8-28a6b2+42a4b4-12a2b6)
(45)
要使式(45)成立,需要满足3|-1 475 789 057,因为a∈Z,所以b≠-14。
所以当x=1(mod 2),n=7时,不定方程x2+196=y9无整数解。
(2)x≡0(mod 2)时,可知x为偶数,则y=0(mod 2)。设x=2x1,y=2y1,代入式(36)可得

设x1=2x2+1,得

故n=7时,不定方程x2+(2n)2=y9无整数解。
综上所述,得出不定方程x2+(2n)2=y9(1≤n≤7,x,y,n∈Z)时,无整数解。
3 结 论
不定方程是数论方面的一个重要问题,在这方面的研究已经很多,上述过程就不定方程x2+(2n)2=y9在n=3,5,6,7时的整数解问题进行讨论,给出这不定方程x2+(2n)2=y9(n=3,5,6,7,x,y,n∈Z)无整数解的结论和证明,并根据已有结论总结出了不定方程x2+(2n)2=y9(1≤n≤7,x,y,n∈Z)无整数解的结论。 今后希望进一步研究n≥8的情况以及其他形式的不定方程的整数解问题.
