一类非线性带延迟项粘弹性方程的初边值问题*

郑雅匀, 杨 晗

(西南交通大学 数学学院，成都 611756)

0 引 言

研究如下带延迟项粘弹性方程的初边值问题：

(1)

(2)

粘弹性方程是由梁方程演变而来的，对于这一类方程的研究已经有一些文献[1-7]。对于带有记忆项和时间延迟项二阶线性方程的初边值问题：

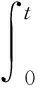
文献[1]应用Galerkin方法，证明了方程弱解的整体存在性和唯一性，并假设在μ1=0时，得到能量衰减的结果；文献[2]则是在μ2<μ1和μ1=μ2两种情况下得到能量衰减的结果；文献[3]在文献[1]的基础上，考虑了非线性源项和非齐次项的情形：

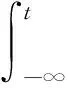
这里f(u)是非线性函数，满足条件：

(3)

其中Cf为正常数，∀u,v∈R+同样应用Galerkin方法，得到方程弱解的整体存在性和唯一性;文献[4-6]则是研究了四阶粘弹性方程情形。值得特别指出的是文献[4]研究了带记忆项、时间延迟项的粘弹性方程的初边值问题:

对于任意实数μ1，μ2，在适当的松弛函数g假设下，应用Galerkin方法，证明了方程弱解的整体存在性和唯一性；文献[6]研究了带有记忆项和时间延迟项的粘弹性方程的初边值问题：

对于任意实数μ1，μ2，且常数α>0 下，对于f(u)满足式(3)，应用Galerkin方法得到弱解的整体存在性和唯一性并适当加强条件得到强解的存在性。

基于以上的分析，文献[1-6]都是研究线性的阻力项，本文将研究非线性的阻力项，讨论带有非线性阻力项，有记忆项、时间延迟项的四阶粘弹性方程，应用Galerkin方法得到整体弱解的存在性和唯一性。

1 主要结论

下面给出本文的主要结论：

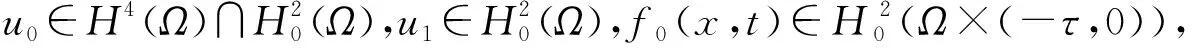
2 准备工作

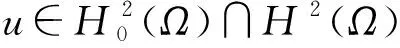
(4)

其中记

(5)

证明由式(4)左端可得:

由式(4)右端并根据式(5)可得:

即等式的左右两端相等，得证。设

下面给出弱解的定义。

定义1 设u∈U是初边值问题的一个弱解，则满足:

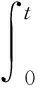
定理1的证明:

证明下用Galerkin方法证明。

步骤1 构造近似解。

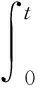
(6)

式(6)满足如下条件:

hjm(t)关于h为多项式形式，则满足局部李普西兹条件，利用微分方程的标准化方法，可以先在一个小区间[0,tm)(00)上对近似系统式(6)(7)求局部解，然后可将这个解通过如下估计延拓至整个区间[0，T]。对于方程中的延迟项，参考文献[1]其给出了详细的证明过程。

步骤2 先验估计。

(8)

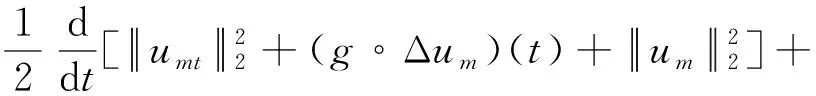
(9)

由函数g(t)满足的条件，则有

根据Cauchy-Schwarz不等式有:

将式(9)在(0,t)上积分有

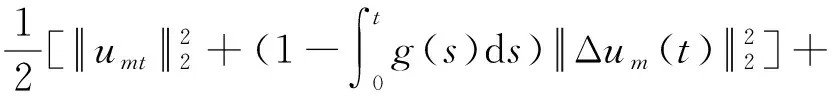
(10)

又当t∈[-τ,0]时,有

(11)

将式(11)代入式(10)有

根据Gronwall不等式和式(7)，对于任意给定T>0,得到:

(12)

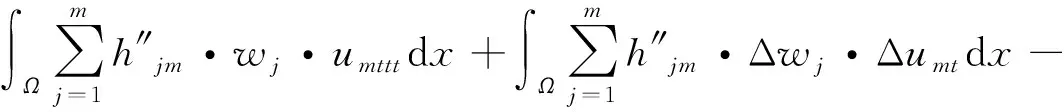
即有

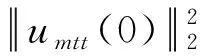
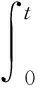
(14)

在式(14)两边同乘以umtt(0)并在Ω上积分,有：

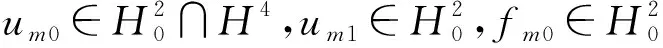
由导数定义,知

则有

(15)

则有

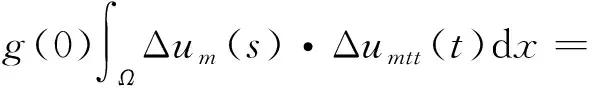
(16)

将式(15)、式(16)代入式(13)得

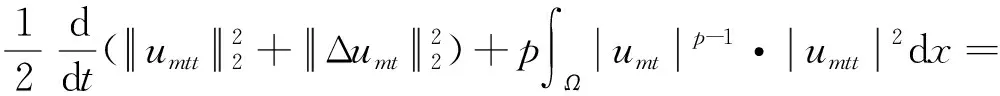
(17)

根据Cauchy-Schwarz不等式、Young不等式和函数g的假设,有

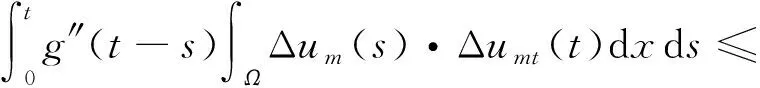
(19)

将式(18)(19)代入式(17),得

(20)

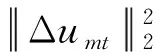
(21)

以下所有η均为常数，根据Cauchy-Schwarz不等式、Young不等式,有

将上述不等式带入式(21)中,有

由第一次估计可知

则有

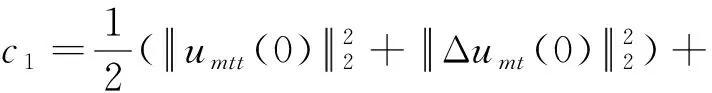
根据Gronwall不等式，对于任意给定T>0,得到

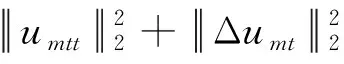
(22)

步骤3 取极限。

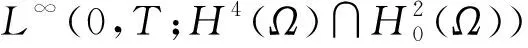
所以对式(6)通过对m求极限得

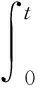
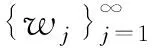
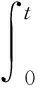
即u是式(1)的整体弱解。

上面证明了问题的存在性，下面证明问题的唯一性。

令u1和u2是问题的两个解，设z=u1-u2，满足：

(23)

且满足:

令式(23)中的v=zt，有

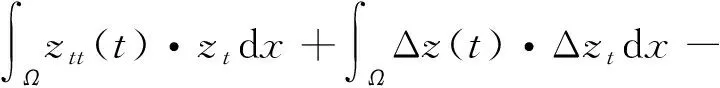
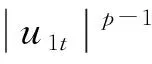
也即

由导数定义，有

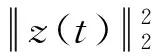
在(0，t)上积分，有

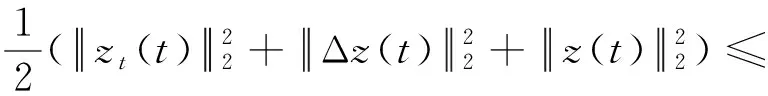
又因为

则有

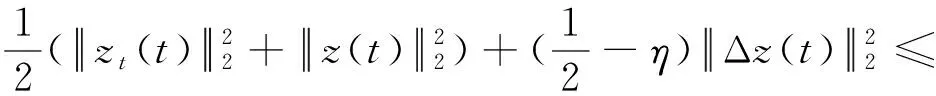
由Gronwall不等式,有

其中

C为正常数。

其唯一性得证。

3 结束语

受文献[4,6]的启发，在对齐次和非齐次情形下的粘弹性方程研究学习中发现，前人研究的均为线性阻力项情况。结合对含有记忆项、时间延迟项的粘弹性方程的研究，想到对带有非线性阻力项的粘弹性方程的初边值问题进行讨论，运用经典的Galerkin方法，通过构造近似解，利用微分标准化方法，先得到局部解再延拓至整个空间，再对近似解进行先验估计，最后取极限，从而得到整体弱解的存在性；再通过假设并验证，最终得到整体弱解的唯一性。对此问题还可进一步研究，对解的性质及衰减性也有一定的研究意义。