两相旋转爆震发动机出口流场均匀性数值研究
2021-02-23孔光明王文鹏张宇坤
马 元,邹 刚,孔光明,孙 静,王文鹏,张宇坤
( 海军航空大学 青岛校区,山东 青岛 266100)
相比于传统的等压燃烧方式,爆震燃烧具有熵增低、自增压以及更高的热循环效率等优点。旋转爆震发动机(Rotating Detonation Engine,RDE)是基于爆震燃烧的一种动力装置,它利用爆震波在环形燃烧室内的一端连续旋转传播,爆震产物从另一端开口处高速排出并产生连续推力。由于RDE没有压气机、涡轮等转动部件,故相比于传统发动机,具有结构简单、研制成本低的特点。此外,RDE还具有大比冲、高推重比、宽工作范围等性能优势,这对于开发新型高效航空航天发动机极具吸引力[1-2]。
近年来,国内外学者采用数值模拟方法对爆震燃烧室的流场特性和爆震旋转机理等进行了探索和研究并取得了一定的进展[3-18]。姜宗林等[3]总结了气相规则胞格爆震波传播与起爆现象的相关研究进展,系统研究了气相规则胞格爆震波起爆和传播统一框架的几个基本要素。滕宏辉等[4]采用数值模拟研究了氢气-空气混合物中二维斜爆震波的起始特性,分析了入口压力和马赫数对起始结构和长度的影响。王兵等[5]总结了有关爆炸、爆震及DDT的研究,讨论了抑制管道内爆炸和爆震的被动/主动或混合方法。谢桥峰等[6]通过实验研究了氢气-空气旋转爆震燃烧室内贫油条件下的燃烧特性,得到了快速爆燃,不稳定爆震、准稳定爆震和稳定爆震等传播模态,并给出了各传播模态的影响因素和特点,对旋转爆震燃烧室的设计和实际应用具有重要指导意义。Yi等[7]研究了喷管形状、扩张角和长度对旋转爆震发动机性能的影响。Schwer等[8-9]首次在数值模拟中将喷注腔与喷注孔考虑在内,对比研究了理想喷注模型与喷孔喷注模型RDE内流场结构及发动机性能的差异,并通过改变微型喷注孔的形状及角度探索燃烧室爆震波对喷注腔压力的影响规律。刘世杰等[10-11]模拟研究了旋转爆震波的详细结构和自持机理,并且发现当发动机尺寸小于临界值时无法成功起爆。姜孝海等[12]采用9组分19步的详细化学反应模型进行数值模拟,模拟结果表明爆震波作用后,受高温膨胀及离心力等作用,产物挤向外壁,形成了一定的密度或压力梯度。邵业涛等[13]采用两步反应模型在矩形计算区域内模拟了爆震波的多个循环过程。马虎等[14-15]基于Fluent软件分析了旋转爆震波的二维结构、入口总压、外界反压和燃烧室长度对RDE性能的影响。周蕊[16-17]通过对喷入流场中的粒子进行追踪,对影响粒子轨迹及其物理参量变化的主要因素进行了分析,得到的RDE热效率约为35.4%,并发现燃烧室半径过大不利于爆震波的稳定传播,波头高度会周期性变化,采用多个波头起爆能够降低或消除大尺寸燃烧室内爆震波不稳定对发动机性能的不利影响。李宝星等[18]通过二维数值模拟研究了进气总压对旋转爆震波的影响,获得了燃烧室内部流场结构和爆震波传播特性,对不同进气总压条件下发动机的爆震性能进行了计算。
早期研究大都针对气态燃料,随着研究的深入,液态燃料的旋转爆震逐渐引起了人们的关注。在实际工程应用中受到重量和空间的限制,应用液态燃料更有优势。与气态燃料相比,液态燃料具有更高的密度比冲,相同体积下具有更高的冲量。郑权等[19]对汽油为燃料,富氧空气为氧化剂的连续旋转爆震发动机进行了试验,得到了不同当量比和不同汽油喷注压力下爆震波的传播特性,其中爆震波传播频率为2.1~2.4 kHz,传播速度为1 022.2~1 171.8 m/s。王迪等[20-21]针对两相连续旋转爆震发动机的喷注器雾化混合、两相爆震起爆与发动机热试车试验情况进行了总结,对俄罗斯、法国、波兰在两相连续旋转爆震发动机有关的试验研究情况进行了论述,对不同构型喷注器工作过程与性能、发动机点火起爆以及不同工质的发动机结构参数及试验情况进行总结与分析。通过试验得到爆震波的时域、频域特征,对两相连续旋转爆震燃烧室中爆震波的起爆过程和稳定后的传播过程进行了研究。马元[22]以汽油为燃料,空气为氧化剂,开展吸气式气液两相RDE的试验研究,分析了当量比、空气喷注总温、空气喷注环缝、喷管等对气液两相旋转爆震波传播的影响。
上述学者的数值研究主要考察了气态燃料下的旋转爆震发动机,国内外对液态燃料旋转爆震发动机数值模拟较少。两相RDE出口流场均匀性对后续加装的涡轮或喷管的设计具有重要的意义,而目前尚未有相关研究发表。本文对以辛烷为燃料、空气为氧化剂的气液两相旋转爆震发动机进行数值模拟,采用DPM模型计算辛烷液滴的轨迹,模拟非预混条件下的旋转爆震波工作过程。对非预混喷注下两相RDE的影响因素进行了研究,得到了空气总温与喷注均匀性对RDE出口流场均匀性的影响,为以后两相RDE的深入研究提供参考。
1 数值方法和物理模型
本文利用商业软件FLUENT,基于密度基求解器求解二维非稳态雷诺时均的N-S控制方程;对流项采用三阶MUSCL格式离散,该格式对激波的捕捉具有较高的精度;物理通量采用AUSM矢通量分裂法进行分解;时间项采用四阶龙格-库塔法;采用标准k-ε湍流模型。以辛烷为燃料,空气为氧化剂,化学反应方程式为C8H18+12.5(O2+3.76N2)→8CO2+9H2O+47N2。DPM模型考虑颗粒的耦合传热/传质,考虑萨夫曼升力和压力梯度力等附加力,考虑液滴的破碎、蒸发等物理过程,射流源采用组射流源。
1.1 模型和边界条件
旋转爆震燃烧室为柱状环型燃烧室,相比于燃烧室的直径,环形厚度相对较小,故将三维环形域简化成二维计算域是合理的。因此为减少计算量节约成本,本文将燃烧室沿母线展开燃烧室内部流场简化成二维矩形计算区域,尺寸为200 mm×50 mm,图1中给出了监测点M1(x=100 mm,y=49 mm)的位置。本文网格尺度为0.5 mm×0.5 mm,为均匀正交网格。

图1 旋转爆震燃烧室二维计算域示意图
本文计算域入口边界的质量通量为100 kg/m2/s,空气总温为300~800 K,见表1所示。计算域的下边界为压力出口边界,分两种情况:当出口为亚音速时,边界点压力等于外界反压,而其他守恒变量由内部流场外推得到,外界反压为0.1 MPa。当出口为超音速时,所有守恒变量由内部区域外推得到。左右边界定义为周期边界,进行数据交换。
辛烷液滴的直径为0.02 mm,初始温度300 K,喷射速度20 m/s,辛烷的射流间距见表2所示,其中Case 15为理想均匀喷注。辛烷的总质量通量为6.667 kg/m2/s,总当量比为1。
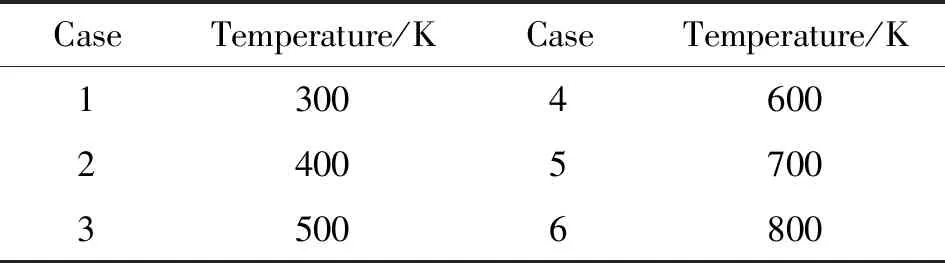
表1 不同空气喷注总温(辛烷射流间距为2 mm)

表2 不同辛烷射流间距(空气喷注总温300 K)
1.2 数值验证
图2(a)为Case 5下爆震波稳定传播时的温度分布云图,其中A是接近入口附近沿周向传播的横向爆震波,B是爆震波头部产生的斜激波,C是滑移线,即新的爆震产物与上一循环的爆震产物形成的接触间断面,D是爆震产物与新鲜反应物的接触面,E是新喷入的新鲜反应物,为旋转爆震的传播提供燃料。图2(b)为 Bykovskii等[23]实验获得的旋转爆震波结构,可以看出数值模拟的燃烧室流场结构与实验结果定性一致。

图2 Case 5的温度云图与Bykovskii实验照片
图3为Case 15监测点M1的压力和温度时程曲线。由图3可知,在爆震波穿过监测点时,压力均呈现急升缓降的特点,每个周期的压力峰值基本保持不变,表明爆震波处于稳定传播状态,且压力曲线与温度曲线吻合较好,表明爆震阵面上激波与化学反应区高度耦合。计算得到平均峰值压力为4.89 MPa,平均峰值温度为 2 898 K,爆震波的平均传播速度为1 649 m/s。与用Chemical Equilibrium with Application(简称CEA)计算得到的爆震波理论C-J压力、C-J温度和C-J速度的相对误差分别为 -5.48%、-0.67%、-8.84%。

图3 监测点M1的压力和温度曲线
1.4 网格无关性验证
在数值方法准确性的基础上,本文对二维RDE流场进行了网格无关性验证。计算域为图4所示二维计算域,网格尺度分别为1.0 mm、0.5 mm和0.25 mm,工况条件为 Case 5。由上节爆震波参数验证表明0.5 mm的网格计算精度可以接受,本文不再对爆震波参数方面的网格无关性进行赘述。

图4 不同网格尺度下燃烧室内温度云图
图4为不同网格尺度下的燃烧室内温度云图,由图4(a)可以看出,在网格尺度1.0 mm下,流场特征非常不明显,如燃烧产物与新鲜反应物的接触断面、滑移线、斜激波等均不稳定,无法满足流场分析的要求。由图4(b)和图4(c)可知,网格尺度0.5 mm和网格尺度0.25 mm下流场特征均非常明显,爆震波、斜激波及接触断面等都很清晰。与 0.5 mm 下的流场相比,0.25 mm下的流场细节特征更加明显,如爆震波后辛烷射流对流场的影响更加清晰,爆震产物与新鲜反应物的接触面及滑移线等更加稳定,但采用DPM模型增加网格量会极大的减缓计算速度,由于本分不考虑流场内特别精细的结构,0.5 mm网格下的流场精度也能满足要求。
综上所述,1.0 mm网格计算精度很差,本文不采用,0.5 mm 网格下的精度和计算速度均能满足要求,0.25 mm网格计算精度最高,但计算速度太慢,受实际计算资源所限,无法满足大量工况的计算,因此本文数值计算均采用0.5 mm的网格。
可见,本文采用的数值方法可行,计算精度可以接受,后续的算例均采用该方法。
2 计算结果与分析
2.1 均匀性评价指标
为表征两相燃烧室某截面的压力分布均匀性,引入相对标准偏差CV,均匀性评价指数γP,克里斯琴森均匀系数CU,现分别介绍这些均匀性评价指标。
CV表征相对变异量的度量,为无量纲值,可以用来衡量均值显著不同的总体离散性,也可用来比较流场均匀性的改善程度:

(1)
(2)
(3)

克里斯琴森均匀系数CU是克里斯琴森1942年提出的,是基于平均偏差的统计量,能够直接反应被测参数与平均值的偏差程度,CU值越大,表明被测截面的压力分布均匀性越好。其表达式为

(4)
为表征燃烧室出口温度分布均匀性,现引入燃烧室出口温度分布系数(Outlet Temperature Distribution Factor,简称OTDF),其是衡量燃烧室出口温度分布好坏的重要标志。它定义为燃烧室出口界面内最高燃气总温与燃气平均总温之差与燃烧室温升的比值,定义式如式(5)所示,其中Tout_m为出口截面最高温度,Tin_ave和Tout_ave分别为燃烧室进、出口平均温度。

(5)
2.2 空气喷注总温
图5给出了燃烧室出口处总压的CU值、1-CV值随着空气喷注总温的变化趋势。由图5可知,出口总压的CU值、1-CV值均随空气喷注总温的提高而提高,两均匀性评价指标趋势一致,均指明随着空气喷注总温的提高,出口总压的均匀性也随之提高,CU值从0.363 2提高至0.477 8,提高了0.114 6,1-CV值从0.194 4提高至0.322 2,提高了0.127 8,提升数值接近。为探究空气喷注总温提高,出口压力均匀性提高的原因,给出了不同喷注总温下出口截面的总压分布,如图6所示。

图5 不同空气喷注总温下燃烧室出口截面总压CU值、1-CV值曲线

图6 不同空气喷注总温下燃烧室出口截面处总压分布曲线
由图6可知,随着空气喷注总温的提高,出口总压峰值变化不大,但总压上升至峰值的坡度却不断变缓,整体因此变得更加均匀。同时,单波模态下出口总压存在两个峰值,现给出了Case 1的总压云图,由图7(a)可知:出口总压的主峰值位于流场的滑移线附近,次峰值位于斜激波处。图7(b)给出了该时刻下的氧气组分分布,由图可知,滑移线附近是未参与爆震反应的空气的富集区,这是由于该工况为非均匀喷注,空气不能充分参与爆震反应,剩余的空气在斜激波的压缩作用下流入滑移线附件区域。该区域温度较低,而滑移线附近爆震产物流速是均匀变化的,因温度降低而导致该区域马赫数较高,如图7(c)所示,滑移线附近区域为燃料室内马赫数最高的区域,而高的马赫数使得该区域燃烧产物总压较大,即为出口总压的主峰值区域。斜激波处的出口总压较高是由于该处的反应产物受到了斜激波的压缩作用,使其出口总压增高。由图6可知:无论是出口总压的主峰值和次峰值,随空气喷注总温的提高均变化不大,影响出口总压均匀性的主要因素是主峰值之后,次峰值之前的燃烧产物出口总压的均匀性。随着空气喷注总温的提高,该部分燃烧产物出口总压均匀性变好的主要原因可能是随着空气喷注总温的提高,波前气态辛烷含量更高且反应混合物活性更高,致使爆震波强度更高,相同条件下爆震产物的出口总压更高,而出口总压的峰值随空气喷注总温的变化不大,因此出口总压分布更加均匀。
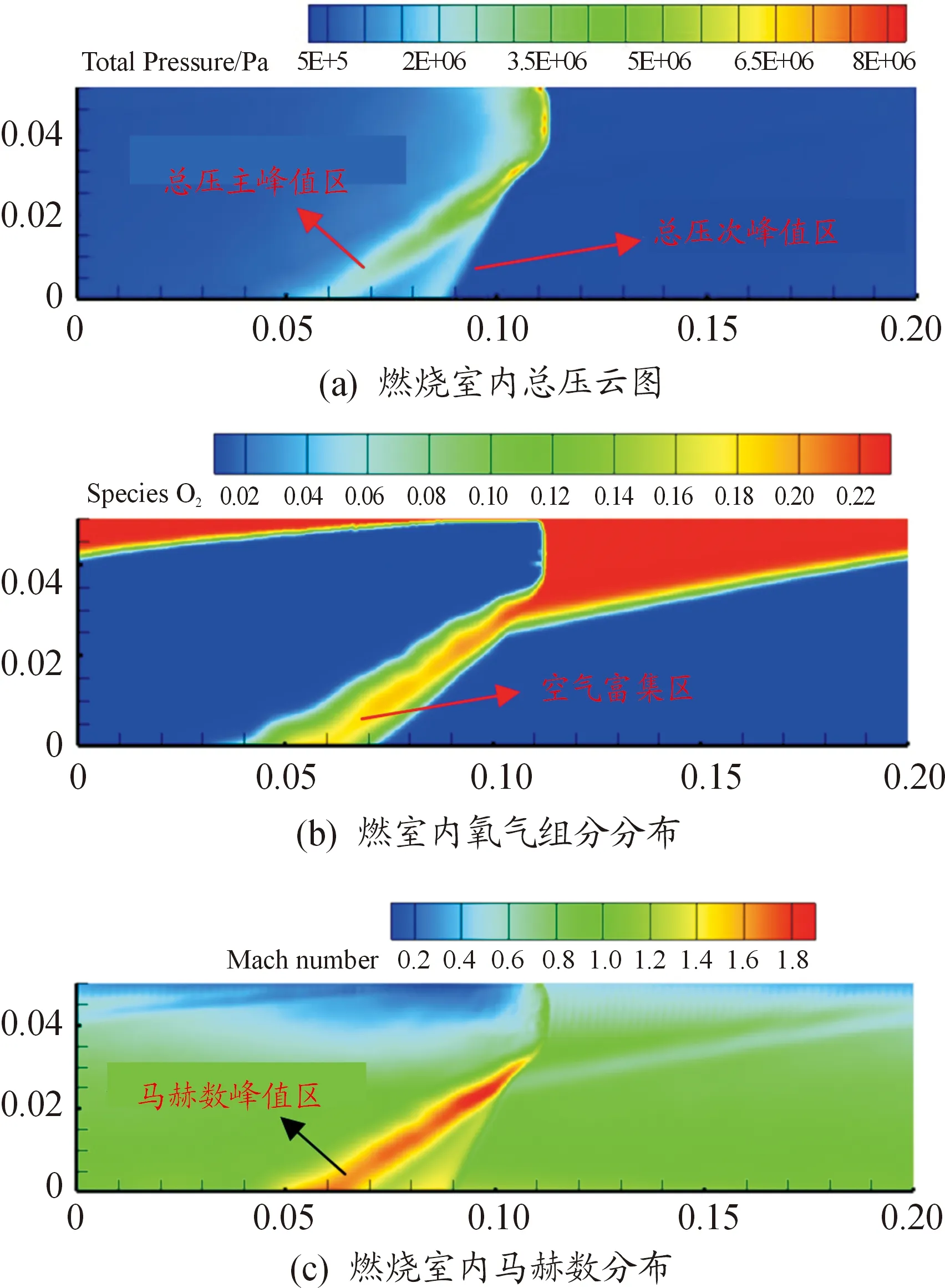
图 7 Case#1燃烧室内总压、氧气组分及马赫数分布云图
图8为OTDF值以及出口平均总温随空气喷注总温的变化趋势。由图可知,随着空气喷注总温从300 K提高至800 K,OTDF值从0.652 6降低至0.402 7,呈不断下降趋势,即燃烧室出口总温分布越来越均匀。为分析出口总温均匀性随空气喷注总温提高而变好的原因,给出了不同空气喷注总温下燃烧室出口总温分布,如图9所示。由图可知,不同空气喷注总温下的出口总温分布曲线均存在一个峰值平台及一个低洼,图10给出了空气喷注总温300 K下的总温云图,两图对照可知,出口总温分布曲线低洼处为滑移线附近区域,由图7(b)可知,未参与爆震燃烧的空气在斜激波的作用下在此区域汇集,导致该区域总温较低,导致出口总温分布曲线形成了一个低洼;出口总温分布曲线的峰值平台为斜激波与爆震燃烧产物相交的一块三角形区域,爆震燃烧产物受斜激波的绝热压缩作用总温迅速提高,致使出口总温分布曲线出现了一个峰值平台。图8给出了出口总温的平均值随空气喷注总温的变化趋势,可知随着空气喷注总温的增加,出口总温的平均值呈线性递增的趋势,由图9可知,随着空气喷注总温的提高,出口总温的整体值均不断提高,但出口总温极大值与极小值的差值却不断降低,空气喷注总温300 K时极值差为1 711 K,空气喷注总温800 K时极值差降为1 233 K;同时,主峰值与次峰值的差值也在不断降低,空气喷注总温为300 K、400 K、700 K、800 K下的出口总温主次峰值差依次为649 K、540 K、411 K、245 K,随着空气喷注总温的增加不断降低。燃烧室出口总温分布均匀性随空气喷注总温的增加而增加的原因应为: 斜激波处三角形区域的总温随空气喷注总温的增加而增加,但增加幅度远没有平均总温增加的幅度大;滑移线处低总温区随空气喷注总温的增加而增加,且增加幅度远超平均总温的增加幅度;斜激波处三角形区域的峰值总温与滑移线边缘处的次峰值总温之差随着空气喷注总温的提高而不断减小。这些原因共同导致了提高空气喷注总温能有效提高出口总温分布均匀性。

图8 OTDF值及出口平均总温随空气喷注总温变化曲线

图9 不同空气喷注总温下燃烧室出口总温分布曲线

图10 Case#1燃烧室内总温云图
2.3 辛烷射流间距
图11给出不同辛烷射流间距下的燃烧室出口截面总压CU值和1-CV值,由图可知,两均匀性评价指标趋势一致,随着辛烷射流间距增大,CU及1-CV均随之增大,随着辛烷射流间距从0 mm增加至8 mm,CU值从0.308 7增加至 0.446 7,增加了0.138,1-CV值从0.100 5增加至0.318 6,增加了0.218 1。两指标均表征随着辛烷射流间距增大,燃烧室出口总压均匀性变好。图12为不同辛烷射流间距下的燃烧室出口总压分布,由图可知,与上文分析类似,总压分布曲线存在两个峰值,分别对应着滑移线附近和斜激波附近的出口总压,随着辛烷射流间距的减小,总压主峰值越来越大,曲线越来越陡峭,而次峰值变化较小,因此改变辛烷射流间距主要是影响主峰值,即滑移线附近的出口总压而影响整个出口总压的稳定性的。图13给出了滑移线附近的马赫数和总压随辛烷射流间距的变化趋势,该区域的马赫数和总压也是整个出口截面的峰值马赫数和峰值总压,可以看到,峰值马赫数和峰值总压均随辛烷射流间距增大而减小,两者趋势一致,在其余条件基本不变的情况下,马赫数越高,总压越大。因此,增大辛烷间距能改善出口总压均匀性的原因应是:增大辛烷间距,滑移线附近马赫数减小,导致总压减小,而斜激波附近的总压变化较小,进而使得整个出口截面的总压均匀性增加。

图11 不同辛烷射流间距下的燃烧室出口截面总压CU值、1-CV值曲线

图12 不同辛烷射流间距下的燃烧室出口总压分布曲线

图13 出口峰值马赫数与峰值总压随辛烷射流间距变化曲线
图14为OTDF值随辛烷射流间距的变化趋势。由图可知,随着辛烷射流间距从0提高至8 mm,OTDF值从0.583 5降低至0.703 0,呈不断下降趋势,即燃烧室出口总温分布越来越均匀。由此可知,燃料喷注均匀性能影响燃烧室出口总温均匀性,燃料喷注均匀性越好,燃烧室出口总温均匀性越好。

图14 OTDF值随辛烷射流间距变化曲线
3 结论
采用均匀性评价指标CU,1-CV描述了空气喷注总温和辛烷射流间距对燃烧室出口总压均匀性的影响,空气喷注总温和辛烷射流间距越大,燃烧室出口总压均匀性越好。燃烧室出口截面总压分布曲线存在着两个峰值,分别对应着滑移线附近区域和斜激波附近区域。改变空气喷注总温,影响出口总压均匀性的主要因素是主峰值之后,次峰值之前的燃烧产物出口总压的均匀性;改变辛烷射流间距主要是影响主峰值,即滑移线附近的出口总压进而影响整个出口总压的稳定性。采用燃烧室出口温度分布系数OTDF描述了空气喷注总温和射流间距对燃烧室出口总温均匀性的影响,空气喷注总温越高,射流间距越小,燃烧室出口总温均匀性越好,并得出了增大辛烷间距能改善出口总温均匀性的原因应是:增大辛烷间距,滑移线附近马赫数减小,导致总温减小,而斜激波附近的总温变化较小,进而使得整个出口截面的总温均匀性增加。
