圆形降落伞下降轨迹控制研究
2021-02-23周文雅马瑞鑫胡欣涵王冠珺
周文雅,马瑞鑫,胡欣涵,王冠珺
(1.大连理工大学 航空航天学院,辽宁 大连 116024;2.辽宁省空天飞行器前沿技术重点实验室,辽宁 大连 116024)
降落伞是利用空气阻力实现气动减速的装置,由于其具有质量轻、减速效果好的优点,目前已被广泛用于航空航天领域[1-2],如返回舱回收、火星登陆、物资空投等。尽管降落伞在上述任务中已经发挥了其应有的气动减速作用,但由于没有主动控制系统,仍无法实现更为精确的投放任务。降落伞在下降过程中如果具备一定程度的控制能力,将具有更广阔的应用前景。以上述投放任务为例,在有控降落伞作用下,航天器能够更加精确地落入预定区域,缩小地面搜寻范围;在火星登陆过程中,能够使火星车落至更为平坦的安全区域;对于物资空投,更有利于物资落到指定区域。
国内针对主动控制降落伞的研究主要集中在翼型伞上。因为翼伞拥有高升阻比的气动性能、优良的滑翔能力以及良好的操作性[3]。但国外相关研究表明,翼伞存在每磅有效载荷成本过高的缺点[4]。为了降低成本,美国研发了低成本制导空投系统(AGAS),它基于现有的降落伞(C-9,G-12),通过4个气动肌肉(PMA)实现控制。这种方法虽然有不错的精度,但PMA的使用需要大量压缩氮气,导致系统质量较大,而氮气消耗也会使控制次数受到限制。Fields等[5]采用了一种更为简单的控制方法,该方法将风作为提供水平位移的唯一动力,并通过调整气动阻力来影响下降过程中的顺风漂移程度,能够一定程度提高降落伞的落点精度,但该方法无法实现特定点的降落,控制效果由风况决定。
本研究设计了一种更为简易可行的控制系统,即将所有伞绳分成四组,四组伞绳分别与控制箱内两组双轨绕线轮连接。绕线轮受步进电机控制,能够同时实现相对两组伞绳的收拉或释放。通过上述执行机构设计,能够实现伞衣形状和降落伞姿态的改变,最终产生朝向收绳一侧的水平控制力。所提控制机构相比于PMA,具有成本低、可重复利用等明显优势。本文给出了考虑上述主动控制机构的降落伞三自由度运动学模型,并基于模型开展了带有控制作用的降落伞下降轨迹及落点分布的仿真研究。蒙特卡罗仿真结果表明引入主动控制能够使降落伞在一定程度上抵抗不确定因素影响,提高降落伞的落点精度。
1 可控降落伞系统介绍
1.1 可控降落伞系统构成
对于传统降落伞,试验人员在投放前通常会测量降落伞下降阶段的风况,并根据预定的着陆点信息绘制出降落伞的预测轨迹和计算投放点。如果风况估计准确,并且实际投放点与计算投放点无偏差,那么降落伞的实际下降轨迹将会沿着预测轨迹飞行。然而,风况是实时变化的,难以准确测量,投放点的偏差也难以避免。因此,在实际投放中,降落伞的着陆点经常偏离预定落点。
带有主动控制机构的降落伞能够在一定程度上克服投放过程中的不确定因素(包括风扰及投放点误差等),使实际轨迹向预测轨迹靠拢,最终将负载投放至目标区域。可控降落伞实现轨迹调整的原理如图1所示。
可控降落伞系统主要包括:伞衣、伞绳、控制箱和负载。其中,控制箱主要包含:以STM32为CPU的控制板卡、电机及驱动系统、GPS导航模块。控制系统工作原理如图2所示。
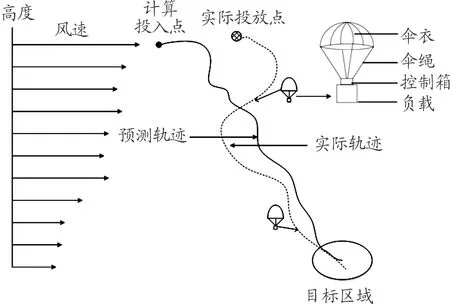
图1 可控降落伞轨迹调整原理示意图

图2 降落伞控制系统原理框图
1.2 收绳长度调整后的受力分析
根据前文介绍的伞绳收放控制原理,当降落伞一侧伞绳通过控制箱收拉后,对侧伞绳以相同长度释放。伞绳收放后的降落伞姿态及伞绳长度变化如图3所示。建立降落伞体固连坐标系O-XbYbZb和地面参考坐标系O-XYZ,考虑到降落伞的对称性,在纵平面O-XbZb内对系统进行受力分析。

图3 可控降落伞系统受力分析
图3中,P为伞衣压心,T和N为收放伞绳后降落伞所受的轴向力和侧向力。显然,当降落伞姿态发生改变后,伞衣内高压气体会因为收绳侧伞衣的下倾及放绳侧伞衣的上翘而产生一个指向伞绳收拉方向的水平气动力F。该气动力大小可通过对降落伞伞衣进行CFD模拟获得,本文不再赘述。研究中只对该力引起的轨迹改变能力进行仿真,而忽略伞绳长度改变量与气动力变化之间的复杂建模过程。
2 可控降落伞动力学模型
传统圆形伞的多自由度模型已经广泛存在[6-8]。通过对收放伞绳过程进行受力分析,文中给出引入等效控制量的圆形伞三自由度模型。此外,降落伞在下降过程中,需要考虑附加质量带来的影响[9-10]。对于三自由度运动模型,附加质量表达式为:
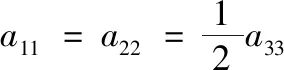
(1)
(2)
其中:a11、a22、a33为降落伞在体固连坐标轴O-XbYbZb上的附加质量;rp为降落伞投影半径。
降落伞压心处相对空气运动速度为Va;u、v、w为其在体固连坐标轴O-XbYbZb上的空速分量;ρ为大气密度;降落伞的阻力面积为SD,阻力系数为CD。则降落伞在不考虑风时受到的气动力为:

(3)
气动力在体固连坐标轴O-XbYbZb的分力为:
Xaero=-Faerocosθcosγ
(4)
Yaero=-Faerocosθsinγ
(5)
Zaero=-Faerosinθ
(6)
式中,θ和γ代表速度之间夹角,其表达式为:
sinθ=w/Va
(7)
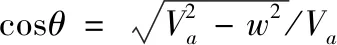
(8)
(9)
(10)
考虑到降落伞下降过程中风的影响,系统相对地面速度V可以表示为:
V=Va+Vw
(11)
式中,Vw为水平风速。
根据上文,收放伞绳后产生的水平控制力F,其在体固连坐标系Xb,Yb上分量为Fcx,Fcy。则系统动力学方程为:

(12)
式中,m为降落伞系统质量。
3 可控降落伞的制导控制
降落伞是依靠气动阻力进行减速运动的,其下降轨迹对风极为敏感,因而实际运动中很难实现精确快速制导。尽管本文中提出了可以利用伞绳收放的方式改变降落伞下降轨迹,但由于其控制能力有限,会导致轨迹的改变有一定滞后性。图1中给出了降落伞制导的基本思路,即让降落伞实际飞行轨迹尽量沿着预测轨迹,从而保证落点满足要求。但受降落伞控制能力限制以及下降过程中的不确定因素影响,实际下降轨迹不可能与预测轨迹完全重合。
为实现降落伞制导,可以以预测轨迹为中心,设定一个较大的包络半径router,router随高度的降低逐渐减小。这样就形成了一个向预测轨迹逐渐靠拢的外包络面。可以利用这个外包络面作为对降落伞实施控制的临界面,从而限制降落伞的飞行范围。同样,再引入一个内包络面,其半径rinner取固定值,其大小应依据降落伞气动特性及地面上落点精度要求确定。当降落伞进入内包络时,即视为完成控制。
当降落伞实际投放点偏离预定投放点距离大于rinner时,控制箱通过收放伞绳产生控制力,使降落伞返回到内包络以内。降落伞进入内包络面以后,控制箱恢复绳长,使降落伞进入正常状态。如果降落伞因为风力等作用由内包络面飘至外包络面时,再次实施控制,使降落伞返回到内包络面以内,以此反复,直至着陆,如图4所示。

图4 通过包络实施降落伞制导原理框图
降落伞控制系统利用预测轨迹与GPS测得实际轨迹信息的偏差信号形成控制指令。控制律采用PD控制,即:
Fcx=kpΔX+kdΔu
(13)

(14)
式中,Fcy与Fcx的比值等于预测轨迹与GPS测量位置在Y方向和X方向上的距离偏差之比,这样能够简便地实现两个通道的协同控制,使降落伞快速进入内包络面。
4 蒙特卡洛仿真
在利用降落伞实现定点投放的实际任务中,往往是根据预定落点和当地风速,对投放点进行估计或粗略计算。如果条件允许,也可以利用优化算法比较准确地反推出投放点位置和速度等信息。由于这部分内容与本文研究内容相关度不大,这里直接给出初始状态,并在考虑风的情况下计算得到预测轨迹。同时,以预测轨迹的落点作为预定落点。这里假定投放点状态(u0,v0,w0,X0,Y0,Z0)的具体数值为(-3,2,15,0,0,300),其中速度单位为m/s,距离单位为m。需要指出的是,这里所述的投放点是指降落伞展开后运动的起始点。如果考虑展开过程,即在此基础上修正投放点状态即可。通过对方程(12)进行积分,可以得到降落伞的预测轨迹,如图5所示。在此基础上,利用router和rinner给出内、外包络面。仿真得到的预测落点P0在O-XYZ空间坐标为 (211.50,-154.71,0)。
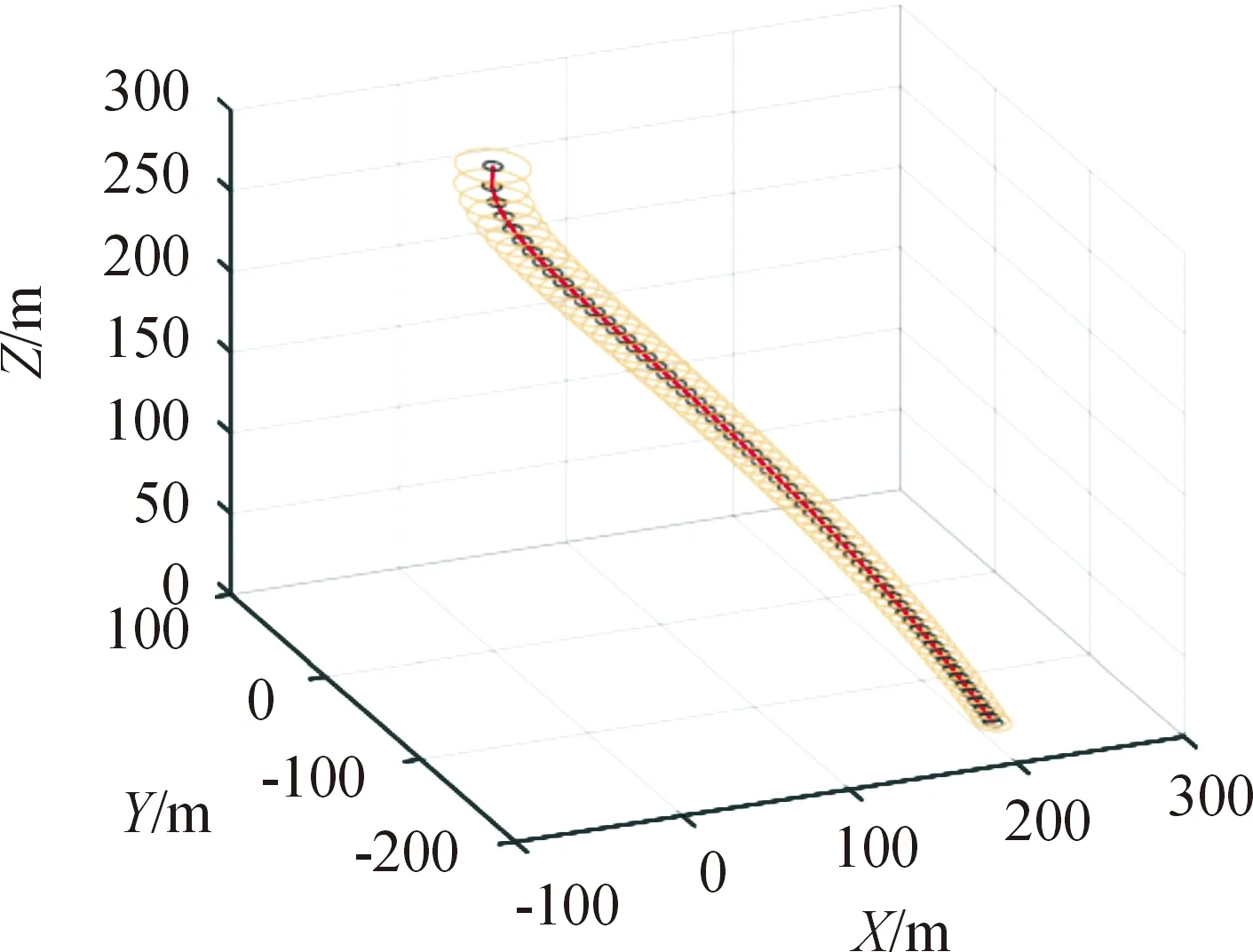
图5 理想状态下的降落伞预测轨迹
考虑到实际投放任务中不可避免地会受到多种干扰的影响。仿真中考虑的主要干扰因素有:降落伞投放速度偏差、高度偏差、气动参数偏差和风场测量偏差。取上述偏差量均为原值10%以内的随机数。
按上述仿真条件,给出1 000次样本点的无控降落伞下降轨迹蒙特卡罗仿真,结果如图6和图7所示。

图6 存在干扰情况下无控降落伞下降仿真轨迹

图7 存在干扰情况下无控降落伞落点分布仿真
由图6和图7可知,当降落伞不受控时,初始状态误差及外界扰动对其下降轨迹影响显著,落点分布广泛,近似呈正态分布规律,这与实际飞行试验结果相符。对图7数据进行统计,X方向上相对于预测落点的平均绝对偏差为32.43 m,最大绝对偏差可达到133.03 m;Y方向上的平均绝对偏差25.90 m,最大绝对偏差114.00 m;落点距离预测落点平均距离46.03 m,最远距离144.49 m。
在相同仿真条件下,对可控伞同样进行1 000次蒙特卡罗仿真,结果如图8和图9所示。

图8 存在干扰情况下可控降落伞下降仿真轨迹

图9 存在干扰情况下可控降落伞落点分布仿真
从图8可以看出,采用伞绳收放控制后,1 000次的降落伞下降轨迹呈现收敛状态,换言之,降落伞下降轨迹向预测轨迹靠拢。对图9数据进行统计,落点在X方向上平均绝对偏差3.94 m,最大绝对偏差19.55 m;Y方向上的平均绝对偏差3.54 m,最大绝对偏差12.56 m;施加控制后的落点距预测落点平均距离6.16 m,最远19.59 m。
对于近似满足正态分布的落点,可以通过圆概率误差(CEP)来描述降落伞的落点精度[11]。

(15)

(16)

(17)

(18)


(19)
计算可得,无控降落伞的CEP=42.84 m,而可控降落伞的CEP=5.61 m。由此可见,当降落伞具备控制能力后,其落点精度显著提升。
5 结论
本文提出了一种通过控制局部伞绳收放来改变圆形降落伞下降轨迹的方法。研究发现,降落伞将朝伞绳缩短的方向运动。依据上述特点,利用PD控制实现了基于轨迹内外包络面的闭环制导。在此基础上,分别开展了无控伞和可控伞的下降轨迹及落点的蒙特卡洛仿真并进行了对比分析。结果表明:有控降落伞下降轨迹能够呈现出收敛特性,说明下降轨迹对预测轨迹的跟踪效果良好;同时,落点精度也有显著提升。
后续研究中,将针对更为复杂、更多自由度的动力学模型进行控制系统设计,探讨伞绳收放对系统稳定性的影响,同时开展数值模拟与投放试验的验证工作。
