牙膏销售量问题的微分方程模型

王智峰 陈传军 孙丰云

【摘要】针对牙膏销售量问题，本文改进了回归分析模型，建立了微分方程模型进行销售量的预测，最后给出了灵敏度分析和稳定性分析.

【关键词】牙膏销售量;微分方程模型;回归分析模型

【基金项目】高等学校大学数学教学研究与发展中心资助（No.CMC20190408），烟台大学教学改革研究项目资助（No.jyxm2019041），山东省高等教育本科教改项目（No.Z2018S049）

一、引 言

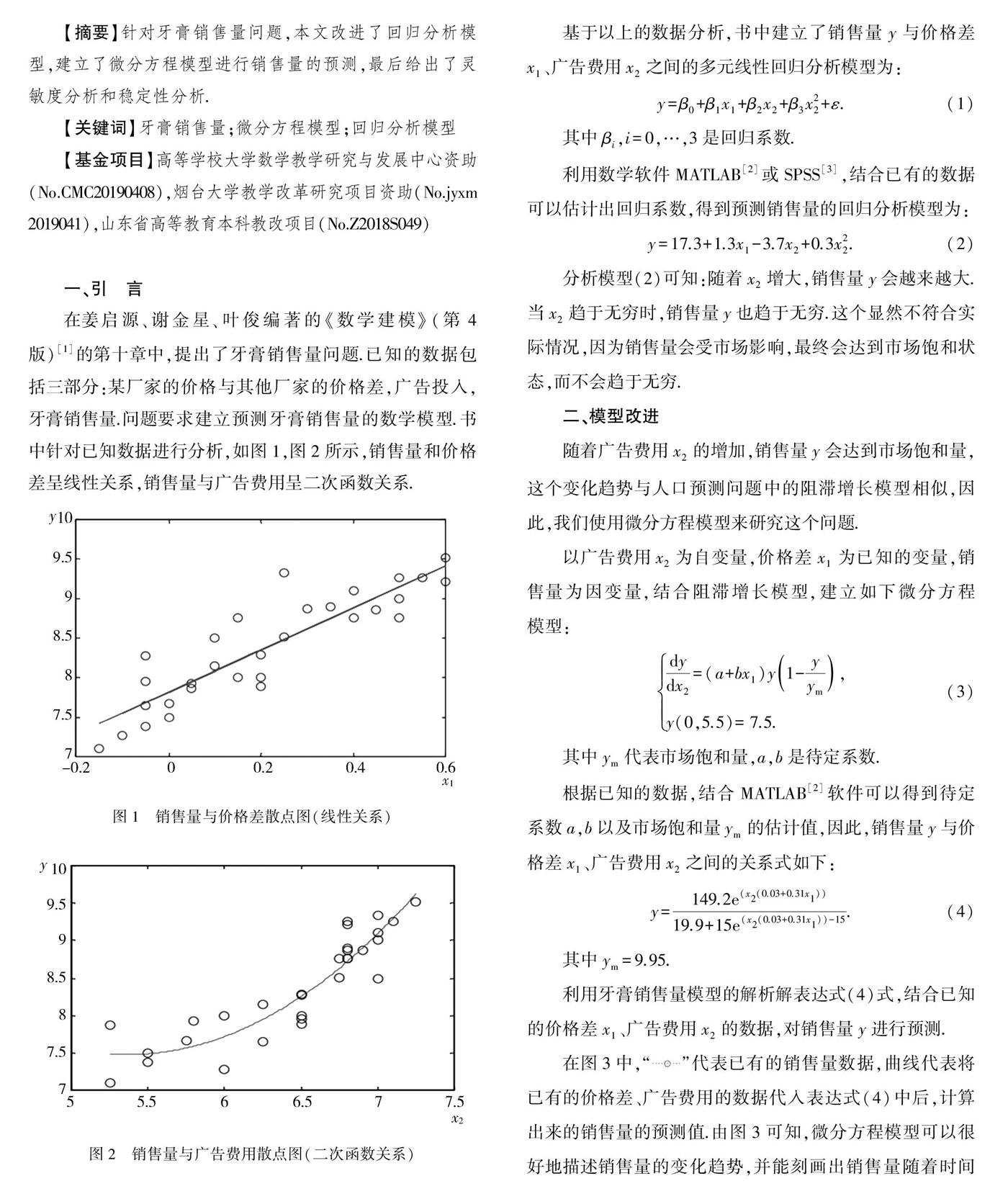
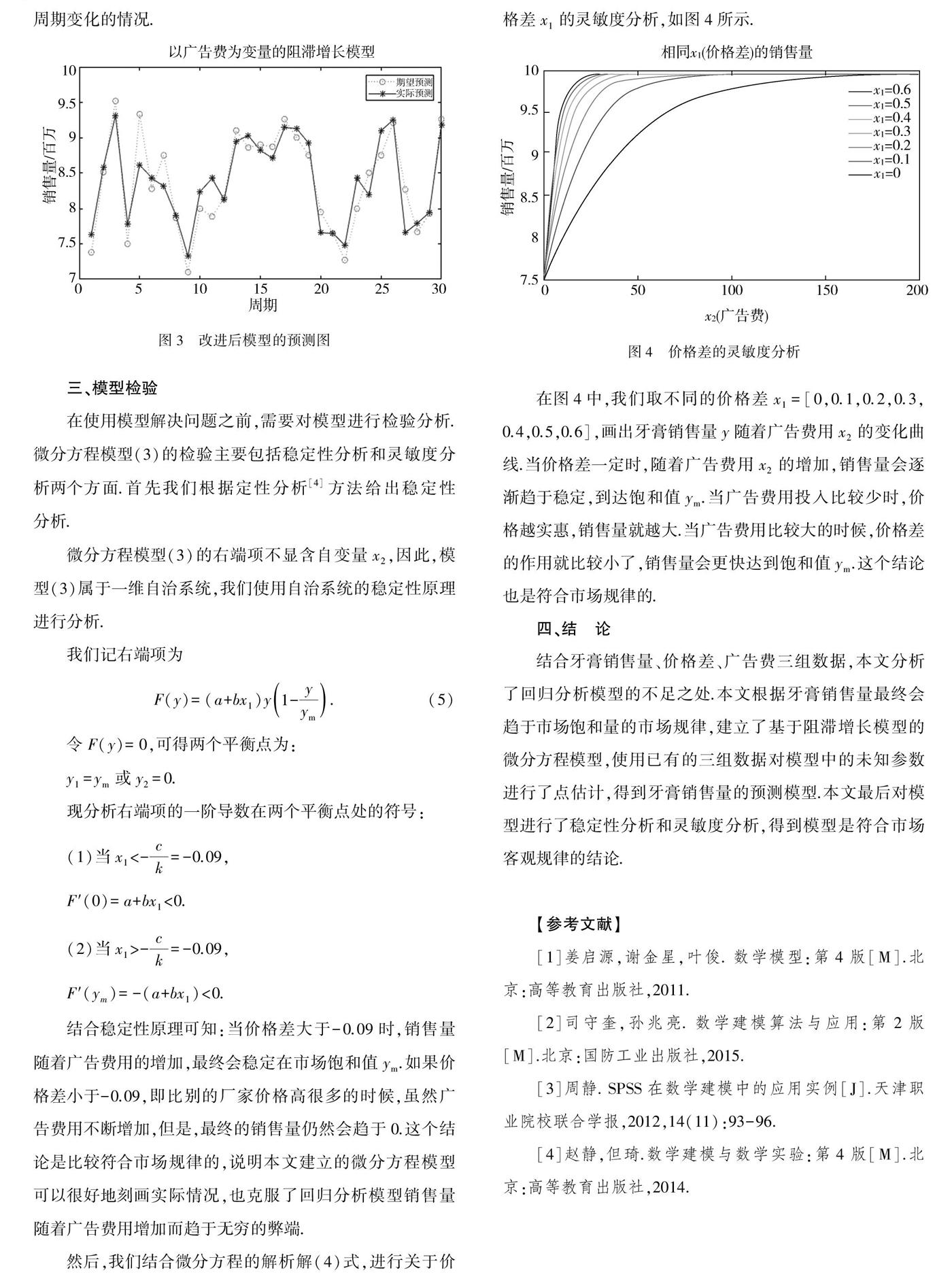
在姜启源、谢金星、叶俊编著的《数学建模》（第4版）[1]的第十章中，提出了牙膏销售量问题.已知的数据包括三部分：某厂家的价格与其他厂家的价格差，广告投入，牙膏销售量.问题要求建立预测牙膏销售量的数学模型.书中针对已知数据进行分析，如图1，图2所示，销售量和价格差呈线性关系，销售量与广告费用呈二次函数关系.

基于以上的数据分析，书中建立了销售量y与价格差x1、广告费用x2之间的多元线性回归分析模型为：

y=β0+β1x1+β2x2+β3x22+ε.（1）

其中βi，i=0，…，3是回归系数.

利用数学软件MATLAB[2]或SPSS[3]，结合已有的数据可以估计出回归系数，得到预测销售量的回归分析模型为：

y=17.3+1.3x1-3.7x2+0.3x22.（2）

分析模型（2）可知：随着x2增大，销售量y会越来越大.当x2趋于无穷时，销售量y也趋于无穷.这个显然不符合实际情况，因为销售量会受市场影响，最终会达到市场饱和状态，而不会趋于无穷.

二、模型改进

随着广告费用x2的增加，销售量y会达到市场饱和量，这个变化趋势与人口预测问题中的阻滞增长模型相似，因此，我们使用微分方程模型来研究这个问题.

以广告费用x2为自变量，价格差x1为已知的变量，销售量为因变量，结合阻滞增长模型，建立如下微分方程模型：

dydx2=（a+bx1）y1-yym，y（0，5.5）=7.5.（3）

其中ym代表市场饱和量，a，b是待定系数.

根据已知的数据，结合MATLAB[2]软件可以得到待定系数a，b以及市场饱和量ym的估计值，因此，销售量y与价格差x1、广告费用x2之间的关系式如下：

y=149.2e（x2（0.03+0.31x1））19.9+15e（x2（0.03+0.31x1））-15.（4）

其中ym=9.95.

利用牙膏销售量模型的解析解表达式（4）式，结合已知的价格差x1、广告费用x2的数据，对销售量y进行预测.

在图3中，“”代表已有的销售量数据，曲线代表将已有的价格差、广告费用的数据代入表达式（4）中后，计算出来的销售量的预测值.由图3可知，微分方程模型可以很好地描述销售量的变化趋势，并能刻画出销售量随着时间周期变化的情况.

三、模型检验

在使用模型解决问题之前，需要对模型进行检验分析.微分方程模型（3）的检验主要包括稳定性分析和灵敏度分析两个方面.首先我们根据定性分析[4]方法给出稳定性分析.

微分方程模型（3）的右端项不显含自变量x2，因此，模型（3）属于一维自治系统，我们使用自治系统的稳定性原理进行分析.

我们记右端项为

F（y）=（a+bx1）y1-yym.（5）

令F（y）=0，可得两个平衡点为：

y1=ym或y2=0.

现分析右端项的一阶导数在两个平衡点处的符号：

（1）当x1<-ck=-0.09，F′（0）=a+bx1<0.

（2）当x1>-ck=-0.09，F′（ym）=-（a+bx1）<0.

结合稳定性原理可知：当价格差大于-0.09时，销售量随着广告费用的增加，最终会稳定在市场饱和值ym.如果价格差小于-0.09，即比别的厂家价格高很多的时候，虽然广告费用不断增加，但是，最终的销售量仍然会趋于0.这个结论是比较符合市场规律的，说明本文建立的微分方程模型可以很好地刻画实际情况，也克服了回归分析模型销售量随着广告费用增加而趋于无穷的弊端.

然后，我们结合微分方程的解析解（4）式，进行关于价格差x1的灵敏度分析，如图4所示.

在图4中，我们取不同的价格差x1=[0，0.1，0.2，0.3，0.4，0.5，0.6]，画出牙膏销售量y随着广告费用x2的变化曲线.当价格差一定时，随着广告费用x2的增加，销售量会逐渐趋于稳定，到达饱和值ym.当广告费用投入比较少时，价格越实惠，销售量就越大.当广告费用比较大的时候，价格差的作用就比较小了，销售量会更快达到饱和值ym.这个结论也是符合市场规律的.

四、结 论

结合牙膏销售量、价格差、广告费三组数据，本文分析了回归分析模型的不足之处.本文根据牙膏销售量最终会趋于市场饱和量的市场规律，建立了基于阻滞增长模型的微分方程模型，使用已有的三组数据对模型中的未知参数進行了点估计，得到牙膏销售量的预测模型.本文最后对模型进行了稳定性分析和灵敏度分析，得到模型是符合市场客观规律的结论.

【参考文献】

[1]姜启源，谢金星，叶俊. 数学模型：第4版[M].北京：高等教育出版社，2011.

[2]司守奎，孙兆亮. 数学建模算法与应用：第2版[M].北京：国防工业出版社，2015.

[3]周静. SPSS在数学建模中的应用实例[J].天津职业院校联合学报，2012，14（11）：93-96.

[4]赵静，但琦.数学建模与数学实验：第4版[M].北京：高等教育出版社，2014.