基于最小距离求交的狭叶锦鸡儿叶片横切面宽度测量*

王海超，石鑫，杨建，程林，李宝兵，王春光

(1. 内蒙古农业大学能源与交通工程学院，呼和浩特市，010018； 2. 内蒙古农业大学机电工程学院，呼和浩特市，010018)

0 引言

叶片作为植物进行光合作用和蒸腾作用的主要器官，对环境变化最为敏感，叶片形态的变化是对环境因子变化的综合响应结果，叶片横断面宽度常作为衡量植物抗旱性的重要指标，是研究植被对胁迫因子响应机制的重要依据[1-5]。大量学者对植物叶片横切面宽度与抗旱性间相关性进行了研究,结果表明：随着干旱胁迫程度加剧，叶片横切面厚度增大，叶片解剖结构横断面为V型向内弯折，宽度减小，叶型逐渐向针状或刺状进化，以此提高贮水能力，降低水分蒸腾[6-10]。

传统叶片横切面宽度常采用显微镜交互进行测量，该方式不但效率低、劳动强度大，且常受人为主观因素影响，误差较大，重现性差。随着图像处理技术的发展，图像处理技术被广泛应用于叶片几何尺寸测量。杨红云等[11]提出了基于机器视觉的水稻叶片几何参数测量方法，实现了水稻叶片面积、长度、宽度、茎叶夹角测量，与手工测量比较，叶片面积计算误差、长度误差及茎叶夹角误差分别在5%、0.67%、2%以下。郭斯羽等[12]提出了一种基于图像长叶柄轴对称叶片中轴长度测量方法，该算法首先采用阈值分割提取叶片区域，然后利用骨架提取算法提取叶片区域骨架，最后对骨架进行拟合，确定叶片长度；崔世钢等[13]通过灰度化、几何校正、中值滤波去噪、阈值分割和轮廓提取等算法，实现了叶片面积和周长的提取，拟合优度为0.994 8～0.999 4；王健等[14]使用透视变换亚像素角点监测法对叶片图像进行校正，采用K-means聚类算法对图像进行分割，实现了叶面积测量，相对误差为0.01%～1.42%；Liu等[15]开发了一种基于Android手机平台的叶片几何参数测量系统，该系统可较准确实现叶片长度、宽度、周长和面积测量。虽然采用图像处理算法对叶片几何参数测量算法较多，但目前可见的叶片长度和宽度测量算法，大多都是计算目标区域最小外接矩形边长得到，与真实测量方式和数值间存在差异。

叶片横切面宽度的准确测量，对揭示胁迫因子对植物叶片形态结构的影响，研究植被适应性具有重要意义，由于叶片解剖结构图像具有纹理多、结构复杂、光照不均匀、形态不规则等特征，其制约了传统叶片横切面宽度识别算法应用。因此，本文以狭叶锦鸡儿叶片解剖图像为研究对象，首先将采用同态滤波对叶片横切面图像进行光照补偿；接着将灰度化后图像采用最大类间方差法(Otsu)将叶片整体从背景中分离，并使用形态学处理算法，消除初分割边缘毛刺，填充存在的孔洞；然后采用Sobel算子提取边缘，使用快速行进骨架提取算法提取目标骨架；最后采用本文提出的最小距离求交法确定宽度测量点，使用欧几里得算法计算两点间图上距离，将其除以对应比例关系，得到实际叶片横切面宽度。

1 材料与方法

1.1 图像获取

采用石蜡切片法对FAA液固定后的成熟狭叶锦鸡儿叶片进行切片，并成片，具体过程包括软化、脱水、透明等步骤，详见文献[16]。使用YYS-80E型光学生物显微镜和配套CM1400摄像机拍照、存储及测量，考虑到视野范围，选择×4目镜，图像分辨率为896像素×684像素，格式为jpg，图像颜色空间模型为RGB，除木质部为红色外，叶片目标区域整体为绿色。由于手工制片受温度、染液浓度、相机曝光增益比等因素干扰，图像存在光照和色差不均等现象，部分图像如图1所示。

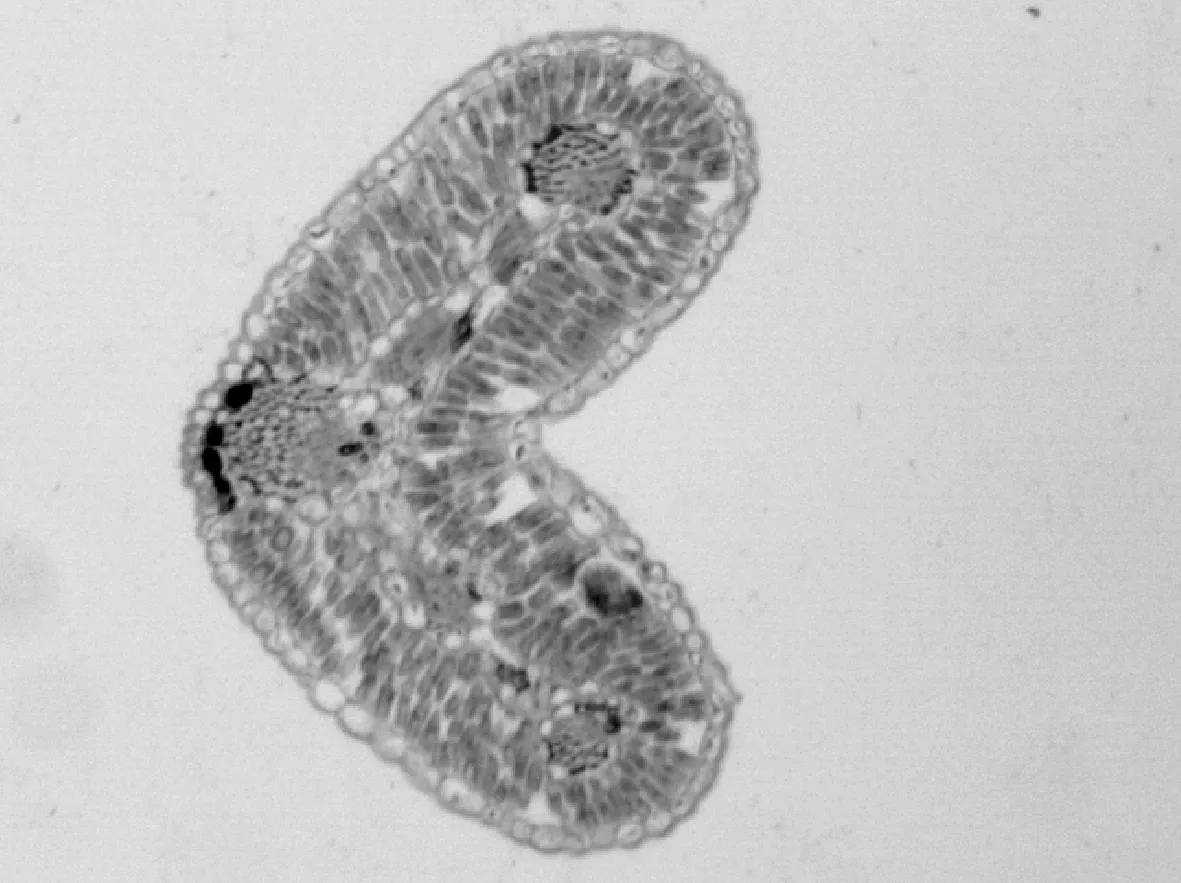
(a) 第一组

1.2 图像分割

1.2.1 光照补偿

针对显微图像存在光照不均和色差现象，可通过光照不均匀校正算法进行补偿，光照补偿后的图像不但能够改善视觉效果，而且可提高后续图像分割和指标提取精度，其是图像预处理过程中十分重要环节。本文采用动态巴特沃斯同态滤波算法，对HSV变换后的叶切片图像进行光照补偿，具体详见文献[17]。

1.2.2 图像分割

将光照不均和色差校正后叶切片图像从背景中准确分离是后续指标准确提取关键，最大类间方差法(Otsu)在图像分割领域应用十分广泛，其基本思想为通过最优阈值T，将图像f(x,y)中的L个灰度级，第Ni个像素分成目标区域C0和背景区域C1背景区域两类，当C0和C1间方差达到最大，类内方差最小时，目标区域和背景被完全分离。

1.2.3 形态学处理

形态学处理可改善结构元素形状，光滑图像边缘等。形态学重建的孔洞填算法可智能识别二值图像孔洞，并完成填充，实际应用十分广泛，其表达式

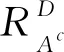
(1)

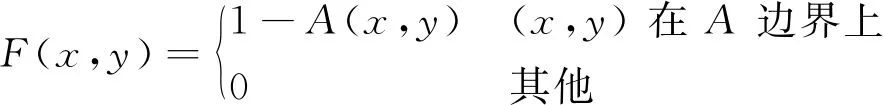
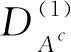
式中：F——除边界为1-A(x,y)，其余均为0；

A——二值图像；

B——结构元；

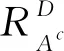
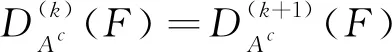
1.2.4 分割质量评价

本文对分割质量进行定量评价，评价指标分别为分割误差R、过分割误差OR和欠分割误差UR，其值越小，图像分割质量越好，目标分割越精确，详见文献[17]。拟采用Photoshop手动分割擦拭出叶片横切面真实区域，将其作为上述3个指标的基准。

R=|A-A·|/A×100%

(2)

(3)

UR=|A-(A∩A·)|/A×100%

(4)

式中：A——真实面积；

A·——目标面积；

1.3 叶片横切面宽度测量

1.3.1 图像边缘及骨架提取

由叶片横切面图像结构特点可知，叶片整体部分分出后，实际叶片横切面宽度测量为横断面展度最远点。因此本文在充分分析图像特点基础上，首先采用Sobel算子提取叶片横断面边缘，然后采用快速行进骨架提取算法提取其骨架，其相较传统基于数学形态学和基于距离变换骨架提取算法，具有抗干扰能力强、精度高、连续性强等特点。基于快速行进骨架提取算法可实现亚像素级，详见文献[18]。

1.3.2 最小距离求交法

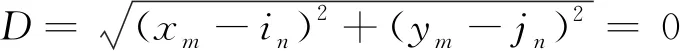
2 试验与结果分析

2.1 试验方法

1) 为验证光照补偿有效性，从已有图像中选取颜色不均的图像30幅，采用最大类间方差法(Otsu)对原始叶片图像初分割，然后采用半径为5的圆形结构元对图像进行闭开操作，接着用形态学重建法填充孔洞，最后采用8邻接标记图像连通分量，所标记面积最大联通分量即为叶片整体部分，从而实现叶切片整体部分提取。对采用动态巴特沃斯同态滤波算法处理过的30幅图像重复以上处理过程。分别比较同态滤波前后分割的误差。

2) 为验证骨架提取效果，分别采用基于数学形态学细化骨架提取算法，基于距离变换骨架提取算法，基于快速行进骨架提取算法提取叶切片骨架，并比较提取效果。

3) 为验证本文算法精度，需将骨架进行拓展，首先选择多项式拟合和高斯拟合算法对骨架点进行拟合，并比较拟合精度，然后采用本文提出的环形结构提取算法确定宽度测试点，使用欧几里得算法计算两点间图上距离，将其除以对应比例0.60 pi/μm，得到实际叶片横切面宽度。将对比测量结果，分析本文算法有效性。

2.2 结果与分析

1) 以图1(a)为例图，叶片整体部分分割效果示例如图2所示，分割精度如表1所示。就本例图而言，经光照补偿后的图像，Otsu算法最优阈值T为61，可分性度量η为0.892。由图2(a)可以看出，图像经同态滤波后，光照不均和色差得到明显改善，图像质量得到有效提升；由图2(b)知，图像未经光照补偿分割时，存在明显的过分割和漏分割现象，光照补偿后分割效果得到改善；由表1可知，光照补偿前，采用Otsu算法、形态学操作、孔洞填充、连通域标记等算法处理后，图像分割误差R均值约为15.84%，过分割误差OR均值约为10.86%，欠分割误差UR均值约为4.85%，经光照补偿后，图像分割误差R均值约为5.37%，过分割误差OR均值约为2.10%，欠分割误差UR均值约为3.31%，分别下降了10.47、8.76和1.54个百分点。由此可以发现，采用动态巴特沃斯同态滤波后图像质量和视觉效果得到改善，而且还提高了图像分割精度。

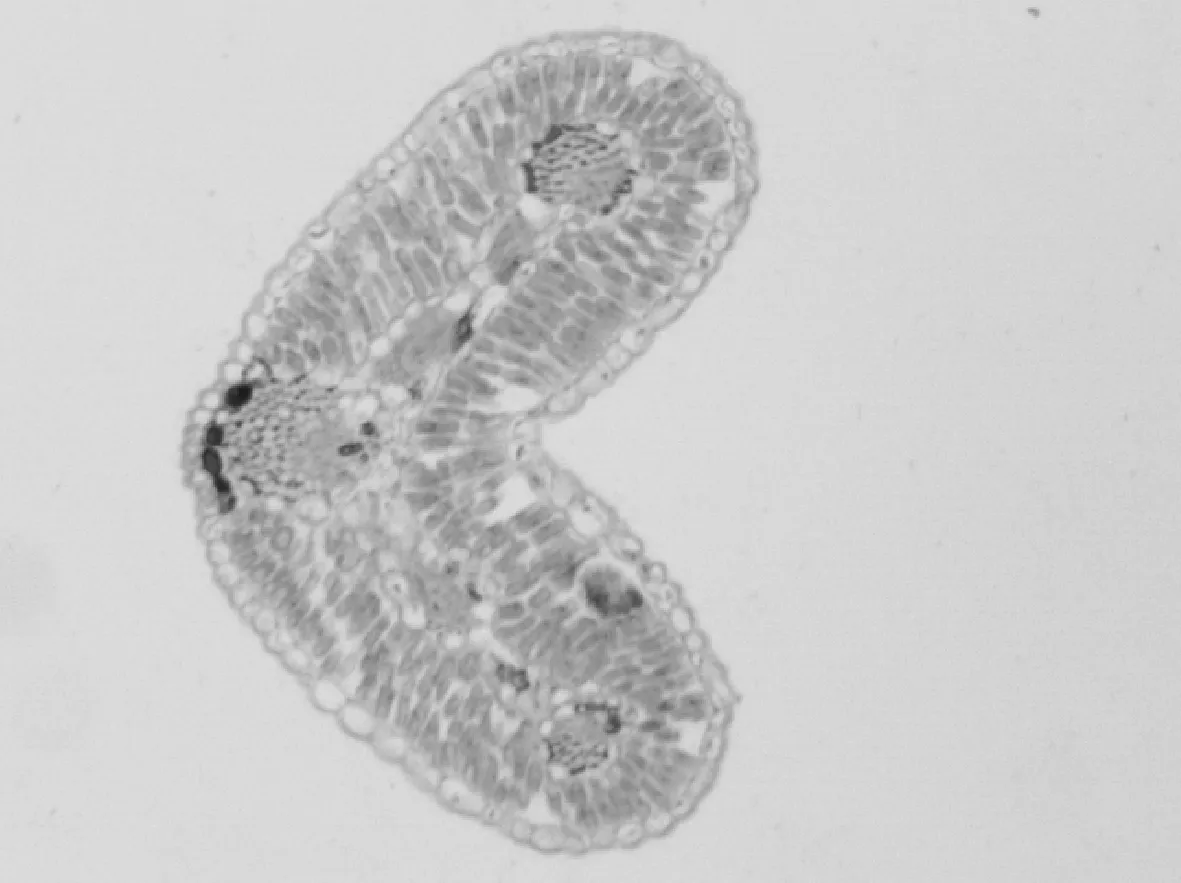
(a) 同态滤波后

表1 分割效果的客观评价

2) 基于数学形态学细化骨架提取算法、基于距离变换骨架提取算法和基于快速行进骨架提取算法分割结果如图3所示，为了便于观察，将骨架附于原图，并将选定区域放大10倍。由图3可知，基于数学形态学细化骨架提取算法提取的骨架连续，但重复点较多，虽经过细化处理，但宽度较大；基于距离变换骨架提取算法提取的骨架虽没有重复点，但出现了骨架不连续现象；相较以上两种算法，基于快速行进骨架提取算法效果较好，不但可有效消除毛刺、多像素宽等缺陷，且骨架连续性较好。

3) 采用多项式拟合和高斯拟合算法对骨架点拟合效果如图4所示，拟合精度如表2所示。由表2知，采用多项式曲线拟合算法拟合骨架，当幂级数n=8时，均方根误差RMSE约为1.416，而且出现了过拟合现象；采用高斯曲线拟合算法拟合骨架，当幂级数n=4时，均方根误差RMSE小于1，约为0.718，n值继续增大，均方根误差变化不大。

采用最小距离法求交效果图如图5所示，测量结果如表3所示。由图5可知，确定的A、B交点相对准确；由表3可知，采用ToupTek Toupview软件对30片供试叶切片宽度均值约为645.31 μm，本文算法测量均值约为646.31 μm，相对误差约为0.42%，均方根误差RMSE约为3.065，精度基本能够达到测量要求。

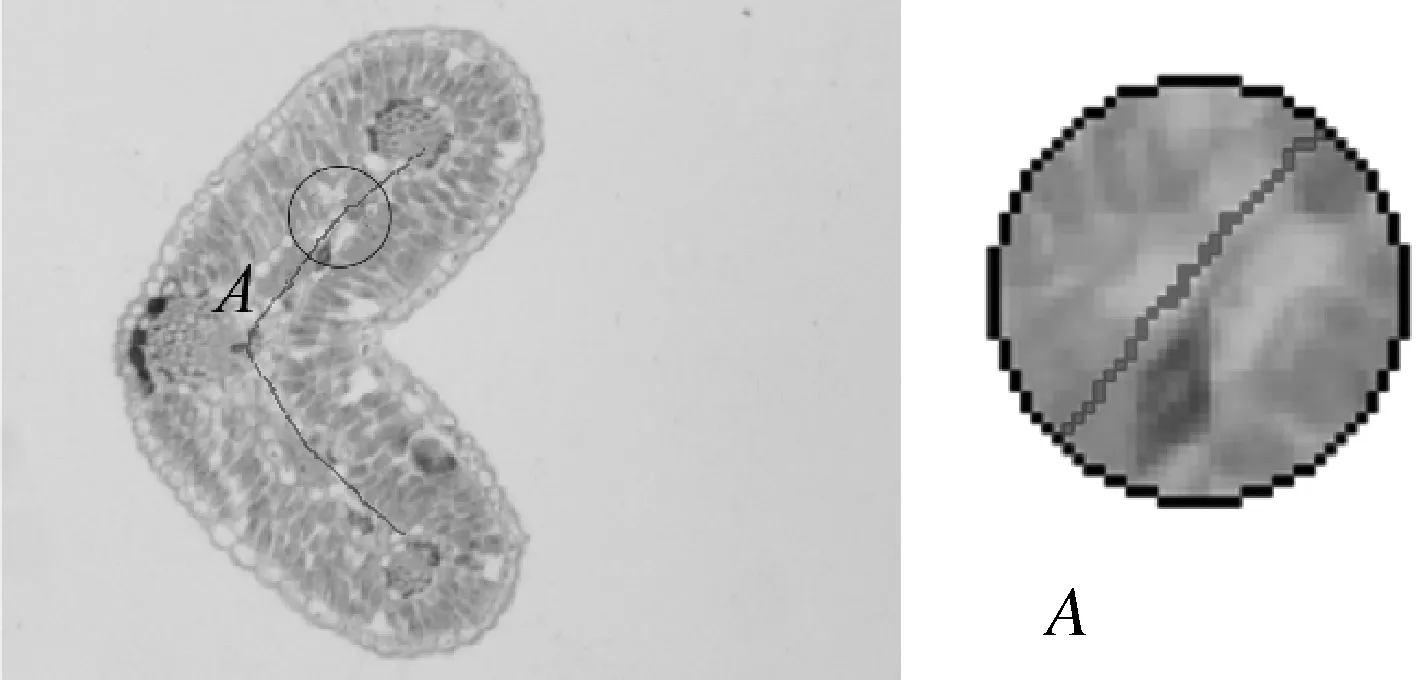
(a) 基于数学形态学细化骨架提取效果图

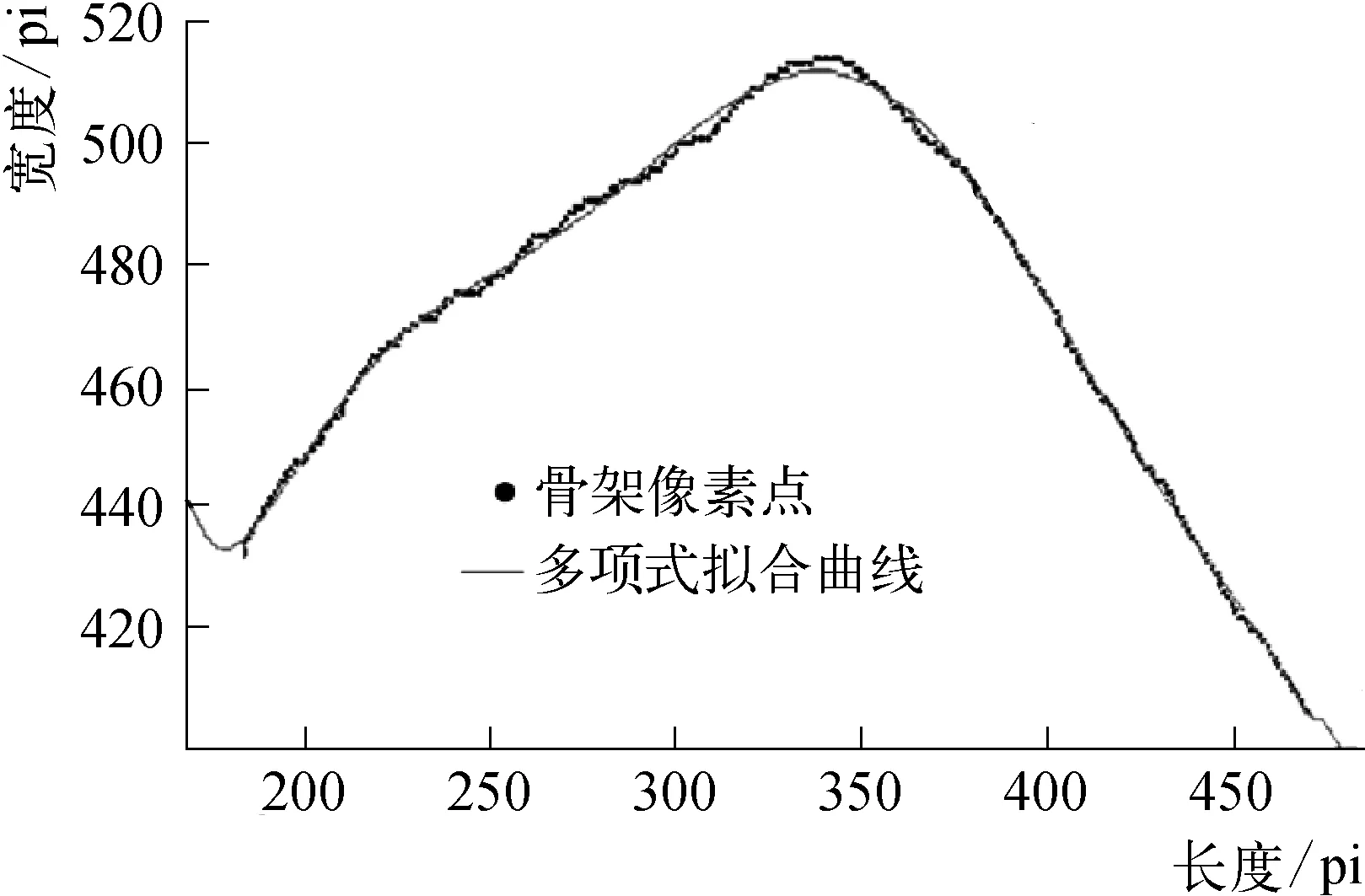
(a) 多项式拟合骨架效果图

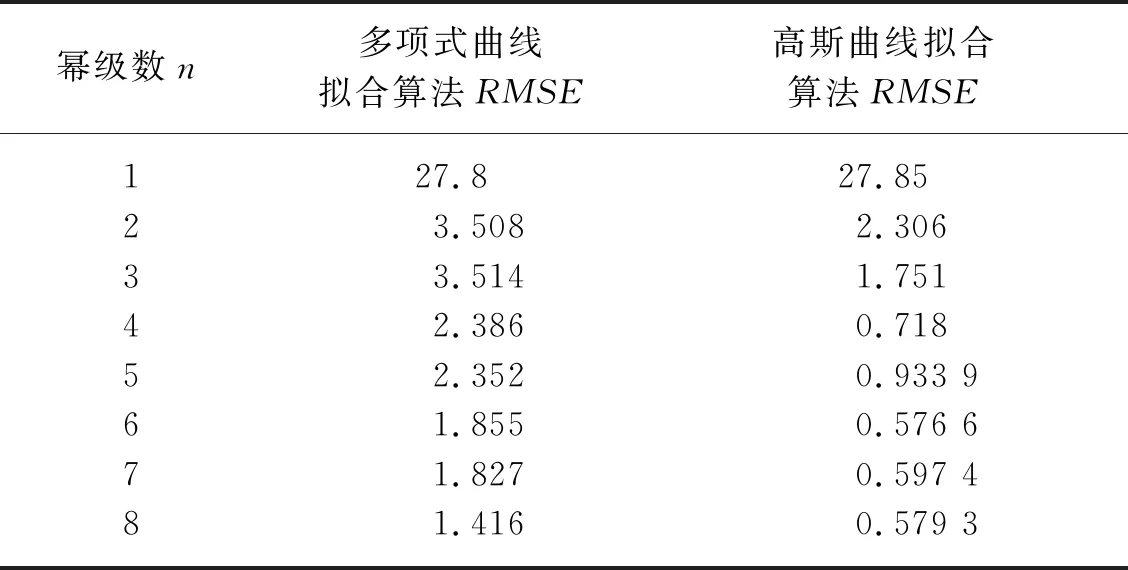
表2 拟合精度定量评价

表3 最小距离求交与交互测量值对比

图5 最小距离法求交结果示例

3 结论

本文以狭叶锦鸡儿叶切片为研究对象，针对叶片宽度测量问题，通过光照不均校正、最大类间方差(Otsu)分割、形态学处理、骨架提取、拟合拓展和最小距离求交法，实现了叶片横切面宽度K测量，通过实验得出以下结论。

1) 采用最大类间方差法(Otsu)将同态滤波后的叶片整体从背景中分离，并使用形态学开操作法，消除其边缘毛刺和细小连接等，使用形态学重建算法，进一步填充分割后孔洞，通过连通域标记提取后，分割误差R均值约为5.37%，过分割误差OR均值约为2.10%，欠分割误差UR均值约为3.31%，分割效果优于为进行光照补偿。

2) 采用高斯曲线拟合算法对叶片整体部分骨架进行拓展，均方根误差RMSE约为0.796，优于多项式拟合算法结果；本文提出的最小距离求交点法，交点确定较准确，对供试叶片宽度测量均值约为646.31 μm，均方根误差RMSE约为3.065，相较ToupTek Toupview软件交互测量，相对误差约为0.42%，满足实际测量需求。当叶切片完整度较高时，本文算法测量结果精确，但叶切片质量不高时，本文算法测量误差较大，在今后进一步研究中，将加强提高算法鲁棒性研究，改善本文算法存在不足。