面向嵌入式的卷积神经网络硬件加速器设计

唐 蕊，焦继业，徐华昊

西安邮电大学 计算机学院，西安 710121

近年来，随着人工智能应用需求的快速增长，神经网络在学术研究和人工智能相关应用中蓬勃发展，并被应用于各种新兴的智能领域，如语音识别、图像分类等[1-4]。与此同时，加速卷积运算的硬件设计随之产生，针对神经网络推理的加速芯片已成为该领域重要的发展方向。

目前针对嵌入式端的神经网络加速优化，可以从模型压缩和优化加速运算两方面出发。从模型压缩角度讲，主要通过一定的优化方式来减小网络模型所占的存储空间，其中包括模型剪枝和模型参数低精度量化，参数的低精度量化对卷积网络中所有的运算加速都有效。从优化加速运算来讲，主要针对神经网络中的结构及权重参数的共享性进行相关硬件单元的设计，可用来加快神经网络的执行速度，优化设计的整体性能[5-7]。文献[1]采用了数据量化的方式，分析参数的取值范围，先确定量化的大致精度，然后选出最优量化精度，将原有参数从64 位浮点数量化为16 位定点数来表示，显著提升了运行速度，并提出相应的计算和存储设计，结果证明对卷积网络的性能有明显提升。文献[2]采用动态可配置定点数据来表示网络的权重和激活函数，在推断的过程中也可保持较高的准确率。结果表明，低精度量化后，在尽可能保持准确性的前提下，对内存容量和带宽的需求减小了50%。文献[3]在进行数据量化时，采用的是非线性量化，分析每一层参数的范围，确定数据量化的系数，对参数进行量化。谷歌TPU、NVIDIA Tesla V100、寒武纪DianNao[8-9]等是具有代表性的人工智能加速芯片，均采用了数据低精度量化的思想。在卷积神经网络中，网络各层参数范围各有差异，不同网络层权重的概率分布也有一定的差异。

一般来说，神经网络中的参数主要为32 位和64 位浮点数。然而，随着卷积神经网络模型的层数越来越多，其中权重参数数量也在增长。因此网络中包含的运算量愈加复杂，在一些场景上限制了相应网络模型的部署，需要借助模型压缩、优化加速运算等方法突破瓶颈[10-11]。通常情况下，嵌入式设备上计算资源是非常有限的，并且对功耗有着比较严格的要求，使得嵌入式设备的计算能力与存储访问能力受到了极大的限制。卷积神经网络中较为复杂的运算及存储访问需求使其在嵌入端的部署成为难点[12]，其中最为复杂的便是卷积运算。针对以上情况，神经网络模型在嵌入式设备上进行实现，需在保持准确性的前提下，解决其运算量大、存储需求大的问题[13]。

为了解决该问题，本文主要采用了将模型参数量化与硬件设计加速运算的方式结合起来的方法，更大程度优化网络模型。首先，提出并设计了针对嵌入式平台的低精度定点量化单元，研究了神经网络中经过训练后的数据分布范围及数据量化原理，根据最小误差量化算法设计了动态低精度量化单元，对数据进行低精度定点量化。在保持精度的同时减小了数据的位宽，进而减小了对内存及带宽的需求。其次，设计了可循环调用的矩阵卷积运算的结构，使量化后的数据可并行执行卷积运算，进而缩短了运算的执行时间，提升整体性能。本设计在减小网络中数据位宽，实现神经网络轻量化的同时，又保证了数据精度，可用在对实时性要求高的嵌入式设备中。

1 低精度动态量化研究

1.1 动态量化原理

在神经网络中，对其中的FP32 类型的参数进行INT16 量化，使其模型更小，推断更快。对参数量化精简的方式之所以有效，广义来说，是由于经过训练后的神经网络对噪声和较小的扰动具有鲁棒性，意味着在将数据量化并做相关舍入处理后，卷积网络的推断过程依旧可以得到一个相当准确的结果[14-15]。因此参数量化在几乎不牺牲精度的情况下，可使执行速度加快，进而有效提升对数据的处理能力。低精度量化从某个角度来说，是一种数据在不同范围空间的映射[16]。经过大量研究，针对神经网络中的低精度量化，总结得出下面结论：

（1）相比于FP32模型，低精度量化后卷积速度得到大幅提升。

（2）量化后的网络模型权重所占空间降低60%～70%，有效提升对数据的处理能力。

（3）INT16 量化可以在提升运行速度的同时，可最大程度保持准确性。

对于INT8量化来说，在追求运行速度的同时，准确性也有更大程度的损失，本设计旨在实现高性能的同时，也尽可能保持数据最好精度，因此将输入的FP32数据量化为INT16定点数据，然后进行卷积运算。整体设计的原理如图1，首先需要分析神经网络中参数的数值分布范围，如第一层神经元的输入、权重等，然后进行数据的低精度量化，并将量化后的数据放入存储。在执行卷积运算时将数据从存储中取出，下一时钟周期送入并行卷积运算单元进行卷积计算，实现了取数据和运算的流水结构。卷积运算后将结果依次送至下一个存储。重复调用卷积运算单元进行卷积运算。

然而，针对神经网络来说，从浮点数据量化而来的每个定点数据，以及每个中间参数的精度都是不确定的，固定精度量化会产生一些不必要的误差。经过大量研究，结果表明，在对不同精度的数据进行低精度量化时，若采用固定精度定点量化，则量化后的数据精度越高，数据准确性也越高。然而对于同等位宽数据进行量化时，采用动态多精度量化的情况下，数据准确性更高。当采用16 bit 的数据动态低精度量化时，引入的误差很小[17]，并且对内存容量和对带宽的需求减小了50%。相比于固定精度定点量化，动态多精度定点量化更适合神经网络中的卷积运算，进而最小化卷积网络中数据量化过程产生的误差。

因此针对该问题，在本设计中使用动态多精度定点量化方法对浮点数据进行量化。

浮点与定点之间的量化关系如下所示：

图1 量化卷积运算原理示意图

其中，x表示浮点数，q表示这个浮点数对应的Qn型定点数。

在量化单元的设计过程中，采用了最小误差量化算法的思想，如式（3）：

其中，Dfloat为输入的原浮点型参数，Dfixed(L,Q)为量化后的定点数据。由于网络中的所有参数的精度不完全一致，根据输入数据的数值范围，选择合适的数据量化比例并使用Q 格式表示，通过动态设置数据的Q 值，即可调整量化后的定点数据精度，进而最小化定点量化所带来的误差。

1.2 数据类型对比

计算机中常用的数据类型有两种，包括定点数和浮点数。一般来说，定点格式允许表示的数值范围有限，但要求的处理硬件单元比较简单。浮点格式则相对复杂，浮点运算广泛应用于通用处理器，如图形处理器[18]。

定点数的小数点位置是固定的。定点运算相比于浮点运算有着更低的硬件成本，被广泛应用于神经网络加速器中，定点数可以在存储数据时节省更多的内存容量和带宽资源。

1.3 定点数的表示格式——Q表示法

一个定点数据的最大数值范围取决于所给定的字长。数值中定义整数最低位和小数最高位之间的方式被称为定标，即指示了小数点的位置。定标有两种方法，包括Q 表示法和S 表示法，本设计中的量化部分借助Q表示法完成。

16 位定点数的部分Q 值以及每个Q 值的表示精度如表1。量化单元是该设计中的一大核心模块，量化数据的精度决定了整个卷积运算中的数据精度。对于16位的定点数据，若保留最高精度可使用Q15 格式，即将数据放大215倍后用定点数表示，然而，若浮点数的有效数据超出该精度表示范围，即使该数据量化后带来的误差非常小，但将会损失全部有效数据。因此量化适用于有效精度在Q格式可表示最高精度范围内的数据，有效精度超出最高精度表示范围的极少数据将被舍弃。

表1 16位定点数的Q格式表示及精度

使用数据量化会引入额外的空间存储Q值，但是相比于存储原本的浮点数据，定点数与Q值所占的存储空间会明显降低，同时也降低了带宽需求。

为进一步解决量化过程中的误差问题，数据量化后使用了近似舍入方法对量化结果进行微调。

1.4 数据量化的舍入处理

在运算过程中，对量化后的数据进行数据舍入的方案也是至关重要的。例如定点数可以表示为[IL:FL]，分别对应着量化后定点数据的整数部分和小数部分，定点数据范围是[-2IL-1,2IL-1-2-FL]，其中IL、FL分别代表整数和小数位宽[19]。数据在量化过程中会涉及到数据截断，针对此情况本设计按照就近舍入原则，对量化后的定点数据进行分析，若定点数据中被截断部分最高位为1时，即被舍去部分的数值大于真实数值的0.5时，则将数据进行向上取整，小于0.5时将数据向下取整，保留整数部分即可。本设计中的数据舍入公式如式（4）：

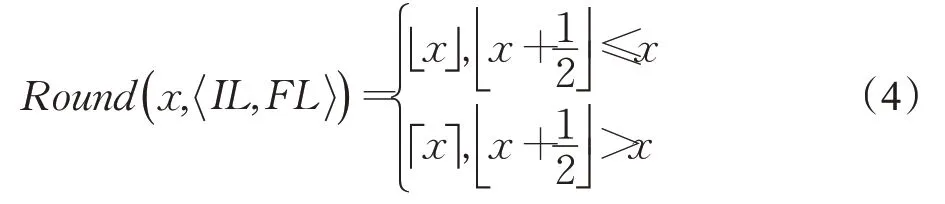
1.5 卷积运算单元结构

卷积神经网络（Convolutional Neural Network，CNN）主要包括输入层、卷积层、池化层、全连接层及输出层，其中最主要的运算为卷积运算，并且卷积层和全连接层包含的便是神经网络中最复杂、最耗时的运算[20]。在常用的网络模型中，如Alexnet 网络中包含的计算量达到上亿级，单是乘法运算就至少需要进行7 亿次。对于CNN的卷积层，每层的计算公式如式（5）：

其中，w是权重矩阵，b为偏置，f是激活函数，x是每一层的输入，Y是每一层的输出。

详细来说，其中主要卷积运算如下：

全部的n个输入样本为xi(i∈[1,n])，对应的内核权重为wi,j(i∈ [1,n],j∈[1,m])，相乘后可得到对应的输出w1,j x1+w2,j x2+…+wi,j xi+…+wn,j xn当浮点数量化为低精度的定点数后，根据输入的参数量化为使用Q格式的定点数据后，根据前后Q 值的变化，在计算完乘积之后，对结果进行截断与舍入处理，得出最终结果。

定点数据的乘法伪代码如下：

由伪代码可知，首先将两个输入数据进行相乘并将Q值相加，即结果中的小数部分位宽是输入数据的小数位宽累加和，此时可得出结果的数据范围，进而确定Q值。然后将超出位宽的低位部分进行截断，并进行舍入处理。在数据截断时会产生误差，但是由于截断的是数据最低位部分，即小数部分最低位，带来的误差很小。

而卷积中的加法运算原理与乘法不同。对于Q 值相同的定点数，直接进行运算，结果的Q 值与加数一致。然而，当两个Q 值不同的定点数进行运算时，需先将Q 较小的定点数进行移位处理，直至两加数Q 值一致，此时可直接执行加法运算。

在本设计中，原本需由浮点数执行的卷积运算转换为量化后的定点数据来执行，并将结果输出。

2 面向AI的动态定点量化单元架构

2.1 数据量化单元设计

从图2可以看出，首先根据输入数据可以得到结果的符号位。其次输入数据均为符合IEEE-754标准的浮点数，其中尾数部分给出了有效数字的位数，因而决定了浮点数的表示精度。而阶码指明小数点在数据中的位置，整数部分位宽便可确定，同时决定了浮点数的数据范围，因而确定了数据量化后最适合的Q 值，并做数据截断和数据舍入处理，进而使用Q格式完成参数的动态低精度定点量化，将量化后的结果输出。

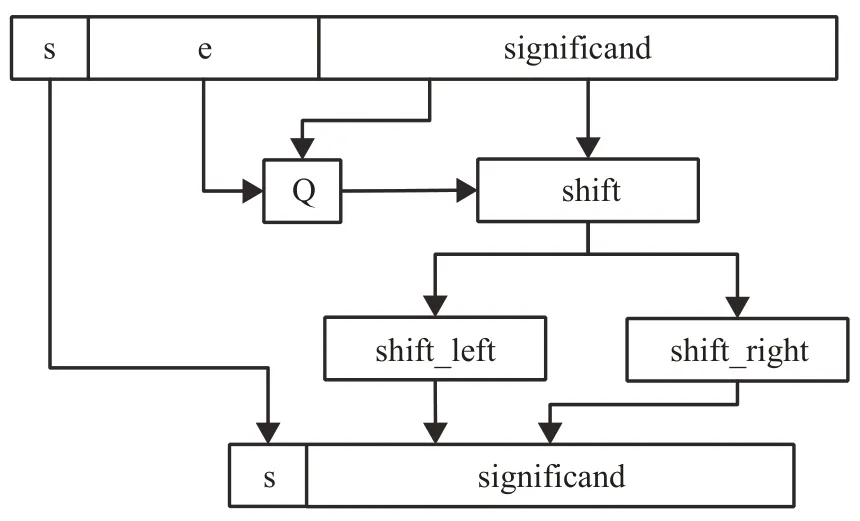
图2 动态低精度量化单元原理图

2.2 卷积运算单元架构设计

卷积网络中包含大量的卷积运算，从硬件层面讲，卷积运算分解下来即为连续的乘法和加法运算，其中乘法运算设计原理图如图3所示。

图3 乘法单元设计原理图

卷积层主要是由卷积核组成的，卷积核的作用主要是对神经网络中输入的特征图进行特征提取，执行对应参数的卷积运算[21-22]。在该部分的乘法单元设计中，将输入的两个参数送入乘法器中，首先可以根据输入数据得到乘法运算的结果，并确定符号位，然后根据两个输入数据的Q值及最小误差量化算法的思想，确定结果的Q 格式表示，对结果进行截断操作和舍入处理，与量化原理一致，得到最终的结果并输出。另外，针对卷积运算原理，提出并设计了矩阵运算单元，使数据并行执行乘法运算，可提升整体性能。

一般而言，针对神经网络的卷积运算加速的硬件设计，重点要考虑运算单元的并行性，如Alexnet 网络模型，共包括8 层，其中有5 层为卷积层。然而，对于在嵌入式设备来讲，完全实现卷积核之间与不同层神经网络的并行执行几乎是不可能的，本文主要针对卷积核内的并行化执行完成设计。图4为矩阵卷积运算设计架构，针对目前最常用的3×3 的卷积核设计了并行卷积运算架构，输入层是大小为13×13的神经元矩阵。经过量化后的结果按照一定顺序存入存储矩阵中，存储单元中高位为量化后的定点数，低位为对应的Q 值，之后从存储中取出对应的数据送至卷积运算单元的输入端，经边界填充最后可得到169个神经元输出。

图4 矩阵卷积运算单元设计架构

本设计可在单周期内从对应存储中取出量化后的数据送入卷积运算单元中，并行执行9 次乘法操作，随后将结果送入加法器，完成累加得到卷积结果。矩阵并行卷积运算单元共包含了9个乘法单元，使用空间换取时间的思想，在不增加核心逻辑资源的前提下，适当地将分时复用的电路进行复制，在保证控制面积的前提下更好地提升性能。本设计需耗时169 个时钟周期完成卷积运算，有效地提升了运算的效率。

2.3 量化卷积架构设计

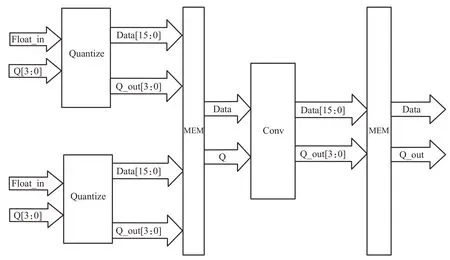
图5 量化卷积单元架构

量化卷积单元整体架构主要包括量化单元、存储模块以及可循环调用的并行卷积运算单元，量化卷积单元整体架构如图5。

首先将网络模型中的参数如神经元的输入、权重等进行动态低精度定点量化，即对数据进行预处理操作，然后分别存入对应的存储单元中。在执行卷积运算时，将数据分别从存储中取出，送入卷积运算单元，运算完成后将结果输出至存储并进行截断和舍入处理，循环调用卷积运算单元进行计算。

3 验证与分析

3.1 性能参数

本设计使用0.11 μm SMIC 工艺库进行综合，综合后的参数如表2所示。

表2 量化卷积单元参数表

本设计实现的功能为量化及卷积运算，综合后的量化与卷积单元面积为13 740门，功耗大小为0.992 5 mW。在本设计中针对运算加速做了相关的并行卷积运算单元设计，因此可有效提升卷积运算的性能，并且后期经过验证，本设计满足每个关键路径的时序要求。该性能参数表进一步证明本设计适合使用在对实时性有要求的嵌入式设备中。

3.2 结果准确性验证

本设计在FPGA 平台Stratix IV GX EP4SGX230进行验证，并完成了结果准确性对比。首先对原始的浮点数据不做量化处理，直接进行卷积运算，可得到当前结果的准确性。之后将原始的浮点数据分别进行16 bit、8 bit 的固定精度量化，在16 bit 情况下量化为Q14 格式的数据，8 bit情况下对权重和偏置量化为Q6格式数据，将输入输出量化为Q8格式数据，得出对应结果。最后验证本设计中动态多精度（Dynamic Multi-Precision，DMP）量化后卷积运算的结果准确性。结果准确性对比如表3。

表3 结果准确性对比

结果表明，直接使用浮点数据进行卷积运算的数据准确性最高，然而分别对数据进行16 bit和8 bit量化时发现，量化后的数据位宽越大，准确性越高。本设计中，对数据进行16 bit 多精度量化时，结果表明数据的准确性达到了97.96%，由于有个别数据精度特别低，量化过程中的数据截断会带来一定的误差，处于合理范围内，不影响网络推理的正常功能。

3.3 性能测试对比

本文还分别与使用RISC-V处理器（E203）[23]、Cortex M4与Matlab模拟执行卷积运算的时间进行对比。性能测试对比如表4。

表4 性能测试对比

在神经网络模型中，卷积层包含的运算占了总体的90%以上。针对神经网络Alexnet 模型进行性能验证，输入神经元数量为169 个，即输入数据的矩阵大小为13×13，卷积核大小为3×3，跨度为1，在不同平台模拟卷积运算。本设计中测试激励模拟了169 组随机数据进行验证。结果表明，编写C++代码软件模拟实现卷积运算，在CortexM4 开发板进行测试，参与运算的为浮点数。在100 MHz 时钟频率下测得执行时间为4.10 ms。由于RISC-V 处理器（E203）不支持浮点数据，模拟相同数量的INT32数据，经验证得出在100 MHz时钟下执行卷积运算时间为3.03 ms。在Matlab上调用卷积函数的方法，模拟相同数量的浮点数据执行卷积运算，测得执行时间为230 ms，本设计中模拟给出同等数量的浮点数据量化后的INT16数据，在100 MHz时钟下执行时间约为0.001 71 ms。经对比证明了该设计可有效提升卷积运算性能。

4 结束语

本文面向嵌入式平台提出一种卷积神经网络硬件加速器的设计与实现方法，采用卷积加速模块化和量化精度可配置的思想，针对神经网络推理加速设计了低精度动态量化单元与矩阵卷积运算架构，主要针对网络模型的卷积运算做加速。该设计使用16 位定点数据表示，内存占用量和带宽需求减半，数据精确度达到97.96%，对卷积网络的正常功能影响较小，与二进制设计相比，它具有更高的精度，性能相比软件实现有大幅提升，相比CortexM4 执行卷积运算提升了90%以上，可有效加快卷积运算执行速度，适用于提高神经网络在嵌入式平台的性能，为嵌入式卷积网络推理加速提供了方法。后续工作中还需继续深入研究，更好地实现卷积核间及层间的并行性，同时为移植到RISC-V 处理器中并完成指令集融合的协处理器做准备。