LCC-MMC型混合直流配电系统线路保护方案
2021-02-22王聪博毕天姝
贾 科 冯 涛 陈 淼 王聪博 毕天姝
(新能源电力系统国家重点实验室(华北电力大学) 北京 102206)
0 引言
电网换相换流器(Line Commutated Converter,LCC)已经在直流输电系统[1-2]和牵引配电系统[3]中成功应用,由于受端LCC换相失败[4]问题难以解决,而模块化多电平换流器(Modular Multilevel Converter,MMC)不存在换相失败问题[5],所以基于 LCC和MMC混合换流器的多端直流输配电可能成为未来直流电网的发展趋势。现有直流输电工程已经有混合换流器拓扑结构,给未来直流配电网的发展提供了理论基础。相比于已经建成的柔性直流配电系统[6],LCC-MMC型混合直流配电系统建设成本低,耐受暂态冲击电流能力较强,利用MMC控制电流双向流动的特点实现配网灵活性。然而直流故障发展迅速,可靠且有选择的保护原理亟待研究。
实际直流工程广泛采用闭锁换流器实现故障电流自清除和直流故障隔离[7],保护系统设备不受过电流的破坏。传统LCC直流工程主要通过移相方式[8],迅速将整流站触发延迟角移相到90°以上,使得整流站转变为逆变运行模式[9],向交流系统释放储存的能量,降低故障电流。MMC柔性直流配电工程通过向换流阀发送闭锁信号,闭锁换流器切断故障电流回路,隔离直流故障[10]。然而,故障后快速
闭锁换流器会导致提供给保护的有效故障信息减少、特征量单一,给传统直流线路保护的可靠性和选择性带来挑战。
现有直流系统线路保护根据故障检测的方式可以分为被动保护和主动保护。被动保护利用线路电气量的变化检测故障的发生[11]。文献[12]通过分析故障距离与故障电流之间的反比关系构建电流反时限保护,出口速度快,但故障电流波动影响保护的可靠性。文献[13]通过小波变换提取故障高频信息,结合系统高频阻抗模型构建高频距离保护。文献[14]采用低通滤波器处理线路两端测量电压和电流,利用线性分布的沿线电压求解沿线分布电容电流实现故障选极。文献[15]利用 Prony算法分析线路两端的电流固有频率,根据电流固有频率的差异性特征实现区内外故障识别,但是暂态衰减分量和换流器闭锁的干扰作用使得电流固有频率的提取存在一定的误差。
主动保护[16]通过主动控制电力电子变换器或注入附加信号检测故障的发生。文献[17]通过控制MMC子模块短时间的切出得到低压脉冲,利用低压脉冲在检测点和故障点之间传播的时间差计算故障距离实现快速保护,但是脉冲陡度过大和持续时间过长易造成正常运行时电压跌落。文献[18]通过在 DC-DC控制器中增加信号处理环节检测直流故障的发生,通过脉宽调制来控制变换器开关的开断并发送故障信息给保护。文献[19]通过投入附加装置,利用附加装置注入的特征信号确定故障区段,不受故障暂态量的影响,但是难以区分故障边界,需要采用额外装置,经济性受到制约。
因此,鉴于现有的被动保护存在故障边界模糊、保护性能受限于暂态分量波动和主动保护经济性较差的不足,本文在概述LCC-MMC型混合直流配电系统拓扑结构及其双极短路故障特征的基础上,提出一种基于 LCC注入故障电流的混合直流配电系统被动保护。利用LCC提供稳态故障电流,结合线路两端电流方向的差异识别区内外故障,解决了故障边界模糊的问题,基于LCC提供的稳态故障电流幅值比进行故障精确定位,无需注入附加信号,经济性好。最后在 PSCAD/EMTDC仿真平台上搭建LCC-MMC型混合直流配电系统仿真模型,验证了所提保护的有效性和可靠性。
1 LCC-MMC型直流配电系统故障特性
1.1 拓扑结构

图1 五端LCC-MMC型直流配电系统拓扑图Fig.1 Topology of five-terminal LCC-MMC type DC power distribution system

图2 LCC和CDSM-MMC结构简图Fig.2 Structure diagrams of LCC and CDS M-MMC
以现有的广州直流供电系统[20]、贵州五端柔性直流配电系统[21]和张北柔性直流配电系统[22]工程为例,在PSCAD上搭建的五端LCC-MMC型混合直流配电系统如图1所示。LCC采用12脉动换流器结构,由两个6脉动换流器组成,两个6脉动换流器交流侧的相位差30°,拓扑结构如图2a所示。MMC为具有故障电流自清除能力的钳位双子模块的模块化多电平换流器(Clamp Double Sub-Module based Module Multilevel Converter, CDSM-MMC),子模块拓扑结构如图2b所示。整流侧为LCC和CDSM-MMC1,逆变侧为 CDSM-MMC2。整流侧LCC采用定直流电流控制,CDSM-MMC1采用定直流电压控制。逆变侧CDSM-MMC2采用定有功功率控制。光伏和直流负荷经双有源全桥变换器(Dual Active Bridge, DAB)直流变压器与直流系统连接,控制方式为单移相控制。直流线路额定电压等级为±10kV,DAB通过占空比控制低压侧电压为750V,接地方式为交流侧高阻接地[23]。当直流线路发生双极短路故障后,换流器 CDSM-MMC1、CDSMMMC2、DAB1和DAB2闭锁,LCC采用不闭锁方式。在LCC定直流电流控制器限幅环节的作用下,触发延迟角趋于稳定,LCC注入的故障电流最终趋于稳定值,系统进入故障稳态阶段。由于故障后CDSM-MMC和DAB直流变压器闭锁,系统中负荷被切除,因此不考虑因电压跌落而无法满足负荷运行的问题。
LCC-MMC型混合直流配电系统的主电源通过LCC输出功率,其他辅助电源利用CDSM-MMC能够控制潮流双向流动的特点实现系统功率调节。在建的直流配电工程采用电缆线路供电,接地方式为高阻接地,单极接地故障和断线故障不会引起严重过电流,极间电压不会突变,因此本文的研究主要针对双极短路故障。
1.2 故障特征
双极短路故障发生后,CDSM-MMC和DAB直流电容迅速放电造成过电流,故障电流达到 IGBT耐受电流能力时,CDSM-MMC和DAB直流变压器闭锁[24],系统仅剩下LCC向故障点馈入故障电流,系统进入故障稳态阶段,LCC提供故障稳态电流。根据换流器的工作状态,整个故障过程可以分为两个部分:闭锁前和闭锁后[25]。闭锁前主要为换流器中直流电容放电过程[26],放电回路如图3所示。图中Ceq为故障时直流侧等值电容,Req和Leq为故障回路等值电阻和故障回路等值电感。

图3 电容放电回路Fig.3 Capacitor discharge circuit
实际系统中,电容放电回路的等值电阻Req远小于因此闭锁前直流电容的放电过程为一个二阶欠阻尼振荡衰减过程[27]。根据图3可以解析得到直流电容的放电电流为

式中,UdcN为直流线路额定电压;I0为故障时刻直流电流瞬时值。
当考虑平波电抗器和LCC直流出口滤波器时,图3中的等值电容Ceq和等值电感Leq将会改变,对应式(1)中的δ、ω0、ω和β变化,主要影响放电电流的时间常数和峰值。由于直流配电系统惯性环节少、阻尼小[28],故障发展迅速,平波电抗器使得保护装置有更多的时间来响应。
闭锁后阶段,LCC仍然依靠晶闸管两端交流线电压过零点自然换相,根据晶闸管的导通条件可知,LCC阀臂仍按照自然换相规则导通(详见图4a)。

图4 故障后阀臂导通和触发延迟角变化情况Fig.4 Schematic diagram of valve arms and firing angle change after a fault
随着LCC直流出口极间电压逐渐降低,LCC触发延迟角增大(详见图 4b),此时系统进入故障稳态阶段,LCC整流器直流出口电压为[29]
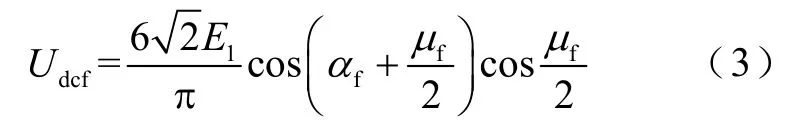
式中,E1为 LCC阀交流侧母线线电压;αf为故障稳态LCC触发延迟角;μf为故障稳态LCC换相重叠角。
根据上、下单桥的工作方式可知,在一个工频周期内,上、下单桥各换相6次,在交流侧相位相差30°的基础上,LCC直流出口电压脉动12次,如图5所示。
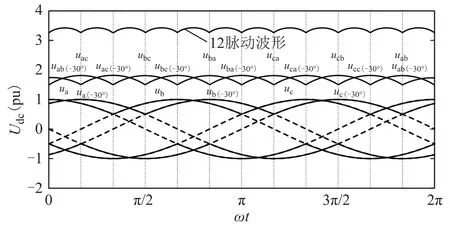
图5 LCC整流器直流出口电压波形Fig.5 DC outlet voltage waveforms of rectifier LCC
从图5可以看出,LCC注入的稳定故障电流含12m(m为正整数)次特征谐波。由于LCC直流出口一般装有特征谐波滤波器[30],因此在 CDSM-MMC和 DAB直流变压器闭锁后的故障稳态阶段,可以近似认为LCC注入到故障点的电流为直流电流,仅与故障回路电阻有关。结合式(3),闭锁后的稳态阶段,LCC注入的稳态故障电流为
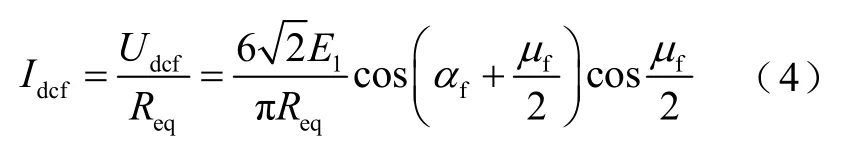
2 保护新原理
2.1 区内外故障识别
根据上面分析可知,CDSM-MMC和DAB直流变压器闭锁后,LCC经直流线路向故障点馈入故障电流,且为直流电流,故障回路示意图如图6所示。假定双极短路故障F发生在Line2上,故障电流回路有回路15(以隔离开关SW15为出发点,正负极线路与故障点形成回路)和回路12(以隔离开关SW12为出发点,正负极线路与故障点形成回路),p代表正极线路,n代表负极线路,Idcijp为隔离开关SWij处安装的保护测量的正极故障电流(i≠j,i=1,2,3,4,5,j=1,2,3,4,5),“+”和“-”分别代表电流方向为正和负。在此规定,由母线流向被保护线路为电流正方向。
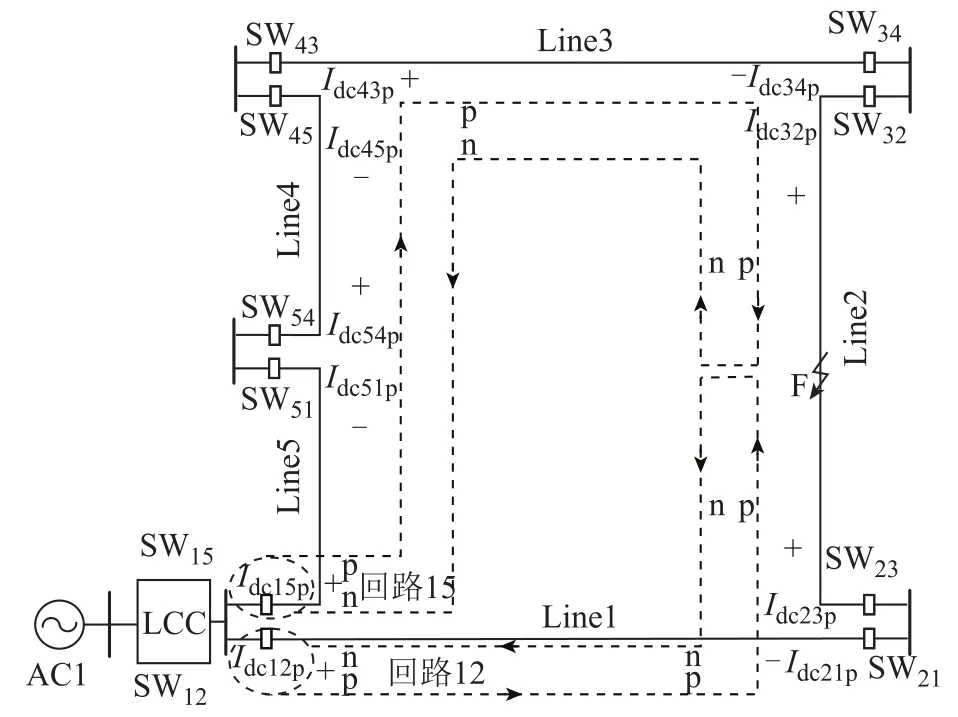
图6 闭锁后故障回路示意图Fig.6 Fault circuit diagram after blocking
定义k为线路两端正极故障电流比,表达式为

根据图6可知,故障线路Line2两端正极电流方向均为正方向,非故障线路两端正极电流大小相等,方向相反。因此故障线路两端正极电流比值大于零,非故障线路两端正极电流比值为-1。因此,可得故障识别判据为

当线路两端正极电流比值满足式(6)时,认为发生区内故障;当线路两端正极电流比值不满足式(6)时,则认为发生区外故障。
2.2 故障定位
结合图6,从LCC端口出发,LCC-MMC型直流配电系统故障回路各级线路阻抗均与 LCC端口串联,故障距离简要示意图如图 7所示。图中,x2为故障回路15的故障距离,x1为故障回路12的故障距离,x为环网线路总长度,R15、R12分别为故障回路15和故障回路12的单极线路总电阻,Rf为过渡电阻,Udcf为故障后LCC出口极间电压,Uf为故障点极间电压。
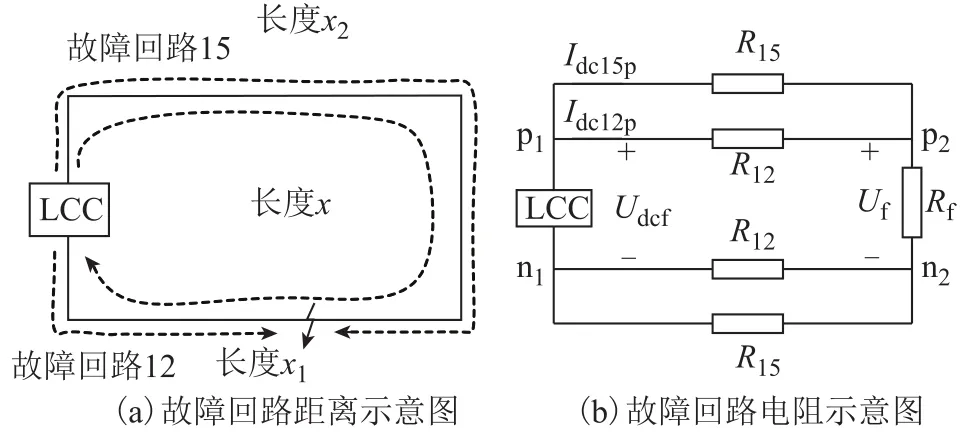
图7 故障电流回路简图Fig.7 Diagram of fault current loop
根据环网拓扑结构可知,整个LCC-MMC型直流配电网的线路总长度x已知。根据图7a可知,故障回路15和故障回路12的故障距离与系统环网总长度的关系为

根据图7b可知,故障回路15和故障回路12的正极线路故障电流为
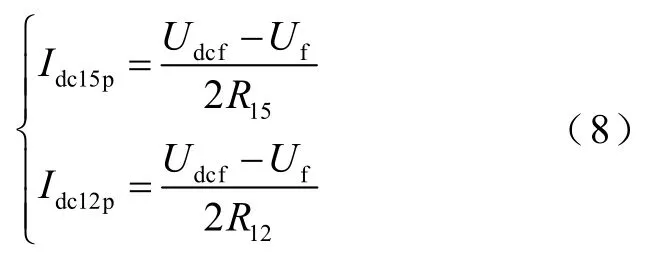
根据图6可知,故障回路15和故障回路12均是直流线路的简单串联,因此故障回路15中故障线路正极电流Idc32p等于LCC出口正极电流Idc15p,故障回路12中故障线路正极电流Idc23p等于LCC出口正极电流Idc12p。于是故障线路Line2的正极故障电流比k为

结合式(8)和式(9),可以推出正极故障电流比k为

由式(10)可知,k与过渡电阻Rf无关,仅与故障回路15和故障回路12的总回路电阻R15和R12有关。
由于LCC-MMC型混合直流配电系统线路阻抗均匀分布,因此可以得出

式中,r0为线路单位长度电阻值。
结合式(10)和式(11)有

联立式(7)和式(12)有

由式(13)可以求解得出故障距离x1为

2.3 保护流程
本文所提保护方案如图8所示,该保护方案由保护启动、区内外故障识别和故障定位三部分组成。保护启动过程配置di/dt作为启动判据。保护装置启动后,当故障电流达到 IGBT耐流能力时,闭锁CDSM-MMC和DAB直流变压器,利用线路两端故障电流比k实现区内外故障识别。工业换流器动态调节时间一般为30ms[31],结合大量仿真数据,本文设置硬延时t=30ms确保故障进入稳态阶段,结合式(14),利用稳态数据实现故障精确定位。

图8 保护方案流程Fig.8 Flow chart of protection scheme
3 仿真验证
利用 PSCAD/EMTDC电磁暂态仿真平台搭建如图1所示LCC-MMC型混合直流配电系统的仿真模型。直流电缆采用分布参数模型,电缆长度均为3.5km,单位电阻为0.066 9Ω/km,单位电感为0.685 7mH/km,单位单极对地电容为 0.35μF/km,具体参数详见附表1和附表2,保护装置采样频率为10kHz。
3.1 故障识别与检测
以 Line1为例,分析区内故障和区外故障时Line1两端正极故障电流比k的取值情况,仿真结果如图 9所示,故障发生时刻为 0.5s。LCC-MMC型混合直流配电系统发生双极短路故障后,闭锁CDSM-MMC和 DAB直流变压器,LCC注入的故障电流回路为RL回路,从图9a可以看出,故障发生12ms后,系统进入故障稳态状态,此时Line2两端正极电流比k为稳定值,表明故障稳态电流为稳定的直流电流。
根据图9a可以看出,当发生区内故障时,Line2两端正极电流比k>0,满足故障识别判据(详见式(6))。从图9b可以看出,当区外故障发生时,Line2两端正极电流比k=-1<0,不满足故障识别判据(详见式(6))。因此,本文提出的故障识别判据可以准确识别区内外故障,无需进行数值整定,就能可靠区分故障边界。

图9 区内外故障识别Fig.9 Fault identification in and outside the area
3.2 故障定位验证
3.2.1 故障定位的性能
分别以 Line1、Line2、Line3、Line4和 Line5不同位置故障为例分析所提保护方案进行故障定位的性能,仿真结果如图10所示。故障距离(故障位置)均为式(14)中的x1,即故障点到 LCC直流出口SW12的故障距离。从图10可以看出,双极短路故障发生在不同线路不同位置时,利用 CDSM-MMC和DAB直流变压器闭锁后20~30ms内LCC注入的稳态故障电流得到的故障定位结果趋于稳定,稳态误差均小于1%。

图10 不同故障位置定位仿真结果Fig.10 Fault location simulation results of different fault positions
统计不同故障位置定位的仿真结果见表 1。表中位置系数为某一线路上的故障点到该线路首端的距离占该线路长度的百分比,计算距离为利用所提保护算法求解得到的故障距离。

表1 不同位置故障定位仿真结果Tab.1 Fault location results at different fault positions

(续)
根据表1中结果可以看出,在LCC-MMC型混合直流配电系统中,Line1、Line2、Line3、Line4和Line5分别设置故障位置系数 10%、42.9%、57.1%和90%的双极短路故障时,利用所提的保护算法得到的故障距离最大误差不超过1%。
3.2.2 含过渡电阻分析
前文已研究非金属性双极短路故障时的保护算法,根据分析可知,过渡电阻位于故障回路15和故障回路 12之间,在求解线路两端正极电流比k时,过渡电阻作为两个故障回路的共有部分从算法上被消掉,因此过渡电阻不影响所提保护方案的定位效果。但是当过渡电阻较大时,故障回路 12和故障回路 15的故障电流很小,导致故障定位的结果误差偏大。本文设置过渡电阻为5Ω、20Ω和40Ω时的故障定位结果见表2。从表2中可以看出,当过渡电阻分别为 5Ω和 20Ω时,不同线路故障时保护算法定位结果准确可靠,误差小于 1%。当过渡电阻为 40Ω时,除 Line1故障位置 0.35km时误差为1.343%外,其余线路误差均小于1%,定位结果准确可靠。

表2 不同位置非金属性故障定位结果Tab.2 Non-metallic fault location results at different fault positions

(续)
3.2.3 含分布式电容分析
线路分布式电容对故障电流的影响很大,本文采用分布参数模型分析线路分布式电容对所提保护算法的影响,仿真结果如图11所示。
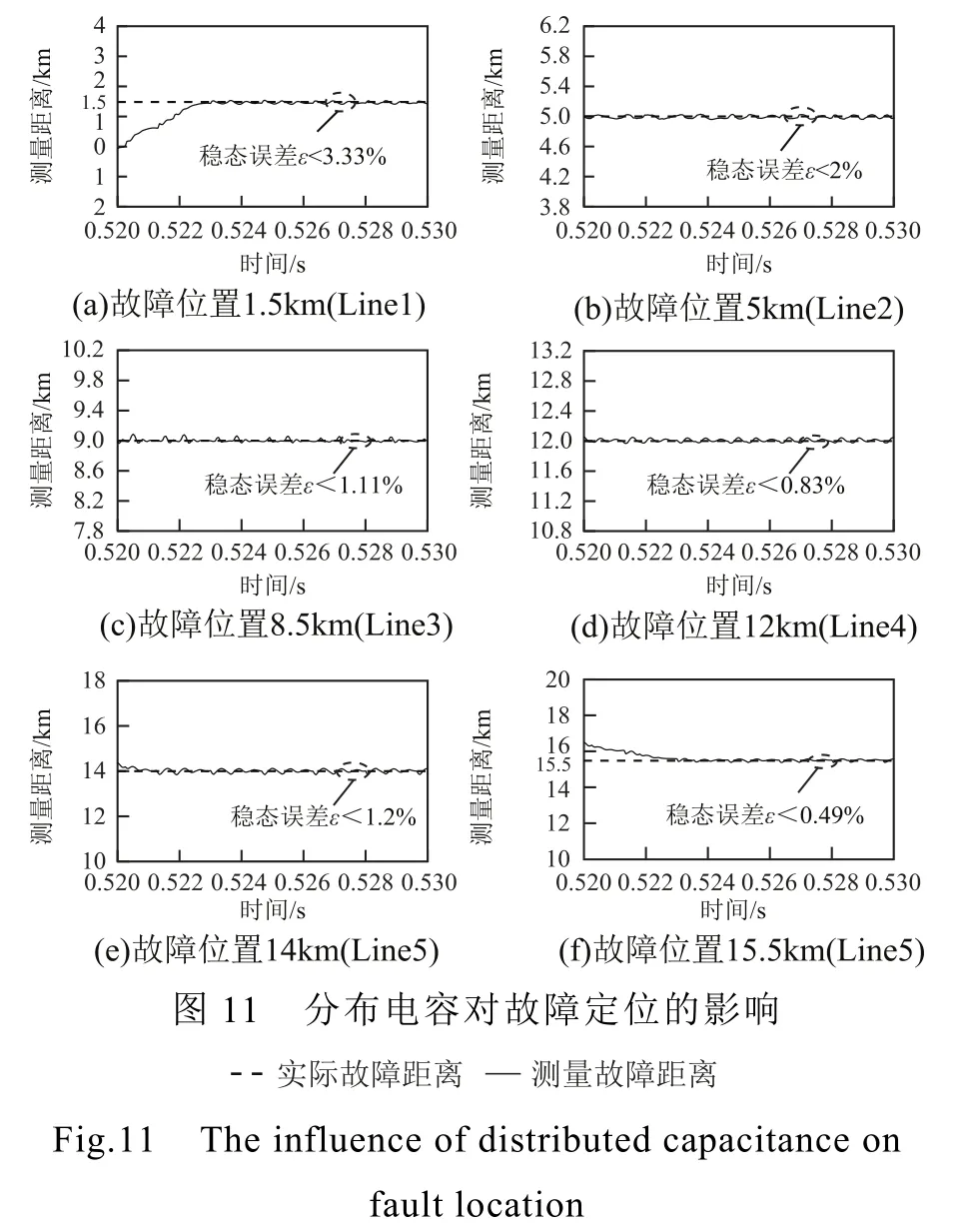
线路分布式电容的故障电流特性会导致 LCC注入的稳态故障电流波动。从图11可以看出,不同线路故障时,故障定位结果均在实际故障距离点上下波动,稳态误差小于5%,所提保护算法能够准确定位故障位置。
3.2.4 含噪声分析
实际工程中的采样数据往往受到电磁干扰和量测误差的影响,通常在采样数据中叠加高斯白噪声来模拟这些影响[32]。本文分别设置信噪比(Signal to Noise Ratio, SNR)为50dB、40dB、30dB和20dB,以 Line2故障位置系数 42.9%为例,通过仿真分析不同信噪比对所提保护算法的影响。仿真结果如图12所示。噪声主要影响 LCC注入的稳态故障电流波动,由于噪声能量相对稳态的故障电流较低,因此一定程度的噪声对故障定位结果的影响较小。从图12可以看出,当SNR=50dB和40dB时,噪声造成定位结果波动的影响较小,故障定位结果误差小于5%,所提保护算法定位结果可靠;当SNR=30dB和 20dB时,噪声对保护算法定位结果的影响显著增加,定位误差较大,定位结果不可靠。

4 结论
基于 CDSM-MMC和 DAB直流变压器闭锁后LCC提供稳态故障电流的特点,本文提出一种基于LCC注入的混合直流配电系统双极短路故障保护原理,并进行了仿真验证。所提保护原理满足直流配电系统保护选择性和可靠性的要求,保护原理简单,计算量小,受过渡电阻和分布式电容影响小,与传统保护方案相比,无需数值整定,经济性好,不需解列环网系统即可实现故障边界的区分,所提保护方案定位结果精确可靠,有利于故障后快速检修和供电恢复。然而,本文所研究的保护方案缺乏速动性,未来需要进一步研究缩短暂态过程的方法,实现快速的保护。
附 录

附表1 换流器相关参数App.Tab.1 Related parameters of converters
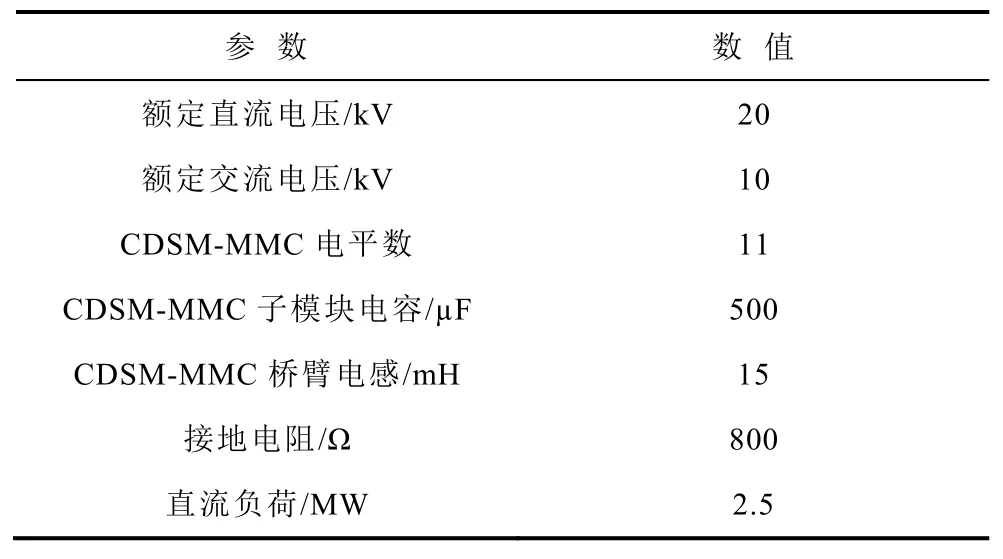
附表2 直流配电网相关参数App.Tab.2 Related parameters of dc distribution network
