考虑电氢耦合的混合储能微电网容量配置优化

2021-02-22赵淑丹蒲雨辰陈维荣

电工技术学报 2021年3期

李奇赵淑丹蒲雨辰陈维荣于瑾

（1. 西南交通大学电气工程学院成都 611756 2. 国网山东省电力公司烟台供电公司烟台 264001）

0 引言

随着经济的快速发展，能源不足危机和环境污染问题在全球范围内已经引起了广泛的关注，进行能源结构改革迫在眉睫。与传统的化石能源发电相比，以风力发电和光伏发电技术为主的分布式发电技术具有高效性和环境友好性[1-2]，因此，分布式发电技术被广泛使用。为解决分布式电源并网问题，科学家们提出了微电网的概念[3-4]。

微电网内各设备的容量合理配置是微电网规划设计阶段的重要内容，对保证系统安全稳定运行、减少投资成本等方面具有重要的指导意义。近年来，对于微电网容量配置已有很多研究。文献[5]提出了一种基于灵敏度分析的微电网容量配置方法，考虑风/光/柴/储灵敏度与微电网总成本的关系，得到容量优化的最优配置方案。文献[6]考虑了分布式电源、储能装备和负荷的不同特性，提出了一种微电网混合储能容量优化配置方案，减小了日电负荷的峰谷差。文献[7]以实现多类型能源的协同优化和微能源的经济效益最优为出发点，综合考虑分布式发电机组的出力特性、投资效益及碳减排政策，完成了储能系统的容量优化配置。文献[8]基于海岛用水需求及海水淡化系统的特点，综合考虑运行经济性及环境效益，提出了风/光/柴/蓄及海水淡化负荷的微电网容量优化配置模型，并验证了所提策略的有效性。

通过以上分析发现，目前针对微电网容量优化配置的研究大多以风光发电、柴油发电机和蓄电池间的协调配合为主，针对氢储能系统并入微电网的研究相对薄弱。但是氢能具有清洁、高效、能量密度大等优势。电能氢能协调配合，能够提高能源利用率，实现能量梯级利用。因此，考虑电氢耦合的混合储能微电网的容量优化配置研究具有重要意义。文献[9]提出一种含氢储能和蓄电池混合储能系统的风/光/储微电网，建立容量配置优化模型，并基于HOMER Pro软件设计算例进行求解。文献[10]基于快速估计方法，考虑含氢储能系统的微电网中电、氢储能系统不同的响应时间，根据实际天气、负载情况对微网系统进行容量优化配置。文献[11]对于含有单一电解制氢系统的孤岛微电网系统进行了基于碳排放和限制最大容量上的优化。

基于微网容量配置问题，粒子群优化算法（Particle Swarm optimization, PSO）具有鲁棒性好、寻优速度快、效率高等优点，且在求解不连续、不可微的非线性优化问题时具有强大优势。文献[12]利用粒子群算法求解微电网净收益最优时的储能系统容量，文献[13]建立了混合储能系统容量配置优化模型，利用改进粒子群算法对算例进行求解。文献[14]以环境效益及有功损耗最优为目标，利用改进粒子群算法对目标函数进行求解。文献[15]在综合考虑经济性、供电可靠性、环境效益等评价指标基础上，建立不同导向的微电网容量配置优化模型，采用自适应权重粒子群算法进行求解，得到了不同模型下的最优解，验证了所提方法的正确性。在求解过程中，所设参数直接影响算法的最终结果。

上述研究多以微电网系统运营成本或净收益为优化目标，未计及系统的稳定性，而以经济性最优时的容量配置结果不能完全平抑母线功率及电压波动，缺乏对微网系统供电可靠性的评估。在此基础上，本文提出将由电解槽-储氢罐-燃料电池组成的氢储能系统应用于孤岛直流微电网的容量优化配置问题。首先，建立微电网内各分布式能源的数学模型，包含电储能系统模型和氢储能系统模型。然后，提出一种以微电网系统经济性和供电可靠性为目标，以单位电量成本、负载失电率和能量过剩率作为评估指标的微网容量优化配置方法。通过控制系统内各储能装置的工作状态，决定各微源的出力顺序，再使用加权法将多目标问题转换为单目标问题。最后，选取某地区一年内的光照及负荷数据进行算例分析，采用粒子群优化算法求解模型，并对比分析不同优化算法、权重系数对优化结果的影响。采用RT-LAB半实物仿真平台将配置结果在实际情况下进行了实验验证。

1 微电网的系统结构及数学模型

1.1 系统结构

本文所研究的考虑电氢耦合的混合储能微电网的系统结构如图1所示，主要由光伏阵列、蓄电池、燃料电池、电解槽、储氢罐、负荷及DC-DC变换器等元件组成。储能系统包括以蓄电池为主的电储能系统和以燃料电池、电解槽、储氢罐为主的氢储能系统，其中燃料电池与电解槽为电氢耦合元件。

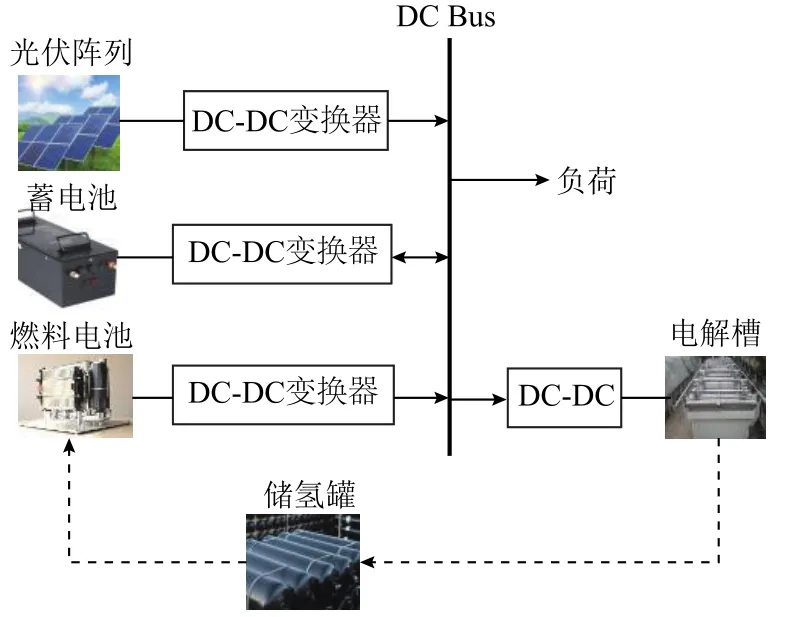
图1 微电网系统结构Fig.1 Microgrid structure

1.2 数学模型

1.2.1 光伏电池模型

为了减小误差，提高所建模型的准确性，光伏电池的实际输出功率需要同时考虑实际光照强度和实际环境温度，因此光伏电池的实际输出功率表示为

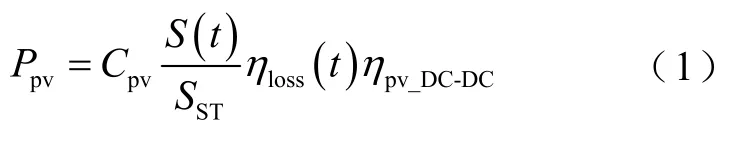
式中，Cpv为光伏电池的额定输出功率；S(t)和SST分别为t时刻光照强度和标准光照强度；ηpv_DC-DC为光伏电池的DC-DC变换器效率，本文取90%；ηloss为由于温度升高光伏电池产生的功率损耗，可表示为

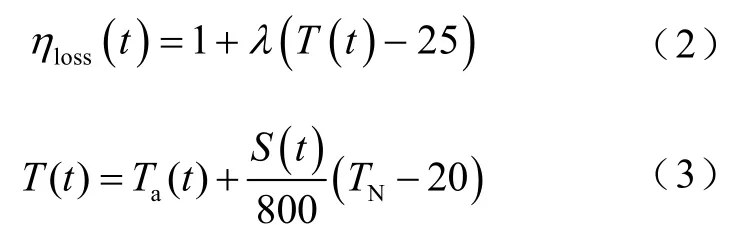
式中，λ为温度系数，本文取λ=0.004 85/℃；T(t)为工作温度，可由环境温度与光照强度进行估算；Ta(t)为实际环境温度；TN为标准工作温度，取为25℃。设计寿命为20年。

1.2.2 蓄电池模型

蓄电池可以有效平抑微电网内负载需求突变引起的波动。当光伏输出功率大于负荷需求功率时，蓄电池处于充电状态；反之，蓄电池处于放电状态。其特性如下。

蓄电池充电时

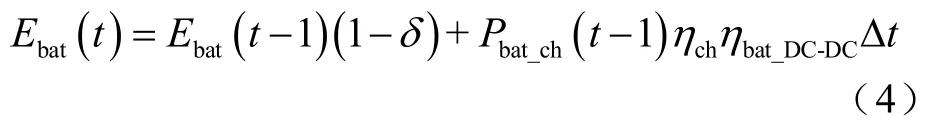
蓄电池放电时

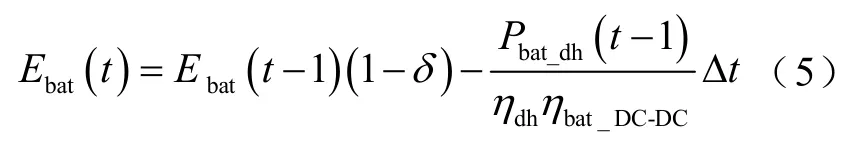
式中，Ebat(t)为t时刻蓄电池储存的能量；δ为蓄电池自放电率，根据相关实验结果，本文取0.46%/天；Pbat_ch、Pbat_dh分别为充、放电功率；ηch、ηdh分别为蓄电池的充电和放电效率，本文均取 90%；ηbat_DC-DC为蓄电池的DC-DC变换器效率，本文取90%；Δt为时间步长，本文取1h。

在系统运行过程中，蓄电池经历充电和放电过程受其荷电状态（SOCmin＜SOC＜SOCmax）的约束，蓄电池的最大充、放电功率可分别表示为

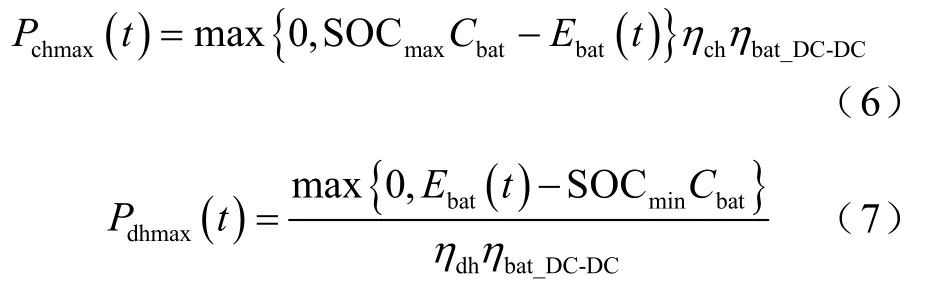
式中，SOCmax、SOCmin分别为蓄电池荷电状态的上、下限；Cbat为蓄电池的容量。

1.2.3 电解槽-储氢罐-燃料电池模型

本文所建电解槽-储氢罐-燃料电池模型与蓄电池储能的作用相同，即在光伏资源充足条件下，电解槽利用多余电能电解水制氢，并将氢气储存在储氢罐中；当光伏资源不足时，燃料电池以储氢罐中的氢气为燃料进行发电，满足电负荷需求。

电解槽能够将水电解为氢气和氧气。其输出功率可表示为

式中，Pel为电解槽的输入功率；ηel为电解槽的效率，本文取为60% 。

燃料电池模型为质子交换膜燃料电池（Proton Exchange Membrane Fuel Cell, PEMFC），以氢气和氧气作为燃料，将化学能转换为电能储存起来，其输出功率为

式中，Ptank-fc为储氢罐输入到燃料电池中的功率；ηfc为燃料电池的工作效率。

储氢罐用来储存电解水产生的氢气，也可以为燃料电池提供氢气，提高系统的灵活性，其储能的数学模型可表示为

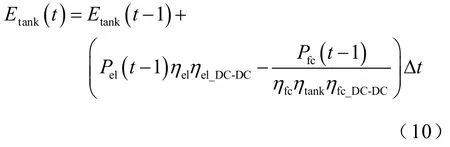
式中，Etank(t)为t时刻储氢罐储存的能量；ηel_DC-DC、ηfc_DC-DC分别为电解槽和燃料电池的工作效率，本文均取 90%；ηtank为储氢罐的工作效率，本文取ηtank=50%。

电解槽的最大输入功率与燃料电池的最大输出功率受其容量与储氢罐剩余储能容量的限制，可分别表示为

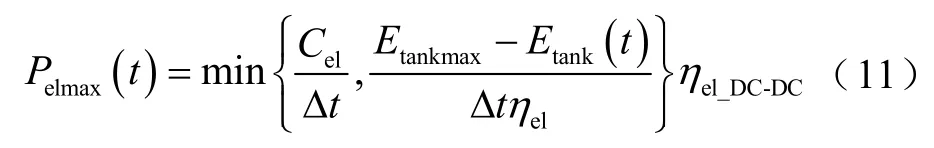
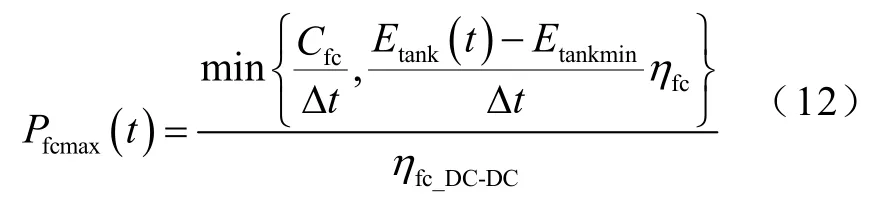
式中，Cel、Cfc分别为电解槽及燃料电池的容量；Etankmax、Etankmin分别为储氢罐储能容量的上、下限；Ctank为储氢罐容量；本文中取Etankmax=0.8Ctank，Etankmin=0.2Ctank。

2 微电网优化配置模型

2.1 目标函数

本文研究的微电网系统主要包括光伏阵列、电储能系统、氢储能系统及负荷。因此容量配置的对象，即优化变量，为光伏阵列、蓄电池、电解槽和燃料电池的容量。配置围绕微电网系统经济性和供电可靠性两个目标进行，供电可靠性由负载失电率和能量过剩率两个指标表征。

2.1.1 经济性

本文以微电网系统的单位电量成本 LCE作为经济性目标函数。该目标函数可表示为

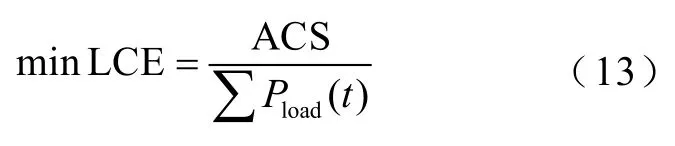
式中，∑Pload(t)为年负荷消耗能量；ACS为系统等年值投资费用 (Annualized Cost of System, ACS)，可以表示为

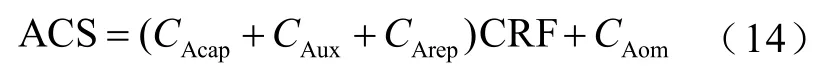
式中，CAcap为年主设备投资费用，包括光伏阵列、蓄电池、燃料电池、电解槽和储氢罐等设备；CAux为年辅助设备投资费用；CArep为年重置成本；CAom为年运行维护成本；CRF为资金回收系数（Capital Recovery Factor, CRF），其表达式为

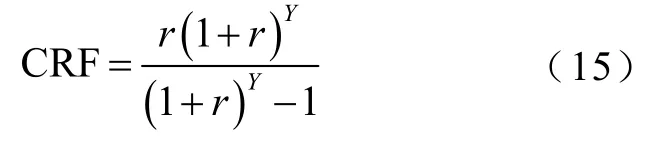
式中，r为实际年利率，本文取4%；Y为项目设计年限，即微电网寿命周期。

主设备购买成本与设备型号、额定容量等因素有关，光伏电池、燃料电池的购买成本取决于其额定功率，因此，主设备投资成本可表示为

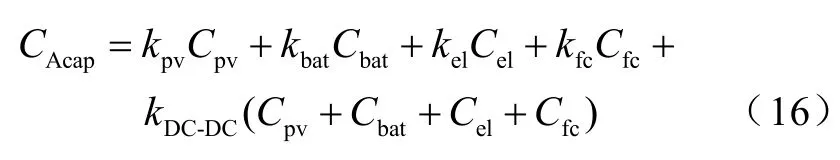
式中，kpv、kbat、kel、kfc、kDC-DC分别为光伏阵列、蓄电池、电解槽、燃料电池和DC-DC变换器设备购买单价；Cpv、Cbat、Cel、Cfc分别为光伏阵列、蓄电池、电解槽和燃料电池的容量。

由文献[16]分析可知，辅助投资成本与主设备投资成本成正比例关系，表达式为

式中，kaux为比例系数，本文取0.1。

在微电网寿命周期内，光伏阵列寿命较长，一般不需要更换；而蓄电池和燃料电池的相对寿命较短，需要进行部分或整体的替换，因此需要考虑重置成本。

年运行维护费用包括燃料费用和设备维护费用，它与设备购买成本成比例，即

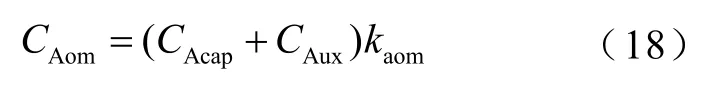
式中，kaom为从设备购买成本转换为运维成本的因子，本文取0.01。

2.1.2 负载失电率

负载失电率 LPSP是系统缺额功率和负荷需求功率的比率[17]。孤岛微电网由于未连接到电网，其负荷需求全部由系统自身提供。因此，负载失电率通常用于表征孤岛微电网的可靠性。其表达式为

式中，Punmet(t)为t时刻的缺额功率；Pload(t)为t时刻的系统负荷。

2.1.3 能量过剩率

当光伏出力与负荷消耗功率不匹配时，由于输出功率的限制，储能系统不能完全吸收光伏发电系统的多余能量，系统的能量过剩率定义为系统的总盈余能量与系统的负荷需求功率的比率，其表达式为

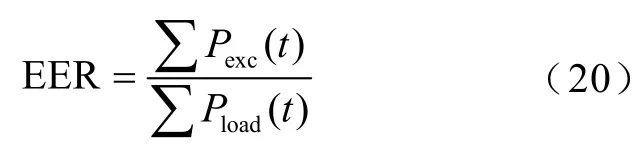
式中，Pexc(t)为t时刻的盈余功率。

2.2 约束条件

（1）功率平衡约束

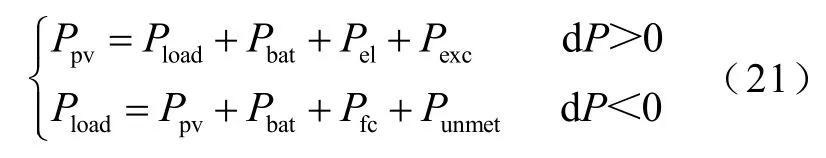
（2）充放电深度约束

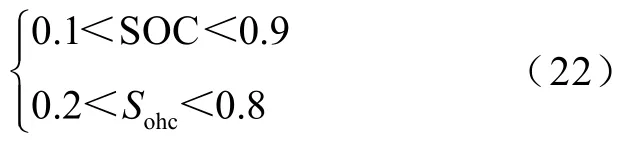
式中，SOC为蓄电池的荷电状态；为便于研究储氢罐的存储状态，本文引入等效荷电状态Sohc[18]，即

式中，psto为储氢罐内的压强；pN为储氢罐最大压强。

（3）各装置容量约束

本文以各装置容量为优化变量，考虑系统优化配置方案的合理性，需要对微网内分布式电源做出装机容量约束，自变量约束范围见式（24），同时规定储氢罐最大容量。

3 微电网的运行控制策略与模型求解方法

3.1 运行控制策略

微电网的运行控制策略决定着微电网中各微源的出力顺序，直接影响蓄电池和氢储能系统的工作情况，从而影响配置方案的优劣。本文所提的微电网系统运行策略流程如图2所示。当光伏功率大于负荷功率时，多余的能量首先给蓄电池充电，剩余能量通过电解槽转换为化学能并储存在储氢罐中。当光伏功率小于负荷功率时，由蓄电池优先工作，释放电能以补充系统缺额功率，再由燃料电池发电补充缺额功率。

对应图 2中的Pchmax、Pdhmax、Pelmax、Pfcmax分别按照式（6）、式（7）、式（11）、式（12）计算，对应运行控制策略中的字母 A～F表示系统在对应时间段内的工作状态，分别如下：

A：在满足负荷需求功率后，光伏发电系统的剩余功率全部用于对蓄电池充电。

B：在满足负荷需求功率后，光伏发电系统的剩余功率一部分用于对蓄电池充电，另一部分则通过电解槽转换为氢气储存起来。

C：光伏出力在满足负荷需求功率后，对蓄电池充电直至饱和，再为电解槽提供充足能量，过剩功率记为Pexc(t)。

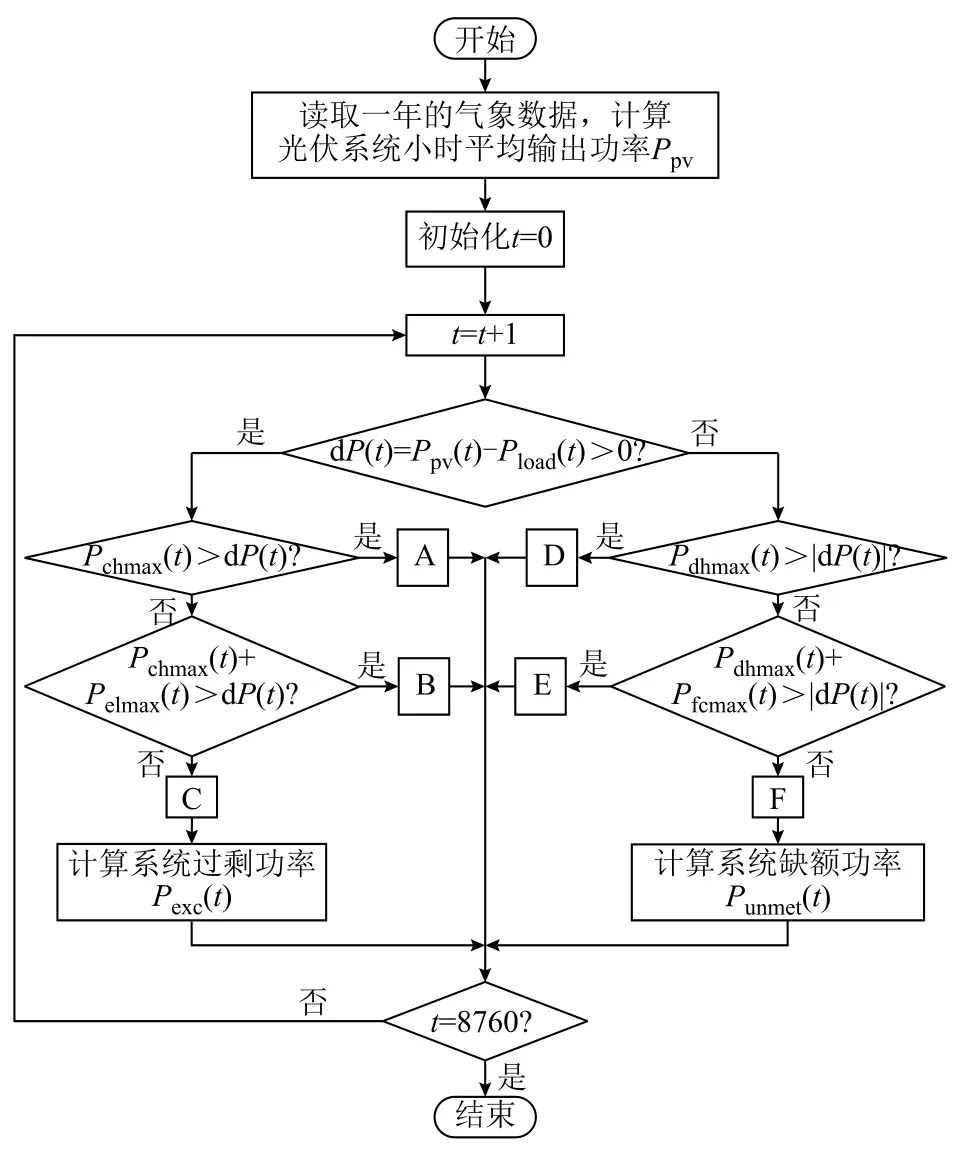
图2 运行控制策略流程Fig.2 Operation management strategy flow chart

D：系统缺额功率全部由蓄电池提供。

E：蓄电池充分放电为系统提供一部分缺额功率，剩余部分由燃料电池发电提供。

F：蓄电池充分放电和燃料电池完全发电为系统补充部分功率，后续缺额功率记为Punmet(t)。

3.2 模型求解方法

以微电网中光伏阵列、蓄电池、电解槽和燃料电池的容量为优化变量，建立优化配置模型。考虑微电网优化配置是一个非线性多目标问题，难以得到全局最优解，因此本文采用粒子群优化算法进行求解。PSO算法具有鲁棒性好、计算效率高、简单易实现的优点。结合本文研究对象及运行控制策略，利用 PSO算法进行微电网优化配置的基本步骤如图3所示，首先对系统优化变量进行初始化，包括粒子群的规模、粒子的位置与速度，然后根据一年内的气象数据求出系统中光伏每小时的出力。结合负载数据，完成全年系统仿真，得到光伏年发电量、系统年缺电量和年过剩电量，计算负载失电率和能量过剩率，最后根据年投资成本、运行维护成本求解目标函数，并迭代优化得到最优解。

以微电网系统单位电量成本、负载失电率和能量过剩率为优化目标，通过计算三个目标函数的理想值，然后再求各目标函数值与理想值的相对误差的二次方和，得到加权后的单目标函数为

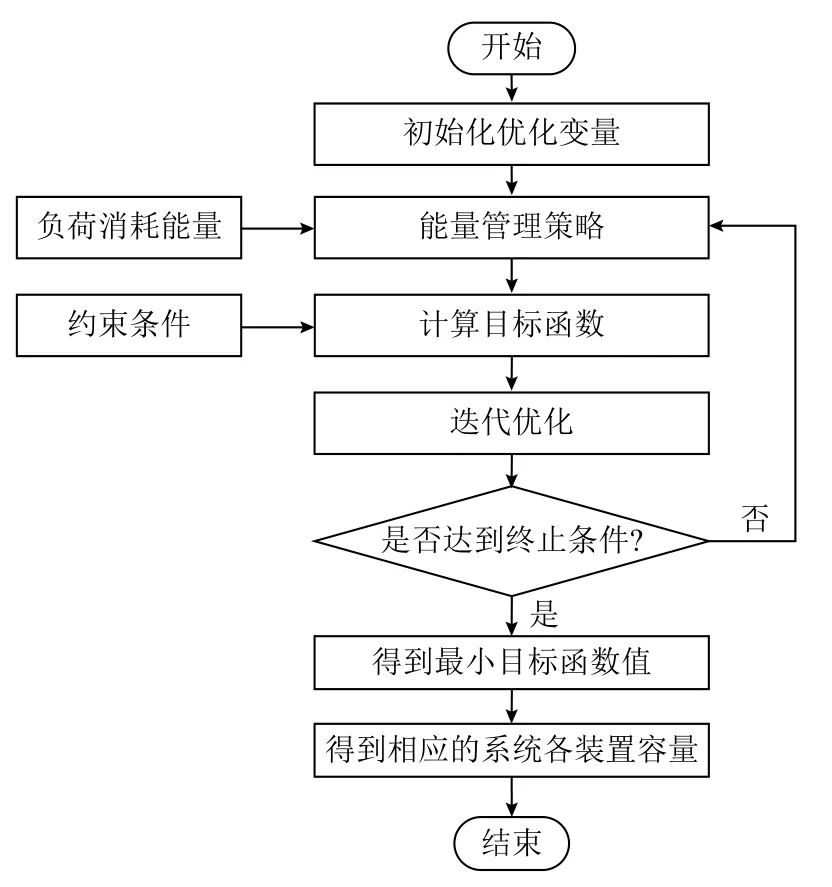
图3 电氢孤岛微电网优化配置流程Fig.3 Optimized configuration flow of electrohydrogen island microgrid

式中，F为目标函数；LCEdesired、LPSPdesired、EERdesired分别为各目标函数的理想值；w1、w2、w3为加权因子。

4 算例分析

4.1 典型仿真场景

根据上文建立的容量优化配置模型，选取西北某地区的全年光照数据和负荷数据作为系统输入数据，仿真步长设置为1h，共计8 760组测量数据。其中，年平均光照强度为 206.79kW/m2，年负荷量为 1 810 402.84kW⋅h，负荷日平均值为 206.67kW。具体光照资源年度分布和每小时负荷需求功率如图4和图5所示。

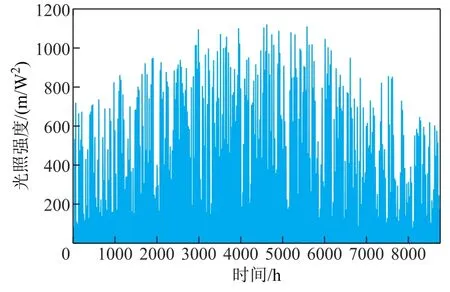
图4 光照资源年度分布Fig.4 Annual distribution map of light resource

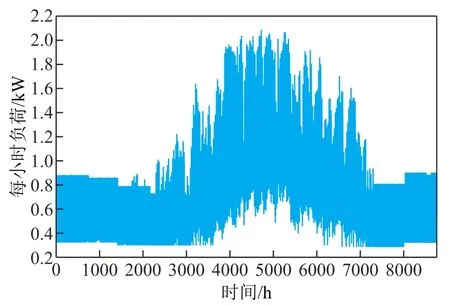
图5 每小时负荷需求功率Fig.5 Diagram of hourly load demand power

4.2 参数设置

本文设定微电网系统的寿命周期为20年，在此期间，蓄电池需更换5次，电解槽、燃料电池及储氢罐都需要更换1次。同时通过仿真计算，得到各目标函数的理想值。微电网部分储能参数见表1。

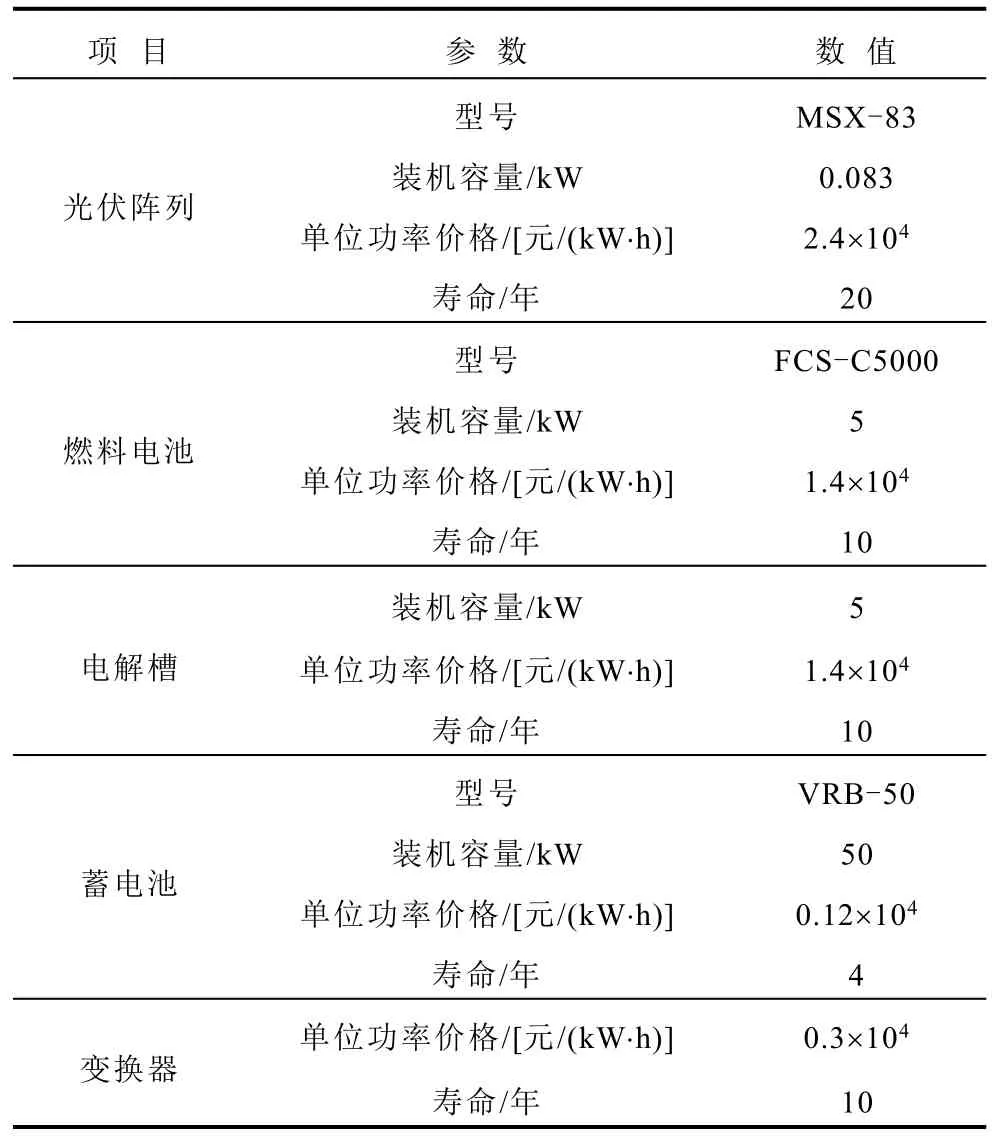
表1 电源及储能参数Tab.1 Parameters of power supply and energy storage

通过Matlab仿真计算，得到各目标函数的理想值。

表2 微电网系统其他参数Tab.2 Other parameters of microgrid system

4.3 优化算法对容量优化配置结果影响

根据本文所提容量优化配置方法，设置粒子群数量为30，迭代次数为100次，同时采用回溯搜索算法[19]（Backtracking Search Algorithm, BSA）作为对比，得到两种优化算法下的配置方案及目标函数值，见表3和表4。

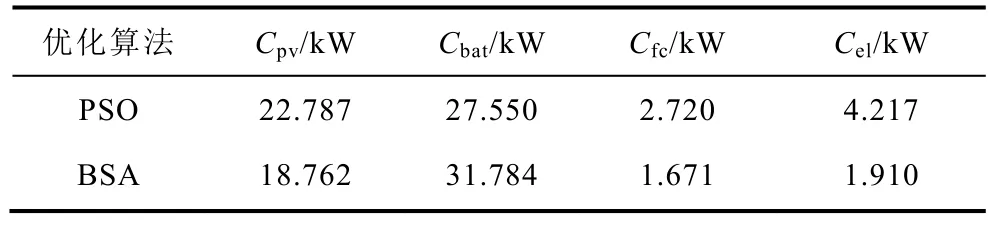
表3 优化配置结果Tab.3 Optimized configuration results

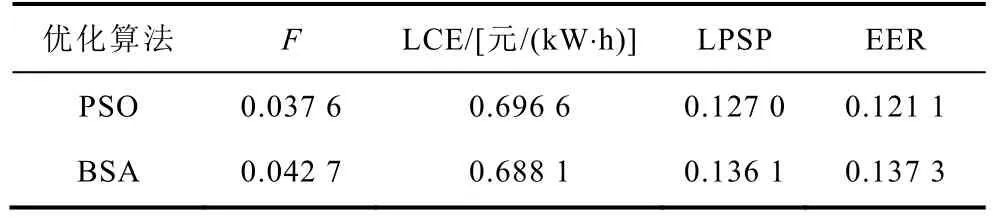
表4 优化配置目标函数值Tab.4 Objective function value for optimal configuration

由以上结果可以看出，两种优化算法得到的三个目标函数均接近理想值，由此产生的容量配置方案能够满足用户的需求。同时PSO算法优化得到的单位电量成本略高于BSA算法，但负载失电率和能量过剩率均低于 BSA算法得到的结果。因此采用PSO算法对考虑电氢耦合的混合储能孤岛微电网进行容量分配更能增强系统的稳定性。对于孤岛微电网而言，安全稳定的运行，为系统内的用户提供高质量的电能是其工作的首要目标，因此综合各目标函数值，PSO算法较BSA算法的效果更优。

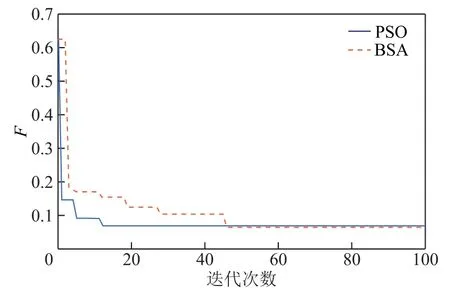
图6 PSO与BSA优化结果对比Fig.6 Comparison of PSO and BSA optimization results

图6为两种优化算法的迭代速度曲线，PSO算法的迭代次数约为 13次，BSA算法的迭代次数约为46次，这表明PSO算法的收敛速度更快，也验证了使用 PSO算法进行电氢微电网容量配置的有效性和优越性。

4.4 权重系数对容量优化配置结果影响

采用 PSO算法对微电网系统进行容量优化配置，保持其他条件不变，改变目标函数中的权重系数，分析权重系数对容量优化配置结果的影响。方案 1：w1=0.5、w2=0.3、w3=0.2；方案 2：w1=0.8、w2=0.1、w3=0.1；方案 3：w1=0.2、w2=0.4、w3=0.4。其优化结果见表5。

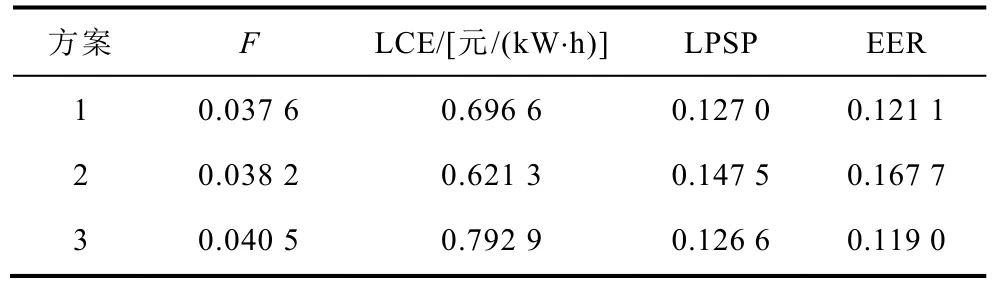
表5 不同权重系数下微电网系统优化结果Tab.5 Optimal configuration results of microgrid systems with different weight coefficients

当供电可靠性在目标函数中所占比重越小时，单位电量成本越低，系统可靠性越差。这是因为电解槽-储氢罐-燃料电池储能系统的单位功率成本高于光伏阵列和蓄电池的单位功率成本，经济性较电储能装置的小，同样系统在优化配置中倾向于剩余能量和牺牲系统可靠性，以此减少单位电量成本。因此会配置更大容量的光伏阵列和蓄电池，而配置较小容量的氢储能装置。因此在进行容量配置时，应合理评估经济性和可靠性的重要程度。

4.5 半实物验证

为验证本文配置结果及运行控制策略的有效性，使用RT-LAB半实物仿真平台进行测试。RT-LAB是由加拿大 Opal-RT Technologies推出的一套针对电力系统及电力电子实时仿真的运行平台，完全集成Matlab/Simulink，它可将基于Simulink搭建的数学模型通过上位机和目标机实现实时运行，并且可以通过上位机对运行过程进行监控。近年来广泛应用于国内外相关科研机构。

图7为RT-LAB实时仿真平台结构。仿真平台型号为OP5600HILBOX，运行速度为3.3GHz，本实验中运行步长设为0.1ms，仿真时间设为1天。各设备运行结果如图8所示。电储能及氢储能系统状态如图9所示。

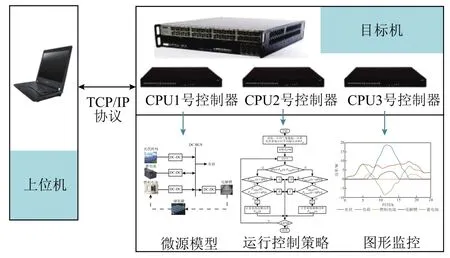
图7 RT-LAB实时仿真平台Fig.7 RT-LAB simulation platform

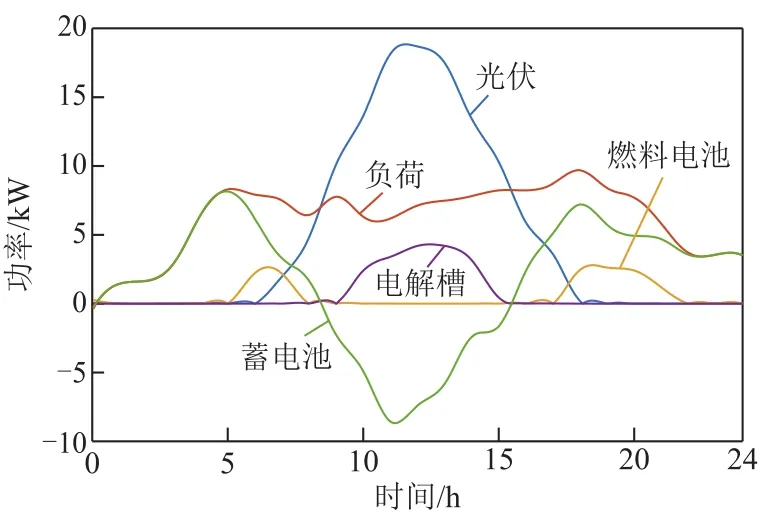
图8 系统功率曲线Fig.8 Power curve of system

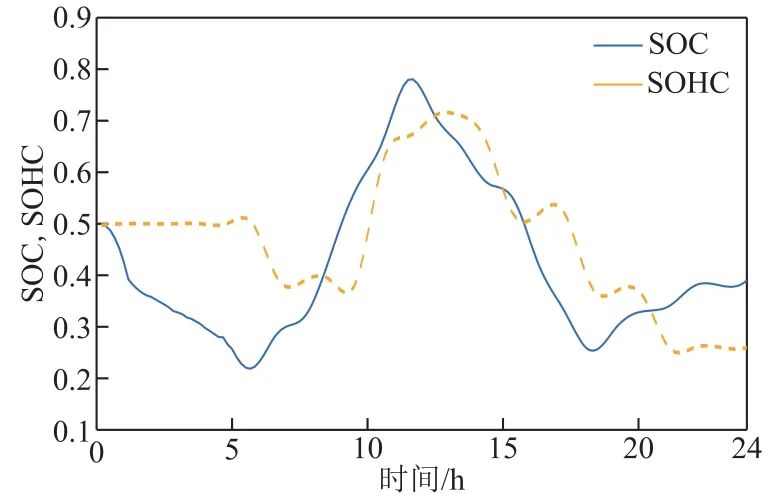
图9 系统储能状态Fig.9 State of energy storage system

由仿真实验结果可以看出，本文所提方法能够对系统内各设备进行有效的功率分配。当光伏输出功率小于负荷所需功率时，蓄电池优先放电，为负荷提供电能，若蓄电池所供能量不足以满足负荷缺额功率时，由燃料电池发电提供所需能量；当光伏输出功率大于负荷所需功率时，蓄电池优先充电储存能量，剩余弃光能量再供给电解槽进行制氢。电储能系统和氢储能系统存在互补特性，减少了弃光现象的发生，提高了能源利用效率，同时也提高了储能系统的储能稳定性。实验结果证明了本文所提微电网运行控制策略的有效性，该策略可以实现功率的缺额的高效补充及母线电压和功率流的平衡。