基于Surrogate优化建模方法的预装式氢储能电站结构布局优化
2021-02-22袁铁江
杨 南 袁铁江 张 昱 张 龙
(1. 大连理工大学电气工程学院 大连 116024 2. 国网新疆电力有限公司电力科学研究院 乌鲁木齐 830092)
0 引言
有一定移动能力的便携式电能供应设备是应对海岛、边防哨所等远离大电网的孤岛环境电能供应的最佳选择。当前,国内部分商业公司将储能元件、散热系统和控制系统安装在一个标准集装箱内,并将散热设备、电缆等辅助设备集成于箱体内壁中,开发出一种移动便捷、可快速部署的便携式储能系统。当前对此种储能集装箱的命名尚未有统一的说法,工业界一般称之为预制舱或预装式,本文因项目要求,统一称为预装式储能电站,此电站已经陆续在新疆等地的孤岛电网场景中得到了应用。利用预装式储能电站构建微电网,可以平抑孤岛电网中的新能源功率波动,维持“源-荷”平衡与微电网稳定运行,是解决孤岛电能供应的重要选择[1-4]。
预装式储能电站的散热设计本质上是集装箱散热设计。鉴于其内部元件集成度高,装置长时间高负荷运行的特点,主流的散热方式有风冷和液冷两种。液冷因为结构复杂,设计与控制过程复杂,不适用于箱体较大的集装箱散热。风冷又细分为自然通风和机械通风。前者利用百叶窗等无压力的设备实现自然通风,作为空气交换的进风口;后者利用风机等有压力设备将空气排出集装箱,实现箱体内外的气体与热交换。风冷系统结构简单,设计便捷,适用于箱体较大,发热量适中的箱体。文献[5-7]采用理论模型,研究了集装箱进舱后舱室内部的通风散热问题,探索了不同通风形式下舱室温度分布,利用变频风机对舱室内部通风进行改造的方法,送风量散热量对温度分布的影响等。文献[8]进一步指出,排风与送风模式下温差有较大差异,冷凝器在集装箱中的位置对排风模式影响较大,应采用送风模式散热效果最佳。文献[9]分析了35kV的STATCOM在直挂式集装箱的散热问题,采用的是通过分析开关器件运行方式获取STATCOM元件热特性,再将其代入散热系统中研究利用风机选型与集装箱结构变化解决功率单元散热器进口风速不一致的问题的方法。与之类似的有研究散热器与 IGBT温度分布的[10-11],静止无功发生器(Static Var Generator, SVG)设备功率柜的[12-13]。近年来,关注锂电池储能系统散热设计的文献日益增加,如文献[14]关注了锂电池 Pack的散热问题,采用计算流体动力学(Computational Fluid Dynamics, CFD)传热模拟方法对电池机柜进行了研究,指出改进电池间隙、集流板倾斜设计、风扇速率等方法可以有效改善电池散热性能。与之类似的还有文献[15-18],分别考虑电池本体、光伏电池板和逆变器变流器等电力电子元件的热特性,研究静态锂电池在集装箱设备中的散热情况。文献[19]在综合以上结论的基础上提出了一种双向连接低压电网的192kW·h盐酸铁锂电池柜的散热设计,并分析得出此设计的全周期工作效率大约在70%~80%左右。
通过上述分析可以看出,目前储能电站的研究主要集中于锂电池储能电站,其作用是对大电网波动提供短时的功率/能量支撑[20-22],与之对应的散热研究也多集中于锂电池及其配套电力电子设备相关的散热设计,结果具有很强的针对性,在电/热理论模型较为成熟的锂电池或其他电气元件散热有着很好的实践。但其设计方案的评估与优化依赖综合性工程仿真软件,如ICEPACK,不适用于较为复杂的多物理量元件,如燃料电池,缺乏普适性。
近年来,有学者提出作为一种长期能量型储能单元,氢储能的充电与放电是独立存在的,可以通过氢气的传输与转移克服储能元件“收放平衡”的需求,更加适应独立微电网持续稳定供电场景[23]。然而,氢储能元件的加入,必将改变预装式储能电站的热特性。为了在保证预装式氢储能电站供电可靠性的同时提升系统的能量供应,需要综合考量燃料电池的热特性与集装箱内部散热分布特点,探索在体积有限的预装式储能电站中,使储能单元散热效果最好的同时取得最大功率的布局模式。此问题的难度在于,前者涉及流体力学、热力学、电化学等多个学科在微观尺度上(mm级)的综合模拟,后者则是热力学与流体力学在宏观尺度(m级)上的设计优化。对于此种多物理量变尺度的联合仿真与设计,模拟尺度不一致,仿真软件结果不通用的问题会导致设计的优化无法协调进行,影响优化的精确性与完整性。
针对此问题,本文提出一种基于Surrogate建模优化算法的结构优化方法,通过对模拟结果的数据建模,将有限元计算的结果拟合为数值模型,使其可以应用传统的数学计算软件进行优化计算。在保留部分有限元结果精度的前提下,大幅度降低算力需求,为多物理量变尺度的工业设计优化问题提供了一种新思路。
1 质子交换膜燃料电池(PEMFC)仿真设计及优化
1.1 质子交换膜燃料电池的原理及其结构分析
质子交换膜燃料电池(Proton Exchange Membrance Fuel Cell, PEMFC)是氢储能电站的核心元件,为满足预装式氢储能电站在有限空间内提升功率的需求,PEMFC必须拥有较高的功率密度,即功率体积比。为探究 PEMFC的极限功率体积比,本节针对 PEMFC的结构设计进行了优化,求取在结构设计可行范围内功率的极限变化范围,用以规划氢储能电站散热布局方式。PEMFC的结构如图1所示,由流道、气体扩散层、电极和质子交换膜组成,其工作原理为:
(1)氢气经过阳极流道扩散到达阳极催化层,在催化剂作用下被氧化,生成氢离子与电子。
(2)电子通过电极被引入外电路,形成电流供给负载。
(3)氢离子透过质子交换膜到达阴极,与同样透过阴极扩散层的氧气发生反应,生成水并产生热量。
(4)阴极侧大部分水顺空气排出,少部分因压力差透过交换膜向阳极扩散。

图1 PEMFC全结构Fig.1 Full structure of PEMFC
整个反应的过程可表达为
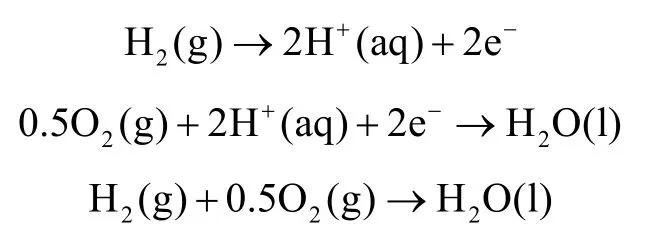
如果将单独的一条流道拆解来看,其结构如图2所示。
图2 单沟道PEMFC结构Fig.2 PEMFC structure in channel
为求解PEMFC的功率范围,依据PEMFC原理将 PEMFC功率计算的过程分解为二次电流分布计算、阳极扩散过程、阳极浓分子传输过程、阴极扩散过程和阴极浓分子传输过程五个部分。分别采用:考虑电化学反应中活化损耗的Nernst-Planck方程式(1),考虑多孔介质中浓物质扩散的Brinkman方程式(2),考虑反应物浓差极化与电化学活化极化影响,反应电流随电极电势变化关系的 Butler-Volmer方程式(3),及数个控制方程(质量守恒、动量守恒和通量方程)。

式中,um,i为迁移率;lϕ为电解质电位;U为速度矢量;Ni为化学物总通量;zi为物质i的带电量;Fci为常数。

式中,U为流体速度矢量;p为压强矢量;k为离散颗粒的形状修正系数;μ为液体运动粘滞系数。

式中,iloc,m为局部电荷转移电流密度;i0,m为交换电流密度;αa,m为阳极电荷传递系数;αc,m为阴极电荷传递系数;R为气体常数;T为温度;ηm为局部过电势;F为法拉第常数。
将某型PEMFC的典型参数输入COMSOL有限元软件,其氢氧分子浓度、沟道内电流密度分布,在 0.4V电压下,单沟道的电流密度,阴极/阳极气体分布,如图3~图6所示。

图3 沟道电流密度分布图Fig.3 Current density distribution in channel
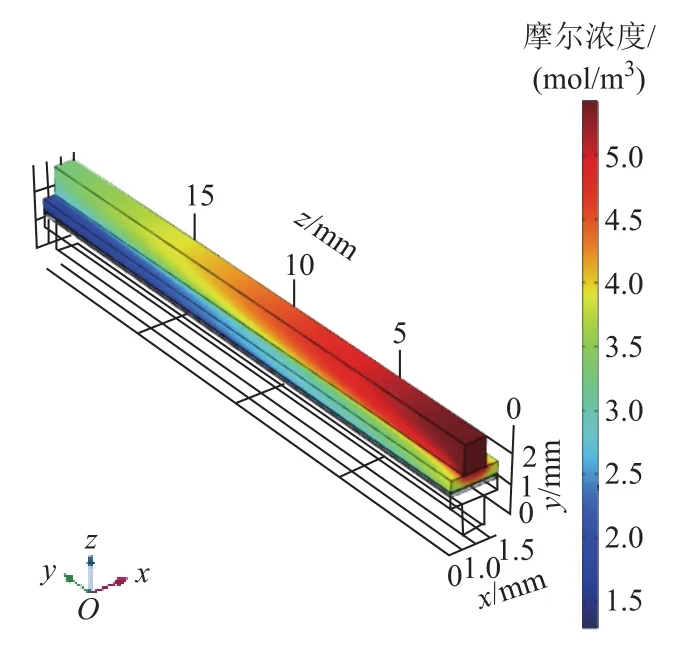
图4 阴极氧气摩尔浓度图Fig.4 Oxygen concentration in cathode

图5 阳极氢气摩尔浓度图Fig.5 Hydrogen concentration in anode

图6 燃料电池水分子含量图Fig.6 Water concentration in fuel cell
由图3~图6可知,随着沟道长度的延伸,氢氧分子逐步反应,浓度下降,水分子浓度上升。沟道末端氢氧分子几乎耗尽,反应较为完全,对应的电流密度也逐步下降。电流密度分布随氢氧浓度的下降而逐步下降,在沟道内的电流密度分布各不相同。
对于预装式氢供能电站,需要在狭小的空间内安排尽可能多的燃料电池,因此,燃料电池的体积功率比是十分重要的。由于电子纵向穿越气体扩散层(Cas Diffusion Layer, GDL),电极与质子交换膜,三者的厚度直接决定电阻,是导致电流密度变化的原因之一。而质子交换膜的厚度受限于工艺,大致在1mm左右。因此其余两者被选择成为变量。而电极、气体扩散层和质子交换膜三者共同的宽度亦是决定电流密度分布的重要因素。综上所述,本文选取三个非流道参数(气体扩散层高度Hgdl,电极高度Helectrode,电极、气体扩散层、质子交换膜三者共同的宽度Wrib)作为设计变量。通过此三变量的设计,希望找出 PEMFC在现有设计条件下极限功率密度的取值范围,为预装式氢供能电站的散热设计提供基础。
1.2 基于Surrogate建模方法的PEMFC结构优化
当前 PEMFC设计领域常用的优化方法有:基于解析式的数学优化与基于有限元的数值优化。由于设计时间与算力的需求,前者往往采取较为简单的物理公式,导致仿真精度不高。而后者虽然仿真精度较高但仿真时间极长。如果采取有限元仿真+智能搜索算法结合的方法设计,以一次迭代有限元计算半小时为标准,结合常见的粒子群算法(Particle Swarm Optimization, PSO)或遗传算法(Genetic Algorithm, GA)搜索平均需要的200~500次迭代,其设计时长是相当惊人的数百小时。精度与速度的矛盾是结构设计优化领域的一大问题。
本文采取一种基于数据驱动的 Surrogate建模方法(可翻译为伴随建模或替代建模)来处理此问题。代理模型技术是利用有限的已知数据构建预测模型,从而近似拟合方法,可以大幅度地提高优化的效率,降低工程系统的复杂程度。本文通过有限的流体动力学模型测试数据构建代理模型,代替了复杂的有限元流体动力学模型,在基本保留有限元模型精确度的同时使得优化过程得以简化。本文构建的优化模型可以使用传统的数学优化软件进行,摆脱了联合仿真的需求,是多物理量复杂系统优化设计的良好技术方案。Surrogate建模的基本流程如图7所示。
首先,定义优化问题的变量、目标以及限制条件。对PEMFC优化来说,优化问题的变量为Hgdl、Helectrode与Wrib,目标为功率密度最大,限制条件为


图7 Surrogate建模优化流程Fig.7 Flow chart for surrogate optimization
由此可知,变量空间为一个三维空间。为构建一个足以精确描述功率与变量关系的目标函数,基本思路为在此三维空间内采样,通过样本不断修正预测模型参数与样本实际值之间的差距。因此,采样点的选取原则应为:在变量空间内部以尽可能少的采样点获取尽可能多的信息,即采样点应在样本空间内均匀分布。为达成此目标,本文采取拉丁超均方抽样方法设计抽样方案,即图7流程中的设计实验环节,其具体过程为:将变量空间分割为数个分段,每个分段在抽样中被抽中的概率是独立且随机的,但每个分段中有且仅有一个点能够被选中。对此方法的数学解释为
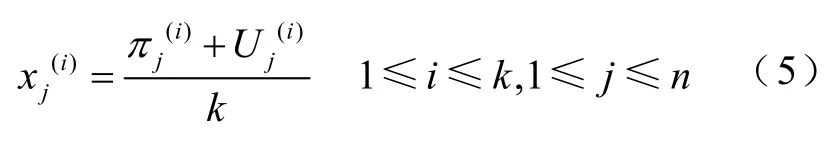
式中,U为一个在[0,1]区间内的随机值;π为一个在0到k-1范围内独立随机的排列;下标j是变量维数,下标i是当前样本序号,k为样本数量;n为变量维度;x为样本点。
此后,通过 COMSOL有限元模拟软件对样本点的目标函数进行测试,并建立预测模型。Surrogate建模的预测模型大致有两类:含参模型与不含参模型,前者如多项式模型、神经网络模型;后者如径向核函数模型、科雷金模型。前者的基本形态是固定的,如多项式模型:即预测值ŷ有常数项β0与一组线性多项式(权重系数β0与变量xi)之和构成。

求解此类模型的关键在于寻找合适的参数使模型预测误差最低,非常适用于计算机寻优,缺点是预测非线性度不足。
克里金模型是地质学上常用的一种基于插值方法的预测模型,其核心思想为:未知点的取值可由已知点与预测点的距离,已知点整体空间分布排列计算而成,即


在上述公式的计算过程中,需要使用协方差矩阵与描述预测值和实际值偏差随距离变化的半变异函数,本文采取高斯随机过程对这一函数进行描述,即

式中,R为一个p阶的协方差矩阵,其中每个元素Rj1,j2=R(xj1,xj2),即样本点xj1与xj2之间的关联性方程,这里采用高斯关联性方程,即式(10);σ为方差;θk为参数。
由此,可将求解式(8)的过程简化为求解式(11),求解使式(11)达到最大值的一组θj,即可得到一个能准确预测目标与变量关系的Surrogate模型。

科雷金法由于采取非线性的预测公式,对现实问题具有较好的模拟特性,本文采用样本点与科雷金法建立Surrogate模型以替代有限元模型,并通过Matlab等数学计算软件的智能算法(本文采取 PSO算法)工具箱进行计算,从而规避了商业有限元软件计算结果不通用、优化调用较为复杂的困难。针对PEMFC的优化,本文选取样本数据总量N为30组,通过选取样本数据总量的80%,即24组样本量进行样本训练,6组样本数据进行对照。结果见表1。

表1 PEMFC优化及测试结果Tab.1 Optimization results of PEMFC and its validation
由表1可知,PEMFC在此结构设计中,最大功率密度为0.4W/cm2,最小功率密度为0.27W/cm2。由图8可知,不同电压下电流密度的大小非线性变动,最大功率点随PEMFC几何参数的变化而变化,规律较为复杂。优化后无论是功率曲线还是电流曲线相对原始设计均有一定程度的提升。
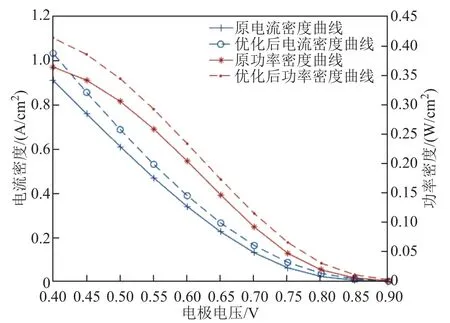
图8 电压-电流/功率密度分布Fig.8 Voltage-current/power density distribution
GDL厚度对功率密度的影响较大,最优与最劣方案分别取在了上、下限。Wrib对功率密度的影响适中,最优值出现在中间,而电极厚度Helectrode最优最劣方案几乎没有变化,猜测此数值与 PEMFC的功率密度没有直接关系。参考文献[24-25],本文采取了 Sobol敏感性指标对上述变量对结果的影响进行了分析,如图9所示。
Sobol方法是基于方差分配的全局敏感性分析方法,该方法认为模型函数可分解为单个变量的函数之和,则单个变量的方差可由近似蒙特卡洛数值积分进行核算,此时模型的总方差D可以表达为
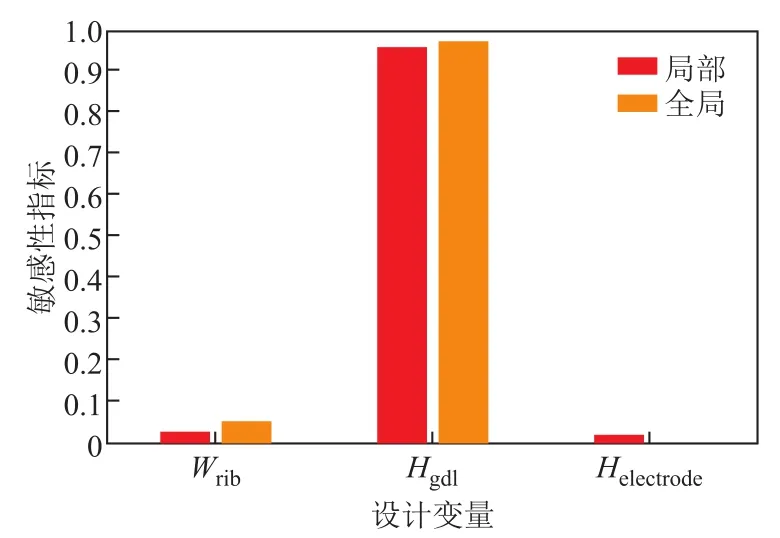
图9 PEMFC功率优化敏感性分析Fig.9 Sensitivity analysis for power optimization in PEMFC

式中,Di为变量Xi通过变量Xi作用所贡献的方差;Di,j为变量Xi通过变量Xi、Xj所贡献的方差;Di,j,…,n为变量Xi通过变量Xi,j,…,n所贡献的方差。
定义变量与变量间相互作用的方差与总方差的比值为敏感性指标Si,其反映了变量Xi与模型输出总方差的直接贡献率,即

同理,二阶敏感性系数为

变量Xi的总敏感性指标为各阶敏感性指标之和,即

结果证明,GDL厚度对功率密度的影响是沟道宽度的10倍以上,而电极厚度仅仅在局部对功率密度有影响,如果考虑蒙特卡洛抽样误差的情况下可以认为其几乎没有影响。
在考虑优化时间的前提下,本次优化采用PSO优化工具,优化了118代,每代30个个体。如果采用传统有限元模拟法,以单次有限元模拟30min计算,需1 170h。采取Surrogate优化算法,采取了30组样本,样本测试时间为 15h,优化计算时间约为0.5h,总耗时15.5h。极大地提升了计算时间的同时,最终结果与有限元设计误差在 5%之内,可以验证Surrogate算法在精度与速度上的优越性。
由优化结果可知,PEMFC的功率密度大约在4kW/m2至 2.6kW/m2,考虑到生产厂家的差异,PEMFC的效率在60%~80%不等,取中间值70%计算,PEMFC热密度大约在780~1 200W/m2。
2 预装式氢储能电站散热设计
2.1 散热方案选择
如前所述,本文探索的是预装式氢储能电站在有限的空间内能够达到最大功率值。因此,散热方案的选择对预装式氢储能电站的设计是至关重要的。
液冷和风冷是散热设计的两种常规方案。液冷系统方案需在发热体外侧构建封闭式的散热管道,使用额外的液压泵驱动冷却液流经发热体带走热量。此方案结构复杂,控制困难,且有一定的冷却液泄漏风险,适用于箱体小,发热量较大的场景。对于箱体较大、发热量适中的预装式氢储能电站,直接通风式风冷散热系统结构因其结构简单、设计方便和散热效果适中的特点更适用于预装式氢储能电站。
传统冷藏集装箱的风冷设计,其冷负荷主要来源于:①外部空气与车体外壁面的强制对流换热;②车体内外壁的温差;③太阳辐射;④车体内壁与空气的换热;⑤密闭性不足导致的漏热。对于此类集装箱常见的瓜果运输来说,货物本身的散热量较小。此类集装箱式的常规散热方法是空调从上部供应冷空气,自下部自然对流排出热空气,即进出风口垂直同侧。考虑到对于氢供能集装箱而言,氢气浓度是安全性的重要考核指标。而氢气较轻,泄漏氢气会向上扩散。将回风口放在箱体上端,可以有效地排除泄露氢气。因此,出风口的位置是氢储能电站散热设计的重点。
本文在考虑出风口位置时,主要考虑了三种方案:同侧下出风,邻侧下出风,双侧下出风,并对三种情况下箱体温度、风速进行了模拟,结果如图10~图15所示。

图10 方案一温度/气流分布图Fig.10 Temperature/streamline distribution for Plan 1

图11 方案二温度/气流分布图Fig.11 Temperature/streamline distribution for Plan 2

图12 方案三温度/气流分布图Fig.12 Temperature/streamline distribution for Plan 3

图13 方案一风速分布图Fig.13 Wind speed distribution for Plan 1
由图10可知,方案一电池架最高温度399K,最低温度304K,温差95K,箱体后部温度明显高于前部。远风口电池架最高温 399K相对近风口高出35K左右。对比图13的风速可知,此方案风速与温度成正比,由于回风口与进风口距离过近,远端风速几乎为 0,冷却风难以触及,只能靠自然换热降温,从而导致末端温度过高。

图14 方案二风速分布图Fig.14 Wind speed distribution for Plan 2

图15 方案三风速分布图Fig.15 Wind speed distribution for Plan 3
同理,方案二相对于方案一效果更好。全电池架最高温387K,最低温324K,温差63K,相对方案一均有所下降。但箱体前后部电池架温度不一致的问题依旧存在。最高温出现在箱体远风口下部风速几乎为0的部分,原因与方案一类似。
方案三是三种方案中最好的。全电池架最高温度335K,最低温度290K,温差45K,均高于另两种方案。风速分布也较为均匀。因此,本文选择此双向进风,顶部回风的方案作为通风方案。
2.2 基于Surrogate的散热方案优化设计
如前所述,本文的目的是探索预装式氢储能系统在双进风方案下能达到的极限功率,即在保证温度在一定范围内的情况下,如何安排通风道,使PEMFC的功率最大化。
为提升散热模拟的可靠性,在此方案基础上做出两个改进:①将发热面的设置改为四层结构,不再使用地面作为发热面;②将进风口设置为矩形,符合传统空调出风口的形状,但出风口因为有排出氢气的作用,采取风扇排风,圆形出风口不做更改。
某公司制造的预装式氢储能系统散热方案为空调侧进风,风扇顶回风,符合案例中方案二的设计思路。故本文将其改进为双侧空调进风,顶端风扇排风的方式。改进型预装式氢储能系统基于一个标准的 20英尺集装箱(5400mm×2200mm ×2200mm),其结构如图 16和图 17所示。根据 2.1节末的叙述,将设计变量定义为:进风口宽度WAC,进风口高度HAC,进风口下端距地面距离HCAC,排风道宽度Vw,PEMFC的功率密度Ppu,如图 18和图 19所示。前三者决定了进风口的大小、位置,后两个参数则确定了箱体内可以安装的最大功率值。此五个参数共同决定了箱体温度的分布。理论上,高功率密度越高,其需要的散热通道也就越大,因此将箱体内最高温度设为约束条件,将箱体总功率P设为目标,并根据箱体尺寸约束变量取值范围,优化可写为

图16 预装式氢储能电站外部结构Fig.16 Outer structure for pre-manufactured hydrogen energy storage power station
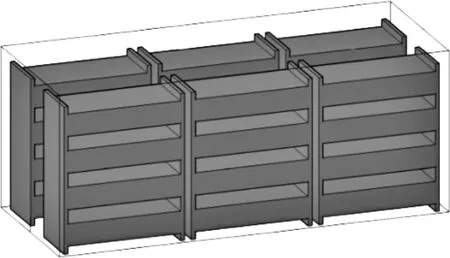
图17 预装式氢储能电站内部结构Fig.17 Inner structure for pre-manufactured hydrogen energy storage power station

图18 预装式储能电站左视图Fig.18 Left view of pre-manufactured hydrogen energy storage power station
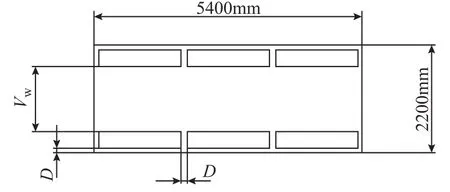
图19 预装式储能电站内部俯视图Fig.19 Top view of pre-manufactured hydrogen energy storage power station

在此优化中,温度与变量之间的关系由Krigging方法建模得出,为隐函数,无法以代数形式进行表达。P的公式虽然可以用简单代数方程式(16)表示,但此处依旧采取Krigging建模的方法,并在最后的敏感性分析中对建模的准确性加以验证。

式中,D为电池架与墙壁/电池架的间隔;η为PEMFC的效率。
基于Kriging建模方法的Surrogate优化一般取样本量的80%训练,取样本量的20%进行数据检测。一般认为平均相对误差在±10%以下即可接受。针对样本数据的检测结果,已知目标函数的实际测试值为Pi与Ti,基于代理模型的数据拟合结果为Pipredict与Tipredict。则构建误差检测模型为式(17)所示,整个优化的流程如图20所示。


图20 优化流程Fig.20 Flow chart for heat dissipation design
3 算例分析
3.1 样本数据测试
以某公司的预装式微网锂电池储能电站采取的20英尺(标准集装箱)箱体为例,该储能电站箱体外壁长5 600m,宽2 400m,高2 600m,所用储能电池功率50kW,50kW/h,取内壁长5 400m、宽2 200m、高2 200m计算。在第2节所述的范围内,使用拉丁超均方抽样法抽取50组样本数据进行测试,选取样本数据总量的80%,即40组样本量进行样本训练。利用剩余10组样本数据进行误差检验。测试结果见表 2。测试结果表明,平均相对误差均小于 10%,可以通过误差检测。

表2 样本数据测试结果Tab.2 Test results for sampling data
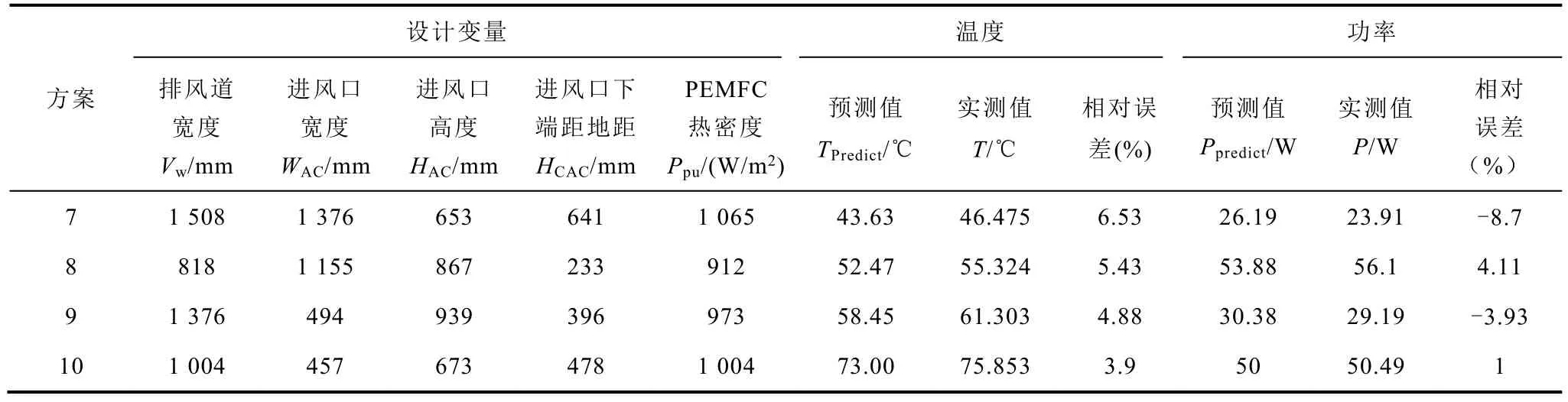
(续)
3.2 最优方案解析
根据本文所建立的基于Surrogate算法的优化模型及Ansys CFX的测试结果,通过粒子群算法求解,可以得到最优的预装式储能电站的布局方案见表 3。

表3 预装式储能电站最优预测方案Tab.3 Predicted optimization plan for pre-manufactured hydrogen energy storage power station
为验证上述优化结果,对最优布局的预装式储能电站设计方案采取 Ansys CFX有限元软件进行热分析计算。预装式储能电站最优方案预装式储能电站的网格划分如图 21所示。设置进出口风速为3m/s,风温为 10℃,箱体内气压为 1atm(注:1atm=101.325kPa),出口气压为1atm(即自然出风,不加压),设置电池架的四个发热面底部为发热面,设置收敛精度为1×10-4。温度场收敛后电池架温度分布图、出口温度分布图和内部截面风速如图22~图25所示。

图21 预装式储能电站网格划分图Fig.21 Grid mesh of pre-manufactured hydrogen energy storage power station

图22 电池架温度分布3D图Fig.22 Temperature distribution of battery racks in 3D

图23 出口温度分布图Fig.23 Temperature distribution of outlet

图24 集装箱内部截面风速图Fig.24 Wind speed distribution inside container

图25 电池架温度分布2D图Fig.25 Temperature distribution of battery racks in 2D

表4 预装式储能电站最优方案Tab.4 Validated optimization plan for pre-manufactured hydrogen energy storage power Station
预装式储能电站最优方案见表4。由表4可以看到,最优的布局方案为散热通道宽度为500mm,进风口宽度为1 770mm,进风口高度为951mm,进风口下端距地距为200mm,PEMFC热密度为1 200W/m2,此时预装式储能电站的预测容量为 89.93kW,此时的温度估计值为57.5℃,实测容量为90.75kW,实测温度为57.11℃,误差均在1%以下。参考原集装箱锂电池50kW/55℃的标准,以温度上升3.8%的代价,提升了81.5%的功率。
通过分析此数据可知,即使将通风道的宽度优化在工作人员侧身可以进入的500mm的下限,依旧可以通过改善通风口的大小、位置等变量,以10℃的冷却风将PEMFC的工作温度控制在60℃以下。由图25可知,在此种分布下,冷空气的入口布置在较低的位置。进风过程中冷空气接触到位置最低的发热源,被逐步加热上升。最后由顶部的出风口被抽出,冷空气在箱体中的分布较为均匀。但中央底部因为冷空气覆盖不到产生了一个局部热点。在实际生产过程中应对此处的 PEMFC予以额外的冷却措施,进一步降低箱体内温差。
对比图24与图25可知,风速覆盖的部分温度较低。箱体温度分布较为均匀,没有明显的纵向温差。被风速较好覆盖的前部与后部电池架,最高温度320K,最低温度315K,温差仅为5K。中央电池架的底部由于冷空气速度较低,最高温度达到了329K,最低温度为315K,温差14K。但仍然可以保证PEMFC温度在60℃以下。
针对目标与变量之间的关系,沿用第1节末的方法进行了敏感度分析。功率与变量之间的敏感性关系如图26所示,温度与变量之间的敏感性关系如图27所示。根据敏感性分析结果验证,功率仅与通风道宽度Vw和PEMFC热密度Ppu有直接关系,符合解析式(12)的描述。在所有五个变量中,通风口的高度对于温度和功率的影响都不算大,因此维持其在一个相对正常的数值即可。对温度影响较大的除了Vw之外,HCAC和WCA的影响也不可忽略,这是因为风口位置直接决定了风在箱体中的运动轨迹,而风口的宽度直接决定了进风量的大小。这两者的共同作用影响了冷却风能够接触到的 PEMFC表面积。风口越低,冷却风在箱体的垂直运行轨迹就越长,所能起到的换热作用就越明显。而进风口的宽度决定了冷却风水平运动的轨迹,宽度越大,单位高度内能够接触的 PEMFC表面积也就越大。数据敏感性分析的结果表明:在实际生产中,进风口应设计成较为扁平的矩形,设置于箱体前后两侧的中下部较为合适。

图26 散热优化敏感性分析(功率)Fig.26 Sensitivity analysis for heat design(power)

图27 散热优化敏感性分析(温度)Fig.27 Sensitivity analysis for heat design(temperature)
4 结论
1)本文探讨了预装式氢储能电站主要热源PEMFC的功率密度问题,通过对PEMFC的结构设计优化,可以将氢储能电站的功率密度提升至4kW/m2,相对于原系统采用的锂电池5kW/m2的功率密度相差不大。
2)在考虑PEMFC功率密度及工作效率的前提下,本文针对预装式储能电站的通风散热问题,分别测试了回风口在上,进风口在三种方案下储能电池架的温度。结果表明,进风口双侧进风对流的散热效果最好,温度分布最均匀。进而选择Surrogate方法对预装式储能电站的具体散热设置进行了优化测试,有限元测试结果显示:通过采取扁平矩形的低位进风口,可以在原设计的基础上,以温度上升3.8%的代价,提升原设计81.5%的功率。
3)针对传统有限元搜索优化算法运算时间长,算力需求高的问题,本文通过Surrogate优化算法对有限元模型进行了简化,将原本数百小时的优化过程缩短至 1~2h,同时将误差成功控制在 10%以下。通过数值模型的构建,此方法克服了现有研究有限元软件与优化计算软件不通用的问题,为此类多物理量变尺度的工业设计问题提供了有效的参考方案。
