计及功率密度约束含氢储能的预装式多元储能电站容量优化配置研究

袁铁江 张 昱 栗 磊 曹新慧 杨 南

（1. 大连理工大学电气工程学院 大连 116024 2. 国网宁夏电力有限公司电力科学研究院 银川 750002 3. 国网新疆电力有限公司经济技术研究院 乌鲁木齐 830011）

0 引言

海岛、边防哨所等偏远地区距离大电网较远、可持续供电难以保障，多采用包含储能系统的风力/光伏发电等分布式新能源微电网对其供电[1]。许继集团等公司将多种储能元件、散热系统、控制系统集成，开发出可移动、可快速部署的小型预装式微电网储能电站，为平抑新能源功率波动[2-4]，维持“源-荷”平衡与微电网稳定运行提供了新的手段。为实现该类储能集成系统效益最大化，储能单元的选择与储能容量的配置中，考虑集装箱体积形成的功率密度约束就显得至关重要。

目前，国内外针对微电网储能单元的选型及其容量优化配置方面做了大量的研究。文献[5]采用区间数和层次分析法相结合的方法，求解储能选型的问题。文献[6]用模糊理论和层次分析法开展简单对比选型，用以提高电能质量。文献[7]根据现有的天气和资源条件对系统容量进行了优化设计，但储能形式单一，无法满足各种工况下系统对不同种类储能的需求。文献[8-11]通过对风-光-储系统的数学机理建模和经济性评估，重点探究了独立新能源微电网的容量优化配置问题，并给出了解决方案，但在约束条件中未考虑储能单元剩余电量约束，可能造成求解结果不准确。文献[12]对风电场输出功率偏差进行频谱分析，最终确定储能系统容量和储能补偿后的系统备用需求。文献[13]利用单一蓄电池将城市轨道交通平峰期或低峰期回收的制动能量部分转移至高峰期，可以降低牵引变电所的建设成本，但蓄电池储能手段单一，并未考虑不同应用场景下对不同储能手段的需求，造成配置结果的片面性。文献[14]利用遗传算法对建立的蓄电池-超级电容器混合储能系统的容量优化模型及其约束条件进行求解；然而在涉及混合储能单元时，没有频谱分析的系统容量配置，可能会造成配置结果技术性、经济性不足。文献[15]研究了不平衡功率离散型傅里叶变换分断点的分断原则，建立孤岛型微电网混合储能优化配置模型，对储能容量优化配置进行分解，降低了模型的求解复杂性。文献[16]提出一种基于离散型傅里叶变换的主动配电网混合储能容量优化配置模型，并考虑市场环境中的分时电价和电能交易，优化混合储能系统充放电功率，减少了能量型储能系统的寿命损耗；但蓄电池的能量密度在当前市场上并非最高，所配混合储能系统的长时段供电能力不足。

目前市场上储能电站的配置大多选择超级电容器和锂电池的混合储能单元进行短时的能量支撑[17-23]。氢储能相比于锂电池可以长时间大规模储存能量，更能适应独立微电网极端持续稳定供电场景[24-25]，作为氢储能组成部分的燃料电池具有很高的功率密度[26]。氢储能的加入使得体积有限的预装式储能电站具有更高的功率密度与能量密度。超级电容器、锂电池和氢储能相结合的储能系统性能完备，可以满足不同场合的用电需求，使得预装式储能电站能够更好地适应海岛、边防哨所存在的长时间、大功率的用电需求。寻求计及功率密度约束的含氢储能的预装式多元储能电站容量优化配置方法对该类电站的应用是至关重要的。

因此，本文提出计及氢储能的预装式多元储能电站容量优化配置方法，依据微电网平衡功率的频率特性与多元储能单元补偿特性，划分补偿频段，计算缺电惩罚费用及能量溢出惩罚费用，再以年均投资成本最小为目标追求，以剩余电量、负荷缺电率及能量溢出率等为约束，采用遗传算法求解模型，得到储能电站的最佳容量配置方案。

1 基于频谱分析的微网功率分配策略

为分析微网功率分配策略，引入平衡功率的概念，对微网的平衡功率进行离散型傅里叶变换，将时序曲线转换为幅频特性下一系列的频率及其对应的幅值。根据频谱分析的结果与氢储能、锂电池和超级电容器的储能特性，划分多元储能单元的频率补偿频段。然后，将多元储能单元的补偿结果通过傅里叶反变换转换到时域，详细过程如图1所示。

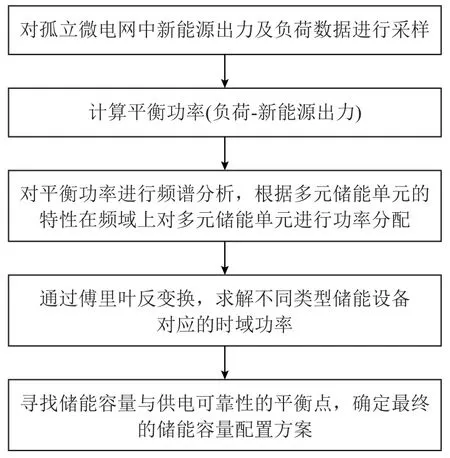
图1 多元储能单元功率分配策略Fig.1 Power allocation strategy of multi-component energy storage unit

1.1 功率平衡

根据微电网的实际风电、光伏发电和负荷数据，计算其实际平衡功率，对平衡功率进行离散傅里叶变换，得到一系列频率及其对应的幅值。根据多元储能单元的特性，确定多元储能单元的补偿，实现多元储能单元之间的功率分配。定义t时刻新能源系统的输出功率PRE(t)，所述的新能源系统包括光伏发电系统和风力发电系统。

式中，PPPG(t)为t时刻光伏发电系统的输出功率；PWIND(t)为t时刻风力发电系统的输出功率。

定义t时刻负荷功率PL(t)与新能源系统的输出功率PRE(t)之差为微电网的平衡功率PPH(t)，即

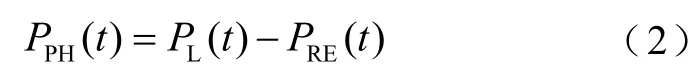
1.2 频谱分析及功率分配

根据微网中的光伏发电、风电出力及某一典型日负荷的采样数据，可以通过式（1）、式（2）得到微网中的时域平衡功率，如图2所示。

图2 某孤立微电网中的时域平衡功率Fig.2 Time-domain balancing power in an island microgrid

首先采集平衡功率样本数据。由奈奎斯特定理可知，采样频率大于采样信号中的最高频率的2倍时，采样之后的数字信号才可以完整地保留原始信号中的信息。采样周期越小，采样点越多，频谱分析的范围就越准确，本文采用的采样周期为 36s，即每小时采样 100个点，1 200倍频频率为1/(2×36)Hz，故基准频率为 1/(2×36×1200)Hz。

对样本数据PPH={PPH(1), ⋅⋅,PPH(n), ⋅⋅,PPH(N)}进行离散型傅里叶变换，得到经傅里叶变换后不同频率对应的幅值[27]为

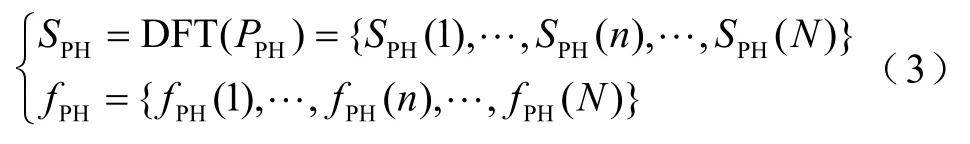
式中，DFT(PPH)为对微网的平衡功率样本数据PPH进行离散型傅里叶变换；SPH(n)为傅里叶变换之后第n个频率fPH(n)所对应的幅值；N为样本总数。

平衡功率的频谱分析结果如图3所示。平衡功率主要集中在低频附近，中、高频段幅值较小且呈现无规律波动。超级电容器功率密度大，充放电周期短，适合补偿短时高频波动，可作为功率型储能单元[28]；锂电池与超级电容器相比，能量密度大，持续供电能力强，可作为短期能量型储能单元；氢储能相比于锂电池具有更好的能量密度和更强的持续供电能力，可作为长期能量型储能单元。利用不同设备的响应特性合理分配多元储能单元之间的功率分配，保障系统供电可靠性。本文选择400倍频、800倍频作为分界点，将频谱分为三段，[0,400]倍频作为低频段，用氢储能进行补偿；[400,800]倍频作为中频段，用锂电池进行补偿；[800,1200]倍频作为高频段，用超级电容器进行补偿。为了更为直观地看清频谱分析结果，特挑选出前20倍频分析结果供读者观看。

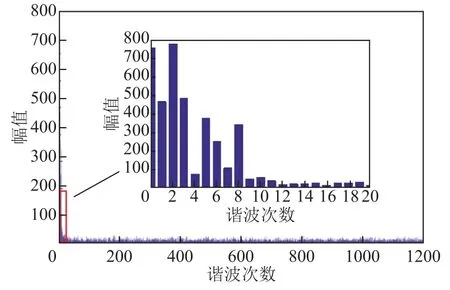
图3 平衡功率频谱分析结果Fig.3 Spectral distribution of balance power

根据上述补偿频段的划分，利用傅里叶反变换将氢储能、锂电池和超级电容器补偿频段的幅频结果转换到时域上，即可得到储能功率补偿结果。

假设fJL∪fJL1为锂电池补偿频段，其中fJL1表示SPH中以 Nyquist频率(频谱分析结果的最高分辨频率，为采样频率的1/2)为对称轴的与fJL对称的频段，其中fJL=[fJLmin,fJLmax]，fJLmin、fJmax分别为；电池补偿频段fJL的端点。用SL={SLi(nL),⋅⋅,SLi(NL)}表示频谱分析结果中锂电池储能单元补偿频段所对应的幅值，为了简化计算，将未补偿频段对应的幅值置为0，补偿频段的幅值不变，即

对锂电池储能单元补偿频段的幅值SL进行傅里叶反变换，将频谱分析的结果转换到时域，可以得到锂电池储能单元的补偿功率为

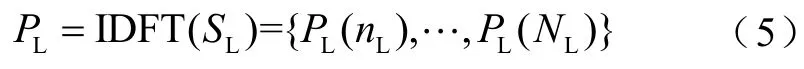
式中，nL表示的是频域划分之后的第nL个频率。同理可以得到超级电容器和氢储能的功率补偿结果。

1.3 补偿功率调整

在配置氢储能、锂电池和超级电容器的储能容量时，不能为了保证某些尖端负荷的正常用电而无限大地配置储能的容量。所以在配置储能容量时既要保证负荷用电的可靠性也要兼顾容量配置的经济性，即寻找储能容量与供电可靠性之间的平衡点。

以锂电池储能单元为例：当需要锂电池储能单元补偿的中频分量Pzp(t)＞0时，表示需要锂电池储能单元放电，假设配置的锂电池储能单元的功率为PLi0，则定义锂电池储能单元补偿的负荷缺电量为

则在整个寿命周期内，锂电池储能单元所补偿的负荷缺电总量为

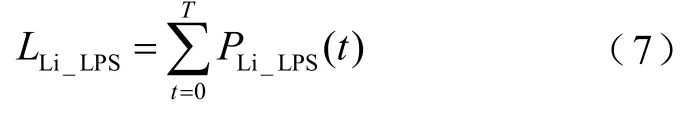
同理可以得到超级电容器和氢储能的负荷缺电总量分别为LC_LPS和LC_HPS，则定义负荷缺电率为

当Pzp(t)＜0时，表示需要锂电池储能单元充电，假设配置的锂电池储能单元的容量为PLi0，定义能量溢出量为

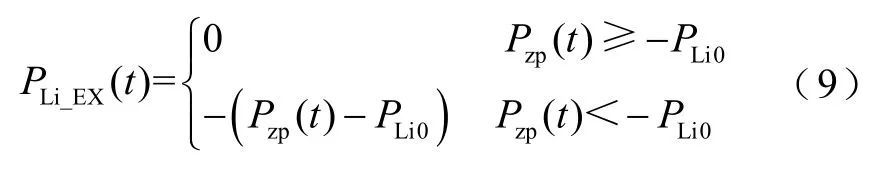
则在整个寿命周期内，锂电池储能单元所补偿的负荷能量溢出量为

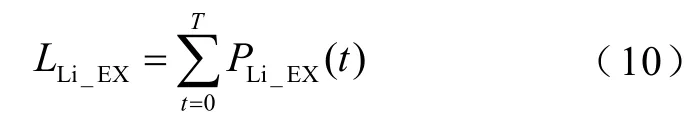
同理可以得到超级电容器和氢储能的能量溢出量分别为LC_EX、LH_EX，则定义能量溢出率为

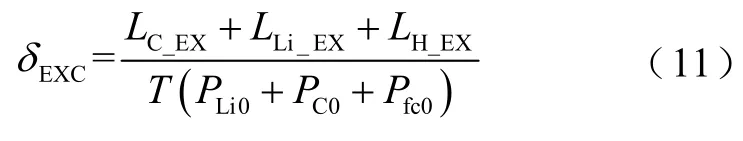
式中，PLi0、PC0、Pfc0分别为配置的锂电池、超级电容器和燃料电池的容量；T为研究周期。

2 多元储能容量优化模型

2.1 目标函数

根据新能源系统输出功率和负荷消耗功率的需求，合理配置氢储能、锂电池和超级电容器的容量，确定微电网系统年均综合成本最小为微电网储能容量优化配置的目标，建立微电网储能容量优化配置的目标函数为

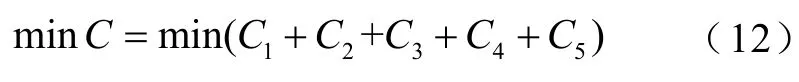
式中，C1和C2分别为氢储能、锂电池和超级电容器等设备的一次投资成本和运行维护成本；C3为缺电惩罚费用；C4为能量溢出惩罚费用；C5为体积成本费用。

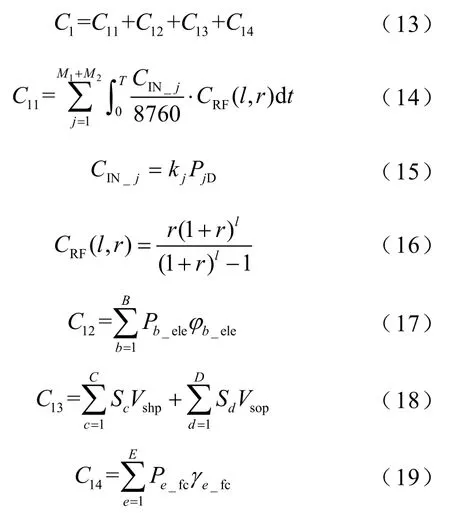
式中，C11、C12、C13、C14分别为超级电容器、电解槽、储气罐、燃料电池的一次投资成本；M1、M2、B、C、D、E分别为超级电容器、锂电池、电解槽、氢气罐、氧气罐和燃料电池的总数量；CIN_j为各个储能单元的初始投资成本，储能单元的初始投资成本与其额定功率的配置有关；kj为各个储能单元的功率系数；PjD为各个储能单元的额定功率；CRF为资金回收系数；r为利率；l为超级电容器和锂电池的使用年限；Pb_ele为单台电解槽j的功率；φb_ele为电解槽单位功率价格；Sc、Sd为体积单价；Vshp、Vsop分别为氢气罐和氧气罐的体积；Pe_Fc为单台燃料电池的功率；γe_fc为燃料电池单位功率价格。

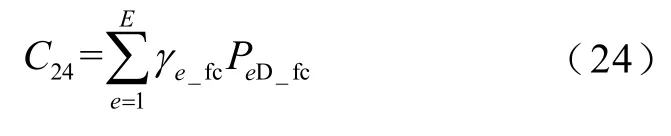
式中，C21、C22、C23、C24分别为锂电池和超级电容器、电解槽、储气罐、燃料电池的运行维护费用；jγ为运行维护成本系数；EjD为各个储能单元的额定容量；CRe、CRs为电解槽和储气罐的年维护费用系数；Mbt为第b台电解槽在第t年的运行费用；εjt为第j瓶储气罐在第t年的运行费用；γe_fc为燃料电池的单位容量维护系数；PeD_fc为燃料电池的额定功率。

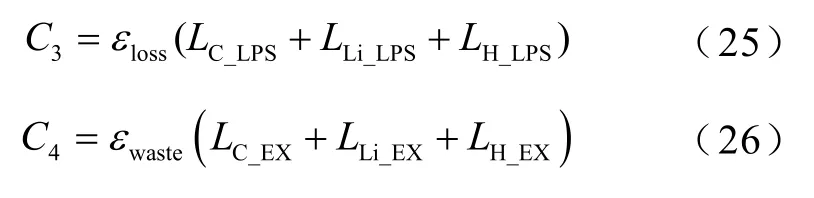
式中，εloss为负荷缺电惩罚系数；εwaste为能量溢出惩罚系数。

集装箱的制造需要一定的成本，故引入体积成本费用C5。

式中，εtotal为体积成本系数。

2.2 约束条件

2.2.1 储能单元剩余电量约束

考虑到储能单元的寿命，其剩余电量都应该控制在合理的范围内。因此，t时刻超级电容器、锂电池和氢储能剩余电量约束可以表示为

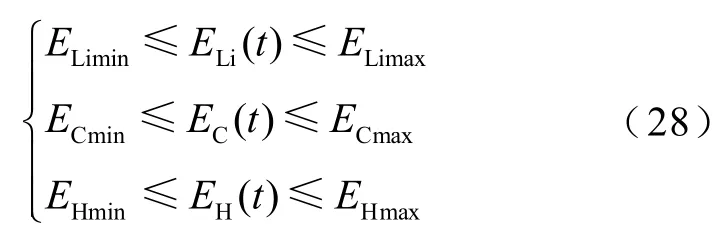
式中，ELimin、ELimax分别为锂电池储能系统的最小剩余电量和最大剩余电量；ECmin、ECmax分别为超级电容器储能系统的最小剩余电量和最大剩余电量；EHmin、EHmax分别为氢储能的最小剩余电量和最大剩余电量。氢储能与超级电容器为最大容量的10%与90%，锂电池为最大容量的20%与80%。

2.2.2 集装箱功率密度约束

由于预装式微网储能电站的体积有限，为了能够将多元储能单元合理有序地摆入集装箱，需要对箱体功率密度做约束，使多元储能电站的总体积为

式中，Vtotal为多元储能单元总体积；Pele为所配置燃料电池的容量；ηFc0、ηele、ηC0、ηLi分别为燃料电池、电解槽、超级电容器、锂电池的功率密度；β为根据箱内摆放情况所设置的空间系数。

集装箱的功率密度为

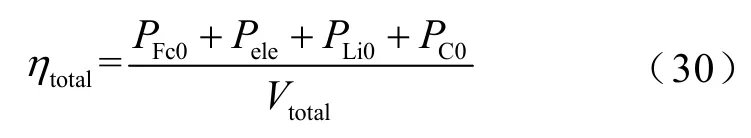
集装箱的功率密度约束条件为

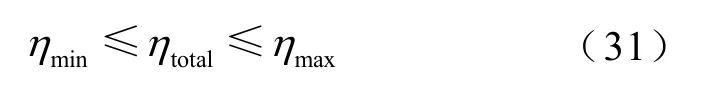
式中，ηtotal为集装箱的功率密度；ηmin、ηmax分别为多元储能单元中的最小、最大功率密度。

2.2.3 供电可靠性约束

储能单元的容量配置过小，会造成负荷缺电量较大，供电可靠性降低；储能单元的容量配置过大，会导致整个系统的成本升高，经济性降低。鉴于此，引入负荷缺电率和能量溢出率的约束条件为

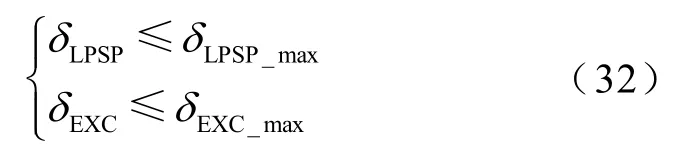
式中，δLPSP_max为负荷缺电率上限；δEXC_max为能量溢出率上限。

2.3 求解方法

预装式多元储能电站容量优化配置的过程是一个非线性、多变量问题的求解过程，采用遗传算法进行求解。以燃料电池额定功率、电解槽额定功率、氢储能的容量、锂电池额定功率与额定容量和超级电容器的额定功率与额定容量为决策变量进行寻优。

3 算例分析

以我国某微电网风电装机容量为3MW、光伏装机容量为 6MW 的风光互补微电网为例进行计算，根据该微电网全年的风电出力、光伏出力和负荷用电需求的历史监测值，优化配置多元储能单元容量。据监测值显示，该微电网负荷峰值为6MW，采样的时间间隔为 36s。采用平均电价折算倍数法来估计缺点惩罚系数及能量溢出惩罚系数，平均电价为0.45元/(kW·h)，缺电惩罚电价倍数取2.7，能量溢出惩罚电价倍数取3.3。系统的相关参数见表1[27,29-30]。

3.1 储能容量配置结果与分析

基于本文所建立的关于多元储能容量优化模型，采用遗传算法优化微电网系统储能容量，误差小于0.01作为运算结束控制变量。对可能出现的七种不同储能组合方案进行了计算，其中，方案1：氢储能、锂电池和超级电容器组合的配置结果；方案2：氢储能单一配置结果；方案3：锂电池单一配置结果；方案4：超级电容器单一配置结果；方案5：氢储能和锂电池组合的配置结果；方案 6：氢储能和超级电容器组合的配置结果；方案 7：锂电池和超级电容器组合的配置结果。所得微网储能容量优化配置结果见表 2。根据许继集团、Maxwell以及Horizon燃料电池集团等生产厂家的数据得出多元储能单元功率密度见表3。

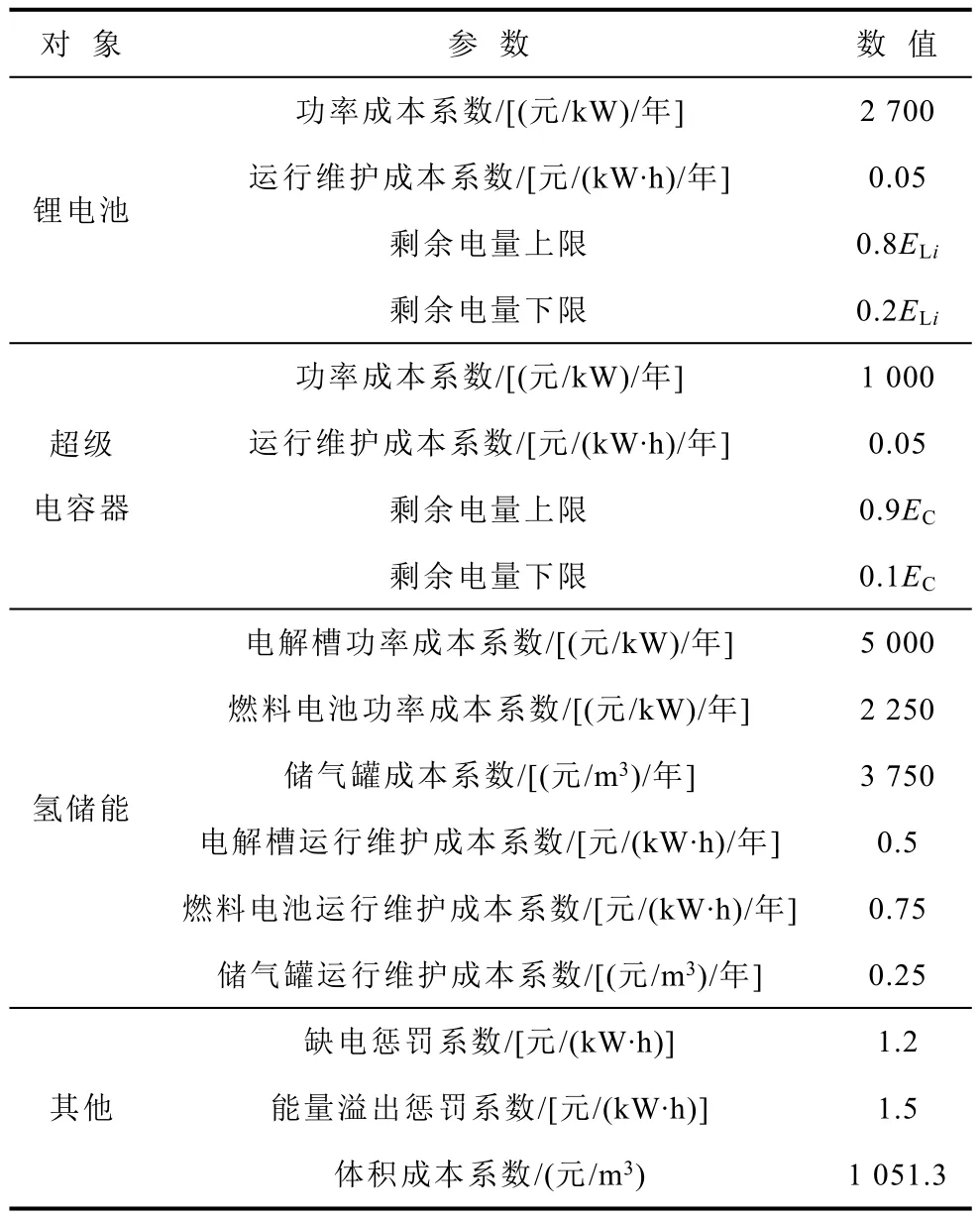
表1 系统相关参数Tab.1 System related parameters

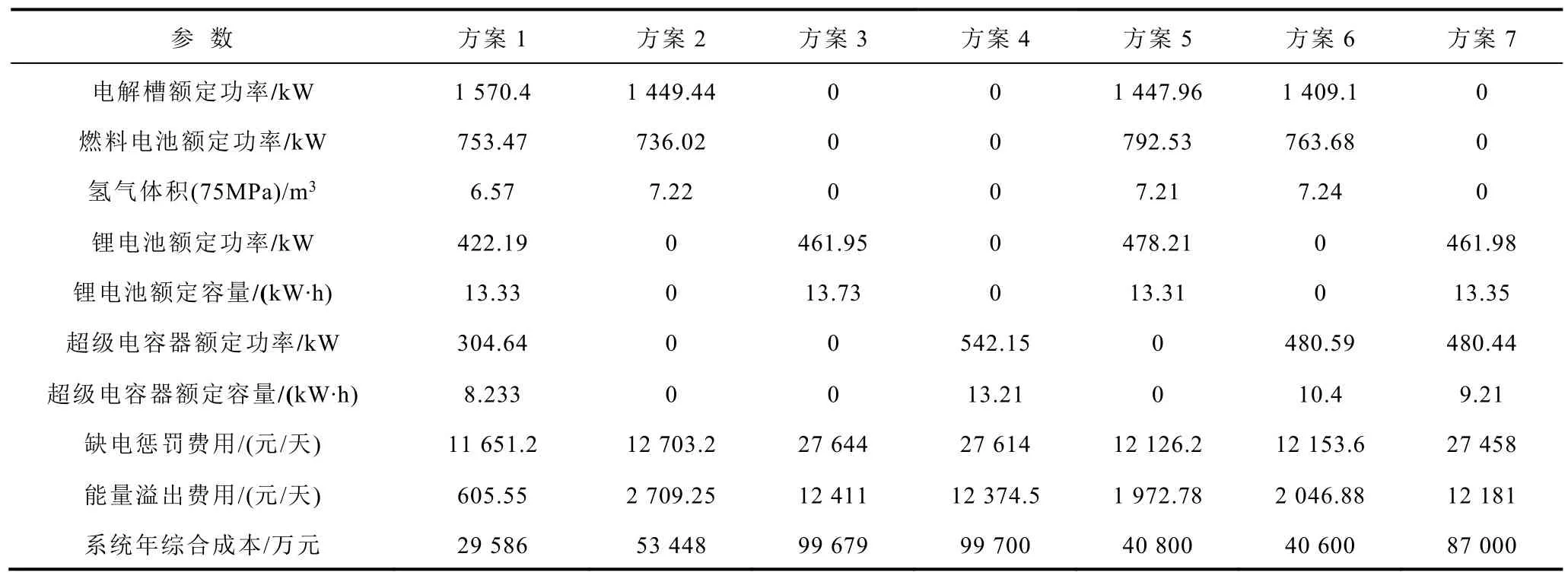
表2 储能容量优化配置结果Tab.2 Optimization result of energy storage capacity

表3 多元储能单元功率密度Tab.3 Power density of multiple energy storage units

由表 2可知，在对比配置方案 2、3与方案 4可以发现，采用氢储能的单一储能单元相较于采用锂电池与超级电容器的单一储能单元，系统的总造价下降了 46.38%与 46.39%，这主要是因为平衡功率中低频分量占比较大，中频和高频分量占比较小，受制于经济技术性能约束，锂电池和超级电容器不用于补偿低频分量，而氢储作为长期能量型的储能具有更强的供电能力和平抑低频分量的作用，使得氢储能相较于锂电池和超级电容器缺电惩罚费用分别下降了 54.05%与 53.99%，能量溢出费用分别下降了 78.17%与 78.11%，从而使得系统的年综合成本大幅度下降，这也印证了引入氢储能的必要性。

通过对比配置方案5、方案6、方案7与配置方案2、方案3、方案4可知，采用混合储能单元代替单一的储能单元，系统的经济性也明显向好，这是因为混合储能单元相较于单一储能单元功能完备，系统的供电可靠性增加，反向吸收溢出能量的能力也增加，使缺电惩罚费用与能量溢出费用降低，进而使系统的年综合成本也大幅降低，这是引入混合储能的原因所在。

配置方案1为包含氢储能、锂电池与超级电容器的多元储能单元的配置方法，通过与配置方案 7仅含锂电池与超级电容器的方法相比较，采用含氢储能的多元储能代替锂电池与超级电容器的混合储能单元配置方案，锂电池和超级电容器的配置规模有所减小，但是增加了氢储能，由于氢储能出色的长期供电能力，使得因为由于引入氢储能所增加的一次投资成本与运行维护成本远远小于缺电惩罚费用与能量溢出费用，使得系统年综合成本降低了66%。

结合表2最终容量配置结果与表3的多元储能单元功率密度可知，方案1所占用的总体积为59.96m3，方案2所占用的总体积为 49.88m3，方案 3所占用的总体积为 8.33m3，方案 4所占用的总体积为0.375m3，方案5所占用的总体积为58.46m3，方案6所占用的总体积为49.16m3，方案7所占用的总体积为 8.64m3。以许继集团标准 40ft(12.032m×2.352m×2.549m)、体积为72m3的集装箱为例，除去检修散热通道、控制系统等占用体积，实际储能系统可用体积约为 30m3，本文所设计方案 1、2、5、6需使用两个集装箱，而方案 3、4、7需使用一个集装箱。

3.2 含氢储能的预装式多元储能电站运行模拟效果分析

由 3.1分析可知，考虑氢储能在内的多元储能相较于传统的锂电池和超级电容器储能在功能上更为完备，经济性能更优，采用该方案可以更好地提高微电网的运行经济性和供电能力。

利用反傅里叶变换针对多元储能单元频谱分析结果进行时域变换，得到平衡功率中低、中、高频功率分布如图4所示。多元储能单元之间的充放电主要取决于平衡功率的波动频率的高低，低频分量用氢储能进行补偿，中频分量用锂电池进行补偿，而高频分量用超级电容器进行补偿。根据初始功率分配结果，为满足峰荷需求将导致储能容量大幅增加，进而使系统经济性受损。因此这里进行功率调整以实现供电可靠性和储能容量的平衡，即在最经济的配置下达到供电可靠性最高。调整后的多元储能功率分配结果分别如图5～图7所示，此时功率大于零表示充电，小于零表示放电，多元储能单元的最大充放电功率有个明显的“剃头”效果，这就是对补偿功率进行功率调整的结果，避免为了某些尖端负荷的供电而无限增加所配置容量的大小，降低了系统的年综合成本，并提高了系统的经济性。

图4 多元储能补偿功率分配Fig.4 Compensation power distribution of multi-component energy storage

图5 调整后氢储能功率分配Fig.5 Power allocation of adjusted hydrogen storage

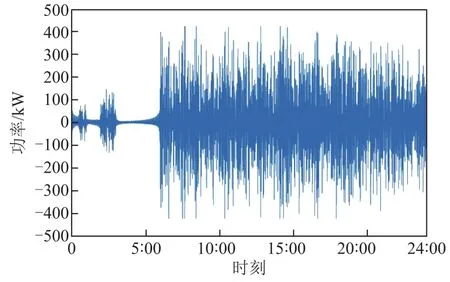
图6 调整后锂电池功率分配Fig.6 Power allocation of adjusted lithium battery

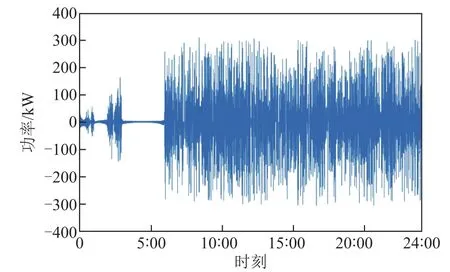
图7 调整后超级电容器功率分配Fig.7 Power allocation of adjusted super capacitor

由图8可知，在微网中接入储能后，平衡功率的波动情况有了明显的改善，正向峰值减小了26.12%，反向峰值减小了72.3%，起到了有效平抑平衡功率波动的作用。正反向峰值差的减小使得平衡功率的充放电由无规则的波动变为均值在零附近波动，使储能系统可以在一天一个周期内基本完成一个完整的充放电，能够有效地提高储能系统的寿命。具体的参数对比见表4。

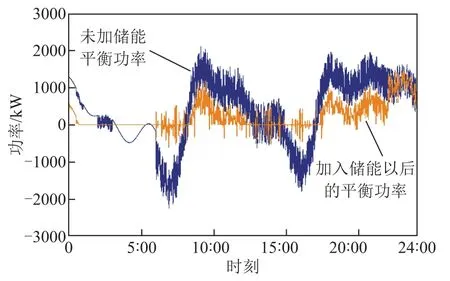
图8 接入储能后的功率变化情况Fig.8 Power change after accessing energy storage

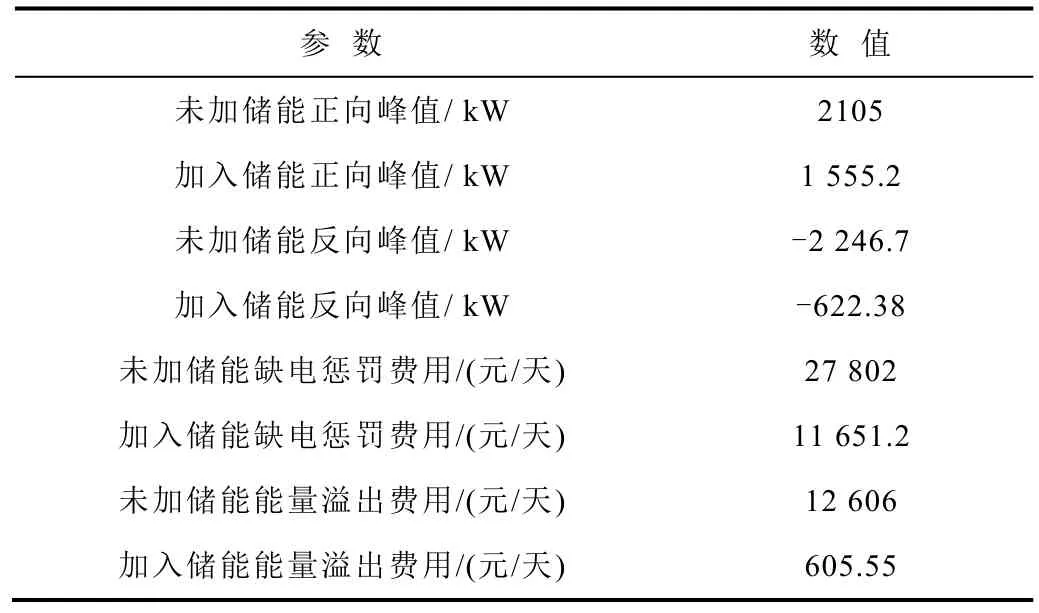
表4 储能容量优化前后参数对比Tab.4 Comparison of parameters before and after energy storage capacity optimization

由表4分析可得，加入储能以后缺电惩罚费用减小了58.09%，有效保证了供电可靠性，避免了因新能源出力无法满足负荷需求而停电造成的财产损失；能量溢出费用减小了 95.2%，避免了能量的过度浪费。本文所提出的多元储能容量优化配置方法的经济性得到了充分证明。

本文分别建立氢储能、锂电池、超级电容器荷电状态曲线如图 9～图 11所示。由图可知，氢储能和超级电容器的荷电状态都可以保持在 0.1～0.9之间，锂电池的荷电状态可以保持在 0.2～0.8之间。避免储能单元的过充或者过放，可以提高储能单元的使用寿命。图9曲线变化平缓，而图10和图11变化相对比较剧烈，这是由于氢储能补偿低频分量，低频分量变化相对平缓，而锂电池和超级电容器补偿的中、高频分量变化相对比较剧烈，是其在短时间内频繁充放电造成的，通过对比观察图 5、图 6和图7也可以得到相同的结论；造成锂电池和超级电容器的荷电状态不断变化的另外一个原因是通过频谱分析可以发现，平衡功率中中频和高频分量占比较小，导致锂电池和超级电容器所配置的容量不大，数量都在 10kW·h左右，这样就会使锂电池和超级电容器的充放电会造成荷电状态的剧烈变化，实践结果与理论分析一致。

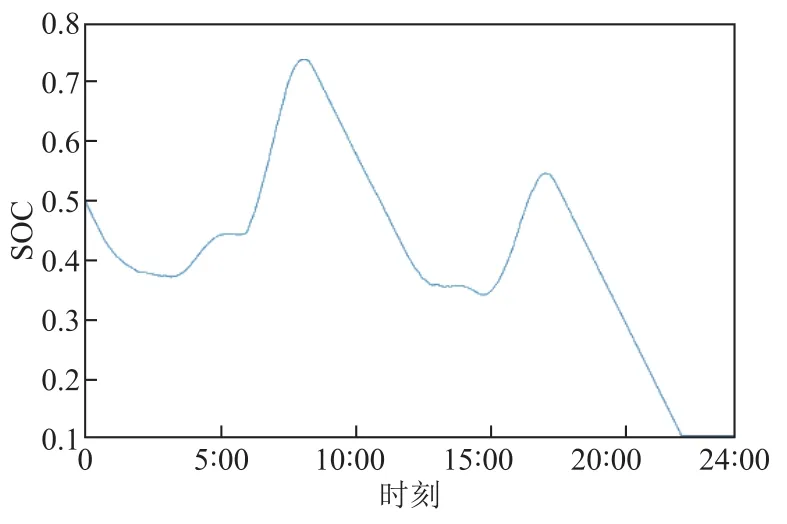
图9 氢储能荷电状态Fig.9 State of charge of hydrogen storage

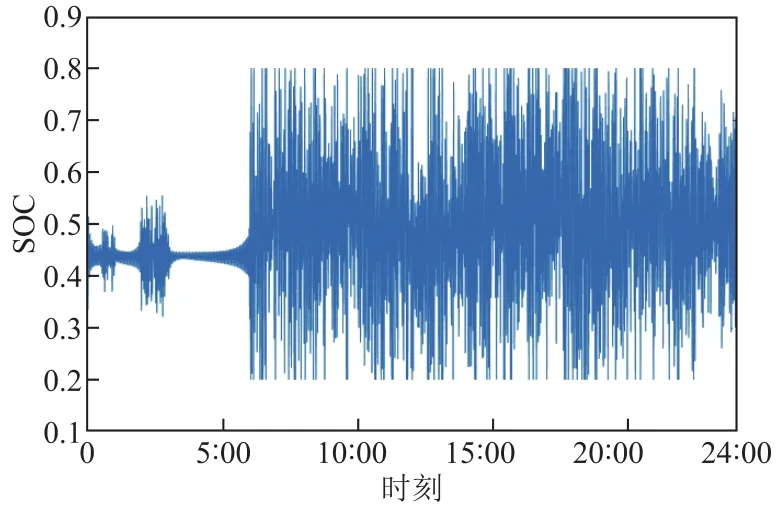
图10 锂电池荷电状态Fig.10 State of charge of lithium battery

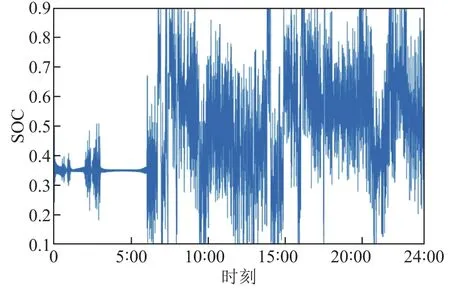
图11 超级电容器荷电状态Fig.11 State of charge of super capacitor

由图9可知，在8:30左右，氢储能的荷电状态达到全天最高的 0.74，这是由于在 3:00～8:30负荷较小，新能源出力较大，造成平衡功率为正，此时储能单元在充电；在 17:00～22:00这段时间，负荷功率大于新能源出力，造成该段时间平衡功率为负，储能单元在不断地放电来维持功率的平衡与负荷之间的匹配。在 22:00时，用于补偿低频分量的氢储能容量达到下限，无法再释放能量，对应图5可以看到，此时氢储能的放电功率为 0。这是对储能单元功率进行调整的效果，用降低一定程度的配置容量来提高整个系统的经济性。

3.3 不同功率密度下配置结果的敏感性分析

为了验证本文配置方法的合理性和经济实用性，本文针对配置方案进行了不同功率密度下配置结果的敏感性分析。系统功率密度的不同，会影响到系统单日缺电惩罚费用和能量溢出惩罚费用，进而影响到储能系统年综合成本的大小。不同功率密度下系统的储能容量配置及系统相关费用如图12和图13所示。

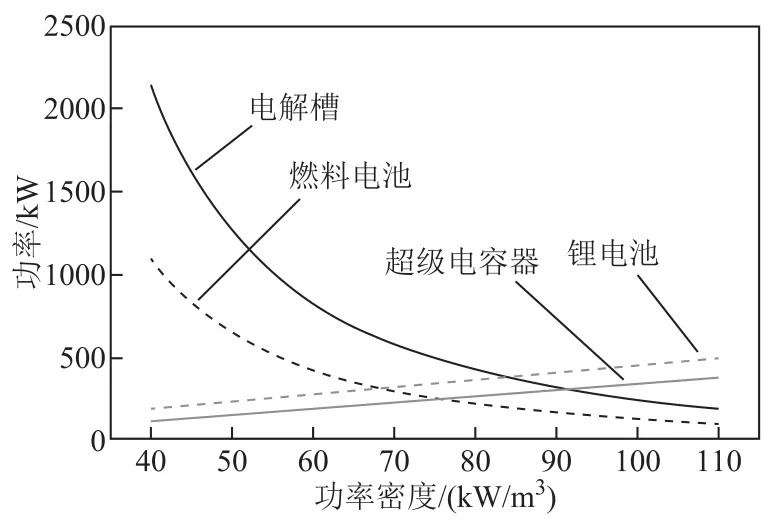
图12 不同功率密度下储能容量配置Fig.12 Energy storage capacity configuration under different power densities

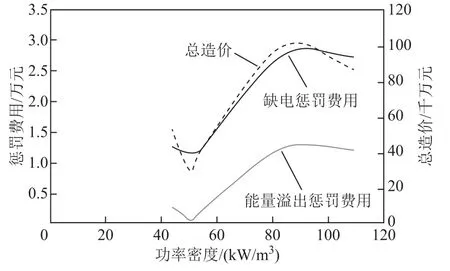
图13 不同功率密度下系统费用Fig.13 System cost under different power densities

由图 12可知，所配置电解槽和燃料电池的功率是随着集装箱功率密度的增大而减小的。锂电池和超级电容器的功率是随着集装箱功率密度的增大而增大的。这是因为集装箱内部是由氢储能、锂电池和超级电容器三种混合储能构成的，导致整个集装箱的功率密度大小是介于最小功率密度电解槽和最大功率密度燃料电池之间的，由于电解槽和燃料电池功率密度小，所占用体积较大；超级电容器和燃料电池的功率密度非常大，所占用的体积较小，但配置的容量与锂电池和电解槽的相差不多，又不足以将集装箱的功率密度提升至一个非常大的量级，所以保持集装箱的功率密度总体保持在40～110kW/m3之间。

由图13可知，随着集装箱功率密度的增大，系统的综合年成本是先减小后增大的，缺电惩罚费用和能量溢出费用趋势相同。这是因为随着集装箱功率密度的增大，氢储能所配置的容量就会减小，使得补偿的低频分量比例小，而低频分量相较于中频和高频所占比重较大，从而造成缺电惩罚费用和能量溢出惩罚费用增大，使系统的年综合成本越来越大。成本最小的点收敛在功率密度为 50.88 kW/m3处，也就是本文所配置的容量，敏感性分析验证了本文所配置容量的经济性。

4 结论

1）本文针对分布式新能源发电系统，构建了由氢储能、锂电池和超级电容器构成的多元预装式储能单元。在对微网平衡功率频谱分析的基础上，提出了基于储能补偿频段特性的系统功率分配策略，通过寻找储能容量和供电可靠性之间的平衡点，引入负荷缺电惩罚费用和能量溢出惩罚费用。以年均总成本最低为目标函数，在剩余电量、能量溢出率、缺电惩罚率及集装箱功率密度等约束条件的约束下，与常规锂电池和超级电容器的混合储能方案相比，含氢储能的多元储能方案在功能和经济方面优势明显。

2）以某一实际微网与许继集团研制的标准集装箱作为算例，去除检修散热通道与控制系统等占用体积，本文设计方案应采用两个标准40 ft的集装箱。为解决远离大电网的偏远地区供电难的问题提供了思路，为相关设备生产厂家提供了借鉴，具有深远的意义。

3）本文在考虑功率密度约束情况下，讨论了含氢储能的多元预装式储能电站的容量配置问题，在实际中可能还需要考虑散热、储能单体的形状等因素对容量配置的影响，将另文研究。