基于样本协方差矩阵特征特性的电网多重扰动定位方法

2021-02-22李洪乾周忠强

电工技术学报 2021年3期

李洪乾韩松周忠强

（1. 贵州大学电气工程学院贵阳 550025 2. 贵州电网有限公司电力调度控制中心贵阳 550002）

0 引言

随着同步相量测量装置、广域测量系统（Wide Area Measurement System, WAMS）的广泛应用以及5G等信息通信技术的快速演进，面向电网状态的随机波动性和复杂耦合性[1]，从数据驱动角度出发，借助大数据技术[2]，将电网量测系统采集的海量电力内外部多源数据进行知识提取和价值应用，或为新一代电力系统安全分析与控制带来新的解决方案和技术路径[3-4]。

在大数据分析方法中，随机矩阵理论（Random Matrix Theory, RMT）以大维统计原理作为根基，从宏观角度反映系统当前运行状态[5]。一方面，在基于RMT的电力系统分析理论与方法研究中，平均谱半径（Mean Spectral Radius, MSR）指标已初步实现对电网异常场景识别[6]、用户窃电侦测[7]和电网扰动传播分析[8]等应用。相较MSR指标，样本协方差矩阵最大特征值（Maximum Eigenvalue of Sample Covariance Matrix，Max-ESCM）指标不仅具备相近功能，且更适用于低信噪比场景[9-10]，在大规模电网中计算效率更高[11]。而基于RMT中的样本协方差矩阵最小特征向量（Minimum Eigenvector of Sample Covariance Matrix, Min-ESCM）指标[12]虽然在数学领域已进行了研究，但目前在电力系统领域还少有探索。另一方面，在基于RMT的电力系统领域应用探索过程中，对电网扰动定位已进行了初步研究。文献[13]基于RMT并结合增广矩阵法提出了一种故障时刻确定和故障区域定位方法，通过分别计算及比较各节点 MSR指标之差，实现了对故障节点的定位。在文献[13]的基础上，文献[14]通过分别构建每条线路的增广矩阵，并对其 MSR指标进行计算及越限判别，从而定位出故障线路。不同于文献[13-14]，文献[15]基于RMT通过不断对电网矩阵进行分块计算并在图形界面中进行对比，实现了对电网扰动区域的定位。然而，随着系统规模的增大，上述文献所需运算次数将大幅增加，导致计算效率偏低。此外，这些文献中，扰动节点是通过指标间比较的方式来定位的。因此，当电网发生多重扰动[16]时，存在难以对其进行有效定位、适应性差的问题。

鉴于此，为了提升 RMT在电网扰动定位应用中的计算效率和适应性，本文基于 Max-ESCM 及Min-ESCM提出了一种适用于多重扰动场景的电网扰动定位方法。借助DIgSILENT和Matlab R2014a软件，通过IEEE 54机118节点系统算例，表明了该方法的有效性和高效性。

1 基于Spiked模型的电网扰动识别

1.1 数据源矩阵的构建与预处理

在广域测量系统中，相量测量单元（Phasor Measurement Unit, PMU）能采集海量具有统一时间戳的电气量测数据[6]。将筛选后的量测数据按照时空特性排列，可构成一个二维矩阵，即数据源矩阵Xs，如式（1）所示。

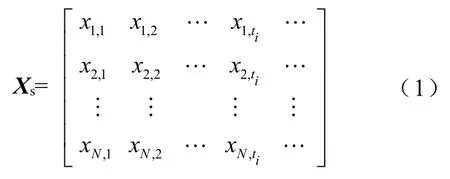
Xs不仅存在随机噪声的干扰，还受到负荷随机波动造成的影响，其检测模型可写为

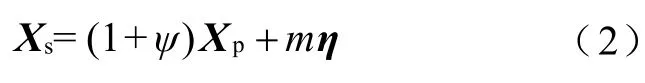
式中，Xp为未受噪声污染的信号矩阵；ψ为负荷随机波动率，波动范围设置为±1%；η为噪声矩阵；m为噪声幅值。

得到Xs后，对其采用滑动窗口技术可得N×T维窗口数据矩阵X，并将X的行向量按式（3）进行标准化处理，得到标准非Hermitian矩阵Xn。

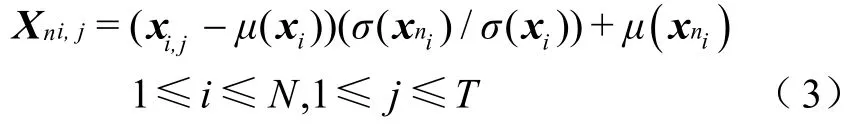
式中，xi=(xi,1,xi,2,…,xi,T)；μ(xi)、σ(xi)分别为xi的均值和标准差；μ(xni)、σ(xni)分别为非 Hermitian矩阵行向量xni的均值和标准差。

1.2 基于Marčhenko-Pastur定律的扰动识别

RMT中 M-P定律（Marčhenko-Pastur law）[17]对大维样本协方差矩阵的渐进谱分布特性进行了描述。采用M-P定律可对经过预处理后的电网量测数据矩阵进行分析。当电网中无扰动事件发生时，各节点采集的量测数据整体相对平稳且具有一定随机性，此时其 Max-ESCM指标也将满足其统计规律，收敛于一定范围。但若电网中出现负荷突变或线路故障等扰动情况，则采集的量测数据将发生突变而且系统的随机性也会被破坏，导致Max-ESCM指标越过其正常统计边界。因此，可以利用该定律识别电网中扰动事件的发生。对于M-P定律[17]的原理与方法描述如下。

设Xn={xi,j}1≤i≤N,1≤j≤T为一个N×T维的随机矩阵，且每个元素满足独立同分布。当µ(x)=0，σ2(x)＜∞时，则Xn的N×N维样本协方差矩阵S为

式中，上标H表示共轭转置。此时，样本协方差矩阵S也为实对称矩阵，当维容比c=N/T∈(0,∞)不变时，S的经验谱密度将收敛于M-P律，谱密度函数可表示为

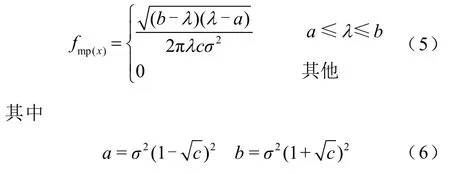
式中，σ2为刻度参数，σ2=1；a和b分别为谱密度函数中特征值的理论下、上确界。

1.3 基于Spiked模型的Max-ESCM动态阈值

传统M-P律中，阈值采用的是式（6）中的边界值，但该边界值a与b仅与矩阵的c有关，而忽略了样本所受到的干扰，故该边界值存在一定的局限性。因此，为了增强对扰动事件判定的适应性，本文采用前期研究中基于 Spiked模型的动态阈值[9]，对 Max-ESCM指标进行越限判别。该动态阈值在传统阈值模型的基础上，进一步考虑了样本所受干扰的影响，增强了扰动识别的适应性，其具体表达式为

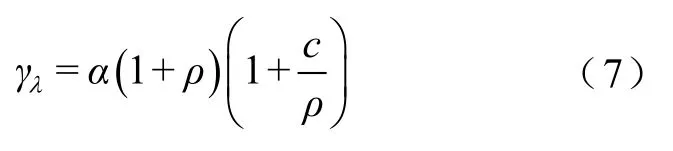
式中，γλ为Max-ESCM指标的动态阈值；ρ为当前时刻全局信噪比估算值；c为维容比；α为比例系数，0≤α≤1，可根据滑动窗宽度T进行调整[9]，一般取α=0.5。

2 基于“相变”现象的电网多重扰动定位

2.1 多重扰动

电力系统是复杂的非线性时变系统，在运行过程中会不可避免地受到一系列扰动，使其结构发生改变、潮流重新分配，甚至导致系统失稳[18]。虽然电网中发生多重扰动的概率较低，但若仅针对电网单一扰动进行分析是不全面的。因此，从多重扰动观点出发研究电网扰动定位是有必要的，并且这也更能反映实际电网扰动事件的随机性和突发性。

电网中多重扰动是由引起系统运行状态变化的多个事件在时间、空间、类型上组合而成[16]。根据时间先后发生顺序可分为一个节点发生扰动，另一个节点也在相隔较小的时间内发生扰动的同时多重扰动，以及一个节点扰动形成后，影响或传播到其他节点也发生扰动的相继多重扰动。

2.2 基于Min-ESCM的多重扰动定位

识别出电网有扰动事件发生后，对所有扰动源进行快速定位对电网安全运行具有重要意义。区别于传统模型驱动的电网扰动定位方法，基于 Min-ESCM的电网多重扰动定位方法是一种数据驱动的方法，其具体原理如下。

对于任意一个样本协方差矩阵S，其主对角线呈自相关，副对角线呈互相关。进行特征分解可得

式中，v为矩阵S的特征向量；λ为矩阵S的特征值。

根据定理[19]：设A=(aij)N×N是非负不可约矩阵，v=[v1v2…vn]T是一个正向量，令Xij=aijvj/vi(Xij≥0)，若则λ是A的模最大特征值，结合式（8）可得[20]

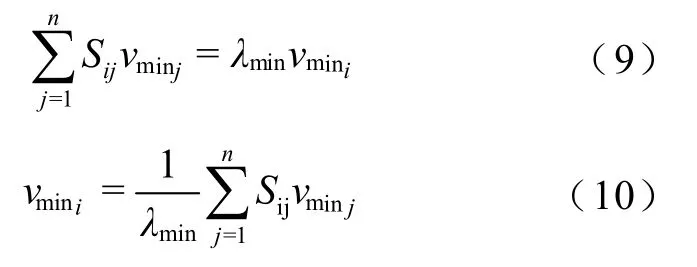
由式（10）可知，在矩阵S的vmin中，vmin的第i个元素vmini的变化主要与矩阵S的第i行有关联。当矩阵S的第i行出现波动时，将导致vmin上第i个元素的值出现显著变化，且与其他元素有明显区别。因此，对于由电网量测数据处理得到的样本协方差矩阵，当电网中出现扰动时，扰动节点k、l…的数据将出现波动，这时将导致Min-ESCM指标中第k、l…号元素的数值相较于其他元素出现显著变化。故可依据该原理对电网多重扰动事件进行快速定位。

2.3 基于“相变”现象的Min-ESCM动态阈值

“相变”现象原指物理系统中的临界现象，当物质达到某临界点时，将会从一种状态转换到另外一种状态。而对于大维实对称矩阵的特征向量，当对应特征值达到一定范围时，该特征向量中各元素将呈现出特定的分布规律，在数学领域上称其出现了“相变”现象[12,21-23]。

假设c∈(0, 1]，有一N×1维单位向量ek，其中仅第k个元素的值为1。当矩阵S的特征值处于不同范围时，对应特征向量将收敛于[12]

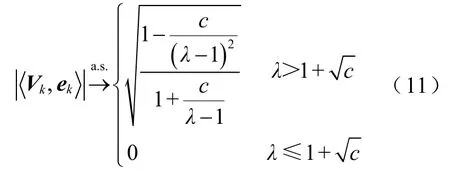
式中，γv为Min-ESCM指标中每一个元素的阈值，当Min-ESCM指标中第k、l…号元素的值大于γv时，说明系统受到的扰动是由第k、l…节点引起的；β为比例系数，0≤β≤1，可根据滑动窗宽度T进行调整[9]，一般取0.5。

3 所提方法流程图与步骤

电网多重扰动定位方法流程如图1所示。具体步骤如下：

1）由式（1），将PMU采集的量测数据构造为数据源矩阵Xs。如为模拟现场信号，可通过式（2）引入噪声和随机波动负荷。

2）根据式（3），对矩阵Xs进行预处理后，结合式（4）获取其N×N维样本协方差矩阵S。

3）计算S的最大特征值λmax并将其作为扰动识别指标Max-ESCM。

4）由式（7）计算当前时刻 Max-ESCM 基于Spiked模型的动态阈值γλ。

5）判断λmax≥γλ是否成立，若成立，则判定电网有扰动事件发生，需进一步对其进行定位并执行步骤6），否则重复步骤2）～步骤5）。

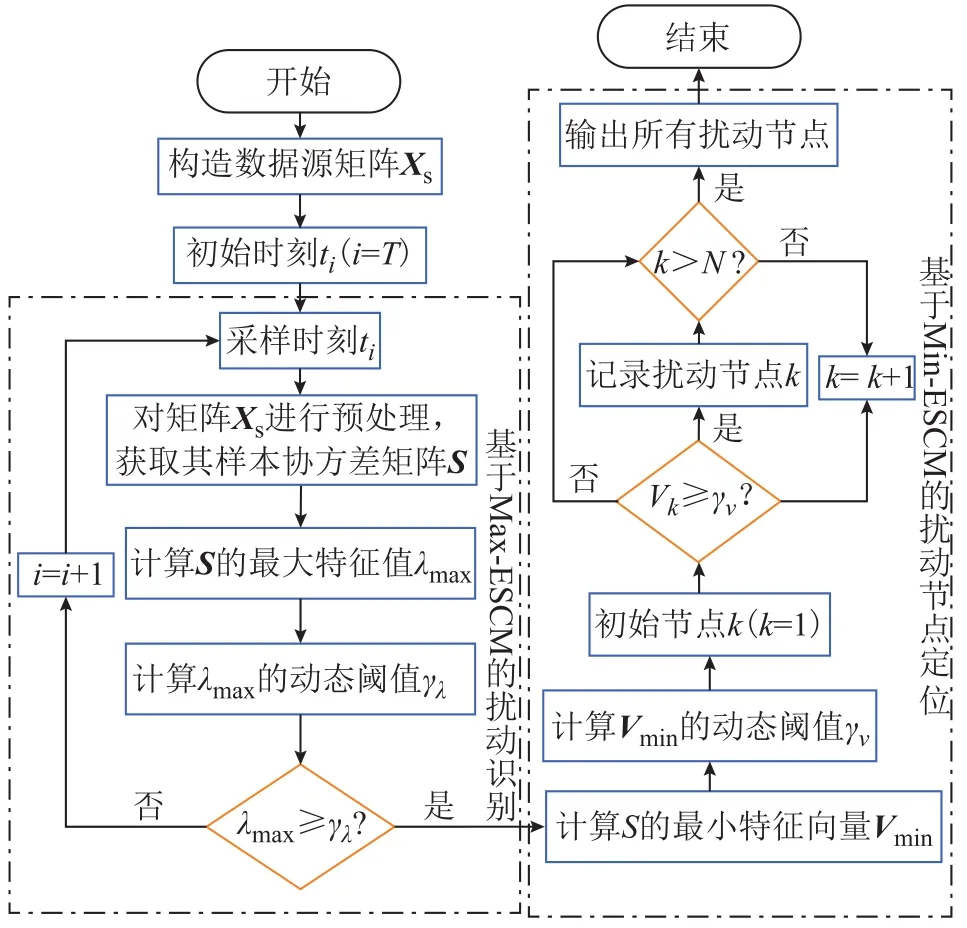
图1 所提电网多重扰动定位方法流程Fig.1 The flowchart of the proposed multiple disturbance positioning method for power system

6）计算扰动定位判别指标Min-ESCM即Vmin。

7）根据式（12）计算Vmin基于“相变”现象的动态阈值γv。并设置初始节点k=1。

8）判断Vk≥γv是否成立，其中Vk为Vmin中第k个元素，若成立，记录引起扰动事件的节点k，并进行步骤9），否则直接进行步骤9）。

9）判断k＞N是否成立，若成立，输出所有扰动节点编号，否则k=k+1并回到步骤8）。

4 算例分析

借助DIgSILENT软件，对如图2所示的IEEE 54机118节点系统[24]开展时域仿真获取测试数据，其中仿真步长均为Δt=0.01s。依据第3节方法步骤在 Matlab R2014a软件中编制算法程序，以验证本文所提多重扰动定位方法的有效性。

4.1 同时多重扰动定位测试

为模拟电网中同时多重扰动场景，设置节点21与相隔较远的节点 95在t1001采样时刻同时出现负荷跃变，具体见表1。

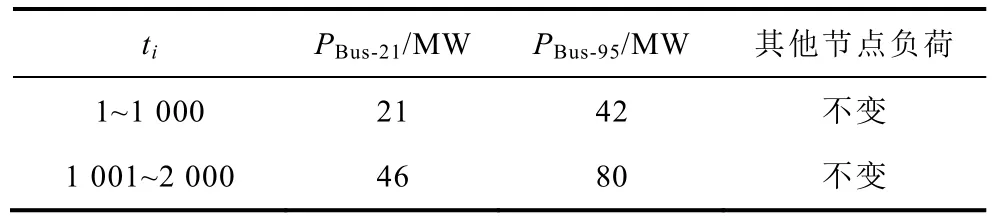
表1 一类同时跃变的合成负荷Tab.1 The synthetic loads with simultaneous step-up change

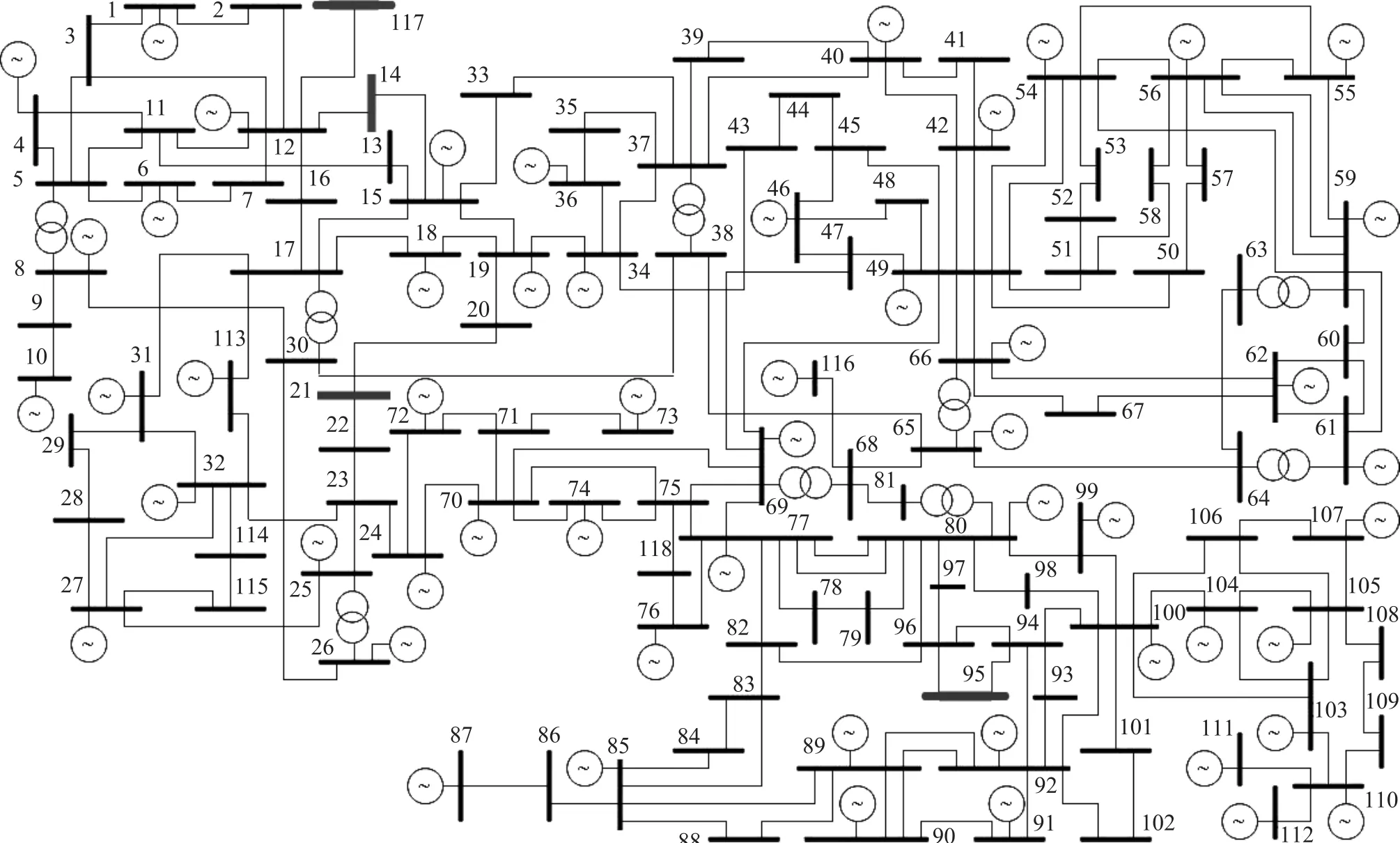
图2 IEEE118节点测试系统Fig.2 IEEE 118-bus test system

按照第3节步骤1），选取全网118个节点的电压幅值作为数据源进行测试。为模拟PMU量测数据中噪声干扰和随机负荷波动，在该信号中引入高斯噪声源[10]。这样可由式（1）和式（2）构建一个118维数据源矩阵进行分析。由步骤 2），设滑动窗口宽度T为240，则Max-ESCM指标变化曲线从采样时刻t240开始，此时维容比c=0.5[13]。将118×240维窗口矩阵按式（3）标准化后，根据式（4）获取其样本协方差矩阵。进一步地，由步骤3）和步骤4），可分别获得当前时刻Max-ESCM指标及其对应动态阈值。

依次对不同时刻滑动窗口数据进行计算，得到t240～t2000采样时刻的Max-ESCM指标及其对应动态阈值曲线，如图3所示。由图3可知，在t1000采样时刻之前，虽然受到了随机负荷的波动及噪声的干扰，但Max-ESCM指标无明显变化。然而在t1001采样时刻，图3中Max-ESCM指标由2.89近似阶跃地增加至 15.09并越过当前时刻阈值，说明电网当前有扰动事件发生，这可能与所设节点 21和节点95有功负荷突变有关。因此，依据步骤5），需对引起该事件的扰动节点进行快速定位。

图3 Max-ESCM指标计算结果Fig.3 The results from Max-ESCM

由步骤6）与步骤7），计算Min-ESCM及其对应阈值γv。然后，根据步骤8）与步骤9），对当前时刻Min-ESCM指标中的每个元素进行判断，输出所有大于其动态阈值的元素，即为引起该扰动事件的节点编号，如图4所示。

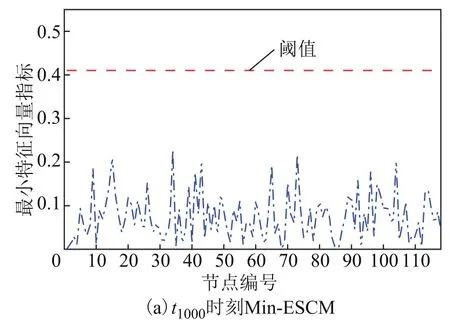
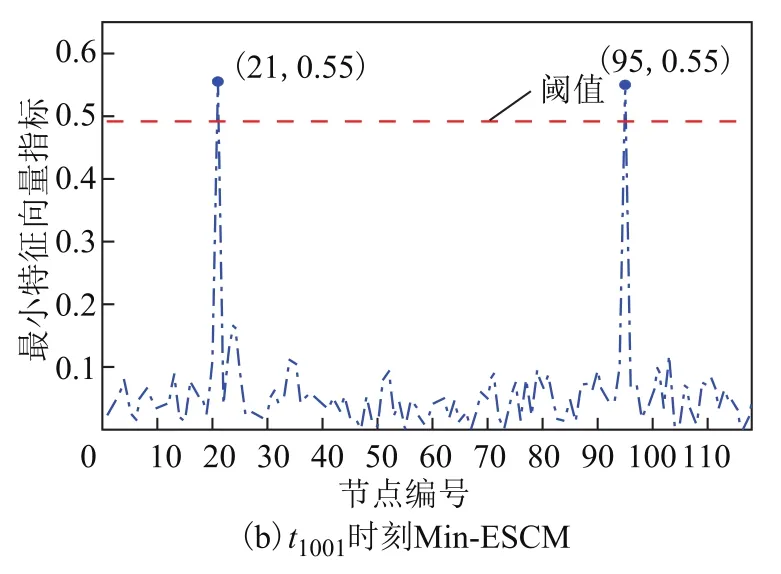
图4 Min-ESCM指标计算结果Fig.4 The results from Min-ESCM

对比图4a与图4b可知，在t1000采样时刻，因电网中没有扰动事件发生，所以Min-ESCM指标中各元素分布相对随机均匀，且均未超过对应阈值。但在t1001采样时刻，因电网中有扰动事件发生，使得系统随机性被破坏，此时Min-ESCM指标中的第21号元素与第 95号元素的数值相较于其他元素出现了显著变化，并且超过了当前阈值，故可判定引起该事件的扰动节点编号为 21与 95，这与实际设置的扰动情况一致。因此，这说明了本文所提方法对电网同时多重扰动定位是有效的。

4.2 相继多重扰动定位测试

对于相继多重扰动场景的模拟，分别设置了“滑动窗内”场景，即节点117与相邻节点14在间隔一个滑动窗内相继出现有功负荷跃变，和“滑动窗外”场景，即节点117与节点14在间隔一个滑动窗外相继出现有功负荷跃变，见表2。

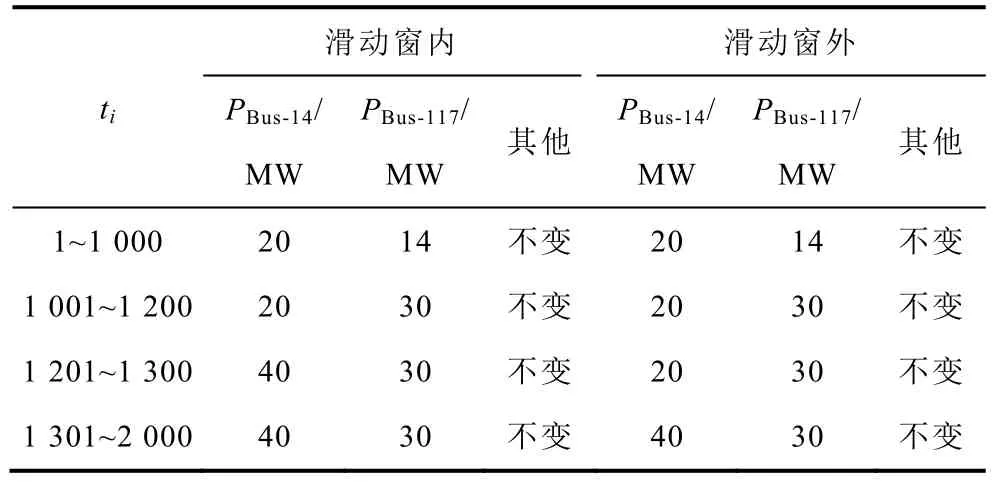
表2 一类相继跃变的合成负荷Tab.2 The synthetic loads with successive step-up change

按照第 3节扰动识别的步骤，可分别得到上述两种场景下Max-ESCM指标的变化曲线，如图5所示。由图5a与图 5b可知，在扰动时刻Max-ESCM指标的值均超过了当前阈值，说明系统此时有扰动事件发生，需进一步对扰动节点进行定位。此外，在再次出现扰动事件的时刻，Max-ESCM曲线均又一次出现了波动，且波动点发生时刻与相继扰动发生时刻几乎一致。因此，可判断此时存在相继扰动事件。

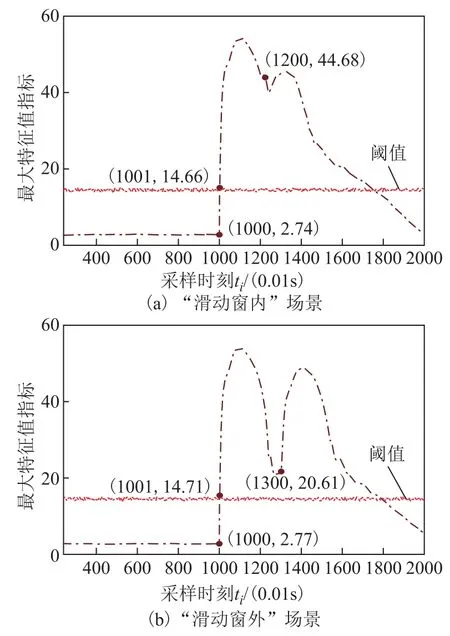
图5 Max-ESCM指标计算结果Fig.5 The results from Max-ESCM

根据第3节扰动节点定位的步骤，可分别得到上述两种场景下Min-ESCM指标的变化曲线，如图6所示。从图6a与图6b可知，在t1001采样时刻，两种场景下的Min-ESCM指标中均仅有第117号元素大于当前时刻动态阈值，这表明该方法能够对电网首先发生的单一扰动事件进行有效定位。

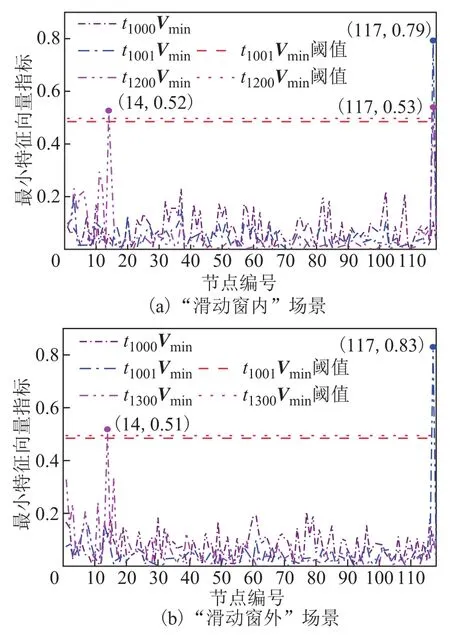
图6 Min-ESCM指标计算结果Fig.6 The results from Min-ESCM

其次，对比图6a与图6b可得，当相继多重扰动发生时刻大于或小于时间窗时，Min-ESCM指标在同一时刻将出现不同现象。对于“滑动窗内”场景，由于 14号节点有功负荷在相隔 200采样时刻之后发生了跃变，其相继扰动发生时刻小于一个滑动窗宽度，此时 Min-ESCM指标中的14号元素与117号元素在t1200采样时刻均超过了当前阈值，故可判断出 14号节点此时有扰动事件发生。而对于“滑动窗外”场景，因为14号节点有功负荷相隔300采样时刻之后才发生了跃变，其相继扰动发生时刻大于一个滑动窗宽度，故在t1300采样时刻的 Min-ESCM指标中仅有14号元素出现突变，从而定位出14号节点此时有扰动事件发生。可见该方法能够有效地定位电网相继多重扰动。

4.3 多重短路故障定位测试

设置节点21与相隔较远的节点95在采样时刻t1001发生了三相短路，故障持续时间为0.49s。采样时刻为t1050后，系统恢复正常，共2 000个采样时刻。根据第3节扰动识别的步骤，可得该场景下Max-ESCM指标的变化曲线，如图7所示。

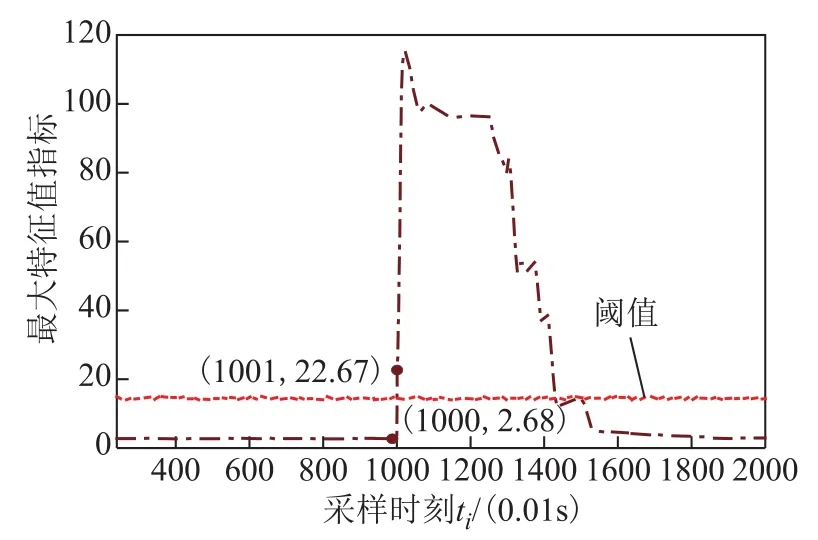
图7 Max-ESCM指标计算结果Fig.7 The results from Max-ESCM

由图7可见，在t1001采样时刻Max-ESCM指标达到了22.67且越过了当前时刻阈值。依据第3节步骤 5），可判断出系统当前时刻有扰动事件发生，需对引起该扰动事件的节点进行快速定位。由第 3节扰动定位的流程可得图8。

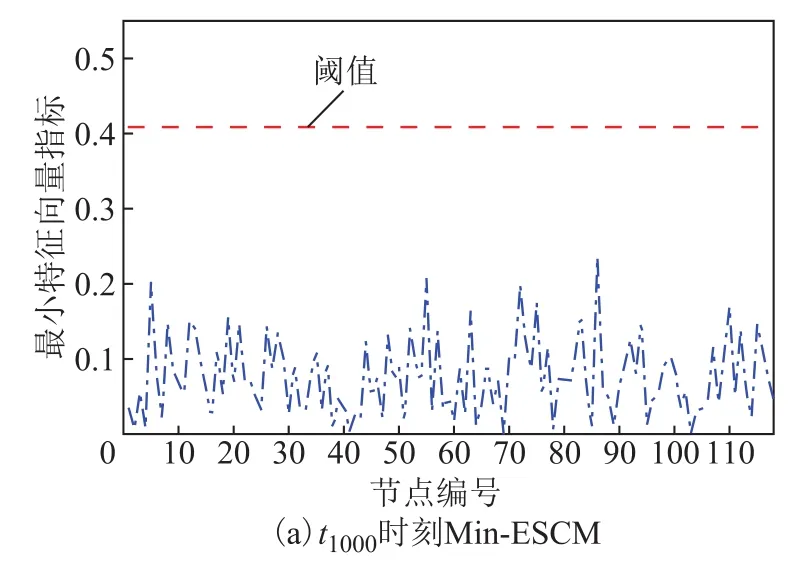
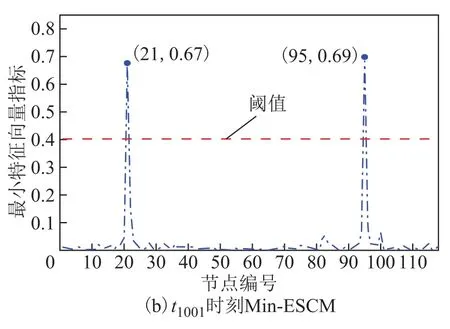
图8 Min-ESCM指标计算结果Fig.8 The results from Min-ESCM

观察图8a与图8b可得，Min-ESCM指标中的第21号元素与第95号元素在t1001采样时刻的数值明显与其他元素不同（其他元素均小于0.1），而且超过了当前阈值。这与实际设置的扰动节点情况一致，可见所提方法对多重短路故障事件定位是有效的。

5 讨论

为支撑本文所提方法的潜在应用，对 PMU信号的时间延迟问题，以及 PMU数据的时效性和空间位置的关联性对电网多重扰动识别和定位的事前辅助可行性讨论如下。

1）关于PMU信号的时间延迟问题。由于PMU发送数据延时抖动、通信协议、通信链路、传送距离、通信链路的负载情况、通信通道带宽等因素的影响，上传到调度控制中心的 PMU实测数据的延时变化范围较大，具有一定的分布特性，一般在几十毫秒到几百毫秒之间变化[25]。针对该问题，一方面，从时间维度来看，可考虑数字信号处理方法来处理，例如：由于不同PMU数据的等效采样频率可能不同，可以认为等效采样频率低的数据类型在采样间隔内数值相等[26]；另一方面，从空间维度来看，可考虑文献[11]所提分区并行计算策略，一个省级或地市级电网范围内设置一个分区子站，一个大区或省级电网范围内设置一个主站，以减少通信距离，降低时间延迟范围。

2）PMU数据的时效性和空间位置的关联性对电网多重扰动识别和定位的事前辅助是可行的。一方面，基于实时数据的阈值设定是电网多重扰动识别的一个关键因素。传统上，基于RMT的扰动识别与定位方法的研究中，其判据一般均采用静态阈值，即往往仅考虑理论模型数据或工程经验。文献[9,27]综合 PMU历史数据和实时数据的动态阈值或许更为合理有效。因此，可以认为PMU的时效性有助于动态阈值的快速生成[11]，继而有助于电网态势感知有效性的提高[28]。另一方面，基于空间位置的分区预警是电网多重扰动识别和定位的一个重要环节。文献[29]指出，不论是单一扰动还是复杂扰动都可能包含传导型关系。复杂扰动在发展过程中同时跨越多个行政区域的情况较少，体现出区域电网间较强的抗扰动能力。这与文献[11]一致。因此，可以认为利用 PMU空间位置的关联性，能够有助于对此类扰动提前预警。此外，需要注意的是，相对传统的离线静态分区预警，结合 PMU数据的在线动态分区预警也是一个值得关注的领域。