基于分布式协同的双极直流微电网不平衡电压控制策略

2021-02-22杨美辉周念成王强钢廖建权孟潇潇

电工技术学报 2021年3期

杨美辉周念成王强钢廖建权孟潇潇

（输配电装备及系统安全与新技术国家重点实验室（重庆大学）重庆 400044）

0 引言

光伏、储能等直流型分布式电源的增加促进了直流微电网的发展[1-3]。相比于交流微电网，直流微电网具有结构简单、控制容易、供电容量大、电能质量高等优点[4-6]。根据是否存在中线，可将直流微电网分为单极和双极直流微电网[7]。相比于单极直流微电网，双极直流微电网提供更多电压等级接口，电压等级可灵活变换，同时其对 AC-DC变换器的利用率高[8]。此外，当某一极发生故障时，另一极可继续保持运行，系统具有更高的可靠性和安全性。但正、负极的电源，负荷和线路参数等不平衡会在中线产生不平衡电流，进而增加线路损耗，同时使正、负极母线电压偏离额定值[9-10]。当某一节点的负荷严重不平衡时，不平衡度可能超标，甚至触发中线的不平衡电压保护[11]。为灵活调节双极直流微电网的电压不平衡度，同时使母线电压运行在合理范围内，须采取一定的分布式协同控制策略，保证直流负荷的正常运行。

针对双极直流微电网的不平衡电压抑制，目前主要有三种策略[12]：①采用可抑制不平衡电压的AC-DC变换器；②在AC-DC变换器的出口安装电压平衡器；③采用负荷切换开关调整直流负荷的供电极性。文献[13-14]提出了在双极直流微电网中，采用三电平变换器抑制直流母线不平衡电压的控制方法，使直流母线的正、负极电压达到平衡的同时，实现电网的双向潮流。文献[15]和文献[16]分别针对单端、多端直流微电网，提出了基于电压平衡器的不平衡电压抑制方法，并验证了所提电压平衡器优异的双极母线调压效果。文献[17]针对双极直流配电网，提出了一种基于负荷开关在线切换的不平衡电压抑制策略，该策略比较初始状态以及负荷开关切换后各节点的不平衡中线电流的大小，确定直流负荷的供电极性，进而在不影响直流负荷电能质量的前提下抑制不平衡电压。由以上分析可知，双极直流微电网的不平衡电压的抑制可从源侧和网侧出发，通过增加不平衡补偿控制环节减小不平衡电流引起的线路损耗和电压偏差，但均只考虑单个变换器的不平衡电压抑制，而未考虑不同节点变换器间分布式电源参与不平衡度调节的协调能力。因此应进一步研究双极直流网络中不同节点变换器母线电压及不平衡度的协调控制，当负载和供电功率在大范围变化时，保证系统稳定运行。

基于一致性理论的分布式协同控制策略结合了集中式控制和分散式控制的优点[18-19]，有利于协调多个变换器的不平衡电压控制。在直流微电网中各单元能够依据自身和相邻单元的信息实时更新自身状态，共同完成协调控制[20-21]。文献[22]提出了基于一致性理论的单极直流微电网多路直流电力弹簧分布式协同控制策略。该策略不仅实现了平均直流母线电压的一致，还保持了储能电池的荷电状态（State of Change, SOC）平衡。文献[23]提出了基于一致性理论的多组混合储能控制方法，不仅有效提升了直流母线电压水平，还实现了不同类储能间的功率分配。文献[24]提出了基于有限时间一致性理论的分布式协同控制策略，实现了直流微电网的电压稳定以及发电成本最小等多目标控制。文献[25]针对含有容性负载的直流微电网，基于一致性理论建立了容性负载电压观测器，实现了微电网的负载均衡控制。文献[26]在实现直流母线电压均值维持在额定值的基础上，提出了一种PI一致性控制电压优化策略，保证了各直流微电网中母线电压偏离额定值的偏差和最小。以上研究均针对单极直流微电网中不同变换器间的协调控制，而未考虑双极直流微电网结构。双极直流微电网因其系统结构中含有中性线，极间电压不平衡成为其特有的电能质量问题，负载功率、网络结构参数等电气量的不平衡及中线阻抗上的压降均会使正、负极电压进一步偏离额定值，从而对直流母线电压偏差补偿及双极直流微电网的功率分配产生影响。因此针对双极直流微电网，还需设计专门的极间不平衡电压控制器，控制正、负极电压的不平衡度在合理范围内，才能保证系统的稳定、可靠运行。

本文将一致性理论应用到双极直流微电网的不平衡电压控制中，通过对多个分布式电源变换器的分布式协同控制，实现双极直流微电网的不平衡电压控制。文中在双极直流微电网的一次控制中采用电压下垂控制，同时根据一致性理论，结合电压不平衡度与正负极电压之间的关系，提出双极直流微电网的分布式协同控制策略。通过设计不平衡电压观测器和不平衡度控制器，使母线电压维持在额定值，并实现了极间电压不平衡度趋于一致。通过对系统进行稳定性分析，从理论上验证了所提控制策略的稳定性和可靠性。最后在Matlab/Simulink中建立双极直流微电网仿真模型，并搭建实验平台，仿真及实验结果表明所提控制策略不仅在电网常规运行中有效，在负载变化和通信网络变化时同样具有良好的有效性。

1 双极直流微电网结构及建模分析

1.1 系统建模

本文研究的双极直流微电网结构如图1所示。该网络包含物理层和网络层，其中物理层包括分布式电源（DG）、直流变换器（DC-DC）、低压直流负载及正线（P线）、中性线（O线）和负线（N线）三条直流母线。DG经由DC-DC变换器接入直流母线，低压直流负载接在PO或NO之间。DG及DCDC变换器在实现传统稳压功能的基础上，还可抑制由于电源和负载不平衡导致的功率波动，并减小不同扰动对系统电压质量的影响。网络层可方便多个直流变换器进行信息交换，在电压不平衡度一致性控制中，将正极和负极相对应的直流变换器视为同一个节点，而在母线平均电压控制中将正、负极的直流变换器视为不同节点。各节点间通过稀疏的通信网络连接，并与相邻节点交换控制变量的信息，更新自身控制信息，达到控制变量的全局一致性。

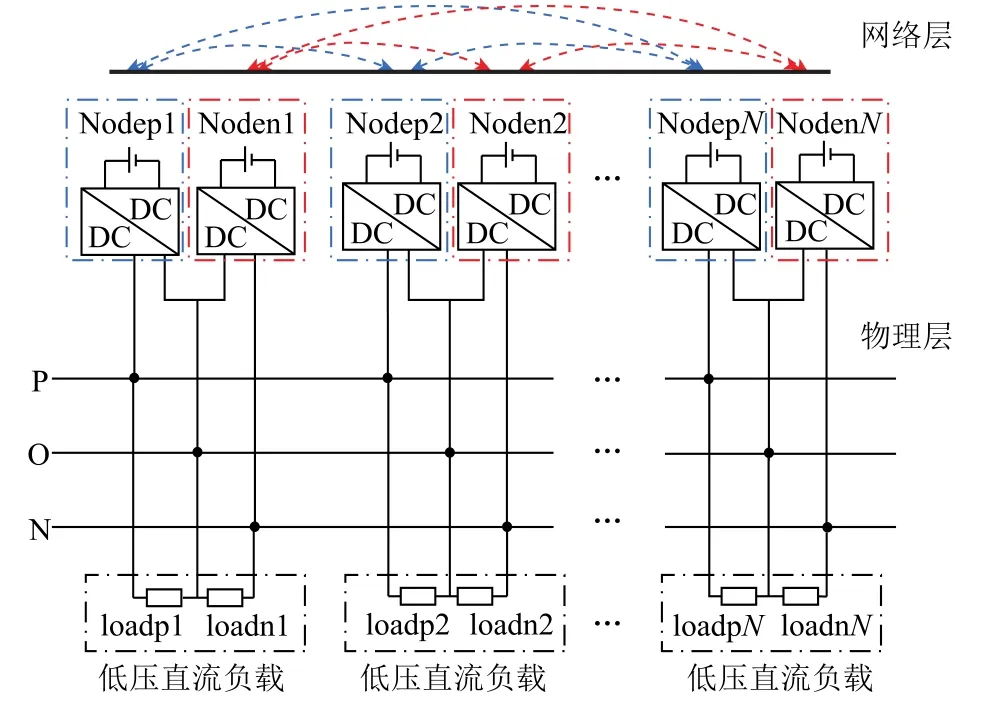
图1 双极直流微电网结构示意图Fig.1 The schematic diagram of bipolar DC microgrid structure

1.2 不平衡电压分析

当正、负极负荷功率不相等时，正、负极电压会产生偏差，即电压不平衡。不平衡度是评估双极直流微电网电压不平衡的一项指标，若电压不平衡度超出设定范围，可能导致微电网运行损耗增加，同时影响直流负荷的正常工作。为保证双极直流微电网的稳定运行，根据ANSI C84，建议将电压不平衡度限制在3%以内[6,27]，文献[6,27]中定义第i个节点的电压不平衡度为

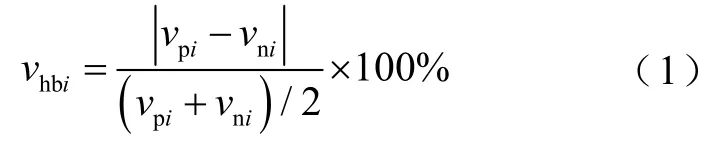
式中，vhbi为第i个节点的不平衡度；vpi、vni分别为正、负极母线电压，下标p、n分别为正、负极。

为进一步分析电压不平衡度与双极直流微电网中系统参数的定量关系，得到正、负极输出电压变化与不平衡度的关系，文献[16]对恒阻抗负载和恒功率负载均进行了不平衡电压分析。本文以恒阻抗负载为研究对象，采用图2所示的简化模型进行分析。

图2 双极直流微电网简化模型Fig.2 Simplified model of bipolar DC microgrid

该简化模型中节点电压和电流满足

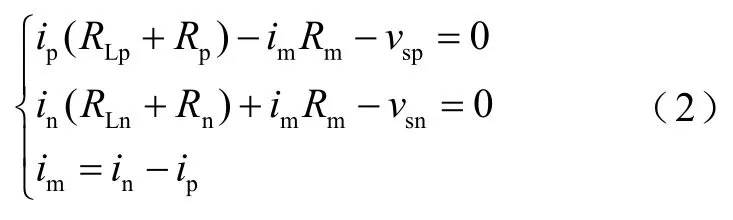
式中，Rp、Rn分别为正、负极负载；RLp、RLn、Rm分别为正极、负极、中线线路电阻；ip、in、im分别为正极、负极、中线电流；vsp、vsn分别为正、负极输出电压。在本文中正、负极线路阻抗相等，即RLp=RLn=RL。

求解式（2），可得不平衡度与负载、中线电阻及正、负极电源电压的关系为

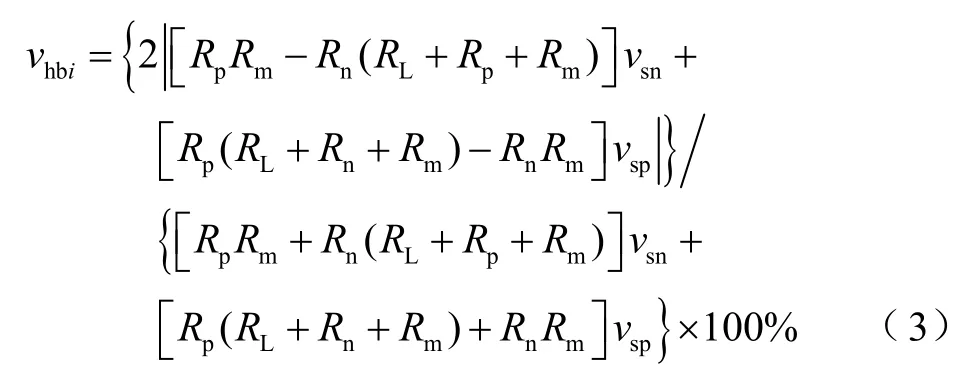
令Rp=20Ω，Rn=10Ω，本文双极直流微电网母线电压的参考值为 400V，为保证电压的合理性，使正、负极电源电压分别在380～420V之间变化。根据式（3），得到双极直流微电网电压不平衡度随正、负极输出电压变化的三维图，如图3所示。

由图3可知：正、负极输出电压平衡时，极间电压不平衡度较小，但随着输出电压不平衡增大，电压不平衡度随之增大，甚至超出ANSI C84建议限定范围的3%，影响双极直流微电网的稳定运行。为保证双极直流微电网电压不平衡度在允许范围的3%以内，正、负极电压应在一定范围内，如图3中x-y平面阴影部分所示。可以设计相应的分布式协同控制策略，合理调配不同分布式电源参与不平衡度调节，同时调节正、负极输出电压，将电压不平衡度控制在合理范围或某一限定值。

图3 电压不平衡度随正、负极输出电压变化规律Fig.3 The voltage unbalance factor varies with the positive and negative output voltage

2 基于分布式协同的不平衡电压控制

2.1 电压下垂控制

在双极直流微电网中，为了降低因功率不平衡而造成的母线电压偏差，本文采用一次控制和二次控制相结合的分布式协同控制。完整的分布式协同控制方案如图4所示。一次控制采用电压下垂控制，主要调节直流变换器的输出电压[28]；二次控制则进一步调整一次控制产生的电压、功率偏差。图4中i表示双极直流微电网中的第i个分布式电源，j、k表示与i节点有通信联络的相邻分布式电源，下标p、n分别表示正、负极。

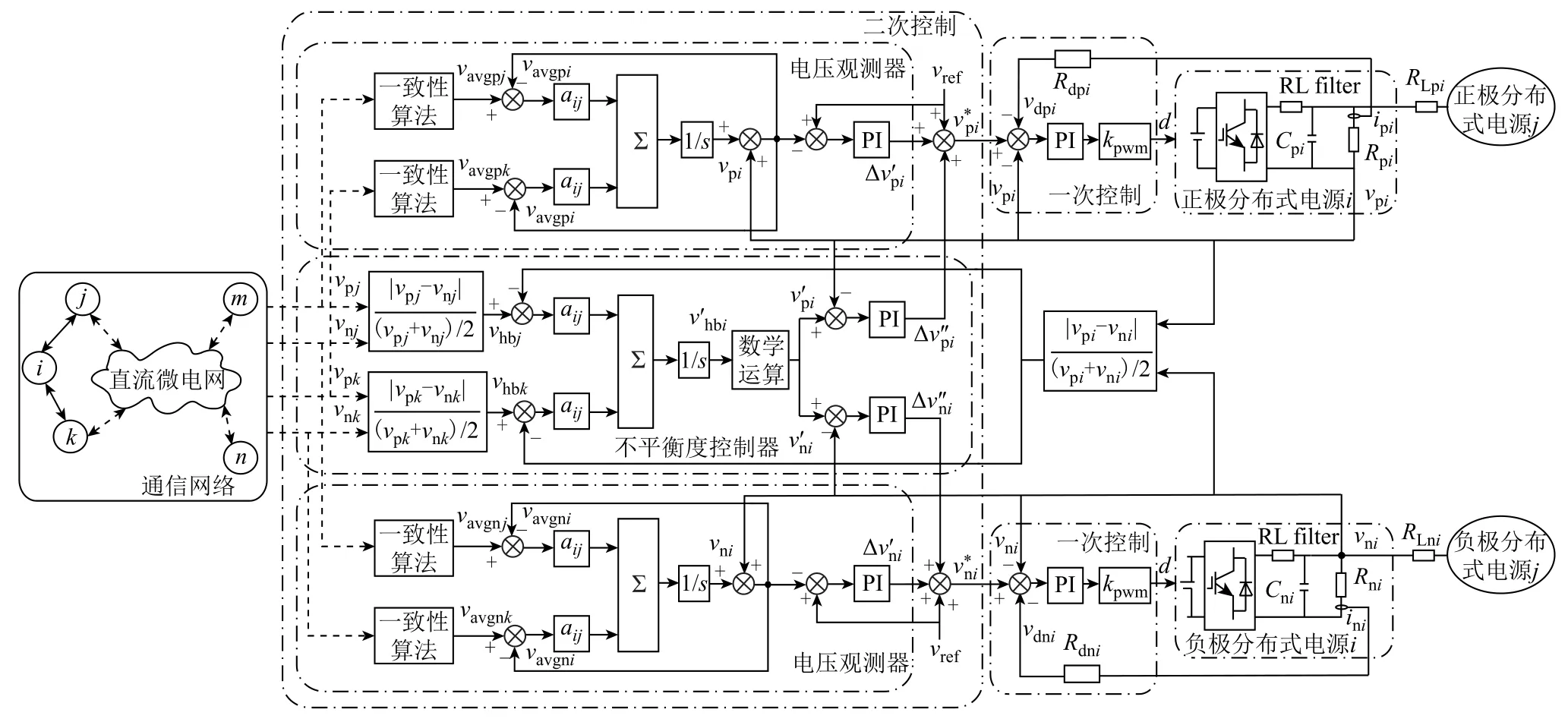
图4 完整分布式协同控制方案Fig.4 The complete distributed cooperative control scheme

在控制方案中，采用下垂控制作为一次控制，实现多个变换器并联运行时负荷功率的自动分配，维持系统稳定运行。一次控制包括电压下垂控制器和虚拟阻抗环，虚拟阻抗环按式（4）设计。

式中，Rdpi、Rdni分别为正、负极虚拟阻抗；ipi、ini分别为正、负极负载电流；vdpi、vdni分别为虚拟阻抗的输出电压，即输出电流的比例部分，能使电压基准值随电流的增加而减小。将虚拟阻抗环的输出电压vdpi和vdni与电压的基准值相减，差值通过PI下垂控制器，生成控制 DC-DC变换器开关的占空比d。一次控制中采用虚拟阻抗实现电压下垂控制，但虚拟阻抗引起的电压下降会产生电压偏差，选用较小的虚拟阻抗电压偏差小，但是易造成微电网的不稳定，因此需合理选择虚拟阻抗的大小。

2.2 不平衡平均电压二次控制

电压下垂控制无法完全消除直流母线电压偏差，而基于平均动态一致性理论的分布式协同控制可根据自身及相邻节点数据信息实现协同控制，其基本原理为

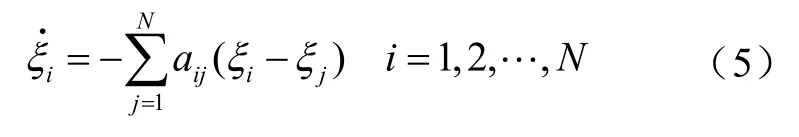
式中，iξ和jξ分别为节点i和节点j的状态变量；aij为节点i和节点j进行信息交换的通信权重。平均一致性算法的通信网络可用图表表示，其图表的拉普拉斯矩阵L=[lij]∈RN×N，满足

二次控制在为一次控制提供参考电压的同时，还需协调电压不平衡度和母线平均电压趋于一致，以减小功率波动较大时电压失衡。由于线路阻抗的存在，不同直流变换器接入点的母线电压不同，为获得直流母线电压的平均值，构建如图4中所示的不平衡电压观测器。对图1所示的双极直流微电网，根据平均一致性算法，第i个直流变换器直流母线平均电压为

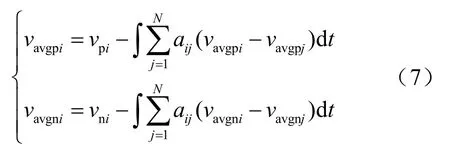
式中，j节点为一致性算法通信网络中与i节点关联的节点；vavgpi、vavgpj和vavgni、vavgnj分别为正、负极第i个和第j个电压观测器输出的母线平均电压。

不平衡电压观测器可结合自身和相邻单元的信息实时更新下一时刻的平均电压输出量，进而有效估计双极直流微电网的母线平均电压。将直流母线额定参考电压vref与母线平均电压vavgpi、vavgni间的误差项通过比例积分控制器处理，生成母线电压的修正项。

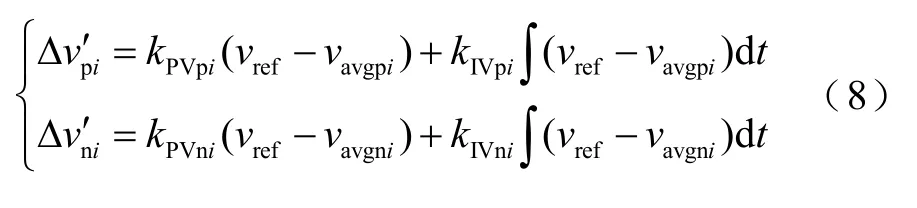
2.3 不平衡度二次控制

为使电网中各节点在运行过程中的电压不平衡度趋于一致，减小电压不平衡度对双极直流微电网稳定运行的影响，设置如图4所示的不平衡度控制器。根据平均一致性算法，可以得到期望的电压不平衡度为

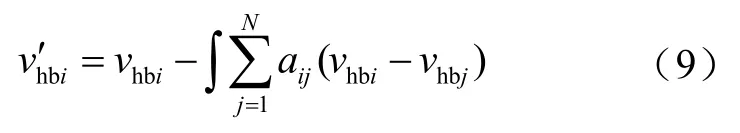
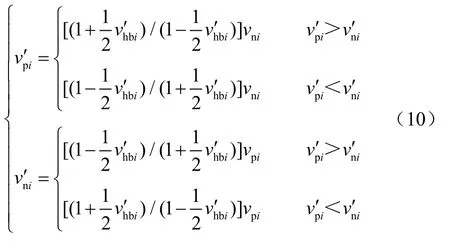
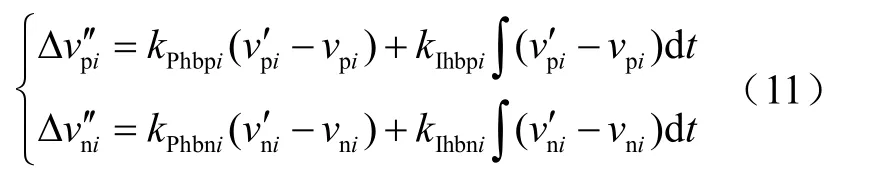
将不平衡电压观测器和不平衡度控制器得到的两个修正项加到母线额定参考电压，可得双极直流微电网电压下垂控制的参考电压为

3 双极直流微电网小信号稳定分析

为研究双极直流微电网系统的小信号稳定性，本文建立控制策略的小信号模型，并通过根轨迹及 Nyquist图分析所提控制策略对系统稳定性的影响。

在双极直流微电网中，分布式电源通过DC-DC变换器接入直流母线，在忽略变换器开关损耗后，其输入输出特性为

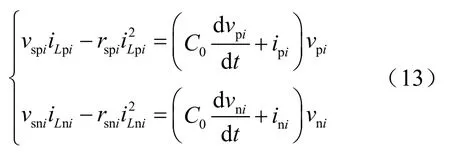
式中，vspi、vsni分别为i节点正、负极电源电压；iLpi、iLpi分别为i节点正、负极电感电流；rspi、rsni分别为i节点正、负极电源内阻；C0为滤波电容。对式（13）进行线性处理可得

式中，vopi、voni分别为系统稳定时的正、负极母线电压；iopi、ioni和iLopi、iLoni分别为系统稳定时的正、负极负载电流和电感电流。

根据式（14）可得控制系统的一次控制动态结构图如图5a所示。该系统以参考电压电流Δipi（或Δini）为输入量，母线电压Δvpi（或Δvni）为输出量，化简框图，再根据欧姆定律可得到以为输入，Δvpi（或 Δvni）为输出的一次控制的传递函数为

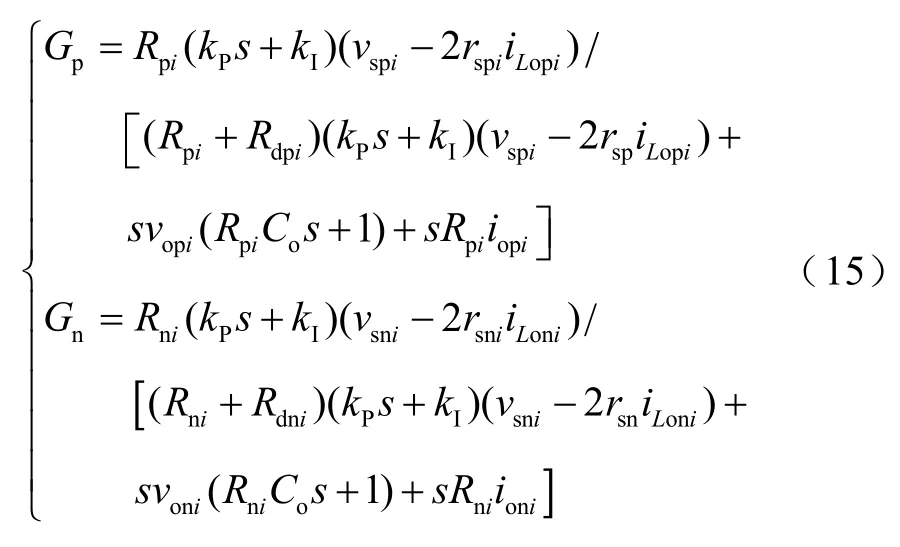
式中，Gp、Gn分别为正、负极一次控制的传递函数；kP和kI分别为一次控制中 PI的比例系数和积分系数；Rpi和Rni分别为i节点正、负极负载。

图5 控制系统框图Fig.5 The structure of control system

由式（8）、式（11）、式（12）和式（16）可知一次控制中的输入量为

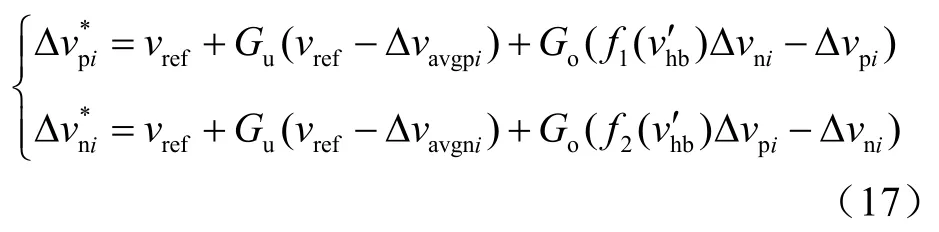
式中，Gu和Go分别为平均电压观测器和不平衡度控制器的PI传递函数，且满足

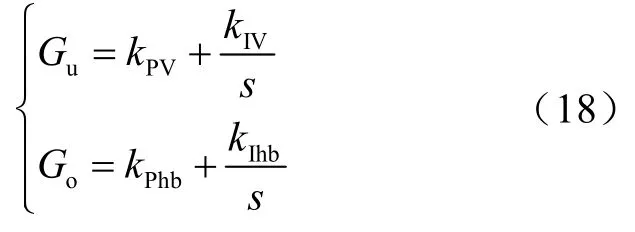
式中，kPV、kIV分别为不平衡电压观测器的比例系数和积分系数；kPhb、kIhb分别为不平衡度控制器的比例系数和积分系数。

联立式（15）、式（17）、式（18）并化简可得双极直流微电网加入二次控制后的系统框图如图5b所示。由系统框图可知，双极直流微电网中正、负极之间存在耦合，结合式（7）中平均母线电压与母线电压的关系，通过化简可得以vref为输入，Δvpi（或Δvni）为输出的系统传递函数，并进行小信号稳定性分析。

依次在二次控制中加入平均电压观测器和不平衡度控制器，得到以vref为输入，Δvpi（或Δvni）的控制系统的根轨迹和Nyquist图如图6和图7所示。由图6可知，其根轨迹系统零极点均位于负半平面，且远离虚轴；由图7所示，不平衡度控制器加入前后系统的Nyquist图不包围（-1，j0）点，系统稳定。

图6 加入平均电压观测器而未加不平衡度控制器时根轨迹Fig.6 Root locus when the average voltage observer is added without the unbalance factor controller

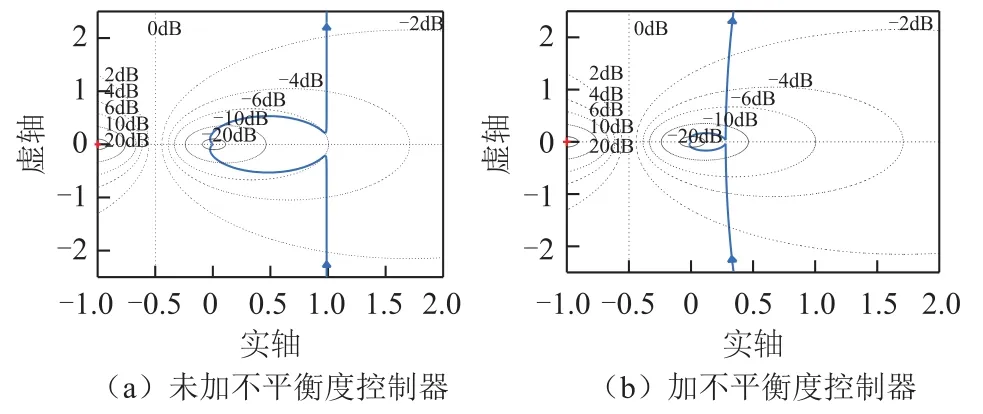
图7 加入平均电压观测器的控制系统Nyquist图Fig.7 The figure of Nyquist with average voltage observer

4 仿真及实验验证

4.1 仿真验证

为验证所提控制策略的有效性，在 Matlab/Simulink中搭建图8所示的仿真模型，其中母线平均电压、不平衡度一致性控制（不平衡度参考值xref为0.5%）的通信拓扑分别如图9a、图9b所示。通信拓扑采用双向环形拓扑，在某一通信链路失效时依然能够保证通信的可靠性[19-20]。

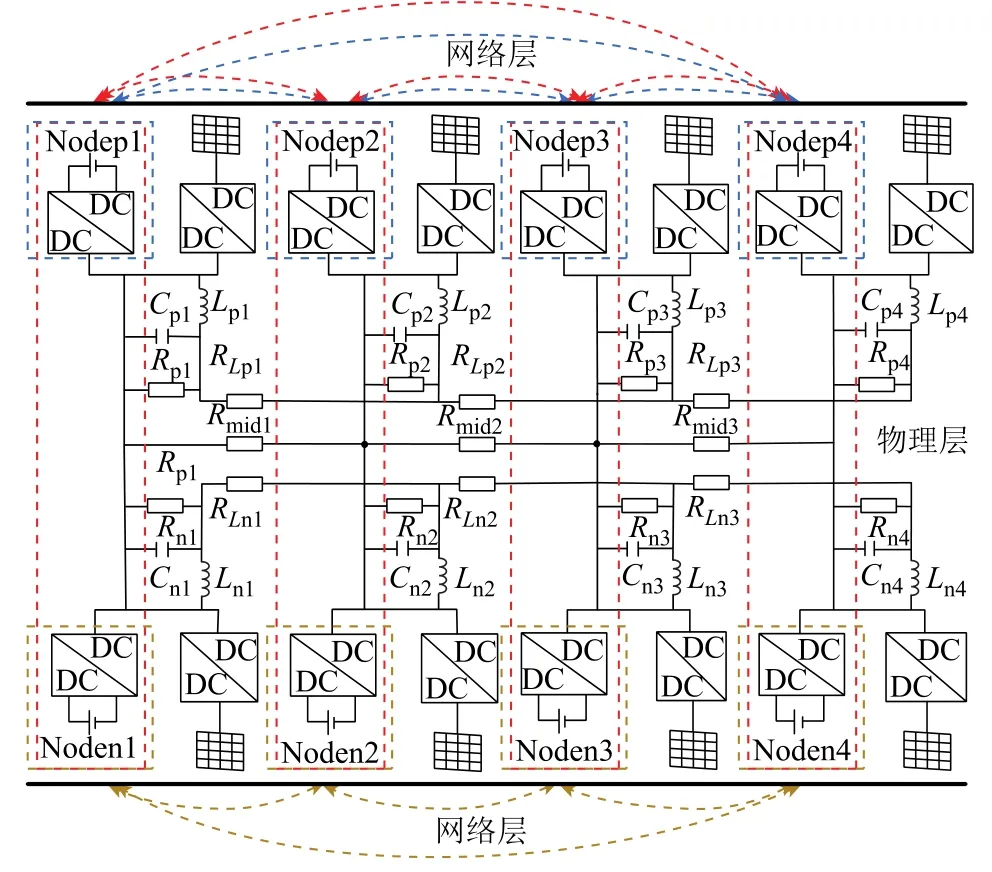
图8 仿真结构示意图Fig.8 The schematic diagram of simulation structure

图9 通信拓扑结构Fig.9 Communication topology

在平均电压一致性控制设计中，采用 0-1权重的邻接矩阵为

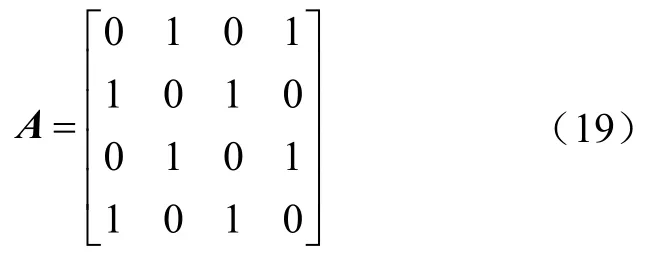
由于不平衡度一致性控制中增加了电压不平衡度参考值，其0-1权重的邻接矩阵为

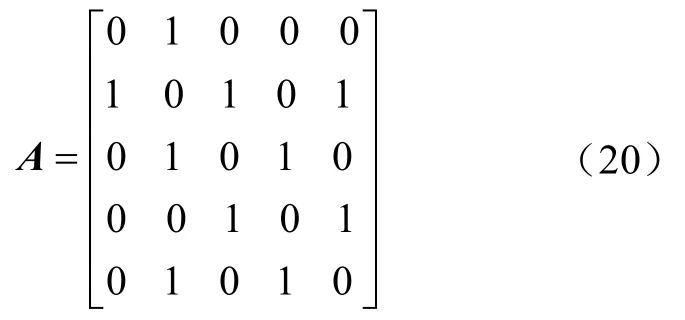
初始时刻，正极各节点的负载分别为Rp1=10Ω、Rp2=20Ω、Rp3=20Ω、Rp4=20Ω，负极各节点的负载分别为Rn1=20Ω、Rn2=40Ω、Rn3=20Ω、Rn4=5Ω，仿真模型和控制器的相关参数见表1。

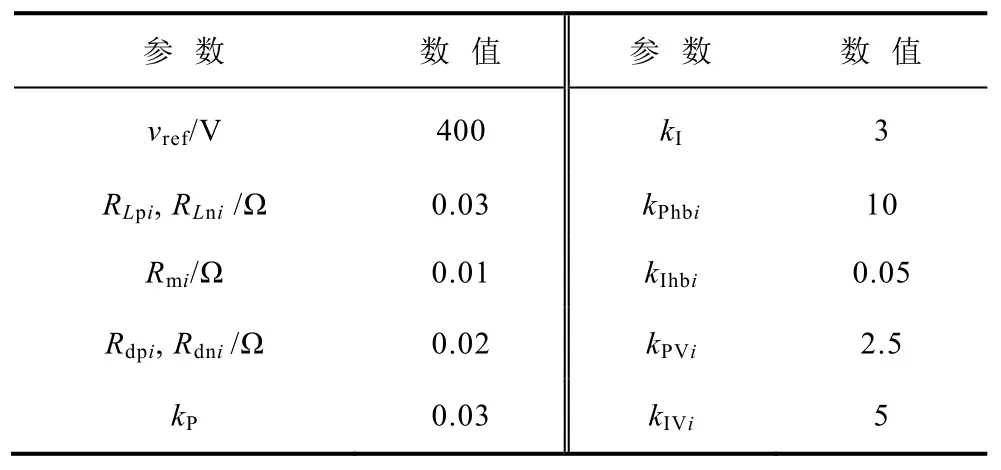
表1 系统参数Tab.1 The system parameters

算例1：本文所提出的基于一致性算法的二次控制本质上是对下垂控制的改进，通过动态平均电压和不平衡度一致性算法，用以补偿下垂控制的初始参考电压，并通过相邻节点间的通信达到双极直流微电网平均电压和不平衡度的一致。在下垂控制的改进方法中，有通过算术平均法求取系统状态量均值，再利用偏差信号进行调节的输出补偿。文献[29]基于算术平均法动态调节下垂控制参考电压，实现了直流微电网中分布式储能单元SOC均衡以及负荷功率的动态分配。为验证本文控制方案的有效性，系统采用电压下垂控制作为一次控制，首先在二次控制中仅投入本文不平衡电压观测器，不平衡度控制器未投入；然后采用文献[29]中的控制算法作为二次控制投入；最后在双极直流微电网中投入本文所提出的完整二次控制策略，即同时投入不平衡电压观测器和不平衡度控制器。各仿真结果如图 10所示。

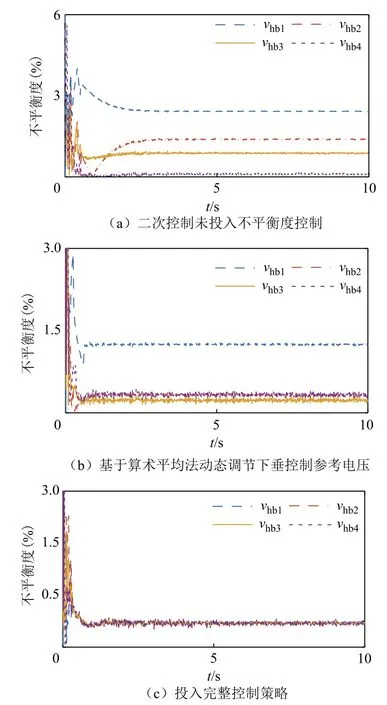
图10 不同控制下系统电压不平衡度Fig.10 The voltage unbalance factor of system under different control

由图10a可知，由于二次控制中仅投入电压观测器，没有电压不平衡度控制器，各正、负极节点的不平衡度不收敛，且节点1的电压不平衡度远大于其他节点，甚至接近不平衡度的限制 3%。由图10b可知，采用基于算术平均法动态调节下垂控制的参考电压，各正、负极节点的不平衡度得到调节，各节点间不平衡度在限定范围内差值减小，但仍存在偏差且不趋于一致。由图10c可知，本文控制策略完全投入后，在电压不平衡度控制器作用下，各正、负极节点的不平衡度趋于一致，且能收敛于参考值0.5%，与图10a与图10b相比，极间电压不平衡明显得到改善。

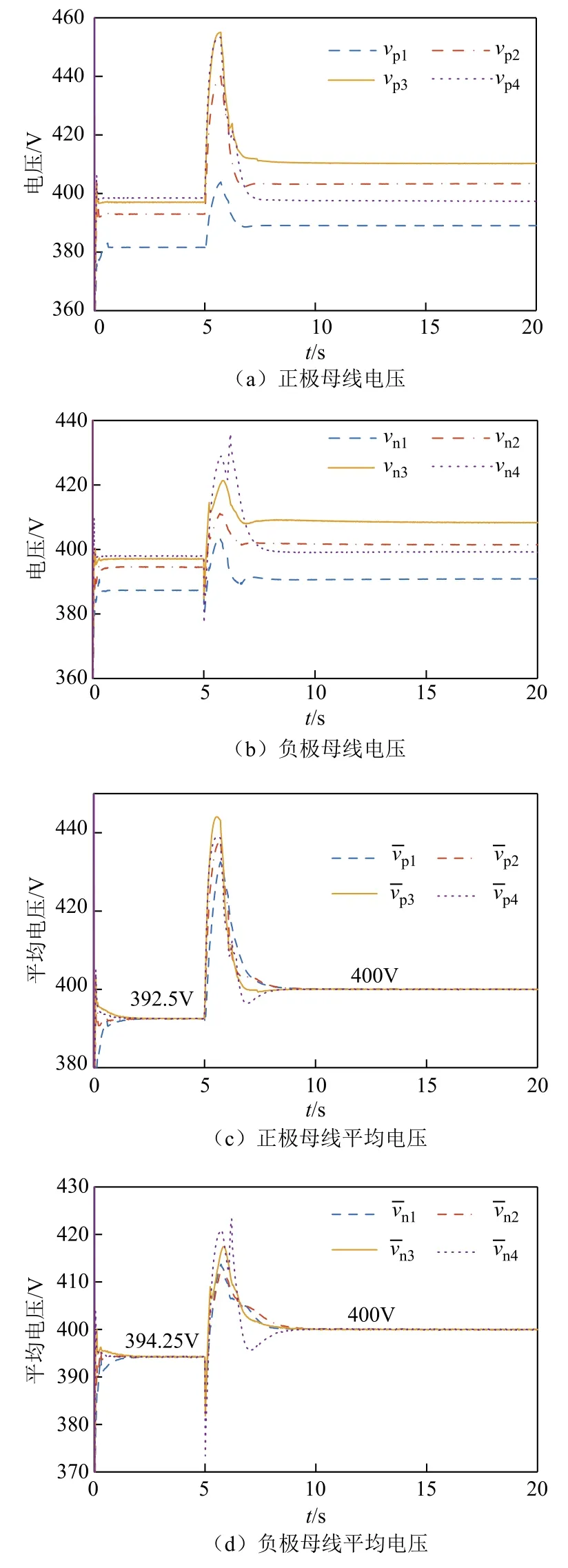
图11 二次控制投入系统电压响应Fig.11 The voltage response of the system with secondary control input

算例2：0～5s，系统仅采用电压下垂一次控制；5～20s时，投入本文所提出的完整二次控制。在上述模型参数的设置下，仿真结果如图11所示。由图11可知，0～5s，由于存在直流线路阻抗，正、负极直流母线电压均偏离额定值400V，此外，正极母线平均电压为 392.5V，负极母线平均电压为 394.25V。由图11a和图11b可知，在5s投入二次控制后，正、负极母线电压均上升，但由于线路阻抗的存在，正、负极母线电压与额定值不同，但均接近于额定值400V。由图11c和图11d可知，在二次控制投入后，由于各母线电压的抬升，正、负极母线平均电压可以稳定在额定值400V，平均电压偏差减小到0。

算例3：6s时将负载A(160kW)并联投入正极第4个节点，13s时将负载B(32kW)并联投入到负极第2节点，仿真结果如图12所示。由图12a可知，负载变化时，不平衡电压观测器输出的母线平均电压均会收敛于额定值。由图12b可知，不平衡度控制器能够在正、负极负载发生变化时快速响应，将网络中各节点的不平衡度收敛于同一值，即参考值0.5%，实现正、负极直流母线电压的平衡。

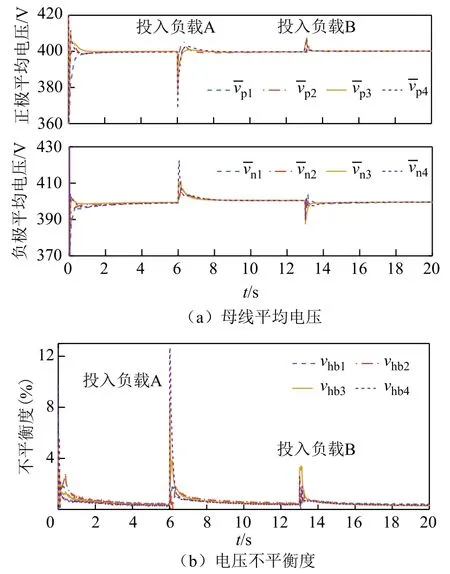
图12 负载变化系统响应Fig.12 System response to load changes

算例4：一致性算法中，通信权重aij不仅能有效反映双极直流微电网中的节点信息，还会影响系统状态变量一致性的收敛速度。为验证通信权重aij对电压不平衡控制的影响，在其余系统参数均相同的条件下，改变通信权重aij值，得到其与系统相应调节时间的关系如图13所示。由图13可知，通信权重aij越大，系统调节时间越短，收敛速度越快。取通信权重aij值分别为2和10，并且5s时在正极第4个节点并联增加32kW的负载。此时系统电压不平衡度曲线和正极母线平均电压如图14所示。由图14a和图14b可知，当负载发生变化时，aij=10时电压不平衡度曲线和母线平均电压的收敛速度更快，更容易趋于一致。

图13 通信权重与调节时间关系Fig.13 The relationship between communication weight and adjustment time

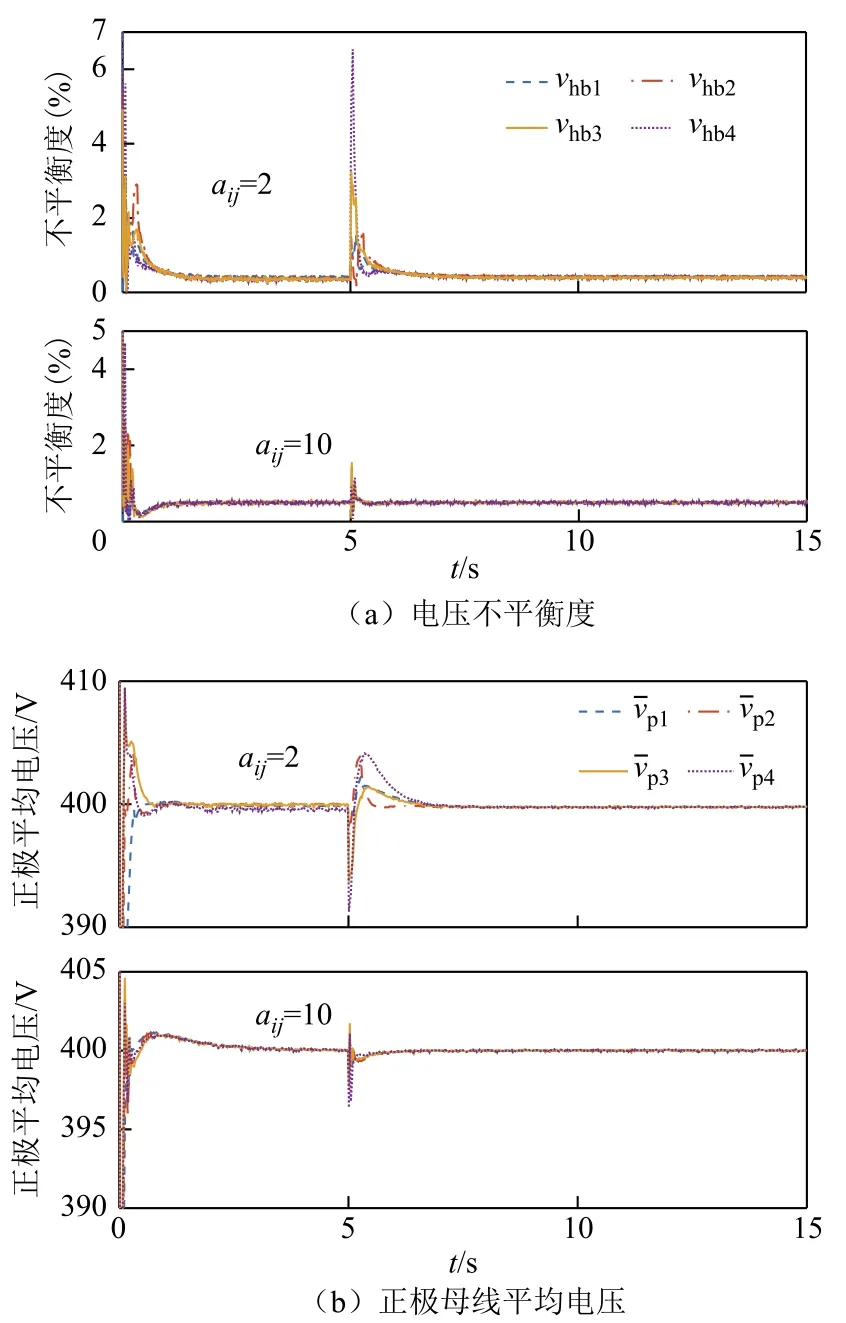
图14 通信网络变化系统响应Fig.14 The system response to changes in communication networks

4.2 实验验证

本实验搭建如图 15所示的实验平台来验证所提出的双极直流微电网不平衡电压控制策略的正确性和有效性。实验平台由8个直流源（正、负极各4个）、DC-DC变换器、通信模块、电阻负载等组成，实验中直流源设置为 24V，线阻为 1Ω，负载为 20Ω左右不均，母线电压额定参考电压设置为12V。

图15 实验平台Fig.15 The experiment platform

实验初始时刻，正、负极直流电源变换器仅由一次下垂控制控制，在t1时刻启动二次控制，正、负极直流母线电压波形如图16a所示。初始时刻，正、负极各4个节点的母线电压均存在电压偏差，平均电压估计低于12V。启动二次控制后，尽管正、负极直流母线电压没有保持在12V，但是母线电压均有所抬升，母线平均电压也会有所提高，并可以保持在额定值12V。通过实验中直流电压数据计算得到电压不平衡度如图16b所示。由图16b可知，在一致性控制作用下，双极直流微电网中各节点的电压不平衡度明显降低，且均稳定在1.3%左右，基本达到一致。