基于自适应变分模式分解的非稳态电压闪变包络参数检测

张民谣 高云鹏 吴 聪 黄 瑞,2 曹一家

（1. 湖南大学电气与信息工程学院 长沙 410082 2. 国网湖南省电力有限公司 长沙 410004）

0 引言

电力系统中的电压波动与闪变通常是由冲击性功率负荷（如轧机、电弧炉）引起的，给工业生产和社会生活带来严重影响[1-2]。针对电压闪变准确检测已开展大量研究，传统的平方检波法、有效值检测法和整流检测法在稳态下检测均具有较高的准确性[3]。

当前智能电网建设中大量电力电子设备的应用，越来越多的非线性和冲击性负荷接入，导致电网产生大量非稳态时变闪变信号[4]。针对非稳态电压闪变包络参数检测与分析，近年来新的方法被逐渐应用于其中，快速傅里叶变换（Fast Fourier Transform,FFT）作为包络参数检测中广泛应用的谱分析方法[5]，有研究人员采用各种加窗插值算法提高FFT的计算准确度，克服非同步采样时存在的频谱泄露和栅栏效应[6]，但其要求被分析的信号波形须是稳态的，且变换对整个时间段积分，不具有信号时域信息[7-8]。为了解决上述问题，短时傅里叶变换[9]、S变换[10-11]和小波变换[12]等时频分析方法被用于非稳态时变信号分析。但短时傅里叶变换的时频窗口固定，对于突变过程和多尺度过程效果较差；S变换计算量大、运行时间长；小波变换则存在小波基选择困难的问题。

希尔伯特-黄变换（Hilbert-Huang Transform,HHT）自提出以来被广泛用于各种非平稳信号的分析处理中，同时在时域和频域均具有较高的检测准确度，且有效避免了小波基选取的难题[13-14]，但HHT中的重要组成部分经验模态分解（Empirical Mode Decomposition, EMD）易出现模式混淆问题，有时无法准确分解出所有的闪变包络分量[15]。为了有效解决 EMD中存在的模式混淆问题，变分模态分解（Variational Mode Decomposition, VMD）通过预先设置模式数实现多分量信号的准确分离[16-17]，相比EMD，分解精度更高且可避免模式混淆问题[18-19]，现被广泛应用于机械故障诊断中[20-21]。VMD算法中的模态分解个数K要求在对信号进行分解前就提前设定，但受实际情况的限制，K值通常难以准确设定，如果设置偏大或偏小都会严重影响信号的检测精度[16]。

因此，本文针对非稳态电压闪变包络参数的准确检测，首先通过Hilbert变换检波法提取闪变包络，然后采用损失系数和能量差确定模态分解个数，通过自适应 VMD对闪变包络进行分析，实现闪变包络信号的准确分解，最后通过Hilbert谱分析求取各分量的瞬时频率和瞬时幅值，据此建立基于自适应 VMD的非稳态电压闪变包络参数检测方法，并基于PXI与LabVIEW平台开发闪变参数检测系统，通过仿真和实验实测对本文方法的准确性进行分析与验证。

1 自适应变分模态分解

1.1 变分模态分解

VMD作为一种较新的多分量信号自适应分解方法，旨在将原始信号f分解成K个模态函数uk(t)，并在各模态函数之和与信号f相等的要求下，使每个模态函数的估计带宽之和最小，上述约束变分问题可表述为

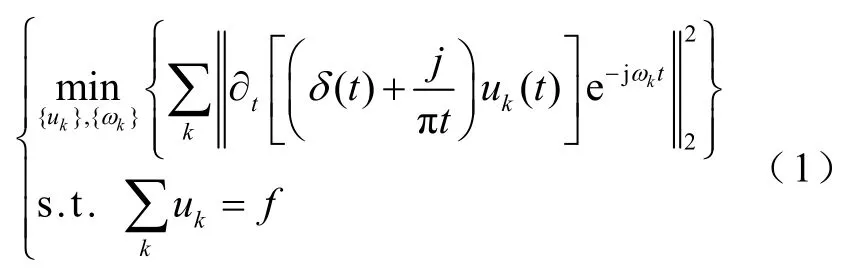
式中，{uk}为各模态分量的集合；{ωk}为各模态对应的中心频率集合；∂t表示对t求偏导；∂(t)为狄拉克函数。

引入 Lagrange乘子λ和二次惩罚因子α使式（1）转化成非约束性的变分问题，其表达式为

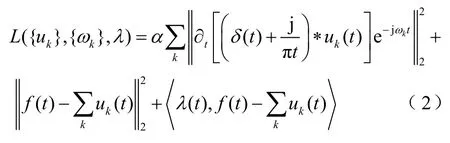
利用 Parseval/Plancherel傅里叶等距变换将式（3）转变到频域，可得二次优化结果为

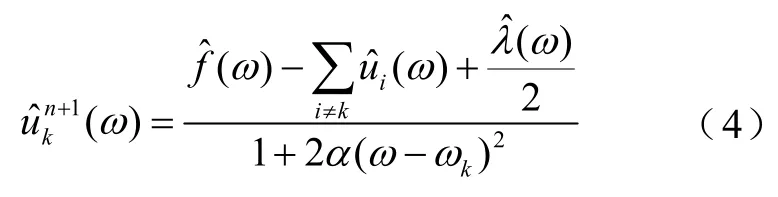
同样将中心频率的取值问题转换到频域，可得中心频率的计算式为

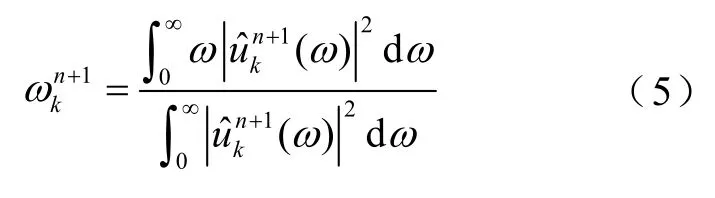
VMD的具体实现过程如下：

（2）令n=n+1，执行整个循环。

（3）取k=1:K，根据式（4）和式（5）更新uk和ωk。

（4）根据式（6）更新λ，有

（5）给定值大于零的判别精度ε，当收敛满足

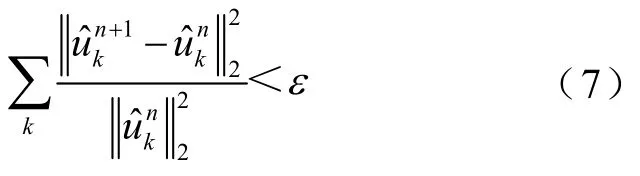
即可停止循环输出结果，否则重新回到步骤（2）。

1.2 VMD的K值自适应确定

由 VMD算法原理可知，其处理信号时需要预先设定模态分解个数K，但受实际情况的限制，K值通常难以准确设定。若K设置偏小会造成某个模态中含有多个分量，致使信息无法完整获取；若K设置偏大会使模态中心频率发生重叠，导致虚假分量出现。为了解决该问题，考虑到范数可用于度量信号能量，采用损失系数e作为指标，即分解残差能量与原始信号能量之比，其表达式为

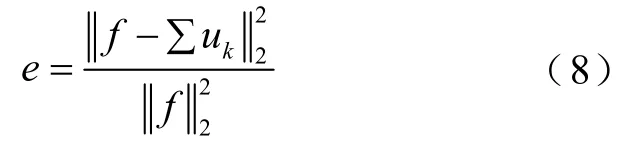
式中，uk为第k个模态函数，∑uk为重建信号。损失系数e的阈值表示为μ1，经过大量计算，本文中阈值μ1设定为 0.01。

仅由损失系数e确定的K值会偏大，因此，本文进一步引入能量差方法，此处能量含义为数字信号转换到频域后各点信号幅值二次方后求和。首先根据损失系数e设置最大分解个数Kmax，计算原始信号的能量值E，逐步求取模态分解个数设定为k时的累加能量Ek（k=1, 2, …,Kmax），然后将E和Ek作差取绝对值得到能量差值，当两个信号在相同采样率与采样时间情况下的频域能量相差越小，说明两个信号越相似，因此，选取能量差最小的k值作为模态分解个数K。当能量差值相同时，选取较小的k值为最佳模态分解个数。

本文提出的自适应变分模态分解（Adaptive Variational Mode Decomposition, AVMD）具体实现步骤如下：

（1）初始化K为1。

（2）令K=K+1，进行VMD分解。

（3）计算损失系数e。

（4）重复步骤（2）和步骤（3）直至损失系数e小于设定的阀值μ1，得到Kmax。

（5）将最大模态分解个数设为Kmax，先求取原始信号的能量值E，然后计算当模态分解个数设为k时的累加能量Ek（k=1, 2, …,Kmax），并求取能量差值，选取能量差最小时的k值作为最佳模态分解个数K，再次执行 VMD，即可得到K个有限带宽的模态分量ui(t)。

2 基于AVMD的非稳态闪变包络检测

2.1 电压闪变包络提取

闪变是指人眼对灯光光照强度受电压波动影响发生变化时的反应，可视为是波动电压对工频载波电压的调制结果[22-23]，其电压瞬时值的解析式为

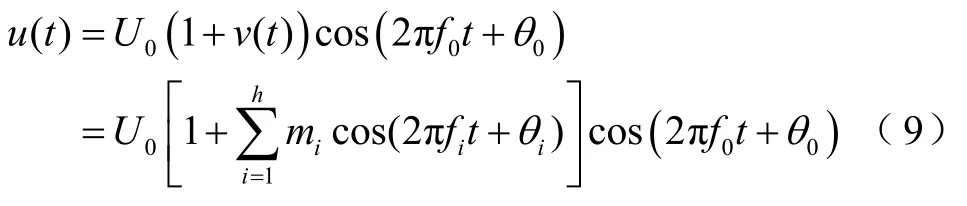
式中，U0、f0和θ0分别为工频载波电压的幅值、频率和初相位；mi、fi和θi分别为闪变包络信号的波动系数、频率和初相位。电压闪变包络参数检测的关键在于提取出闪变包络系数mi和频率fi。

Hilbert变换是常用的闪变包络提取方法[24]，设任意连续时间信号x(t)，Hilbert变换定义为

式中，h(t)=1/(πt)。

对式（9）所示的电压闪变信号u(t)进行Hilbert变换，得到其共轭信号uˆ(t)，令

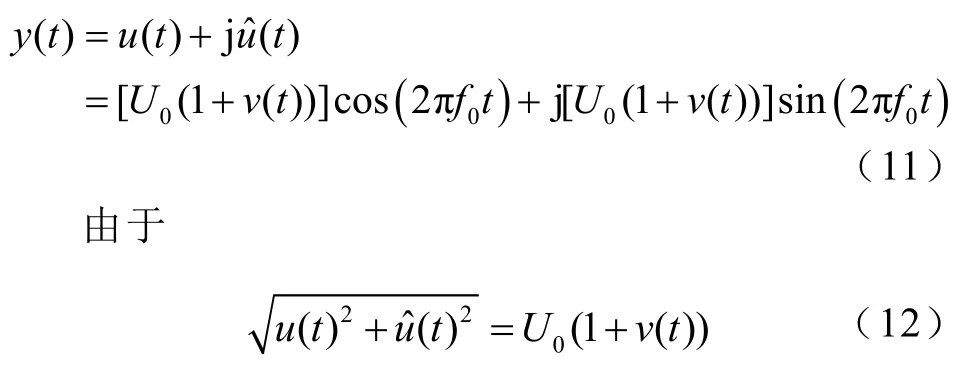
故对y(t)取模后，滤除直流分量，即可得到电压闪变包络信号为

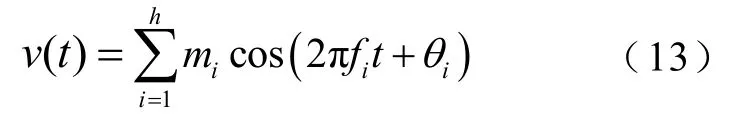
2.2 非稳态闪变包络的AVMD处理

利用本文提出的 AVMD算法对提取出来的闪变包络信号v(t)进行分解可以得到各个闪变包络分量ui(t)，即

对第i个闪变包络分量ui(t)进行 Hilbert变换，得到其共轭信号则第i个闪变包络分量ui(t)的瞬时幅值为

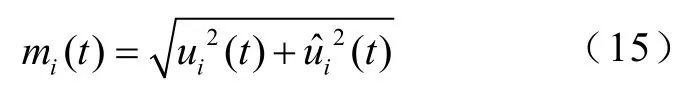
φi(t)为第i个闪变包络分量ui(t)的相位函数，有

对式（16）求导可得第i个闪变包络分量ui(t)的瞬时频率fi(t)为

3 仿真实验与分析

3.1 单一频率非稳态包络调制

为了进一步证明本文提出方法的有效性，首先基于 Matlab对单一频率非稳态包络调制下的电压闪变信号进行仿真分析。考虑到作用最显著的是8.8Hz调幅波的正弦波波动电压，本文以该频率闪变包络信号为例进行仿真，设工频载波电压的幅值U0为 1(pu)，工频f0为 50Hz，闪变包络系数mi为2.5×10-3(pu)，仿真时闪变起止时刻分别设定为2.0s和8.0s，仿真结果如图1所示。

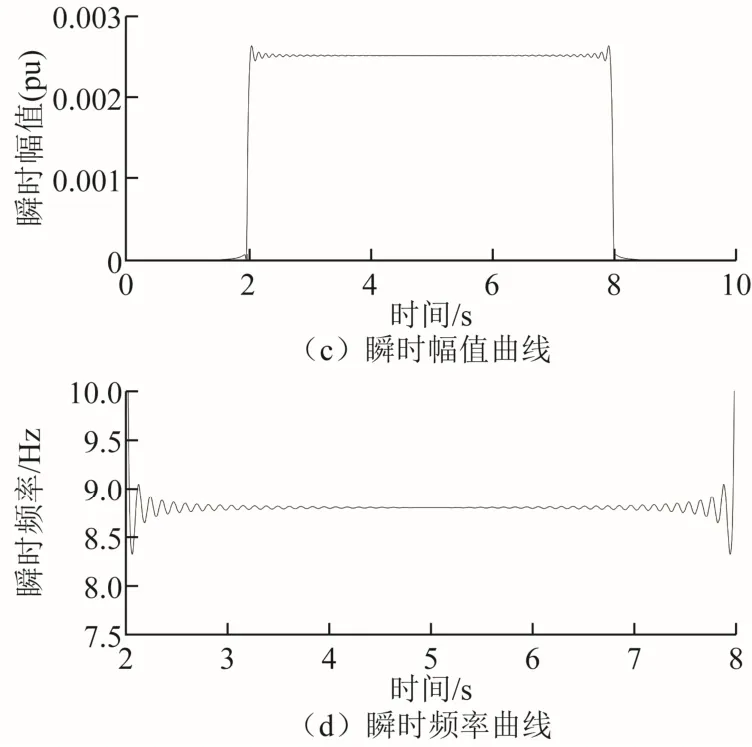
图1 单一频率非稳态包络调制的测量结果Fig.1 Measurement results of single frequency nonstationary envelope component

由图1c和图1d分别可见，非稳态闪变包络信号在2s开始并在8s结束，闪变包络频率fi为8.8Hz，系数mi为 2.5×10-3(pu)，证明本文提出方法在单一频率非稳态包络调制的情况下不仅能准确测量出闪变参数，并可得到闪变信号的时域信息。

选取IEC标准给出视感度S(t)=1觉察单位的电压波动参数进行仿真（未考虑闪变发生的起止时刻），得到闪变参数测量的相对误差见表1。

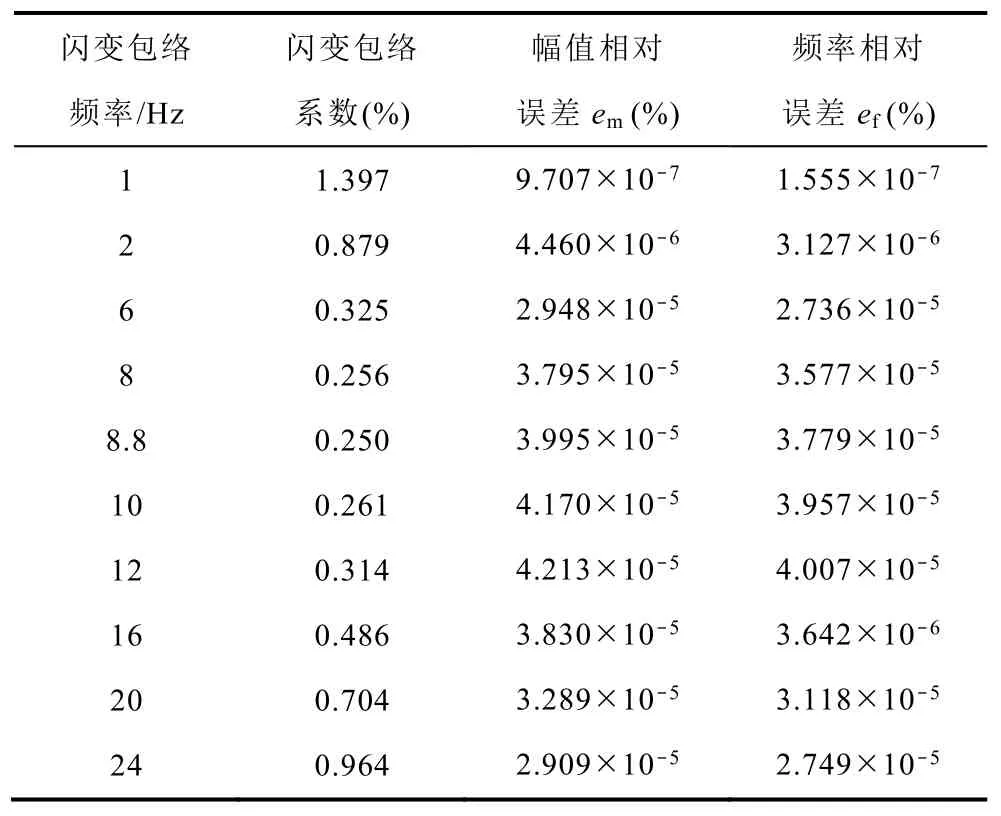
表1 单一频率稳态包络调制的测量结果Tab.1 Measurement results of single frequency stationary envelope modulation

由表1可知，当闪变包络信号中仅含有单一频率调制分量时，闪变包络系数和频率的相对误差均在10-4%以内，满足IEC标准的误差要求。

3.2 幅值时变包络调制

对式（9）所示的电压闪变信号，设工频载波电压的幅值U0为1(pu)，工频f0为50Hz，闪变包络频率fi为17Hz，闪变包络系数mi为

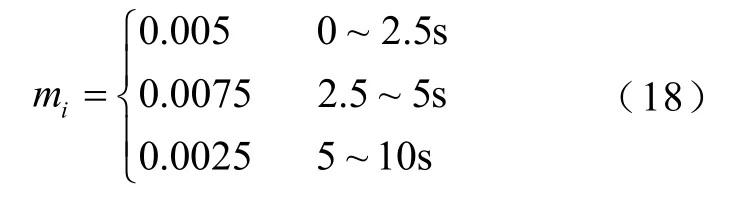
仿真结果如图2所示，由图2c和图2d分别可见，闪变包络系数mi在 2.5s和 5.0s时发生变化，闪变包络频率为 17Hz，因此，采用本文提出的基于自适应VMD的非稳态电压闪变包络参数检测方法可有效实现包络幅值发生变化的闪变信号的准确检测。

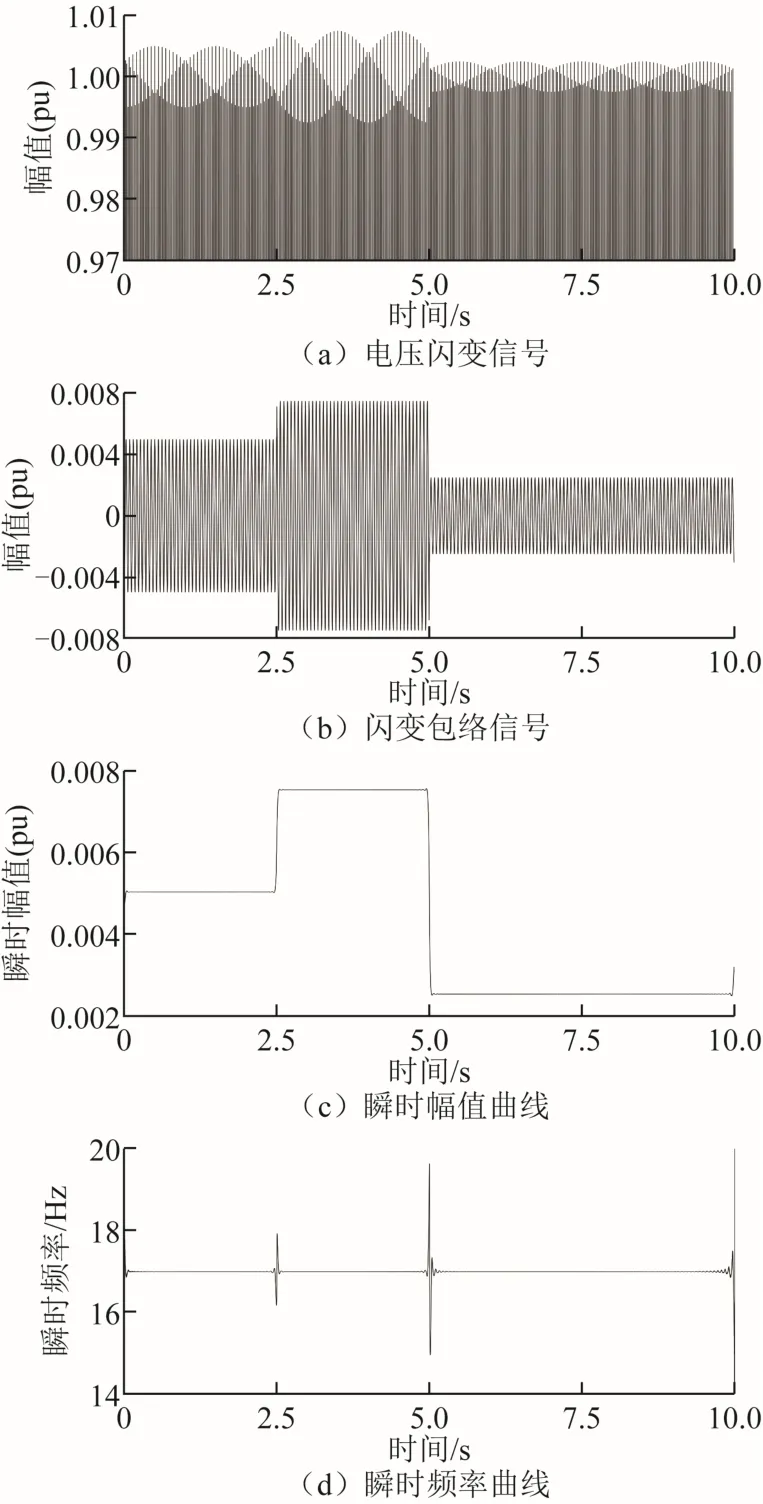
图2 幅值时变包络调制的测量结果Fig.2 Measurement results of amplitude-varying envelope modulation

3.3 多频率非稳态包络调制

复杂电网环境中，闪变包络信号中可能同时存在多个频率分量，为了证明本文提出方法在多频率非稳态包络调制情况下的有效性，设置闪变包络信号中包含三个波动分量，其测量结果见表2，其中，频率为 25Hz的波动分量发生的起止时刻分别设定为2.0s和6.0s，多频率非稳态包络调制的测量结果如图3所示。

表2 多频率非稳态包络调制的测量结果Tab.2 Measurement results of multiple frequency nonstationary envelope modulation

由图3a可见，损失系数和能量差值确定的模态分解个数K值为3，与闪变包络信号实际包含频率分量个数相同，实现了 VMD算法的模态分解个数自适应确定。由表2和图3可知，对多频率非稳态包络调制下的电压闪变信号进行检测时，基于本文方法得到的误差结果仍满足IEC标准要求，可见本文提出方法在多频率非稳态包络调制的情况下仍具有较高的准确性。

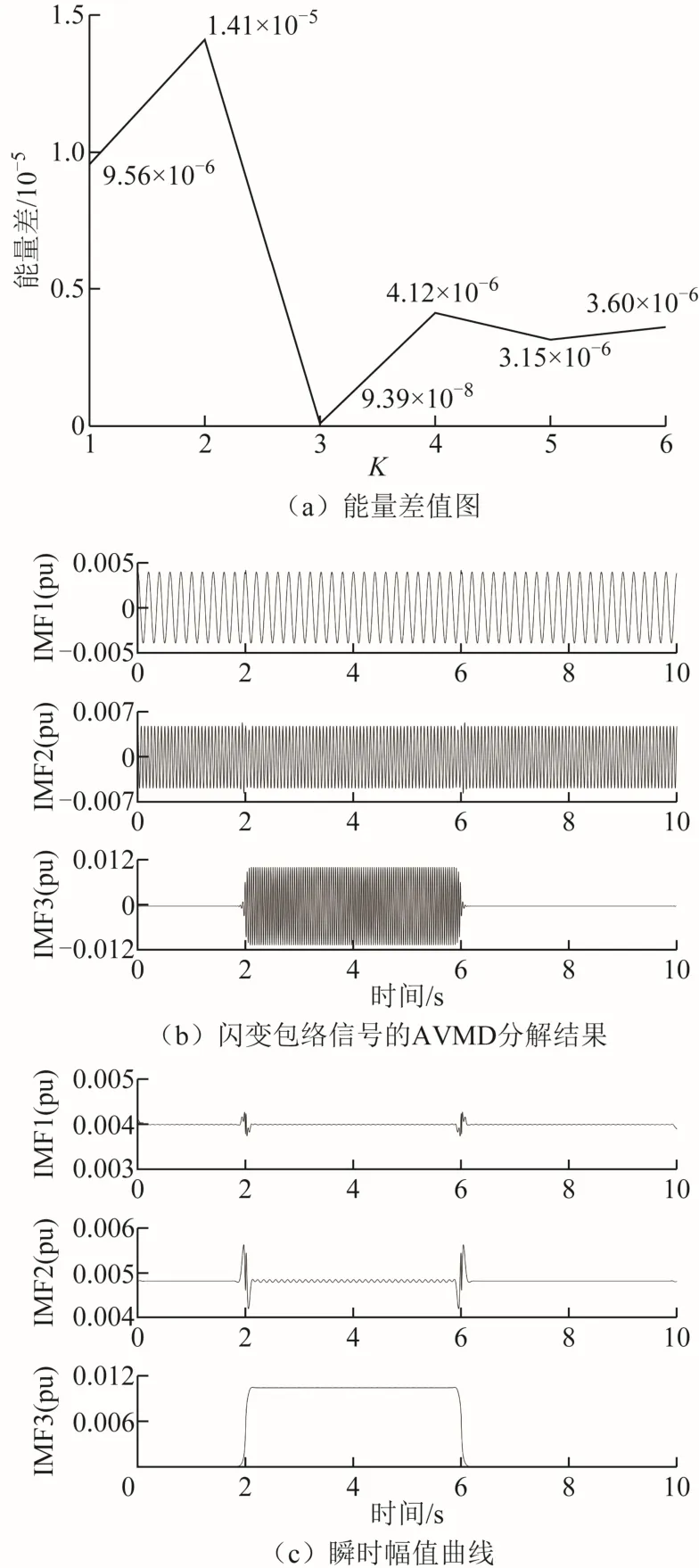
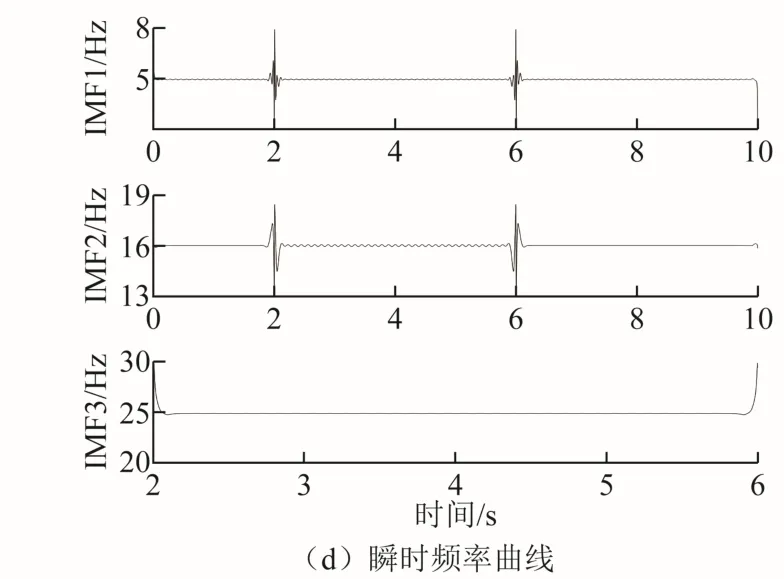
图3 多频率非稳态包络调制的测量结果Fig.3 Measurement results of multiple frequency nonstationary envelope modulation

将AVMD与HHT中的EMD算法进行比较，对表2所示的闪变包络信号进行EMD处理，仿真结果如图4所示。由图4可见，EMD存在明显的模式混淆问题，无法准确分解出所有包络分量，而本文提出方法可有效避免模式混淆问题。

图4 闪变包络信号的EMD分解结果Fig.4 Decomposition results of flicker envelope signal with EMD method

3.4 叠加谐波影响

供用电系统中的各种波动性负荷在引起电压波动时，也会产生各类谐波分量。为了证明在含有各类谐波的情况下，本文提出方法检测电压闪变包络参数的准确性，对含有各类谐波的电压闪变信号进行分析。设工频载波电压的幅值U0为1(pu)，工频f0为50Hz，闪变包络系数mi为0.1(pu)，闪变包络频率fi为 8.8Hz，仿真得到闪变参数测量的相对误差见表3。

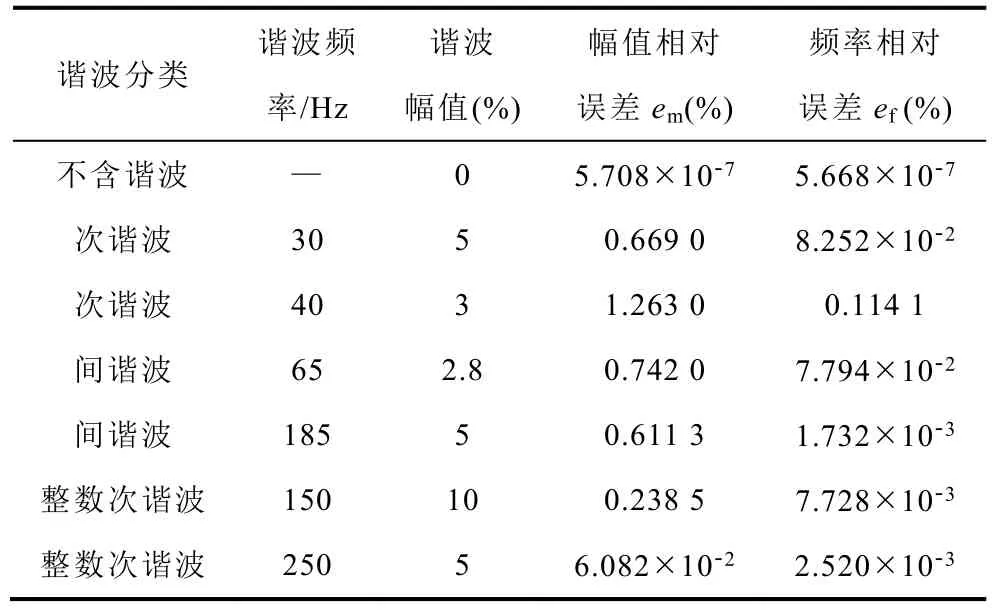
表3 谐波干扰的测量结果Tab.3 Measurement results under the harmonics interference

由表3可知，当闪变信号叠加不同频率的谐波分量时，闪变参数测量的相对误差约在1%以内，因此，本文方法在各类谐波干扰存在时仍可有效实现闪变参数的准确测量。

3.5 电网工频偏移影响

在当前复杂电网环境下，电网工频容易受到各种因素的影响而出现轻微波动，导致信号间互相干扰而降低测量结果的准确度。为了证明本文提出方法在电网工频出现波动时的准确性，仿真设闪变包络频率fi的变化范围为 0.5～35Hz，工频f0在49.5～50.5Hz的频率范围内变化，其他参数设置和3.4节相同，测量结果如图5所示。

图5 电网工频波动时的测量结果Fig.5 Measurement results under power grid frequency fluctuation

由图5可见，当电网工频发生波动时，闪变参数测量的相对误差均在0.1%以内，因此，本文方法在电网工频发生波动的情况下仍可有效实现闪变参数的准确测量。

3.6 添加噪声干扰影响

由于外界环境、设备误差和人员操作等影响，采样信号中常含有噪声，噪声干扰会降低测量结果的准确性。为了检验本文提出方法在含噪声情况下的准确性，仿真设置闪变包络频率fi的变化范围为0.5～35Hz，添加的白噪声信噪比SNR从20～120dB之间变化，其他参数设置和 3.4节相同，测量结果如图6所示。

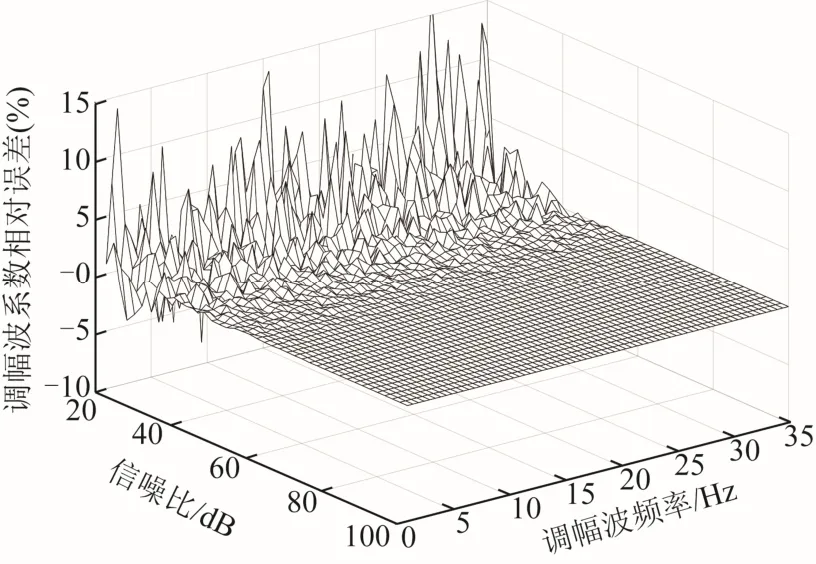
图6 噪声干扰的测量结果Fig.6 Measurement results with noises interference

由图6可见，当系统的白噪声信噪比低于35dB时，闪变参数测量的准确度较低，相对误差在15%以内，当信噪比高于 35dB时，测量相对误差低于5%。考虑到真实电网中的噪声情况，本文提出方法在含有噪声的情况下依旧具有较高的测量精度。

3.7 与现有方法比较

本文选取Nuttall窗双谱线插值FFT方法、HHT方法和本文提出的 AVMD算法对非稳态电压闪变信号进行检测，仿真分析时三种方法输入的信号参数相同，闪变起止时刻随机产生，测量结果见表4。

由表4可知，基于本文提出方法得到的幅值相对误差整体小于 Nuttall窗双谱线插值 FFT方法和HHT方法。由此可知，本文提出的基于 AVMD的非稳态电压闪变包络参数检测方法准确度更高，并且可得到闪变信号的时域信息。

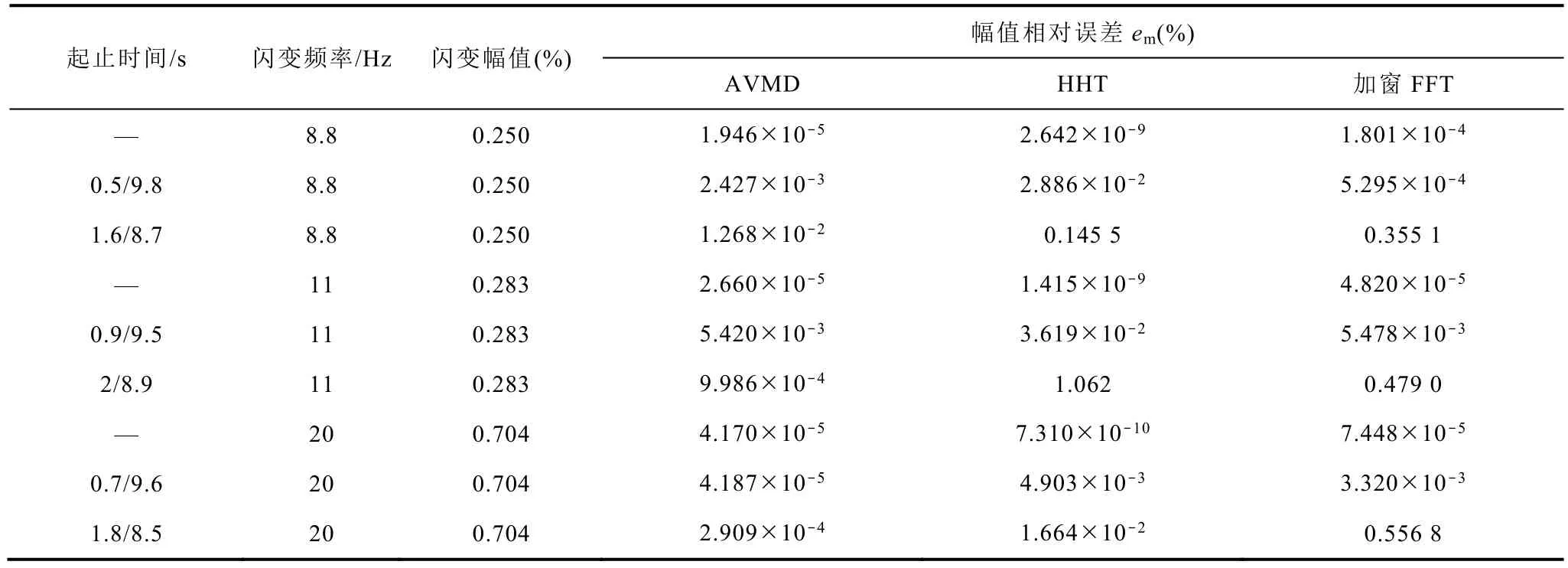
表4 闪变参数测量结果比较Tab.4 Comparison of flicker parameter measurement results

4 实验验证

为了验证本文提出的基于自适应 VMD的非稳态电压闪变包络参数检测方法的有效性，开发基于PXI与LabVIEW的电压闪变参数检测实验平台，并将本文提出方法在上位机LabVIEW软件编程实现，实验平台的系统结构框图和实物图分别如图7和图8所示。

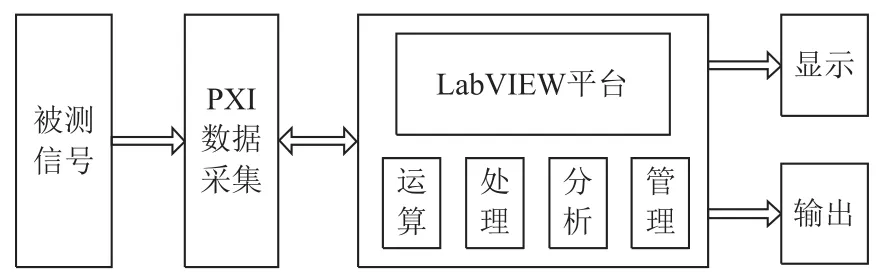
图7 实验平台系统结构框图Fig.7 Diagram of the test platform

图8 实验平台的实物图Fig.8 The physical map of the test platform

信号参数根据式（9）所示的数学模型来设定，由Matlab软件生成TXT格式文件，通过USB闪存盘导入到Agilent 33500B系列波形发生器中产生模拟电压信号，并经由示波器监测显示生成的电压波形，PXI平台由PXIe-1071机箱、PXIe-8840 PXI控制器和NI PXIe-6341数据采集卡组成，信号经数据采集卡采集并传输至上位机中，通过上位机中的LabVIEW软件对本文提出算法进行编程，实现闪变参数检测和分析、电压波形等实时显示以及实验分析结果保存等功能。实验随机选取IEC标准中给出S(t)=1时的闪变频率和闪变幅值进行检测，实验平台测量结果见表5。

表5 实验平台的实测结果Tab.5 Measurement results on the test platform

由表5可知，基于本文提出方法测量的闪变包络系数和频率相对误差均小于1.5%，可有效实现电压闪变包络参数的准确检测。

5 结论

本文提出了基于自适应 VMD的方法，实现了非稳态电压闪变包络参数的准确检测和分析，仿真和实测结果表明：采用损失系数和能量差可准确判断 VMD模态分解个数；通过自适应 VMD实现了闪变包络信号的准确分解，有效避免了K值设置偏大或偏小带来的误差；本文方法在单一频率非稳态包络调制、幅值时变包络调制和多频率非稳态包络调制等情况下均具有较高准确度，且能获得非稳态电压闪变信号的时域信息，并有效克服了电网工频偏移、各类谐波和噪声的影响。相比现有检测方法，本文方法的检测精度更高，抗干扰性强，且克服了HHT存在的模式混淆问题，能有效实现复杂电网环境下的非稳态闪变包络参数准确检测，并为地震地质灾害检测、故障诊断、多频率调制信号分析等非稳态信号检测与分析研究提供新的借鉴。