基于综合灰关联序模型的残差门控循环神经网络位标器零部件选配
2021-02-22钟百鸿钟诗胜
钟百鸿 王 琳 钟诗胜
哈尔滨工业大学(威海)海洋工程学院,威海,264209
0 引言
装配作为位标器研制过程的关键环节[1],装配质量直接决定着位标器性能。漂移性能作为位标器一项关键性能,直接影响到制导武器的制导精度。
在位标器装配中,选配合适的零部件装配在一起,可改善位标器漂移性能。在位标器实际装配中,零部件一次选配成功率低,往往需要反复装拆选配与调试才能使其漂移性能达标。为提高位标器零部件装配效率,在装配开始前,以某一零部件的装配参数为输入,建立选配预测模型进行零部件匹配预测,实现零部件精确选配,可减少无效装配,提高装配效率、降低装配成本。
位标器零部件装配参数多,零部件选配又受到装配参数的影响,且影响程度未知,故这是一个典型灰色系统,灰关联理论正是针对这类灰色系统而提出的。PANG等[2]基于灰色系统理论,对影响装配失效的各种因素进行了综合评价和预测控制;SHETH等[3]利用灰色关联分析研究了切削速度、进给速度、切削深度等加工变量对加工效果的影响,并对这些参数进行了优化。通过对位标器装配数据进行灰关联分析,确定影响位标器零部件选配的关键装配参数是准确建立零部件选配预测模型的关键。另外,位标器装配参数之间存在非线性关系与复杂的耦合关系,单纯使用位标器动力学等理论推导零部件选配预测模型难以实现零部件选配。神经网络在建立具有复杂关系的预测模型中具备出色的性能,用来构建位标器复杂非线性的装配参数间映射关系模型非常合适。刘世平等[4]针对机械臂末端位姿信息与机械臂关节角度之间的复杂映射关系,建立BP神经网络解决机械臂逆运动学求解问题;贾振元等[5]基于BP神经网络与径向基神经网络(RBF)的混合预测模型,建立液压阀几何要素与其特性之间的复杂关系; LI等[6]采用卷积神经网络(CNN)与门控循环单元(gated recurrent unit,GRU)神经网络,建立了振动信号与齿轮故障之间复杂的映射关系。
本文以提高位标器零部件装配效率为目标,以位标器陀螺转子与调漂螺钉装配为例,在灰关联分析的基础上,建立综合灰关联序模型对陀螺转子装配数据进行关联分析,确定影响陀螺转子与调漂螺钉选配的关键装配参数;构建残差门控循环神经网络模型,建立陀螺转子装配参数与调漂螺钉质量之间的复杂映射关系,实现调漂螺钉质量的回归预测;基于预测结果实现陀螺转子与调漂螺钉的精确选配。
1 位标器陀螺转子装配数据关联分析
1.1 综合灰关联序模型构建
灰色关联分析[7](grey relational analysis,GRA)通过关联度顺序(grey relational order,GRO)来对因素间关系的强弱、次序进行描述,其基本思想是以因素的数据列为依据,用数学的方法研究因素间的几何对应关系。灰关联分析步骤如下。
(1)确定分析序列,以因变量为参考序列,自变量为比较序列,统称为变量序列。设参考序列为
X′0=(x′0(1),x′0(2),…,x′0(m))
(1)
式中,m为变量序列长度;x′0(m)为参考序列元素。
比较序列为
X′i=(x′i(1),x′i(2),…,x′i(m))T
(2)
式中,i=1,2,…,n;n为比较序列个数;x′i(m)为比较序列元素。
(2)变量序列的量纲一化。考虑到变量序列的量纲与取值范围一般不同,对变量序列进行量纲一处理,常用的方法有初值化法、均值化法、区间化法等。设变量经过量纲一处理后为
X=[X0X1…Xn]=
(3)
(3)计算X0对Xi在第k点的灰关联系数:
ζi(k)=
(4)
式中,k=1,2,…,m;ρ为分辨系数[8],0<ρ<1,通常ρ取值0.5[3],本文ρ取值0.5。
(4)参考序列与比较序列的关联度可用两序列各个点所对应的灰关联系数的平均值得到,即
(5)
(5)对关联度按大小进行排序,得到关联序。
文献[8]指出,采用灰关联分析时,灰关联序会受到量纲一处理方法的影响。为此,本文提出综合灰关联序(comprehensive grey relational order,CGRO)模型,综合考虑多种量纲一处理方法对关联序的影响。
综合灰关联序是在灰关联分析基础上,采用多种量纲一处理方法分别对变量进行处理,得到每种量纲一处理方法对应的关联序。先对每个变量对应的每种量纲一处理得到的关联序进行加和处理,得到加和关联序;然后对加和关联序按大小排序,即得到综合灰关联序。加和关联序计算公式为
(6)
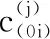
1.2 基于CGRO模型的位标器陀螺转子装配参数关联分析
陀螺转子与调漂螺钉作为位标器的关键零部件,二者之间的选配决定着位标器的漂移性能,二者装配简图见图1。调漂螺钉通过人工装配方式安装在陀螺转子顶部螺纹孔内,并使调漂螺钉底部与陀螺转子螺纹孔底部紧靠。调漂螺钉除长短不同外,其他属性一致,体现在装配参数上为调漂螺钉质量。陀螺转子与调漂螺钉的选配,实质上是通过选配合适质量的调漂螺钉与陀螺转子装配,使陀螺转子质心位置发生改变,使质心尽可能落在陀螺转子旋转轴上,进而改善位标器漂移性能。在实际装配中,陀螺转子需经过一系列测试,如动平衡测试、漂移测试等[9],装配人员根据测试情况选择合适的调漂螺钉与陀螺转子进行选配,使其漂移性能达标。这种人工选配、人工安装方式高度依赖装配人员经验,难以对装配过程中的拧紧力矩进行有效控制,且一次选配成功率低,需要反复装拆调整,造成位标器装配效率低、装配精度下降;同时,测试过程中的装配参数对陀螺转子与调漂螺钉选配有一定影响,但影响程度还未知,呈现出灰色系统特征。通过本文建立的综合灰关联序模型对陀螺转子装配数据进行关联分析,找出影响陀螺转子与调漂螺钉选配的关键装配参数,在实际装配环节中进行严格管控,对提高位标器装配质量有着重要意义。
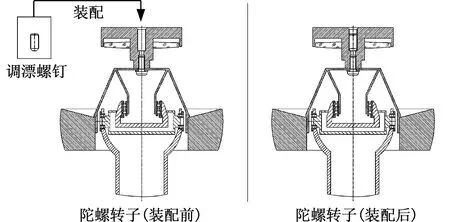
图1 陀螺转子与调漂螺钉装配简图Fig.1 Assembly diagram of gyro rotor and drift-adjusting screw
陀螺转子测试中涉及的相关装配参数主要有11项,具体为初始动平衡量、后配重大小、后配重位置、前配重大小、前配重位置、调试后动平衡量、+X方向初始漂移值、+Y方向初始漂移值、+Z方向初始漂移值、-Y方向初始漂移值、-Z方向初始漂移值。将调漂螺钉质量参考序列设为X′0,陀螺转子其余11项装配参数作为比较序列X′i(i=1,2,…,11)。
考虑到不同量纲一处理方法对关联序的影响,本文采用常用的3种量纲一方法进行数据规范化,分别为初值化法、均值化法、区间化法。
(1)初值化处理:
(7)

(2)均值化处理:
(8)
(3)区间化处理:
(9)

收集到528个位标器装配样本,部分原始数据见表1,应用所提CGRO模型对陀螺转子11项装配参数与调漂螺钉质量进行关联分析。先对原始数据进行3种量纲一处理,然后计算每种量纲一处理方法对应的参考序列与比较序列的灰关联系数、灰关联度,得到3种关联序,进而得到加和关联序、综合灰关联序,最后通过综合灰关联序确定影响陀螺转子与调漂螺钉选配的关键装配参数。若加和关联序相同,则视为同等重要。实验结果见表2。
实验结果表明,采用不同的量纲一处理方法对变量进行初始化处理,得到的关联序不同,这与有关文献的论述一致[8]。采用初值化、均值化、区间化这3种量纲一处理方法,得到的关联序确定出前4项影响陀螺转子与调漂螺钉选配的关键装配参数均为-Z、-Y、+Z、+Y初始方向漂移值;确定第5项关键装配参数时,根据初值化关联序得到的是前配重位置,而均值化与区间化则为调试后动平衡量;确定第6项关键装配参数时,初值化得到的为后配重位置,均值化则为后配重大小,区间化则为前配重位置。可见,采用不同量纲一处理方法对变量进行初始化处理得到的关联序不同,难以确定因素的相对主次顺序。

表1 部分原始数据
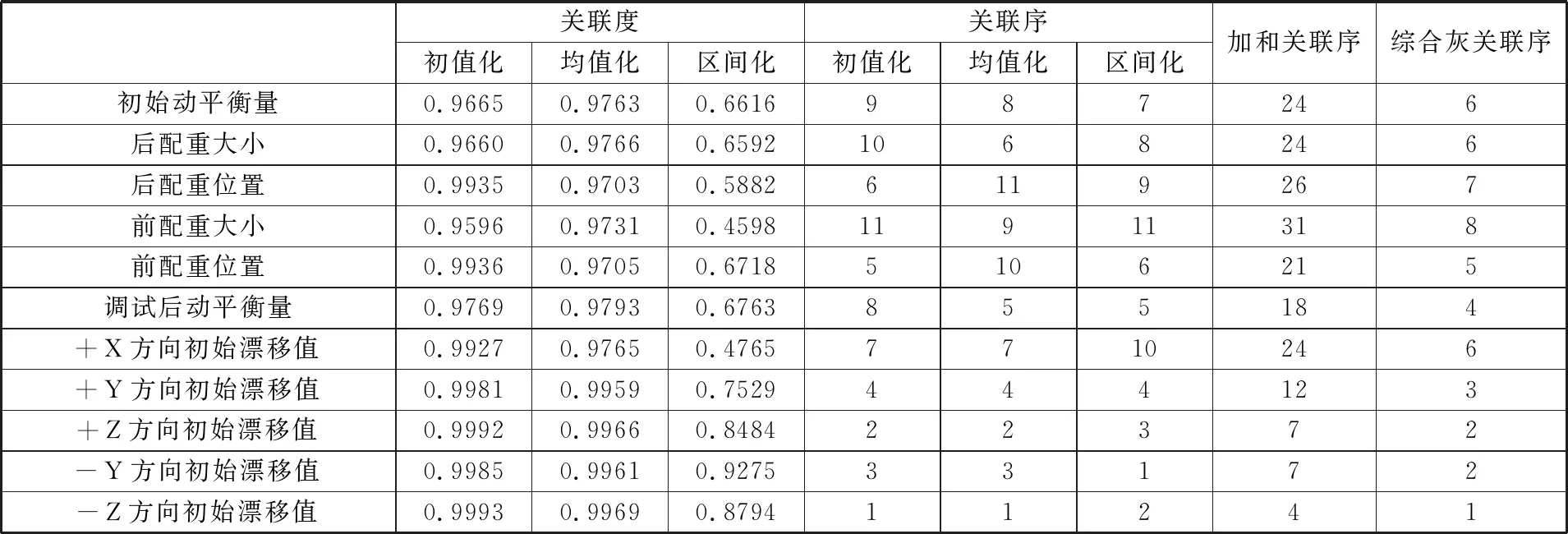
表2 陀螺转子装配参数综合灰关联分析结果
通过本文提出的综合灰关联序模型,可以综合考虑采用各量纲一处理方法对变量进行初始化处理后得到的关联序,给出影响调漂螺钉与陀螺转子装配的装配参数的相对主次顺序,依次为:-Z方向初始漂移值、-Y方向初始漂移值(+Z方向初始漂移值,两者重要程度相当)、+Y方向初始漂移值、调试后动平衡量、前配重位置、+X方向初始漂移值(后配重大小、初始动平衡量)、后配重位置、前配重大小。
通过综合关联序模型得出的结论与各量纲一处理方法得出结论相比,综合关联序模型的优势在于:
(1)各量纲一处理方法对变量进行初始化处理后得到的关联序不同,难以确定最终的因素相对主次影响程度,而综合关联序模型则是在各量纲一处理方法得到的关联序的基础上给出的关联序,既考虑了单一量纲一处理得到的关联序,又考虑了各量纲一处理得到的关联序的综合作用,给出的综合关联序明确了各因素的相对主次影响程度,更具参考意义。
(2)综合关联序确定的前4项关键装配参数与各量纲一处理方法得到的一致,确定的第5项关键装配参数与均值化、区间化确定的相同,均为调试后动平衡量,而初值化确定的为前配重位置;确定的第6项关键装配参数与区间化确定的相同,均为前配重位置,而初值化与均值化确定的分别为后配重位置、后配重大小。对本文分析的装配参数来说,综合关联序模型得出的结果比单一量纲一处理方法得到的结果更能反映出实际情况。
以往装配人员主要根据+Y、+Z、-Y、-Z这4个方向初始漂移值来选择调漂螺钉与陀螺转子进行装配,通过综合关联分析可以得到,这4个方向初始漂移值对调漂螺钉与陀螺转子装配的影响确实很大,符合实际装配情况;同时发现,陀螺转子调试后动平衡量、前配重位置这2项装配参数对调漂螺钉的装配影响也很大,这2项装配参数需要在装配环节中进行严格管控,从而提高产品装配质量。
2 残差门控循环神经网络选配预测模型构建
陀螺转子装配参数与选配的调漂螺钉质量之间存在着复杂非线性映射关系,难以建立明确的函数关系式,且装配数据之间还存在依赖关系。循环神经网络通过隐藏或记忆状态引入数据前后信息之间的依赖关系,以保存当前状态的关键信息,并通过反向传播方式训练网络;残差神经网络中残差块的设计可以很好地缓解神经网络反向传播时出现梯度消失和梯度爆炸的问题。结合循环神经网络与残差神经网络的优点,构建残差循环神经网络,以基于CGRO确定的陀螺转子关键装配参数作为神经网络的输入,调漂螺钉质量为输出,进行调漂螺钉质量回归预测,实现陀螺转子与调漂螺钉的精确选配,从而提高位标器零部件一次装配成功率与装配精度。
2.1 门控循环神经网络
门控循环神经网络[10-11]是循环神经网络的一种变体,它通过引入门控机制来保存当前状态信息对之前状态信息的依赖,其单元结构如图2所示。图2中,x(t)、h(t)、r、z、c分别表示t时刻单元的输入、输出、重置门、更新门与短期记忆,σ为Python-Spyder软件中的sigmoid激活函数。更新门决定了保留上一单元记忆信息的多少,重置门将新的输入与上一单元的记忆信息结合起来。GRU单元更新公式如下:
z=σ(Wzh(t-1)+Uzx(t))
(10)
r=σ(Wrh(t-1)+Urx(t))
(11)
c=tanh(Wc(h(t-1)⊗r)+Ucx(t))
(12)
h(t)=(z⊗c)+((1-z)⊗h(t-1))
(13)
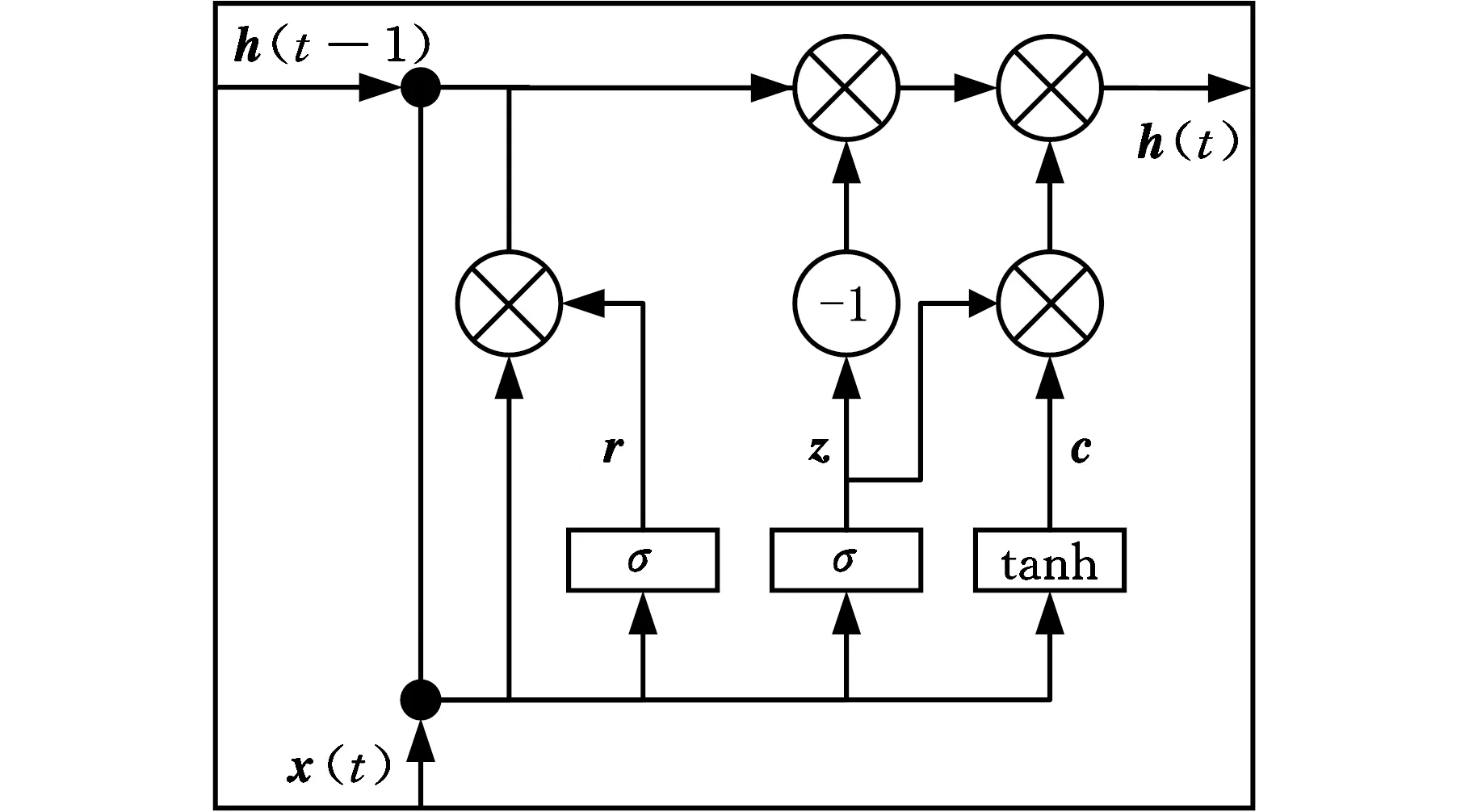
图2 GRU结构网络示意图Fig.2 Schematic diagram of GRU
式中,(Wz,Uz)、(Wr,Ur)、(Wc,Uc)分别为GRU更新门、重置门、短期记忆单元的状态与输入权重参数;⊗为矩阵乘法。
2.2 残差神经网络
训练神经网络的最大挑战在于神经网络涉及反向传播时容易出现梯度消失和梯度爆炸的现象,而残差神经网络[12-13](residual networks,RN)中的残差块设计可以有效减缓这种情况,图3所示为2层残差块结构。
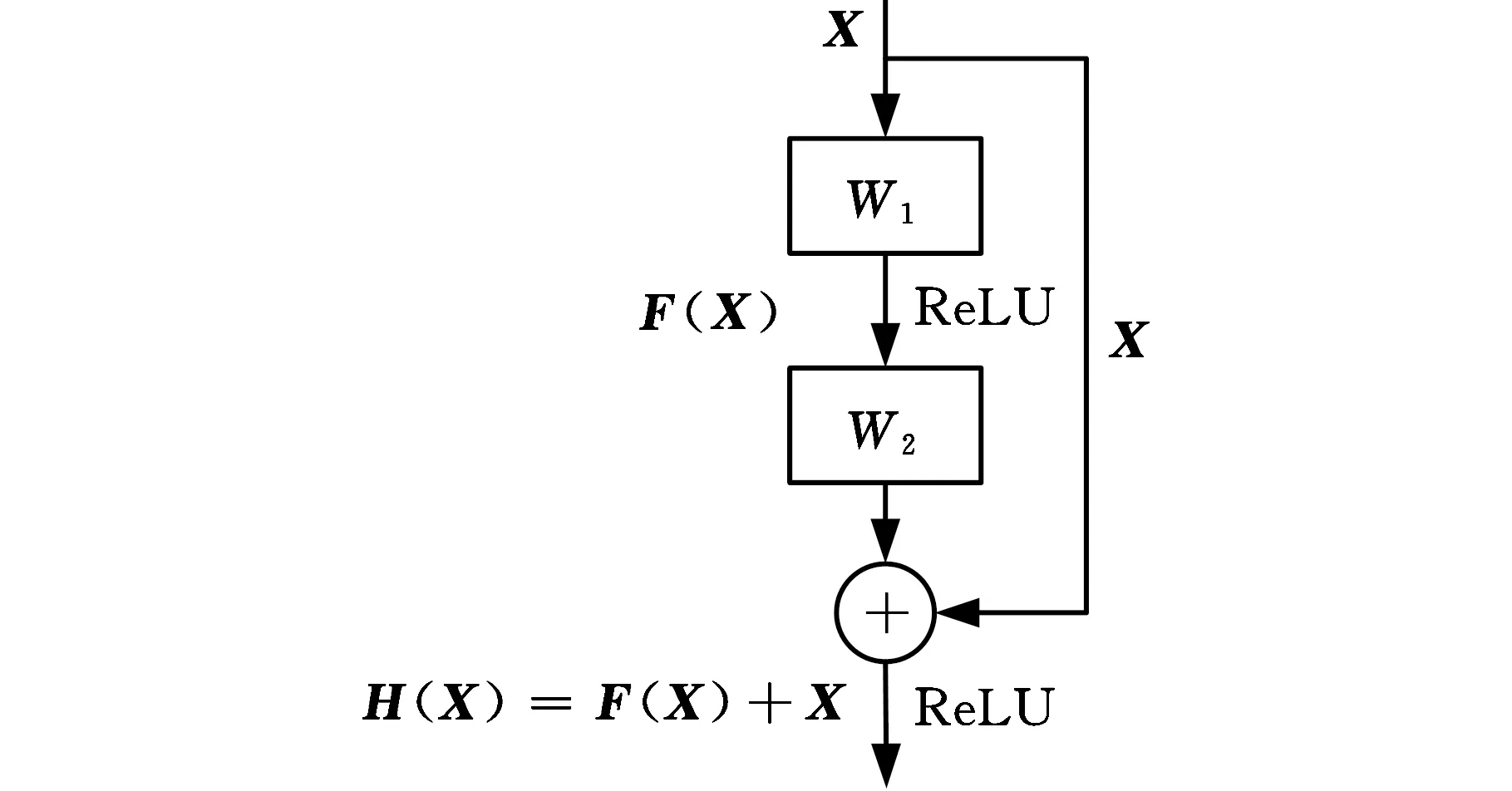
图3 残差块结构示意图Fig.3 Schematic diagram of residual learning
图3中,X为残差块输入,W1、W2分别为残差块的权重层,F(X)表示求和前神经网络映射的残差,H(X)表示求和后神经网络映射的残差,假设Y为残差块的输出,则有
F(X)=W2α(W1X)
(14)
Y=α(F(X)+X)
(15)
式中,α为ReLU激活函数。
2.3 残差门控循环神经网络
结合门控循环神经网络与残差神经网络优点,建立残差门控循环神经网络(RNGRU),模型简图见图4。
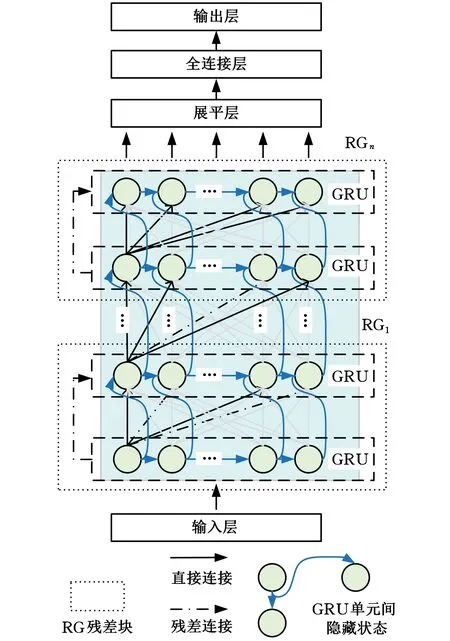
图4 RNGRU神经网络模型结构Fig.4 Schematic diagram of RNGRU
RNGRU与传统残差神经网络的不同在于:RNGRU中的残差块主要由GRU单元组成。RNGRU与传统GRU神经网络的不同在于:相比于传统多个GRU单元堆叠而成的GRU神经网络,RNGRU在多个GRU单元之间多了残差连接模块。
3 实验与结果
实验样本来源为528个某型号导弹位标器的装配样本数据,按4∶1比例随机划分训练集与测试集,部分数据见表1。
在CGRO分析基础上,设计4组实验,分别以CGRO确定的3、4、5、6项关键装配参数为RNGRU的输入,输出为调漂螺钉质量,4组实验简记为CGRO-3、CGRO-4、CGRO-5、CGRO-6。
为消除陀螺转子装配参数之间因量纲不同以及数据取值范围不同带来的影响,对装配数据进行预处理:

实验评价指标采用平均绝对误差(mean absolute error,MAE)eMA、均方误差(mean squared error, MSE)eMS,计算公式如下:
(17)
(18)
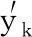
实验操作平台为Windows 10,软件工具为Python。实验参数设置见表3,得到的实验结果见表4和图5、图6。

表3 RNGRU模型参数

表4 调漂螺钉RNGRU神经网络预测实验结果
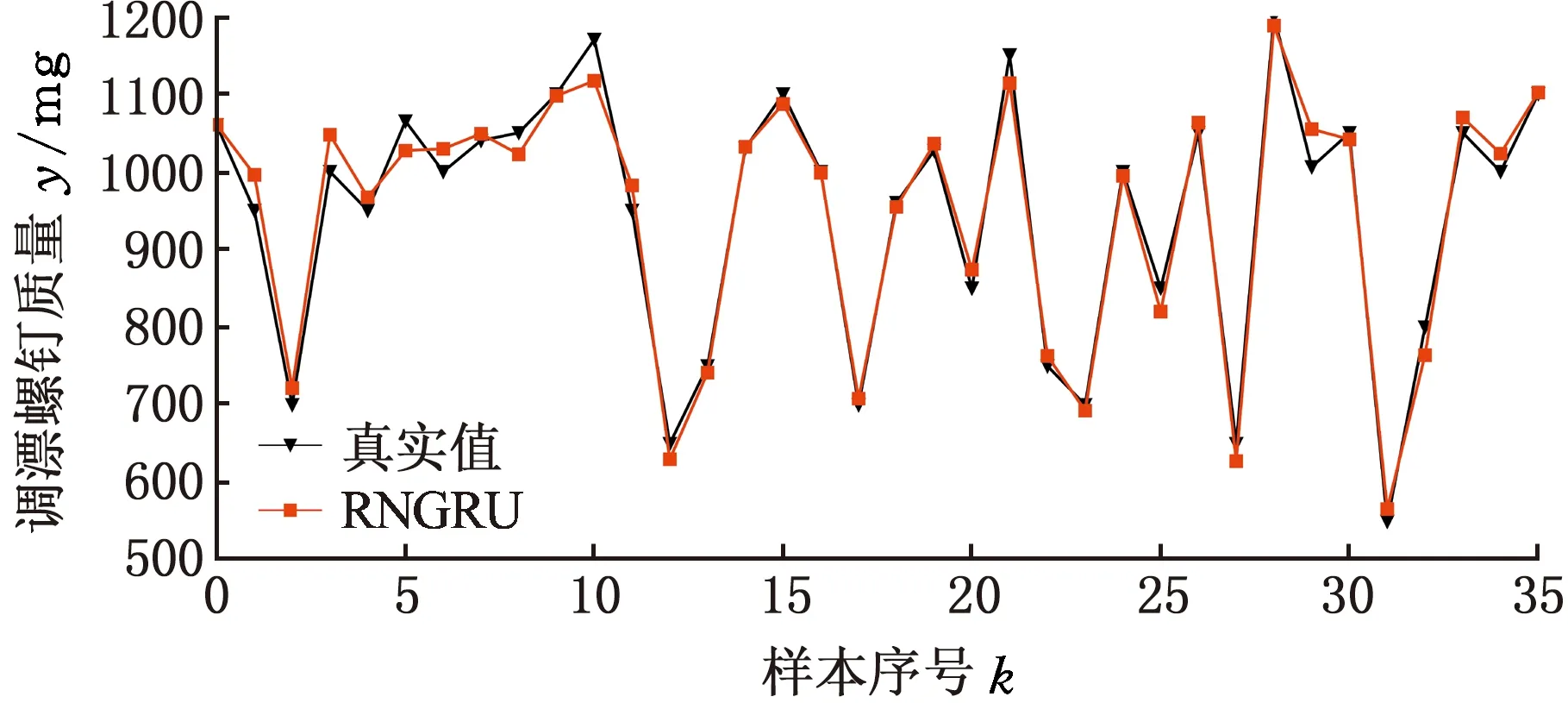
图5 部分调漂螺钉质量RNGRU神经网络预测结果Fig.5 The partial RNGRU prediction results for the mass of drift-adjusting screw
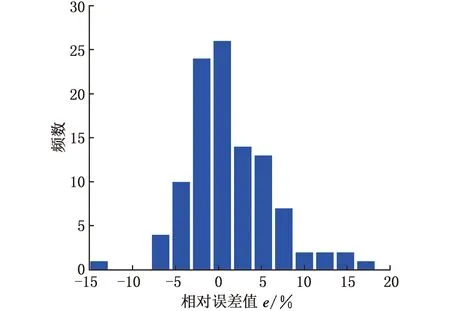
图6 RNGRU模型预测结果相对误差值分布直方图Fig.6 Histogram of relative error distribution of the RNGRU prediction results
表4中,标注加粗部分为实验最优结果,图5所示为CGRO-5实验部分调漂螺钉质量RNGRU神经网络预测值与真实值对比。结合表4及图5实验结果可知:CGRO-5得到的实验结果最优,其MAE、MSE均比CGRO-3、CGRO-4、CGRO-6的结果好;CGRO-3、CGRO-4实验结果较差可能在于以3或4项装配参数作为输入训练神经网络,得到的信息量不足;CGRO-6实验结果不太理想可能在于所选的参数中存在冗余信息,影响了神经网络预测精度。
从图5中可以看到,采用RNGRU神经网络进行陀螺转子选配调漂螺钉预测是可行的,其预测结果能很好地反映出实际陀螺转子选配调漂螺钉的情况,但存在部分预测值与实际值偏差较大的情况,原因一方面在于神经网络训练样本量受限,另一方面是实际选配调漂螺钉质量使位标器漂移性能达标即可,没有确定的量化评价指标,使得选配的调漂螺钉质量可以在一定范围内波动。
由图6可以看出,RNGRU模型预测结果的相对误差大部分控制在±5%以内,且绝大部分在±10%以内,考虑到调漂螺钉质量可以在一定范围内波动,即使调漂螺钉质量预测值与真实值存在误差,在误差不大的情况下,根据RNGRU预测的调漂螺钉质量与陀螺转子装配,也能使陀螺转子漂移值满足要求,说明RNGRU预测模型具有较高的准确度。
根据以上4组实验得到的实验结果,在CGRO-5基础上还进行了多组不同方法的对比实验,对比实验中神经网络模型参数保持一致,其中支持向量机(SVM)模型参数通过网格搜索法寻优确定,得到的实验结果见表5、表6与图7、图8。

表5 调漂螺钉质量预测实验结果对比
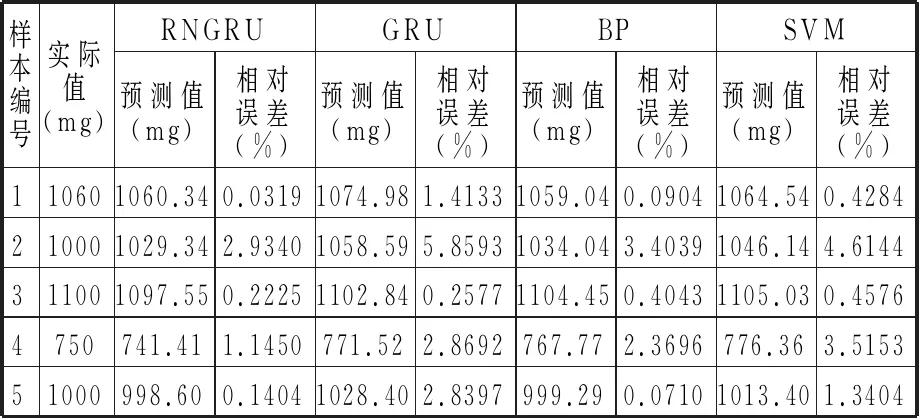
表6 部分实验调漂螺钉质量预测结果对比
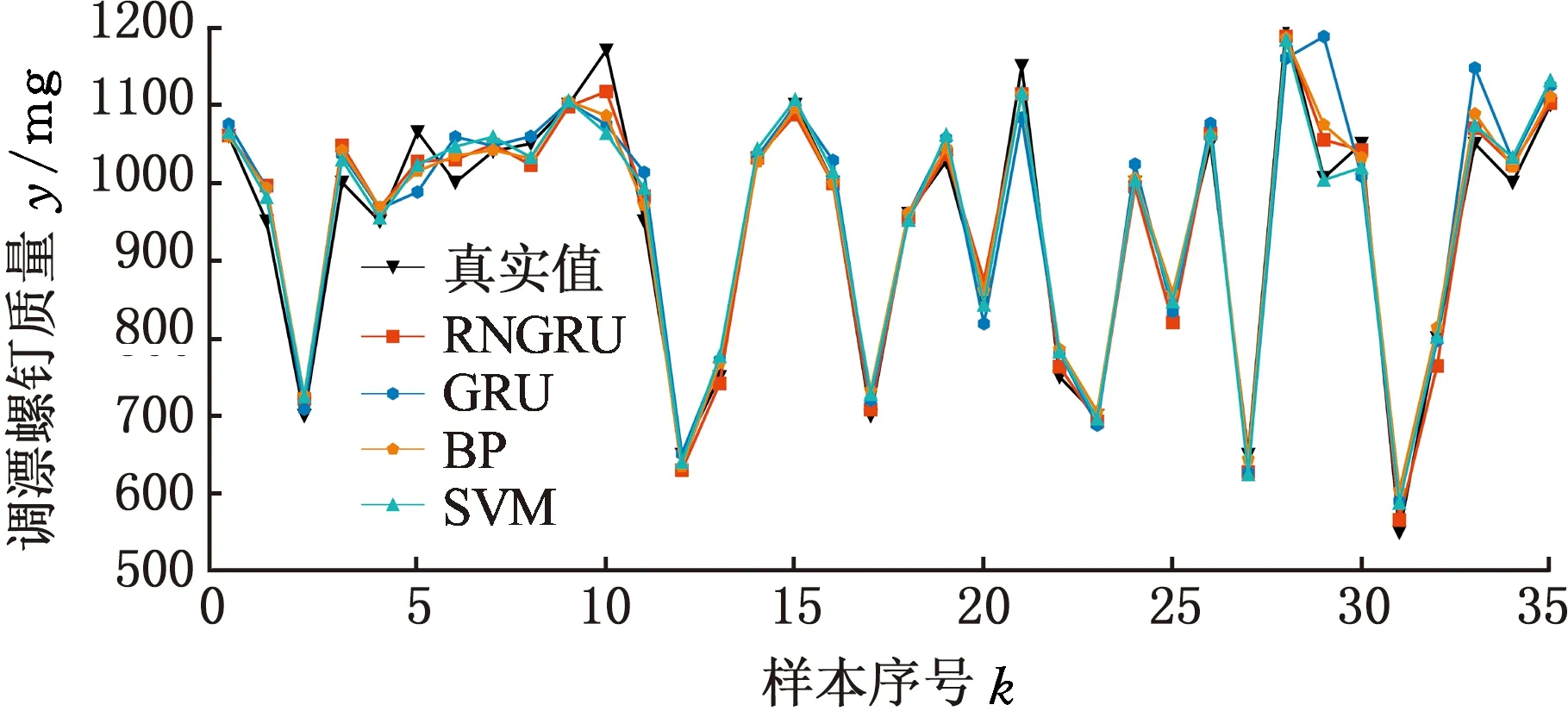
图7 不同方法下部分调漂螺钉质量预测结果对比Fig.7 The partial result comparisons of different methods for the mass of drift-adjusting screw
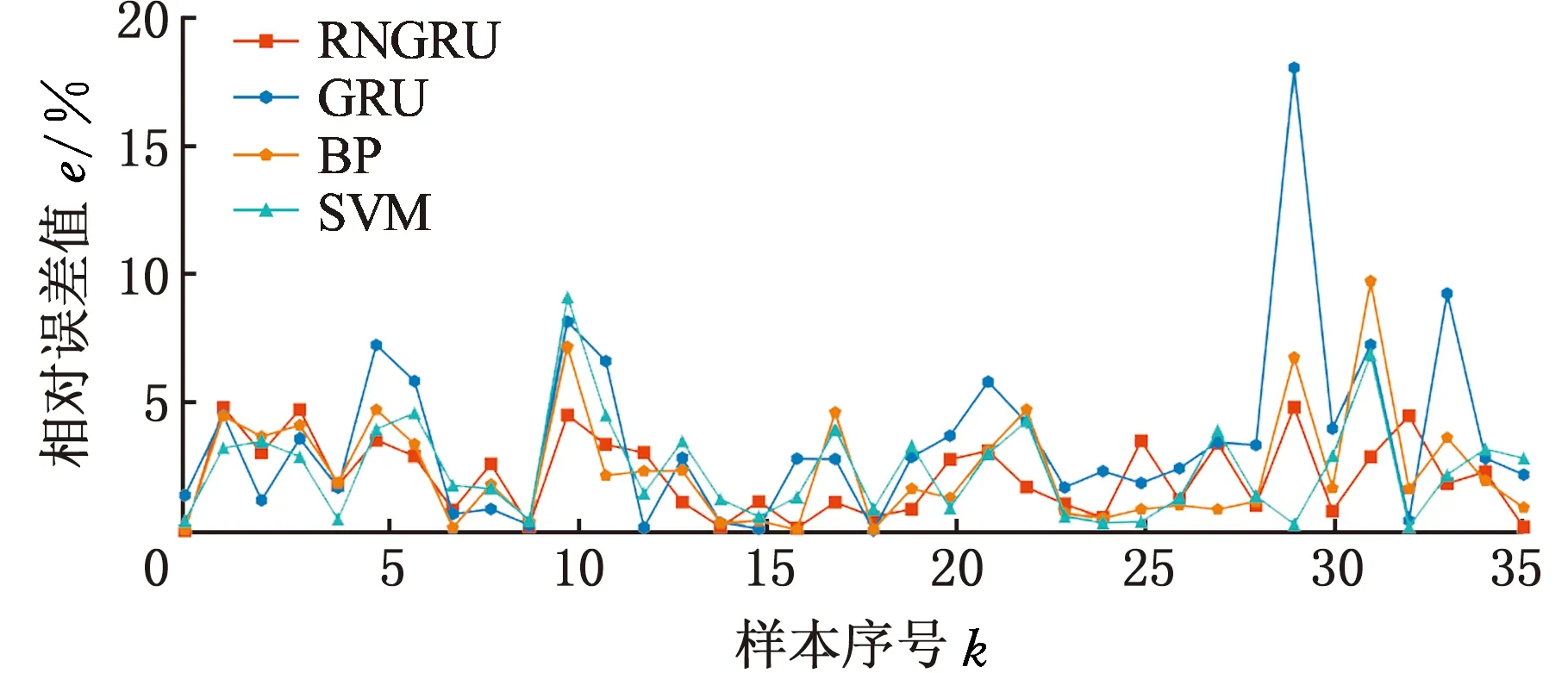
图8 不同方法下部分相对误差值对比Fig.8 Comparison of partial relative error values under different methods
表5中,SVM中核函数为径向基函数;标注加粗部分为本文所提方法与实验最优结果。从表5中可知:RNGRU方法得到的实验结果最佳,其MAE、MSE均是最优值;RNGRU方法与传统GRU神经网络相比,其MAE值降低了10.2%,MSE值降低了13.9%,说明在传统的GRU神经网络模型中,加入残差块设计的RNGRU模型具备更好的预测能力,进一步突出本文所提方法的优越性。
观察表6与图7、图8可得,本文所提方法RNGRU得到的预测值曲线与真实值曲线变化基本一致,其平均相对误差值更小。
4 结论
(1)本文提出一种基于综合关联序(CGRO)模型的残差门控循环神经网络(RNGRU)位标器零部件选配方法,该方法通过CGRO模型得到陀螺转子关键装配参数,以此建立RNGRU选配预测模型,进行调漂螺钉质量的回归预测,从而实现陀螺转子与调漂螺钉的选配,可用于引导装配人员进行位标器零部件装配,提高位标器零部件装配效率并降低装配成本。
(2)提出一种综合关联序模型,该模型综合考虑各量纲一处理方法对关联序的影响。在位标器零部件装配参数的关联分析中,采用综合关联序模型得到的结论更符合实际装配情况。
(3)提出一种残差门控循环神经网络,该网络在传统的门控神经网络基础上加入残差块结构,在本文的预测结果中,所提残差门控循环神经网络具备最好的预测能力。
