考虑道路坡度与车辆载重的纯电动物流车综合性能换挡规律

李聪波 张 弛 屈世阳 胡曾明

重庆大学机械传动国家重点实验室，重庆，400030

0 引言

随着世界环境污染和能源危机的不断加重，纯电动汽车因其使用清洁能源且污染小的特点受到越来越多的关注。现有纯电动汽车绝大多数使用固定速比减速器，无法同时满足车辆对动力性与经济性的需求，而使用多挡变速器对驱动电机的工作区间进行调节，可降低对驱动电机的性能要求，同时制定合适的换挡规律可有效提升车辆的动力性与经济性[1]。因此有学者针对纯电动汽车的换挡规律进行了相关研究。根据换挡规律制定的方式，可将其分为静态换挡规律与动态换挡规律。静态换挡规律是根据驱动电机/发动机与车辆的稳态数据制定的稳态工况换挡规律；动态换挡规律是指在考虑车辆稳态数据的基础上，进一步分析驾驶环境与车辆动态变化对换挡规律的影响，从而制定的具有动态适应性的换挡规律。

在静态换挡规律方面，ZHU等[2]提出一种基于稳态电机效率的动力性与经济性换挡规律制定方法，通过仿真与硬件在环试验验证了该方法的有效性；高玮等[3]针对纯电动公交车，应用动态规划优化方法对车辆的换挡策略进行优化，得到的两参数换挡规律有效降低了车辆在5种驾驶循环工况下的能耗；WANG等[4]将变速系统结构参数与经济性换挡规律进行集成优化，使得车辆在NEDC与UDDS循环工况下的续航里程得到较大增加；陈淑江等[5]针对动力性与经济性换挡规律的差异进行研究，制定了兼顾汽车动力性与经济性的换挡规律并进行仿真验证，结果表明车辆的性能得到了一定提升。上述对换挡规律的研究皆属于静态范畴，然而实际中的驾驶环境复杂多变，同时车辆自身的状态也会发生变化，传统的静态换挡规律无法根据这些变化进行动态调整，导致车辆不能以最优换挡规律进行换挡，因此有学者对动态换挡规律进行了研究。

在动态换挡规律方面，道路坡度与车辆载重是影响车辆动态性能的主要因素。LIU等[6]构建了动态行驶环境下的纯电动汽车能耗预测模型，研究指出道路坡度对车辆的经济性有显著影响；CARLSON等[7]的研究表明，车辆质量的变化也对车辆的经济性能有显著影响；KIDAMBI等[8]指出，道路坡度与车辆质量变化均会引起车辆行驶阻力的变化，从而影响车辆的动力性能。因此有部分学者在制定换挡规律时考虑道路坡度对换挡规律的影响，制定具有坡道适应性的动态换挡规律。LU等[9]制定了考虑道路坡度的多性能指标动态换挡规律，并在坡道工况下进行仿真验证，结果表明制定的动态换挡规律相比于静态换挡规律可提升车辆在动态环境下行驶的经济性；GUO等[10]通过实时采集车辆的状态信息与道路坡度信息，对车辆的换挡规律进行实时计算，有效提高了车辆在坡路上行驶时的能量效率；MENG等[11]制定了考虑上坡工况动力性、下坡工况安全性和缓坡工况经济性的动态换挡策略，改善了车辆在坡道工况下行驶的动力性与经济性。车辆载重变化会引起整车质量的变化，同样会对换挡规律产生影响，部分学者在制定换挡规律时同时考虑了道路坡度与车辆载重两个影响因素。夏光等[12]提出了自动变速器坡道换挡分层修正控制策略，利用道路坡度信息与车辆质量信息对换挡规律进行动态修正，提高了车辆对坡道工况的适应性。

分析以上文献可以看出，道路坡度与车辆载重的变化均会对车辆的动力性与经济性产生影响，一类研究未考虑道路坡度与车辆载重制定了综合性能换挡规律，另一类研究考虑道路坡度或车辆载重制定了动力性与经济性换挡规律，无法同时兼顾车辆加速性能及低能耗的需求。本文针对纯电动物流车在不同道路坡度与载重的驾驶条件下制定兼顾车辆动力性与经济性的综合性能换挡规律，提高车辆对动态驾驶环境的适应性，提高纯电动物流车的动力性能，延长其续航里程。

1 考虑道路坡度与车辆载重的换挡规律框架

1.1 问题描述

传统的车辆换挡规律是基于车辆自重不变与平路工况制定的，从而获得车辆最佳动力性或最佳经济性换挡规律。由于传统的静态换挡规律缺乏对动态驾驶环境的适应性，当车辆行驶的道路坡度与车辆载重发生变化时，车辆受到的坡道阻力与行驶阻力均会发生变化，车辆此时若仍然使用传统的静态换挡规律进行换挡，则会出现循环换挡或意外换挡的现象，降低车辆行驶的舒适性与安全性，同时还会导致车辆在坡道上行驶时动力不足，无法在最佳时机进行换挡，降低车辆的动力性与经济性。

纯电动物流车主要用于城市内部与城市间的物流运输，其载重变化较大，在城市中行驶时常会遇到坡路与高架桥等行驶路况，此时车辆载重对换挡规律的影响更为突出。

可换挡的纯电动乘用车一般为两挡，而纯电动物流车主要用于运输货物，相对于纯电动乘用车具有自重大、载重变化较大的特点。纯电动物流车在爬坡时需要变速系统进行高转矩输出，在城市间高速行驶时需高转速输出，这需要变速系统具有较宽的传动比范围来适应车辆的行驶条件。为保证换挡顺畅，最大与最小传动比的比值不宜过大，故在应用于纯电动物流车的变速箱中设计3个挡位，对应车辆载货爬坡、城市货物运输和高速行驶的驾驶条件，满足纯电动物流车对转矩与转速的要求。课题组前期提出一种纯电动物流车三挡变速系统，该变速系统应用了行星齿轮系+平行轴结构布局，通过改变传动比可扩大驱动电机高效区间与高转矩区间对应的车速范围，三挡变速系统结构如图1所示。图1中，M表示驱动电机，B1与B2表示制动器，S表示太阳轮，P表示行星轮，R表示齿圈，PC表示行星架，C1与C2表示离合器，通过改变各离合器与制动器的工作状态形成3个挡位，对驱动电机的工作区间进行调节，以适应不同的车辆行驶工况。三挡变速系统工作模式如表1所示。

图1 三挡变速系统结构Fig.1 The structure of three-speed transmission system

表1 三挡变速系统工作模式

1.2 纯电动三挡物流车换挡规律框架

合理的换挡规律既能保证车辆的动力性能，又能提高驱动电机的工作效率，延长续航里程。本文提出一种考虑道路坡度与车辆载重的综合性能换挡规律制定方法，换挡规律框架如图2所示。

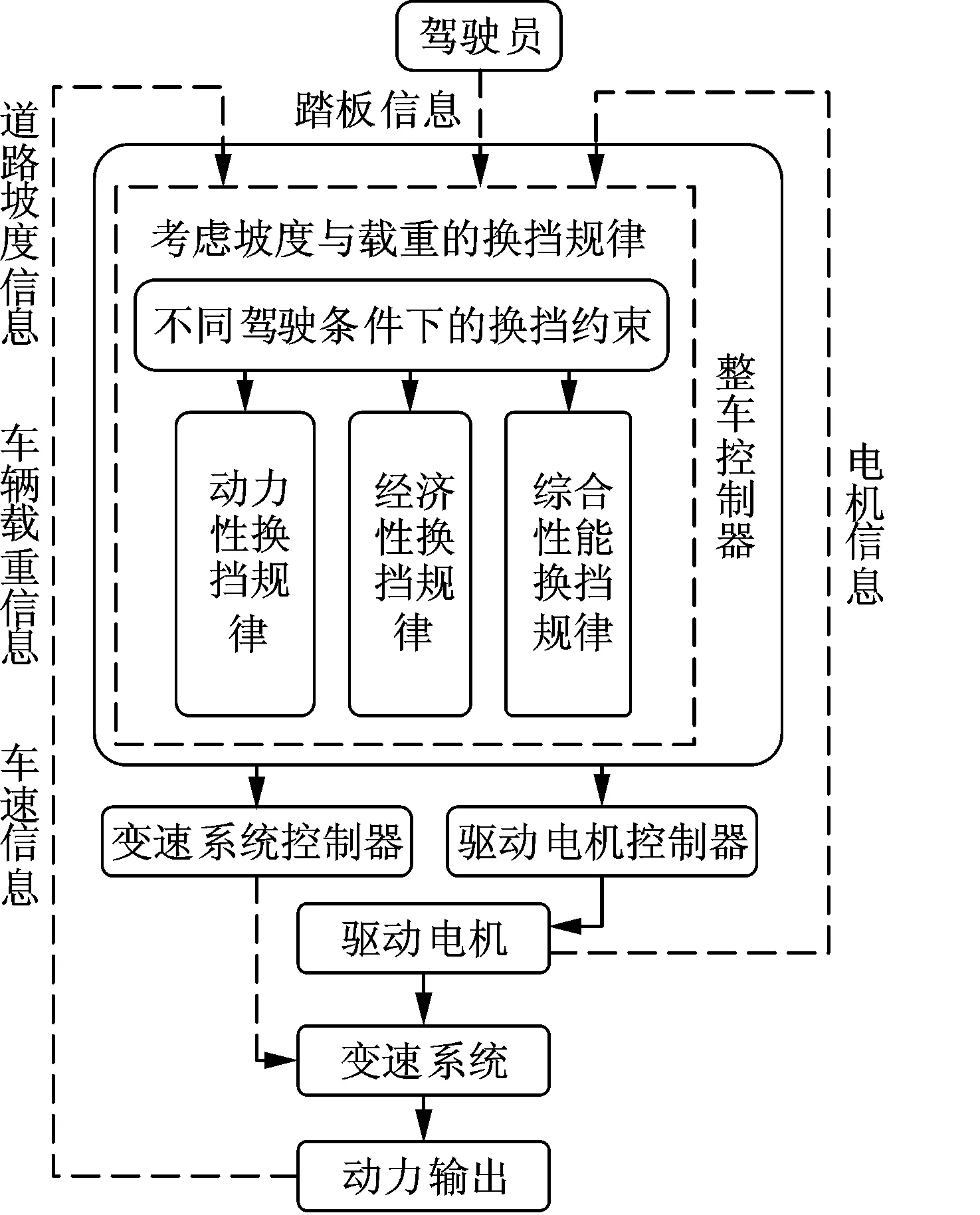
图2 换挡规律框架Fig.2 Framework of shift schedule

(1)不同驾驶条件下的换挡约束。分析道路坡度与车辆载重对换挡规律的影响，得到不同道路坡度与车辆载重下的换挡规律约束。

(2)考虑道路坡度与车辆载重的换挡规律制定。综合考虑道路坡度与车辆载重对车辆换挡规律的影响，分别制定考虑道路坡度与车辆载重的纯电动三挡物流车动力性换挡规律与经济性换挡规律。

(3)考虑道路坡度与车辆载重的综合性能换挡规律优化。建立动力性与经济性的换挡规律协同优化模型并进行求解，得到不同驾驶条件下的综合性能换挡规律。

以重庆某汽车有限公司某型号纯电动物流车为研究对象，其动力性指标为：满载最高车速vmax=90 km/h，0～50 km/h加速时间ta=12 s，最大爬坡度Imax=30%，该纯电动物流车的整车基本参数如表2所示，其三挡动力系统参数如表3所示。

表2 整车参数

表3 动力系统参数

2 道路坡度与车辆载重对行驶阻力的影响分析

当车辆处于行驶过程中时，驱动电机提供的驱动力Ft需克服车辆的行驶阻力F，行驶阻力包括来自路面的行驶阻力Ff、车辆表面与空气相互作用产生的空气阻力Fw、由重力产生的坡道阻力Fi和车辆加速时产生的加速阻力Fj。车辆的动力学平衡式可表示为

(1)

式中，mc为载货质量；β为坡道的倾角；δn为车辆第n挡的旋转质量换算系数。

根据我国JTG D20—2006《公路路线设计规范》与CJJ 37—2012《城市道路工程设计规范》可知，公路最大纵坡不可超过9%，特殊情况下不可超过10%。本文所研究的纯电动物流车多在城市道路与路面良好的高速公路上行驶，考虑现行公路建设标准与城市地下停车场出入口坡道的实际情况，选择17.6%为车辆在城市中行驶的最大坡道纵向坡度[12]，载货车辆的极限性能指标要求爬坡度达到30%。

图3为车辆以100%踏板开度行驶时的驱动力矩与行驶阻力矩对比图。车辆在空载状态下，2挡提供的驱动力矩大于车辆在坡度为17.6%的坡道上行驶时产生的阻力矩，而3挡提供的驱动力矩不足以克服同等行驶阻力矩，为保证车辆的坡道通过性，不进行2-3升挡操作。随着道路坡度的增加，满载车辆受到的阻力矩相对于空载时的增幅更大，在坡度为17.6%的行驶条件下，满载车辆的2挡驱动力矩不足以克服车辆行驶的阻力矩，不进行1-2升挡操作。

图3 驱动力矩-行驶阻力矩对比图Fig.3 Comparison diagram of driving torques and driving resistance moments

若车辆换挡后的驱动力矩小于阻力矩，便会发生意外降挡与换挡循环，产生的转矩波动会降低驾驶舒适性，同时还会加剧变速系统的磨损，降低零件使用寿命，因此换挡规律应进行相应的调整，当下一挡位提供的驱动力矩不足以克服行驶阻力矩时，变速系统不进行升挡操作。

3 考虑道路坡度与车辆载重的换挡规律制定

换挡规律决定了车辆行驶时的挡位选择，直接影响动力系统的工作状态，从而影响车辆的动力性与经济性。传统的两参数换挡规律以踏板开度与车速作为换挡决策参数，为提升车辆对驾驶环境的适应性，本文在制定换挡规律的过程中加入道路坡度与车辆载重两个参数，制定考虑道路坡度与车辆载重的动态换挡规律。

3.1 动力性换挡规律制定

动力性换挡规律要保证车辆在行驶过程中具有良好的动力输出能力，满足车辆在极限工况下对动力输出的要求，选择不同挡位下，相同道路坡度、车辆载重与踏板开度下车辆加速度相等的车速作为换挡车速。换挡点求解表达式为

(2)

式中，in为变速系统第n挡的传动比；k为踏板开度。

图4为载货质量mc=0，踏板开度k=70%时各挡位的车辆加速度曲面，最大加速度为2.571 m/s2，不同挡位的加速度曲面相交得到的曲线即为踏板开度k=70%的动力性换挡曲线。将各踏板开度与不同驾驶条件下的升挡曲线进行拟合，同时根据换挡约束对动力性换挡规律进行修正，即可得到不同道路坡度与载重条件下的车辆动力性换挡曲面，如图5、图6所示。

图4 车辆空载、k=70%时各挡位加速度曲面Fig.4 The acceleration surface of each gear when the electric vehicle is no-load, k=70%

图5 不同驾驶条件下1-2升挡曲面(动力性)Fig.5 1-2 shifting surface under different driving conditions(dynamic)

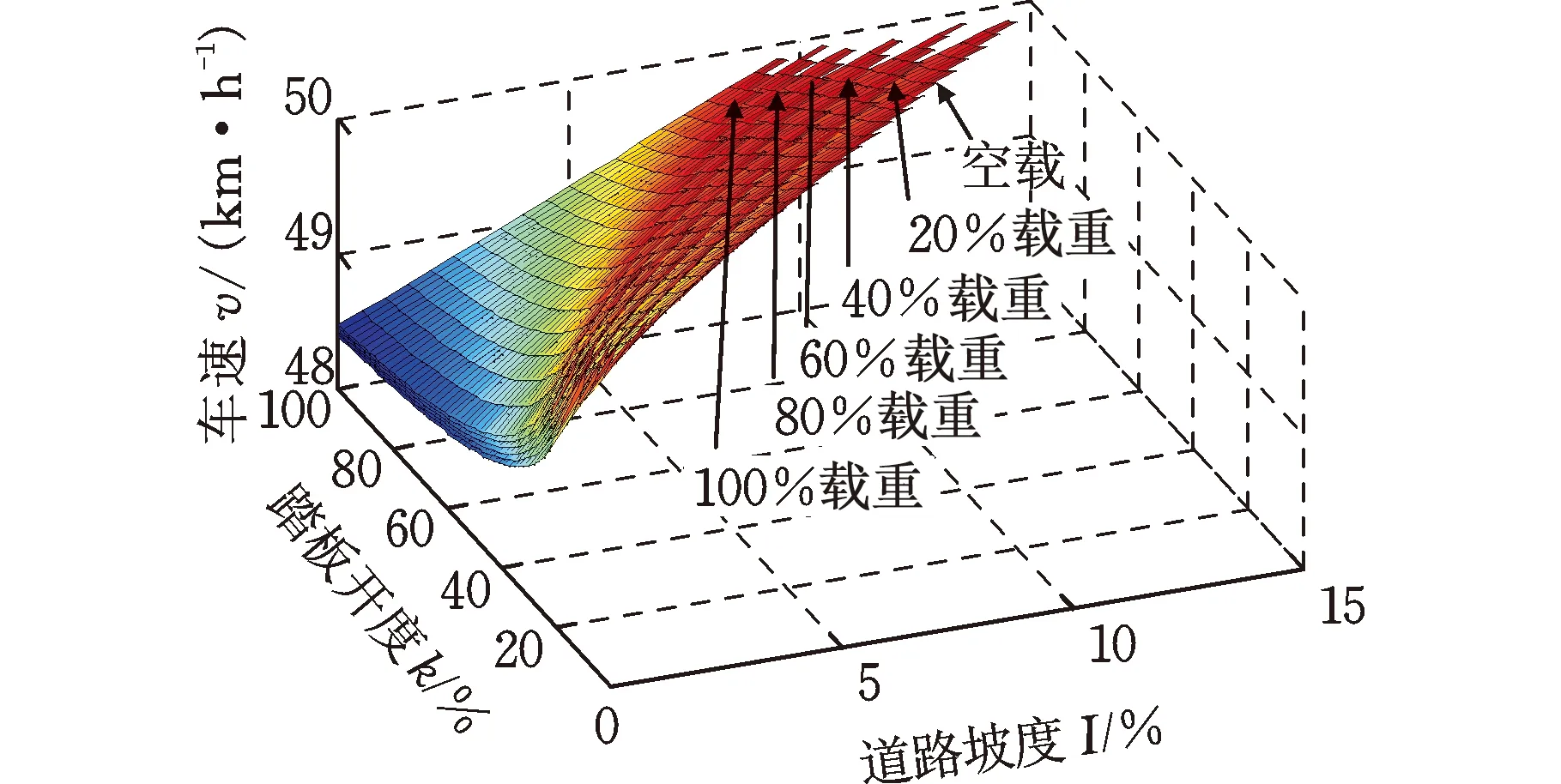
图6 不同驾驶条件下2-3升挡曲面(动力性)Fig.6 2-3 shifting surface under different driving conditions(dynamic)

由图5与图6可看出，换挡车速随着道路坡度与车辆载重的增大而提高。随着车辆载重的增大，1-2挡可进行换挡的最大道路坡度由26.23%减小至17.07%，2-3挡可进行换挡的最大道路坡度由14.86%减小至9.94%。

3.2 经济性换挡规律制定

经济性换挡规律应保证在车辆行驶过程中驱动电机尽可能地运行在高效区间，提高驱动电机的能量利用率，从而降低车辆能量消耗并延长车辆的续航里程。因此车辆在不同道路坡度与车辆载重驾驶条件下的换挡点选择应尽量使驱动电机的效率保持连续，选择相同道路坡度、车辆载重、踏板开度，不同挡位下，驱动电机效率相等的车速作为换挡车速，求解表达式为

ηM|(k,mc,β,in)=ηM|(k,mc,β,in+1)

(3)

驱动电机效率可使用如下经验公式进行计算：

(4)

式中，Pi为驱动电机在任意工作状态下的输出功率；ni为驱动电机的转速；nN为驱动电机额定转速；PCu为铜损；Pe为涡流损耗；Ph为磁滞损耗[13]。

图7为车辆空载状态下，踏板开度k=80%时各挡位电机效率曲面，1-2挡电机效率曲面与2-3挡电机效率曲面的交线所对应的车速即为k=80%时的经济性换挡车速，将不同踏板开度与道路坡度下的1-2挡与2-3挡电机效率曲面的交线进行拟合，得到车辆空载、不同坡度条件下的经济性升挡曲面。

图7 车辆空载、k=80%时各挡位电机效率曲面Fig.7 The motor efficiency surface of each gear when the electric vehicle is no-load, k=80%

根据不同道路坡度与车辆载重条件下的换挡约束，对经济性换挡规律进行修正，得到不同道路坡度与车辆载重驾驶条件下的经济性换挡曲面，如图8与图9所示。随着道路坡度与车辆载重的增加，车辆的可换挡区间逐渐减小，随着车辆载重的增加，1-2挡可进行换挡的最大道路坡度由26.06%减小至17.71%，2-3挡可进行换挡的最大道路坡度由15.14%减小至10.82%。

图8 不同驾驶条件下1-2挡升挡曲面(经济性)Fig.8 1-2 shifting surface under different driving conditions(economic)

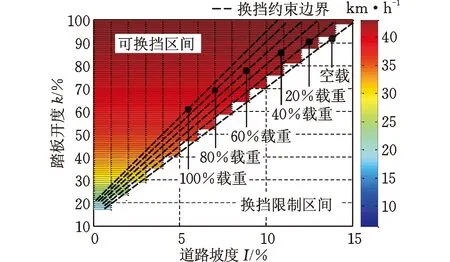
图9 不同驾驶条件下2-3挡升挡曲面(经济性)Fig.9 2-3 shifting surface under different driving conditions(economic)

4 考虑道路坡度与车辆载重的综合性能换挡规律优化

4.1 综合性能换挡规律优化模型

动力性与经济性都是车辆性能的评价指标，但都是以一个性能指标达到最优，牺牲另一个性能指标制定的，由此提出考虑道路坡度与车辆载重的综合性能换挡规律，保证车辆动力性能的同时兼顾经济性能。

4.1.1优化变量

换挡规律是指导车辆在各种驾驶条件下进行换挡，换挡车速的选择会直接影响到车辆的性能，因此选择不同踏板开度、道路坡度与车辆载重条件下的1-2挡换挡车速vs1与2-3挡换挡车速vs2作为优化变量，即

X=(vs1|(k,β,mc),vs2|(k,β,mc))

(5)

4.1.2优化目标

(1)动力性目标。以车辆由静止加速到指定车速的时间ta作为动力性能指标，换挡规律决定了不同挡位驱动车辆行驶的时间，从而影响车辆的加速时间。在不同的道路坡度与车辆载重条件下，车辆能达到的最高车速会随着车辆负载的增加而降低，所以将不同踏板开度下，车辆在不同道路坡度与车辆载重驾驶条件下由静止加速到50 km/h的加速时间作为动力性目标，在车辆无法达到50 km/h车速的驾驶条件下则选择车辆由静止加速到当前最高车速的时间为动力性目标，如下：

(6)

(7)

式中，Ft1、Ft2、Ft3分别为变速系统工作在1挡、2挡、3挡的驱动力；Fb为车辆行驶过程中受到的阻力。

(2)经济性目标。选择不同踏板开度下，车辆在不同道路坡度与车辆载重驾驶条件下由静止加速到当前工况最高车速所需的能耗(kW·h)作为经济性目标，能耗为车辆加速过程中需要的总能耗，即

(8)

式中，tn为车辆运行在第n挡的时间。

4.1.3约束条件

车辆在行驶过程中首先要满足车辆的动力需求，保证车辆在平路及坡道工况下的通过性，同时为避免车辆在坡道工况下发生循环换挡，不可出现车辆在换挡后发生减速的情况，即车辆由第n挡切换为第n+1挡后加速度小于0：

(9)

综合性能换挡规律在满足不同驾驶条件车辆动力性的前提下，还要兼顾车辆行驶过程中的经济性，因此在同一换挡车速下，下一挡位驱动电机的效率应高于上一挡位：

(ηM|in+1>ηM|in)|(k,β,mc)

(10)

同时各驾驶条件下的换挡车速不可超过当前挡位驱动电机可提供的极限转速，即

(11)

4.2 优化模型求解

在综合性能换挡规律优化模型中，优化变量X为连续优化变量。引力搜索算法(GSA)是模仿万有引力定律的启发式优化算法，具有全局搜索能力强、收敛速度快、鲁棒性强的特点，在非线性优化问题中具有良好的性能。分层引力搜索算法(HGSA)在GSA算法的基础上进行了改进，可增强算法的寻优能力，有效避免算法陷入局部最优[14]。HGSA算法中根据质点适应度函数来计算各质点质量，由质量决定各质点对其他质点的引力作用。随着算法迭代次数的增加，各质点在空间中的位置与速度不断变化，使得各质点质量发生变化。质点的适应度越好，质量越大，越接近于最优解。同时算法中引入分层机制，使算法更容易跳出局部最优。分层引力搜索算法的流程图见图10。

图10 分层引力搜索算法优化流程Fig.10 Optimization flow of hierarchical gravitational search algorithm

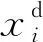
(12)

优化得到的各挡位综合性能换挡规律如图11～图14所示，分析优化结果可看出，在踏板开度一定的情况下，随着道路坡度与车辆载重的增加，各挡位的可换挡区间逐渐减小，各挡位的换挡车速随着道路坡度与车辆载重的增加逐渐提高。车辆空载时可进行1-2挡升挡操作的最大坡度为25.57%，满载时可进行升挡操作的最大坡度为17.21%；车辆空载时可进行2-3挡升挡操作的最大坡度为15.25%，满载时可进行升挡操作的最大坡度为9.83%。同时由于低踏板开度下驱动电机提供的转矩较小，车辆在高负荷工况下无法达到符合换挡约束的车速，故不进行换挡。

图11 车辆空载1-2挡换挡曲面Fig.11 1-2 gear shifting surface under no-load

图12 车辆满载1-2挡换挡曲面Fig.12 1-2 gear shifting surface under full-load

图13 车辆空载2-3挡换挡曲面Fig.13 2-3 gear shifting surface under no-load

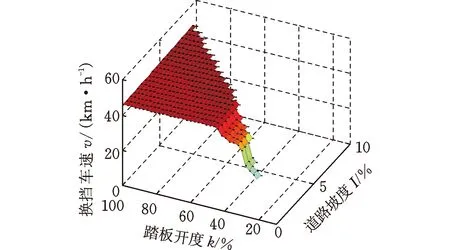
图14 车辆满载2-3挡换挡曲面Fig.14 2-3 gear shifting surface under full-load

5 案例验证与分析

结合整车参数与动力系统参数，基于MATLAB/SIMULINK仿真平台建立整车模型，选择CHTC-LT货车驾驶循环工况，对纯电动三挡物流车行驶过程中的状态进行仿真，将综合性能换挡规律与动力性换挡规律及经济性换挡规律进行对比分析。同时在不同道路坡度与车辆载重的驾驶条件下对车辆进行仿真，分析车辆换挡与车速变化情况，验证综合性能换挡规律对动态驾驶环境的适应性。

5.1 动力性能对比分析

以整车从静止开始加速达到50 km/h所需要的时间作为车辆动力性能的评价指标，通过仿真得到表4所示仿真结果。由表4可看出，随着车辆载重增加，各换挡规律所需加速时间逐渐增长，在各载重条件下经济性能换挡规律与动力性能换挡规律的加速时间差异保持在3.50%～3.66%，综合性能换挡规律与动力性能换挡规律的加速时间差异保持在1.02%～1.16%，综合性能换挡规律表现出良好的动力性能。

表4 动力性能对比

5.2 经济性能对比分析

本文研究的纯电动物流车整车质量为4495 kg，故选定整车在CHTC-LT循环工况下的比能耗作为车辆经济性能评价指标，如图15所示。对各载重条件下的车辆进行仿真，然后对得到的各换挡规律的工况比能耗进行对比分析。

图15 物流车CHTC-LT驾驶循环Fig.15 CHTC-LT driving cycle of commercial vehicle

表5与表6所示分别为各载重工况车辆在CHTC-LT(市区+城郊)与CHTC-LT中(完整工况)的经济性能仿真结果。通过对比仿真结果可得到如下结论：随着车辆载重的增加，动力性换挡规律与经济性换挡规律的比能耗差异逐渐减小。同时由于CHTC-LT(市区+城郊)中车辆启停次数多，车速变化频繁，车辆换挡次数多，各载重状态下的车辆动力性换挡规律与经济性换挡规律的比能耗差异保持在2.92%～3.81%；在CHTC-LT(完整工况)下，由于高速区间部分车辆启停次数少，车速变化频率相对于市区循环部分变化频率较小，在整个CHTC-LT(完整工况)驾驶循环中动力性换挡规律与经济性换挡规律表现出的比能耗差异保持在1.39%～1.77%。

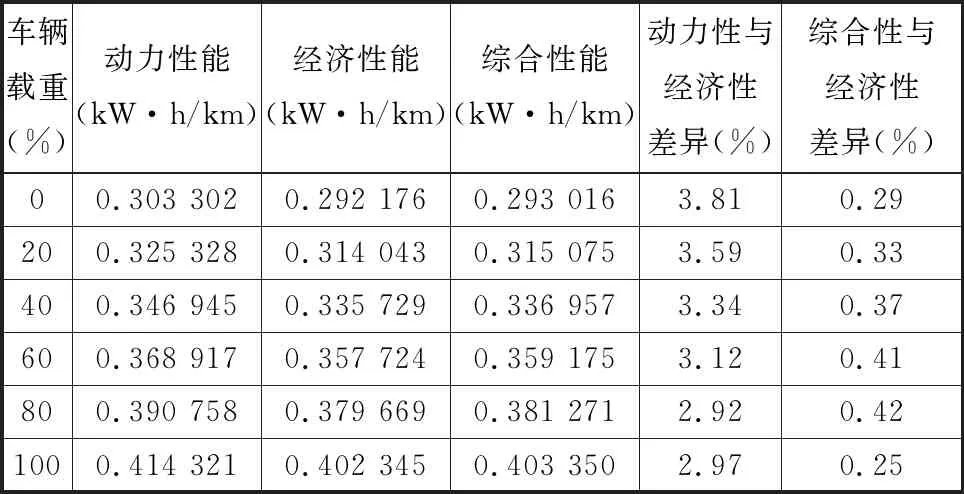
表5 CHTC-LT(市区+城郊)经济性能对比

表6 CHTC-LT(完整工况)经济性能对比

在各车辆载重条件下，综合性能换挡规律与经济性换挡规律在CHTC-LT(市区+城郊)中的比能耗差异为0.25%～0.42%；在CHTC-LT(完整工况)中的比能耗差异为0.16%～0.24%，综合性能换挡规律始终表现出良好的经济性。

5.3 动态适应性对比分析

为验证考虑道路坡度与车辆载重的综合性能换挡规律对动态驾驶环境的适应性，列举出两种驾驶条件，对比车辆行驶过程中静态换挡规律与动态换挡规律的换挡与车速变化情况，降挡速差取值范围为2～8 km/h。

如图16所示，取降挡速差为5 km/h，满载车辆在10%坡度道路上由静止以100%踏板开度开始加速，采用静态换挡规律的车辆在第52 s进行了2-3升挡操作，此时车速为46 km/h，由于3挡提供的驱动力不足以克服车辆受到的行驶阻力，故进行减速，直到车辆减速至41 km/h，车辆进行3-2降挡操作并重新开始加速，由此产生换挡循环，挡位在2-3挡之间不断切换，同时车速不断在41～46 km/h之间波动。

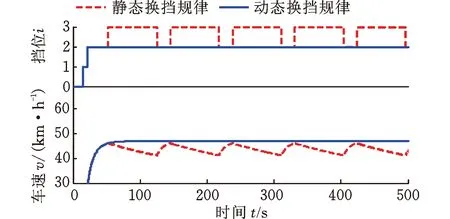
图16 10%坡度-满载-100%踏板开度Fig.16 Gradient 10%-full load-throttle opening 100%

动态换挡规律充分考虑了道路坡度与车辆载重对车辆换挡的影响，在10%道路坡度与100%载重工况下，车辆工作在2挡时不进行升挡操作，始终工作在2挡，受限于驱动电机提供的驱动力大小，车速提升并稳定至48.8 km/h，挡位及车速不发生波动。在8.3%坡度-空载-60%踏板开度(图17)的驾驶条件下，动态综合性能换挡规律相较于静态换挡规律消除了换挡循环现象，提高了车辆对动态驾驶环境的适应性。

图17 8.3%坡度-空载-60%踏板开度Fig.17 Gradient 8.3%-no-load-throttle opening 60%

为探究降挡速差取值大小对换挡循环的影响，在8.3%坡度-空载-60%踏板开度的驾驶条件下，对比降挡速差取2 km/h、5 km/h与8 km/h的换挡循环情况。如图18所示，在降挡速差取值2 km/h时，相较于降挡速差取5 km/h与8 km/h时车辆的换挡更为频繁，车速在44～46 km/h区间内进行变化，相较于降挡速差取5 km/h与8 km/h时速度波动较小，降挡速差取为8 km/h时速度波动最大。由对比分析可知，降挡速差取值较小会导致车辆在换挡循环中的换挡更为频繁，而降挡速差取值过大会导致循环阶段的速度波动较大，波动幅值取决于降挡速差的取值大小。

图18 不同降挡速差下的换挡循环Fig.18 Shift cycle under different downshift speed difference

6 结论

(1)对于纯电动物流车三挡变速系统，同踏板开度下动力性换挡规律的换挡车速会随着道路坡度与车辆载重的增加而提高；经济性换挡规律的换挡车速不随着道路坡度与车辆载重的增加发生变化，但可换挡区间会随之减小；所提出的综合性能换挡规律能较好地兼顾车辆的动力性与经济性，并在不同道路坡度与车辆载重行驶条件下消除换挡循环，适应动态驾驶环境。

(2)基于MATLAB/SIMULINK平台对不同取值条件下的综合性能换挡规律进行仿真分析发现，降挡速差取值越小，车辆在换挡循环阶段的换挡越频繁，并且，车辆在换挡循环阶段的速度波动取决于降挡速差大小。

(3)文中主要研究了考虑道路坡度与车辆载重的纯电动三挡物流车综合性能换挡规律，而变速器在换挡过程中存在着换挡冲击与转矩波动等问题，对车辆的性能也有着重要影响，因此，在制定换挡规律时结合变速器的换挡品质分析，使车辆获得更好的性能是下一步的研究重点。