波形弹簧的失效分析与改进设计
2021-02-22金胜秋蒋哲昊
金胜秋 蒋哲昊 叶 超
博西华电器(江苏)有限公司 南京 210046
1 研究背景
传动系统是滚筒洗衣机的重要组成部分,轴承是传动系统的关键零件。通过对轴承施加一定的轴向力来调节轴承工作游隙,保证轴承工作稳定性,是行业内的普遍做法[1-3]。波形弹簧是负责向轴承施加轴向力的常见弹性元件,具有安装空间小、弹力调控好等优点。然而,波形弹簧若出现磨损甚至开裂,则无法按照设计意图实现轴承工作性能优化,甚至还会给系统带来额外的负载,对轴承工作性能造成破坏[4]。由此可见,对波形弹簧在试验中出现的磨损及失效现象进行深入分析,并进行改进设计,是非常有必要的。
2 失效现象
用于为洗衣机轴承提供轴向力的波形弹簧在寿命试验中发生不同程度的断裂和磨损,如图1所示。由于波形弹簧双侧接触点有明显的摩擦痕迹,因此观察与波形弹簧接触的零部件形貌,如图2所示。由图2可以看出,轴承内圈及皮带轮端面都出现了明显的环形摩擦痕迹,进一步表明波形弹簧在工作过程中出现了相对转动。

▲图1 波形弹簧磨损
波形弹簧在工作过程中受力情况比较复杂,伴随断裂同时产生的还有材料磨损现象,单一通过观察失效现象很难判断导致失效的根本原因,需要进行进一步分析。
3 断口分析
在显微镜下对波形弹簧断口形貌进行观察,如图3所示。由图3可以看出,开裂起点位于有摩擦痕迹的一侧,说明摩擦造成的材料损失削弱了材料的抗疲劳能力。断口上存在疲劳裂纹扩展区E和瞬时断裂区M,疲劳裂纹扩展区明显比瞬时断裂区大,表明波形弹簧在应力作用下发生疲劳断裂[5]。

▲图2 波形弹簧关联零部件形貌▲图3 波形弹簧断口形貌
4 微观结构与硬度分析
使用硬度测试仪对波形弹簧裂纹两侧进行硬度检测,断口区硬度分布较为稳定,维氏硬度约为506,符合设计要求。此外,在显微镜下观察波形弹簧断裂区域的微观结构,如图4所示。断裂区域微观结构均匀,表明没有热处理不良[6]。

▲图4 波形弹簧断裂区域微观结构
综合以上分析,导致波形弹簧开裂的两个重要因素是波形弹簧磨损和动态应力作用。失效样品中有一部分只有磨损,没有开裂,表明波形弹簧磨损先于开裂发生。由此可知,波形弹簧失效过程为:波形弹簧发生相对转动产生磨损,强度被削弱,在动态应力作用下,发生开裂。
5 磨损原因分析
波形弹簧先产生磨损,然后在应力作用下产生疲劳开裂。波形弹簧发生相对转动产生磨损与受力情况相关,简化波形弹簧的受力,如图5所示。波形弹簧分别与皮带轮和轴承内圈端面相接触,接触点为A和B。在外力Fs的作用下,波形弹簧压缩变形量为δ,对应产生反抗压力Ns,即预紧力。作用力在波形弹簧与轴承及皮带轮之间均为摩擦传递,因此,影响摩擦力大小的波形弹簧预紧力是关键因素。
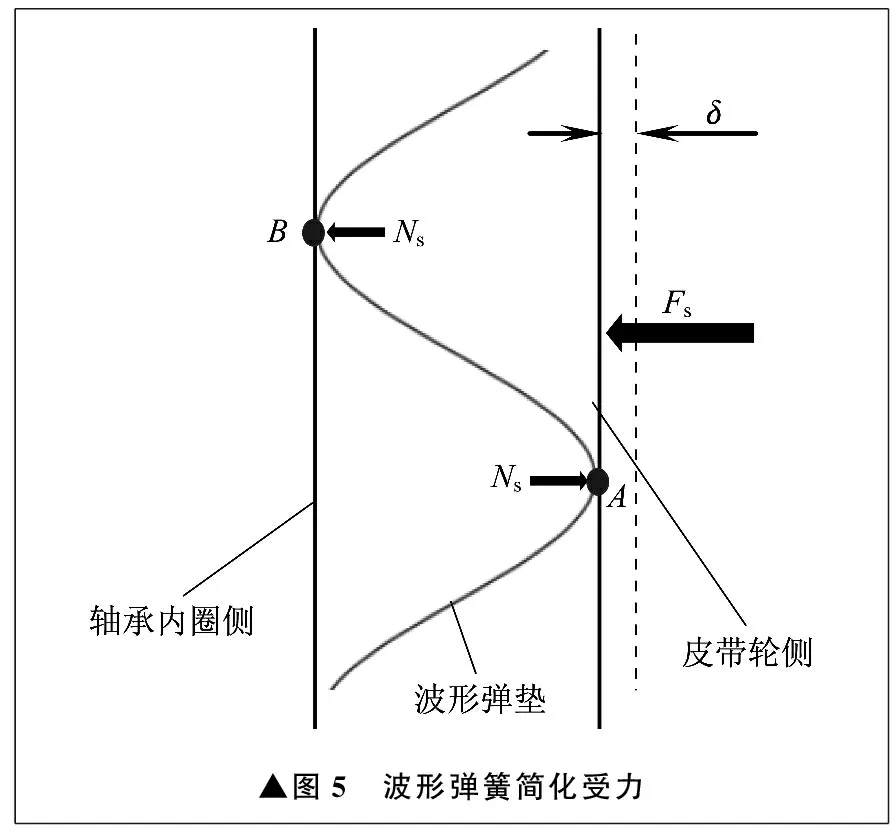
▲图5 波形弹簧简化受力
5.1 预紧力要求
波形弹簧在洗衣机中位于轴承与皮带轮之间,波形弹簧在正常装配状态时被压缩δ,产生预紧力Ns。对于皮带轮、轴承、波形弹簧三者之间的关系,设计意图是当皮带轮在皮带带动下开始转动时,三者同步转动,不允许发生相对转动,避免产生磨损。为了确保设计意图可以实现,需要满足以下关系式:
(1)
式中:μA为波形弹簧与皮带轮之间的摩擦因数;μB为波形弹簧与轴承内圈端面之间的摩擦因数;Fz为波形弹簧与轴承内圈及皮带轮同步转动所需要克服的最大阻力;fs为安全因数。
考虑到波形弹簧、轴承内圈、皮带轮均为金属材质,选取μA、μB为0.15。三者共同转动的阻力主要来源于轴承内部的摩擦力,当轴承承受最大径向载荷时,内部摩擦力最大。经过实测,得到某型号轴承在限定径向载荷作用下内部产生的最大摩擦阻力约为500 N。由于阻力值通过实测得到,并且轴承是精密零部件,因此取安全因数fs为1.1。各参数代入式(1),得:
Ns>550 N
5.2 预紧力限制
当波形弹簧的压缩量一定时,预紧力由刚度决定,材料性能及波形弹簧几何形状都是影响刚度的重要因素。由于波形弹簧具有对称性,取波形弹簧的半个波形为分析对象[7],受力如图6所示。由图6可以看出,当受到正向压力时,A点与B点分别承受大小相等方向相反的作用力FA和FB,对两点受力沿水平和垂直方向分解,可得Fax、Fay、Fbx、Fby,关系式为:
(2)
(3)
FB=σA1
(4)
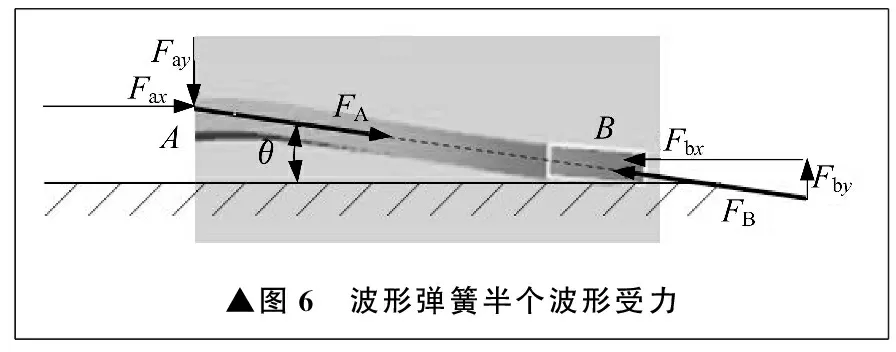
▲图6 波形弹簧半个波形受力
式中:σ为波形弹簧内应力;A1为波形弹簧受力方向上的截面积;θ为波形弹簧被压缩δ时与接触面形成的波形角度;m为波形弹簧模数,即完整波形的数量。
由式(2)~式(4),可得:
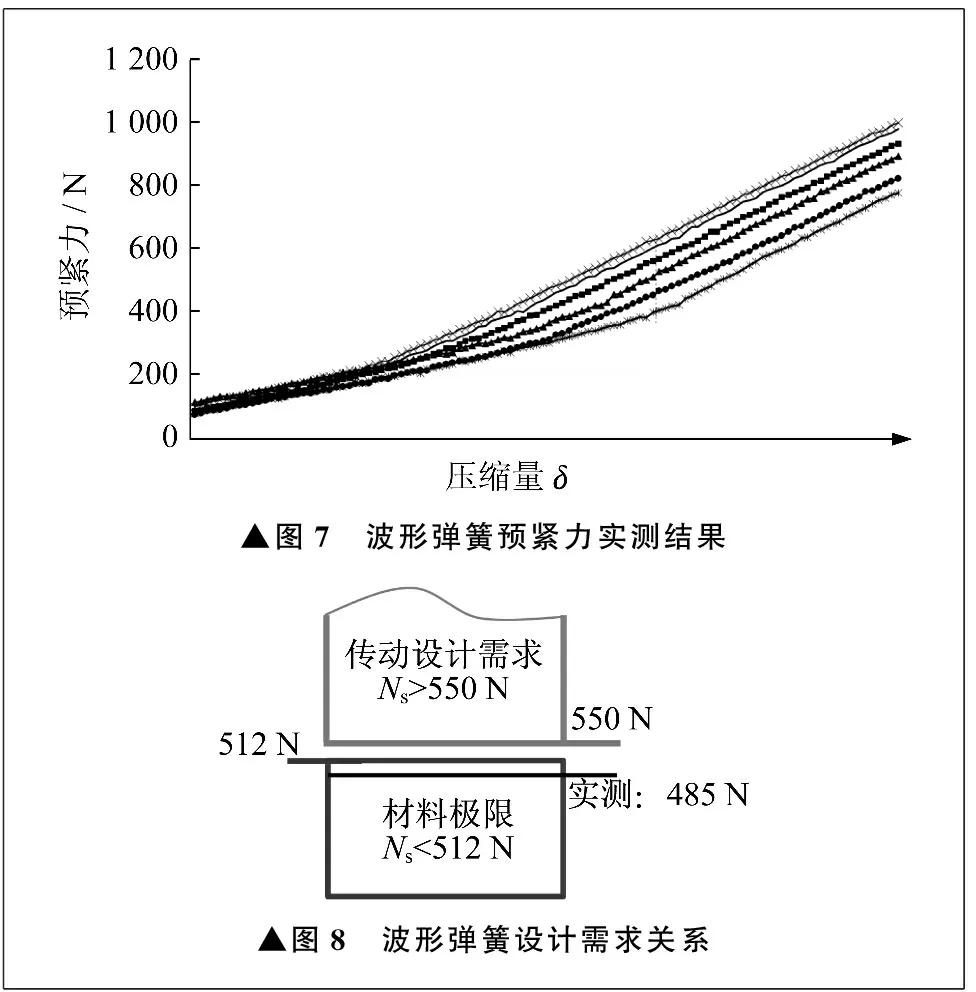
Ns=mσA1sinθ (5) 式中:[σ]为材料许用应力。 将设计参数代入式(5),计算得: Ns<512 N 根据式(5),容易发现波形弹簧的模数m、截面积A1、波形角度θ,以及材料的许用应力[σ]都对波形弹簧预紧力有直接影响。受波形弹簧材料性能和几何形状影响,波形弹簧在弹性工作区工作时的预紧力上限为512 N,小于传动设计所需的550 N。可见,波形弹簧有在塑性变形区域工作的风险。因此,需要对波形弹簧的几何形状进行改进设计,以确保波形弹簧能够在弹性变形区工作。 取六件波形弹簧样品,使用压力试验机对波形弹簧进行预紧力实测,均值约为485 N,实测结果如图7所示。波形弹簧设计需求关系如图8所示。 ▲图7 波形弹簧预紧力实测结果▲图8 波形弹簧设计需求关系 实测结果表明,波形弹簧样品的预紧力趋势比较一致,但个体性能有差异。当波形弹簧被压缩,预紧力小于材料许用值(512 N)时,波形弹簧在工作过程中不会发生塑性变形。但是由于预紧力未能满足传动系统对预紧力的需求,因此波形弹簧与轴承内圈、皮带轮之间产生的摩擦力不足以克服系统阻力,使波形弹簧发生相对转动,产生磨损。当波形弹簧被压缩,预紧力大于材料许用值(512 N)且小于传动系统需求(550 N)时,波形弹簧有发生塑性变形的风险,同时也无法满足传动系统对预紧力的需求,因此同样会发生相对转动,产生磨损。当波形弹簧被压缩,预紧力大于传动系统需求(550 N)时,波形弹簧会发生塑性变形,导致预紧力损失,最终也会在工作中发生相对转动,产生磨损。 综合以上分析可知,波形弹簧在工作中与轴承和皮带轮之间会发生相对转动,并产生磨损,必须对波形弹簧进行改进设计。 对波形弹簧进行改进设计主要集中在两个方面。一方面是当前波形弹簧设计中,材料能承受的极限应力尚不能满足传动设计需求,需要进行改进。根据式(5)可知,波形弹簧的模数m、截面积A1,以及波形弹簧波形与水平面波形的夹角θ对波形弹簧预紧力有影响,可从上述参数入手考虑改进方案。另一方面,提高波形弹簧的刚度,在压缩量不变的条件下,提高预紧力,进而满足传动设计需求。对波形弹簧刚度进行提高需要基于波形弹簧刚度计算式。波形弹簧需满足如下设计要求: 550 N (6) 波形弹簧预紧力为: Ns=kδ (7) 可见,当波形弹簧压缩设计值不变时,需要通过提高波形弹簧刚度来提高预紧力。根据JB/T 13296—2017《波形弹簧 技术条件》[8],波形弹簧刚度k为: (8) b=(D2-D1)/2 (9) D=(D2+D1)/2 (10) 式中:E为弹簧材料的弹性模量;b为波形弹簧宽度;D为波形弹簧中径;D2为波形弹簧外径;D1为波形弹簧内径;K为模数对应的刚度修正因数,可根据表1查得;t为波形弹簧厚度。 表1 波形弹簧刚度修正因数 式(8)可整理为: (11) 取三款不同设计的波形弹簧数据来验证式(11)的精度,三款波形弹簧模数均为4,弹性模量均为212 GPa,刚度修正因数均为3.88。三款波形弹簧预紧力理论计算值与实测值对比如图9所示,平均误差率约为3.1%,计算精度可以接受。可见,式(11)可以用于波形弹簧的刚度设计。 ▲图9 波形弹簧预紧力理论计算值与实测值对比 观察式(11)可知,影响波形弹簧刚度的主要因素有模数、厚度、刚度修正因数、中径、宽度。其中,刚度修正因数仅受到模数影响,因此不单独进行分析。应用MATLAB软件对式(11)进行因子影响分析,分析结果如图10~图13所示。由图10~图13可以看出,模数、厚度、宽度对波形弹簧刚度的影响是正向的,而中径对波形弹簧刚度的影响是负向的[9]。 通过观察图10~图13的刚度数量级可知,波形弹簧刚度对模数及厚度的变化较为敏感,对中径及宽度的敏感度则略低。随着模数的增加,厚度对波形弹簧刚度的影响逐步加重。随着厚度的增大,模数对波形弹簧刚度的影响也逐步加重,两者互相增益。随着宽度的增大,中径对波形弹簧刚度的影响也逐步加重。随着中径的增大,宽度对波形弹簧刚度的影响则呈现减弱趋势。 ▲图10 模数对波形弹簧刚度影响▲图11 厚度对波形弹簧刚度影响▲图12 宽度对波形弹簧刚度影响▲图13 中径对波形弹簧刚度影响 基于影响因子分析结果,考虑当前波形弹簧刚度水平与目标值差距不大,决定以宽度为切入点改进设计。宽度的变化也会带来中径的变化,为了降低波形弹簧变化对已有系统中其余零部件的影响,采取保持波形弹簧内圈直径不变,增大外圈直径的策略[10]。宽度还是组成波形弹簧截面积的因子之一,增大宽度还可以提高波形弹簧的力学性能。 根据图12、图13可以找到数个满足需求的解,结合工程实际,选择最佳方案。最佳方案中波形弹簧外径为36.5 mm。改进设计前后波形弹簧预紧力对比见表2。改进设计后,波形弹簧在弹性工作区工作,并且能够满足传动设计需求。 表2 波形弹簧预紧力对比 笔者分别从材料和力学角度对波形弹簧进行失效分析,在此基础上确认失效的根本原因,并进行改进设计。 对开裂波形弹簧及其关联零部件进行失效形貌分析,结合显微镜观察失效波形弹簧断口形貌、微观结构,进行硬度测定,确定波形弹簧发生开裂的原因是磨损造成材料损失,动态应力作用下产生疲劳断裂。 对波形弹簧进行力学分析,得到波形弹簧预紧力的设计边界条件,确定导致波形弹簧产生磨损的根本原因是预紧力设计不足,同时发现波形弹簧当前设计无法同时满足技术需求与机械性能要求。 对波形弹簧刚度计算式进行理论与实测对比,计算误差约为3.1%,精度可以接受。通过对刚度影响因子进行分析,确认波形弹簧的模数、厚度、宽度对波形弹簧刚度有正向影响,中径对波形弹簧刚度有反向影响,其中,模数和厚度对刚度影响较大,中径和宽度对刚度影响较小。模数和厚度两者互为增益,任意一项改变都能改变另一项对刚度的影响程度。 笔者对波形弹簧的失效分析与改进设计具有参考价值。需要注意的是,笔者引用的波形弹簧刚度计算式有应用范围,在进行分析时需确认是否适用。5.3 预紧力测定
6 改进设计
6.1 改进概述
6.2 波形弹簧刚度计算


6.3 刚度影响因子分析
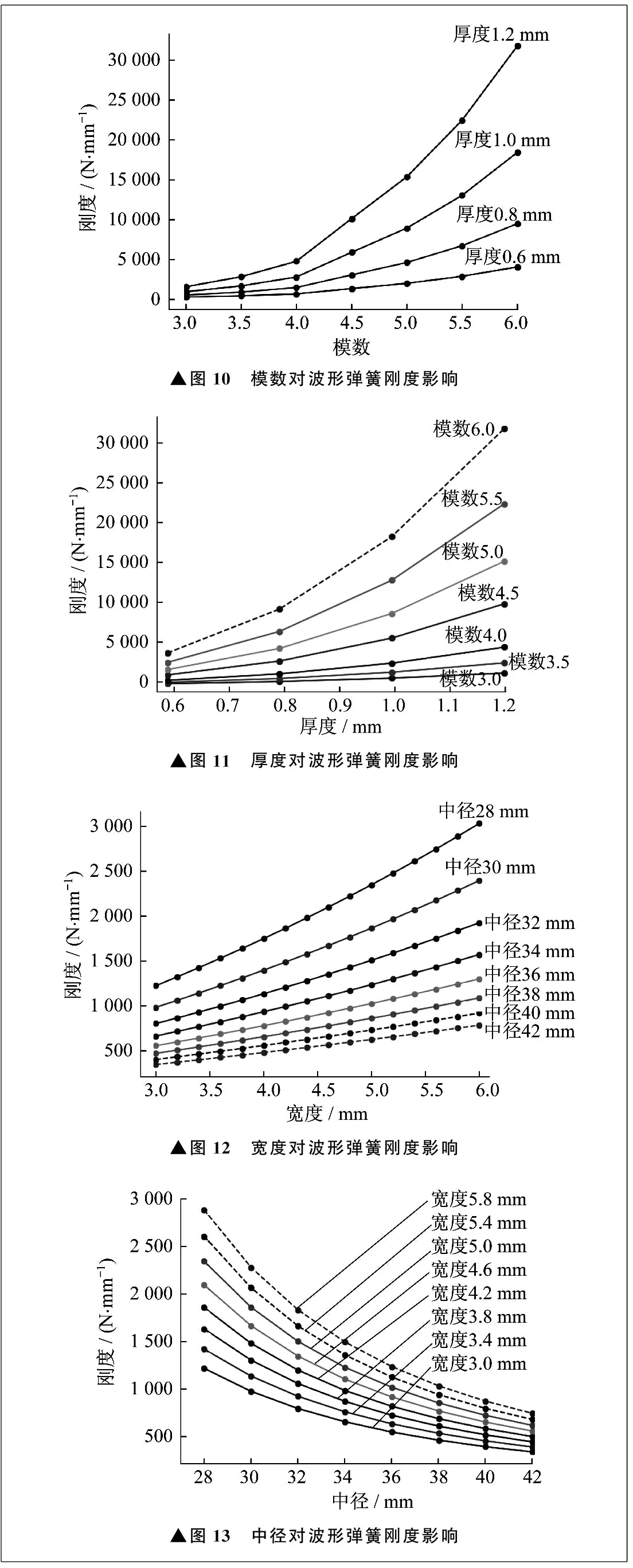
6.4 改进结果

7 结束语
