实时混合模拟中偶发计算延迟的产生及影响

黄 亮 黄慎江 王静峰 徐伟杰 郭 彤

(1合肥工业大学土木与水利工程学院，合肥 230009)(2合肥工业大学土木工程结构与材料安徽省重点实验室，合肥 230009)(3东南大学混凝土及预应力混凝土结构教育部重点试验室，南京 211189)

抗震试验是检验土木工程领域新理论、新结构和新材料有效性的重要手段，也为抗震设计提供了重要的实践支撑[1].由Nakashima等[2]提出的实时混合模拟试验是一种在有限空间内进行大尺度动力试验的有效方法.该方法继承了拟动力试验思路，采用子结构交互技术，实现了有限元计算分析和动力加载试验的同步交互耦合，可同时反映整体结构抗震性能和局部构件的变形损伤，是今后土木工程实验的发展方向之一.

实时混合模拟对实验的软硬件设备要求较高.硬件方面更新了高性能计算机、高速信息通讯设备及动态加载控制系统；软件方面开发了新的积分算法和误差修正方法[3].上述技术革新使得该试验方法具有在真实时间尺度内同步计算、同步加载、同步信息交互的能力.

实时混合模拟要求子结构间的信息同步交互.然而，积分计算延迟、数字/模拟信号转换、数据通讯、控制器采样频率和液压作动器动力响应延迟等[4]均会导致子结构间信息交互不同步.其中，积分计算延迟和液压作动器响应延迟分别是导致数值子结构有限元分析和试验子结构动力加载延迟的最主要原因，其余延迟极小，可忽略不计.

积分计算和作动器响应延迟对实时混合模拟试验的影响截然不同.前者会导致试验停顿，破坏试验的连续性；后者则会影响试验结果的准确性和试验系统的稳定性.目前的研究大多关注作动器延迟的影响评估、时滞误差控制和补偿方法等[5-7].

本文研究了积分计算延迟的产生机理和影响，提出减少计算延迟的方案，并采用试验加以验证.

1 实时混合模拟试验

1.1 基本原理

实时混合模拟试验将整体结构视为研究对象，并划分为数值与试验子结构2个部分.参考文献[8]，试验步骤如下：

① 划分数值与试验子结构，建立运动方程

(1)

② 选择积分算法，求解运动方程，获得第i+1步位移ui+1.

为了保证试验的实时性，要求每一步试验的执行时间等于该步的积分步长.

1.2 积分算法和子步技术

MTS公司提供的实时混合模拟解决方案中，数值子结构采用有限元软件OpenSees进行分析，并提供Newmark[9-10]、HHT-α[11]、Generalized-α[12]和TRBDF2[13]等积分算法用于数值积分.为了兼顾算法精度和稳定性，推荐使用隐式Generalized-α算法通过Newton迭代求解运动方程.一旦残差收敛到阈值，便可获得第i+1步动力响应.为了平衡计算效率和准确性，积分步长Δt通常取控制步长δt的整数倍，且不超过0.02 s，残差阈值通常取10-6～10-4.

上述方案中，计算耗时与残差阈值相关.阈值越小，隐式算法的收敛速度越慢，计算耗时越长.然而，实时试验对同步性要求较高，不允许出现因计算延迟所导致的试验停顿现象.因此，方案中引入了预测-修正子步技术，用于增大积分步长，延长计算时间.子步技术缓解了计算资源紧张的压力，但无法彻底解决计算延迟问题.

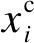
图1 预测-修正过程

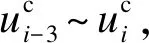
(2)

(3)

式中

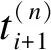
上述预测-修正过程可满足绝大多数计算和加载的需求，但在某些时刻，隐式算法收敛速度缓慢导致计算耗时超限.当控制系统在0.6Δt内仍无法获得下一步指令时，预测-修正模块被迫进入等待阶段，直至计算机完成积分计算，才重新进入修正状态.这一特殊过程即为预测-等待-修正过程.

2 滑移支座试验

本节以在东南大学混凝土及预应力混凝土结构教育部重点实验室完成的滑移支座实时混合模拟试验为例，研究试验中偶发计算延迟产生的原因及影响.

东晋医学家葛洪就曾写过一本医书《肘后备急方》，书名的“肘后”一词，就是说这本书可以放在肘后的口袋中随身携带。“袖珍”一词也是来源于此。而我们常用来比喻官员作风清廉的“两袖清风”，其实原意就是说这个官员袖子里没有装钱。

2.1 试验

滑移支座实时混合模拟试验[15]研究了含新型滑移支座与铅芯橡胶支座的混合隔震体系对4层钢筋混凝土框架的隔震作用(见图2).图中，B柱下的滑移支座分割为试验子结构，其余支座和上部框架定义为数值子结构.梁柱均采用杆件单元进行有限元建模，数值子结构共包含20个节点，56个自由度，仅底部4个节点约束了转动自由度，其余16个节点均包含水平、垂直和转动自由度.

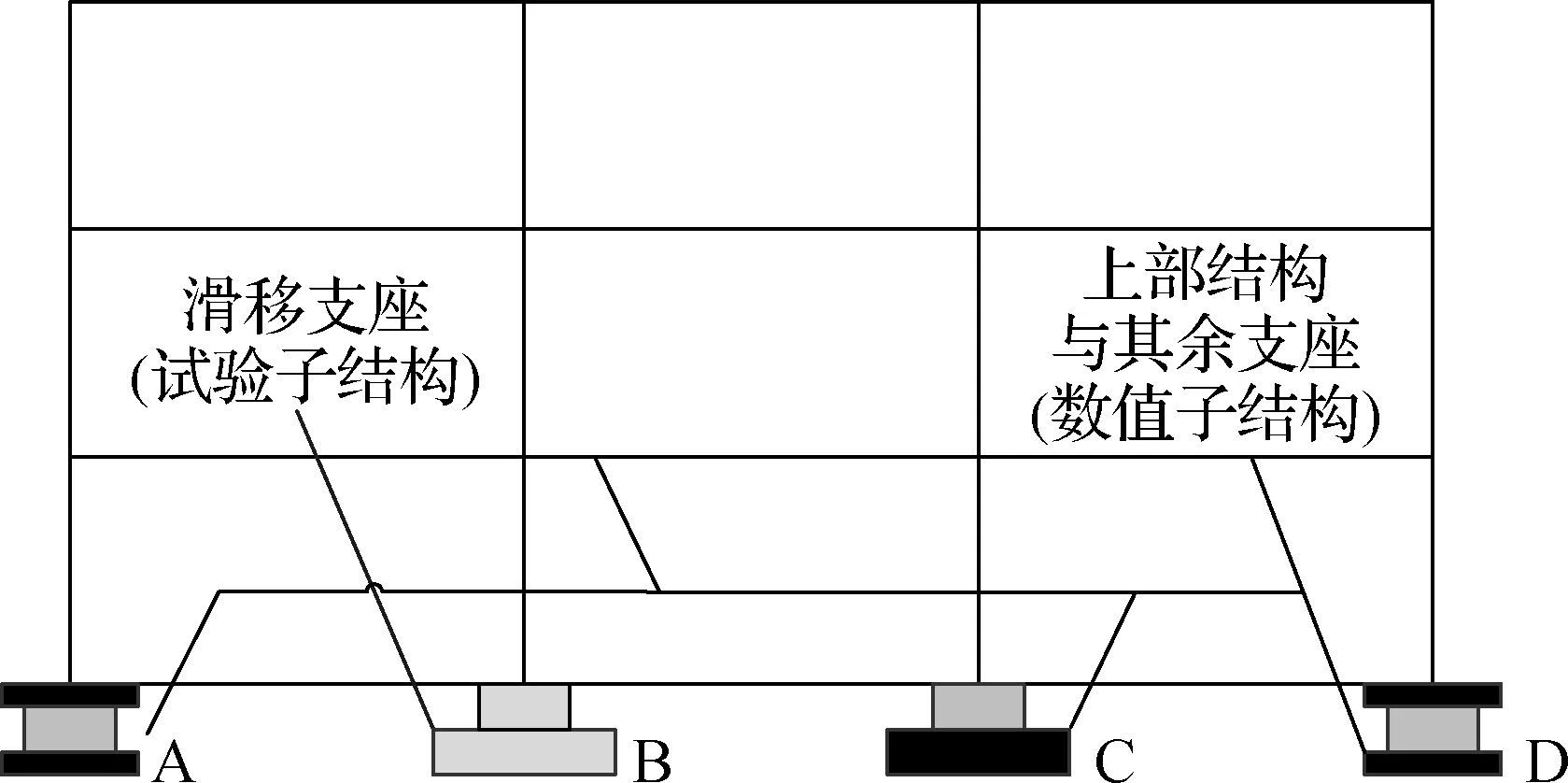
(a) 基础隔震结构示意图

(b) 试验装置照片

试验使用的计算机核心设备包括Intel Core i5-680 3.6 GHz 芯片和2 048 MB 内存.数据采集设备包括8通道数据采集器，采样频率为1 024 Hz.试验系统采用Simulink平台进行流程控制，通过闭环控制系统指挥作动器工作.

试验共完成了El-Centro、Taft和Nanjing地震波作用下各5组实时混合模拟，试验时长分别为60、60和20 s.

2.2 结果分析

经15组重复试验(编号分别为EL-1～EL-5、Taft-1～Taft-5和NJ-1～NJ-5)，发现其中9组试验实现了完全实时同步，其余6组试验出现计算延迟(见表1).统计结果显示，计算延迟具有偶发性和随机性.最严重的计算延迟出现在EL-2的第1 044步，共超时55δt；最轻微的计算延迟出现在Taft-2的第806步，计算超时仅δt.试验时间尺度(即真实耗时与理想耗时的比值)均小于1.001.本文重点分析Taft-3.

表1 计算延迟统计

Taft-3的理想试验耗时为60 s，实际超时71.3 ms，时间尺度为1.001.试验中存在4处短暂停顿，分别在第131、1 768、1 869和2 483步，实际耗时分别为41δt、48δt、35δt和29δt.图3显示了第131步的试验停顿现象.

(a) 计算延迟现象

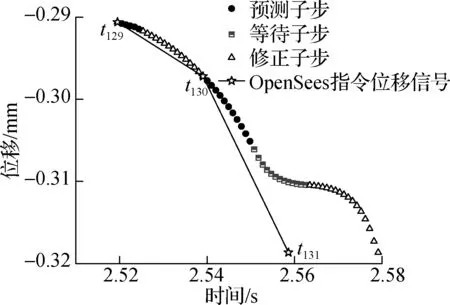
(b) 第131步细节图

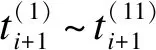
(4)

式中

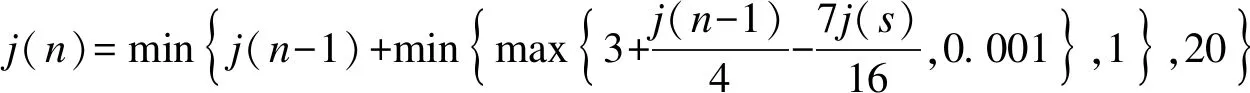
(5)

式中

3 计算延时的影响

计算延迟会对指令位移信号和作动器响应产生影响.

3.1 指令位移信号的影响

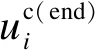
3.2 作动器响应的影响

受液压伺服系统加载误差影响，测量反馈力不仅与终点状态有关，还与加载过程密切相关.

Zhao等[16]对作动器位移追踪进行扫频试验，发现位移追踪效果与指令信号相关，信号频率越高，位移追踪效果越差.出现计算延迟时，指令位移信号呈S形，导致信号中含有高频成分.由于作动

图4 不同计算耗时情况下和

器在短时间内被命令先减速等待再加速追赶，动力加载系统需克服管道内液压油、作动器加载头、试验构件等惯性力作用，使得作动器追踪出现显著误差.因此，S形指令位移信号对位移追踪效果极为不利.

图5(a)～(b)比较了Taft-3试验中t1 766～t1 769与t1 533～t1 536时步的位移追踪效果.由图5(a)可知，t1 766～t1 769时步的位移追踪延迟分别为0、-1、7.8、0 ms，其中负值表示该时步位移过补偿.对于计算延迟出现的t1 768步，由于作动器被命令在48δt内先减速再加速，导致该时步的位移追踪延迟从-1 ms急剧增加到7.8 ms，出现了8.8 ms的响应延迟，表明该时步作动器位移追踪效果极差.由图5(b)可知，t1 533～t1 536时步的位移追踪延迟分别为1.9、2.3、2.2、1.5 ms，未出现计算延迟，故作动器位移追踪效果较好且波动很小.对比发现，由于液压作动器在短时间内被要求急停急转，其响应会出现较大延迟，位移追踪效果也大大降低.因此，需彻底避免计算延迟，防止作动器出现急停急转的现象.

4 克服计算延迟的改进方案

为了防止偶发计算延迟、保障试验的实时性和连续性，可通过使用显式积分算法和简化数值子结构模型提高计算效率，降低计算耗时.

(a) 计算延迟步响应

(b) 标准步响应

降低计算耗时的最有效方法是引入显式积分算法，用于代替需迭代计算的隐式积分算法.实时混合试验中常用的显式算法包括CR算法[17]、Chang算法[18]等.显式积分算法通过递推直接求解运动方程，计算时间可控，大幅降低了积分计算时间.

其次，简化数值子结构模型同样可减少计算耗时.通过模型简化可减少计算自由度，减少非线性单元数量，降低运动方程复杂度，进而减少计算耗时.

上述改进方案已在铅芯橡胶支座实时混合模拟试验[19]中得到验证.该试验采用相同的硬件设备，研究了二层钢框架隔振结构的隔震性能和支座的变形、耗能能力.试验中，梁柱均采用线弹性杆件单元建模，数值子结构仅保留楼板处3个水平自由度，积分算法采用CR显式积分算法.选用EL-Centro地震波进行了12次重复试验，每次试验时长60 s，未发现计算延迟现象，所有试验均保证严格实时同步.该试验验证了使用显式积分算法和简化数值子结构模型可有效降低计算耗时，避免出现由计算延迟导致的实时试验停顿现象.

5 结论

1) 在实时混合模拟中使用隐式积分算法时，试验可能出现偶发计算延迟，该现象具有偶然性和随机性，无法预先补偿.

2) 计算延迟产生的原因是隐式积分算法通过迭代计算求解运动方程，其残差收敛速度缓慢.

3) 计算延迟的影响是使作动器在短时间内急停急转，导致其位移追踪效果大大降低.

4) 通过使用显式积分算法、简化模型等方法可避免出现计算延迟.