“慢”教育视角下的数学课堂教学策略研究①

李现勇

(青岛市教育科学研究院 266001)

著名数学家丘成桐说过：“学数学不要求快，一定要学慢学细”.数学学科的特点，决定了数学教学绝不可片面地追求速度.但在一线教学中，仍存在着“提问多，启发少；节奏快，思考少；容量大，内涵少；指定多，探究少”等一系列问题，教师一味地追求教学速度与进度，将知识全盘托出，甚至填鸭式教学，导致学生对知识一知半解，对公式、定理的掌握仅仅停留在记忆与应用的层面上.如此一来，学生只是被动接受，没有思维的锻炼与能力的提升，这与数学教育的初衷背道而驰，因此，实施“慢”教育，对改善学生思维现状、提升学生学科素养具有重要意义.

“慢”教育，并非指单纯拖延教学进度、降低课堂效率、减少课堂容量的“慢”，而是追求与学生身心发展同步，关注学生“最近发展区”的“慢”.“慢”教育主张给学生充分的“想”和“悟”的时间，本质上来说，就是要充分发挥学生的主体作用，让他们充分体验、深入理解、透彻领会，从而真正掌握数学的精髓与真谛.那么，数学课堂的“慢”，具体体现在哪些环节呢？以下将结合具体案例，从三个方面展开论述.

1 “慢”在概念形成

概念教学是数学教学的核心内容.数学概念的形成过程要求学生将已有知识外延，构建新的知识，蕴含着丰富的数学思想.因此，实施“慢”教育，先从概念形成过程开始.数学概念的“慢”教学，要讲清概念的来龙去脉，要循序渐进地进行引入.

如，对于函数极值的概念，设计这样引入：

提出问题在用导数研究函数的单调性时，我们发现利用导数的正负可以判断函数的增减.如果函数在某些点处的导数为0，那么在这些点处函数有什么性质呢？

思考观察下图，我们发现，当t=a时，高台跳水运动员距水面的高度最大.那么，函数h(t)在此点的导数是多少呢？此点附近的图象有什么特点？相应地，导数的正负性有什么变化规律？

探究如下图，函数y=f(x)在x=a,b,c,d,e等点的函数值与这些点附近的函数值有什么关系？y=f(x)在这些点的导数值是多少？在这些点附近，y=f(x)的导数的正负性有什么规律？

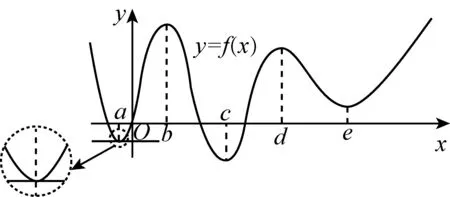
在实际教学中，教师可以从单调性与导数值正负的关系进行引入，“我们已经研究了导数值为正或负时分别对应的函数单调性情况”，接着自然而然地抛出问题：“那么，当导数为0时，函数性质又是怎样的？”学生首先联系前面所学，“利用导数的正负可以判断函数的增减”，引发思考：“若某点的导数为0，则函数在这一点处有何性质”.学生就会结合导数为0的条件，在脑海中想象出对应的函数图象，或想到熟悉的、符合条件的函数解析式，而在这个过程中便产生了形与数的结合，是对学生直观想象能力和数学抽象能力的一种培养与锻炼.

接下来，教师设计从具体实例——跳水模型入手，描绘出跳水运动员跳水过程中的运动曲线，引导学生思考函数在最高点处的导数值、该点附近的图象特点等一系列问题.接下来，由一个极大值点拓展到若干个极大(小)值点：给出特殊函数y=f(x)的图象，引导学生探究在各个极大(小)值点处的导数值、附近导数的正负、函数图象等一系列特点，由此最终得出函数极值的概念.

上述过程中，学生经历从实际问题中抽象出数学模型，由已知到未知，由具体到抽象，由特殊到一般，自然而然地归纳出函数极值的概念.而这样的“慢形成”方法，使学生在获得极值概念的同时，还发展了数学抽象、直观想象、逻辑推理等数学核心素养.

不仅是数学概念的教学，对于定理和法则同样如此.对于概念、定理和法则，它们从何而来？因何而起？具有怎样的数学背景和数学意义，蕴含怎样的数学文化和应用价值？“慢形成”教学，要求给学生足够的思维时空，让学生经历数学概念的抽象过程和定理的证明过程，通过研读教材、巧妙设计来引导学生追溯数学家的思维方式，发现问题研究的源头.

2 “慢”在问题探究

教师是课堂的主导，而学生是课堂的主体.在面临问题解决时，教师应把课堂更多地交给学生，由“传授型”课堂转变为“探究型”课堂；而在设计探究性课堂时, 要求教师不仅要关注所探究的问题是否符合数学学科特点，更要关注是否符合学生发展需要[1].因此，在探究过程中所设计的问题，务必是精心设计的、有层次感的，不能是碎片化的.通过剥茧抽丝、逐层深入的问题串，将知识进行有效的串联，为学生提供思维方向的指引，从而引发学生递进式、多角度的思考.问题串的设置，使整个课堂慢下来，在“慢探究”中，充分发挥学生的主体性与自主性，使其亲身经历探究与归纳的过程，从而加深对问题的理解，丰富自身的学习感悟与体验.

如，在函数概念的引入中，可以依据教材，设置如下问题串：

情境一：某“复兴号”高速列车加速到350km/h后保持匀速运行半小时.列车行进的路程为S(单位：km)，运行时间t(单位：h).

问题1：这段时间内，列车行进路程S与运行时间t的关系可以表示为？

问题2：列车行进路程S是运行时间t的函数吗？

情境二：下图是北京市2016年11月23日的空气质量指数(Air Quality Index，简称AQI)变化图.

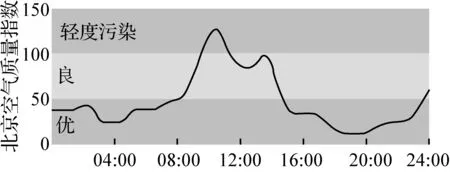
问题3：如何根据该图确定这一天内任一时刻th的空气质量指数(AQI)的值I？

问题4：你认为这里的I是t的函数吗？

问题5：上述情境1和情境2中的函数都有哪些共同特征？你能用文字语言归纳并概括一下吗？

问题6：如何根据以上共同特征，用符号语言给出函数的定义？

问题7：你能举一些我们学过的函数的例子吗？

情境一中，问题1引导学生观察行进路程与时间之间的关系，并给出关系式.从实际问题中抽象出数学问题，本质上就是数学建模的过程，问题1的设置使学生对问题形成初步的感知，培养了学生数学建模的思维和能力；问题2使学生思考初中所学的函数定义，进一步感知变量间的关系，为函数概念的得出奠定基础.情境二中的问题3和问题4，则以曲线图的方式呈现，使学生从另外的角度感知变量关系.问题5和问题6则通过引导学生观察猜想、归纳概括，使其发现函数的本质特征，经由口头表述、文字语言表达，最终凝练成符号语言，这一过程锻炼了学生的归纳推理能力、语言表达能力和总结概括能力，同时训练了数学抽象、逻辑推理的学科素养.用符号语言表达的函数定义毕竟是抽象的，有的学生不容易理解，而问题7的设置使学生列举自己学过的函数，对函数定义进行验证，如此一来，使抽象概念具体化，有利于加快学生对函数概念的理解和消化.

“慢探究”课堂是归纳和体验的交融与统一.学生通过不断地经历观察、归纳和体验的过程，可以多角度、全方位地辨析概念，形成对概念更全面、更立体的理解与认识.在教学中，教师应当创设有深度、有层次的问题，激发学生的探究欲望，鼓励其积极思考、自主学习，从而加深对知识的认识，提高直观想象、数学抽象、逻辑推理等核心素养.

3 “慢”在交流碰撞

教师鼓励学生自主探究和合作探究，要给学生留出充裕的思考时间和交流时间，“慢交流”通过师生对话、生生对话等使学生经历知识的融汇、碰撞与整合，最终形成自己的想法，获得对问题的思考与解答.

如，在立体几何部分棱柱概念的教学中，棱柱的定义是“有两个面互相平行，其余各面都是四边形，并且相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱”.此时教师抛出问题，“‘相邻两个四边形的公共边都互相平行’这一条件可不可以去掉？”，“通过棱柱的概念我们得知，棱柱的侧面都是平行四边形，那么，可不可以改为‘有两个面互相平行，其余各面都是平行四边形的多面体叫做棱柱’？”立体几何部分非常考察学生的直观想象能力，而立体感和直观想象能力是要通过日常训练来培养的.因此，问题抛出后，切记不要迅速给出答案，要学会等待，给学生留足思考时间，使其经历充分的思考和想象，先与自己对话；然后安排小组讨论，进行生生对话，思维角度的不同使学生产生自主交流的欲望，小组讨论的过程便是学生互相之间思想交流和碰撞的过程，最后是师生间的对话，请学生阐述问题探究中的困惑与收获，总结问题解决的方法，体会数学概念的严密，培养细致的习惯.

课堂对话是另一种形式上的“慢”教学，它使学生在相互交流的过程中，感悟不同的思考方式、思考方法，完善自己的认知，借鉴同伴的优点，丰富学习体验与学习感悟.“慢交流”使学生学得细致，学得深入，学得透彻，提高学生多角度分析问题的能力及团结协作能力.

“教育是慢的艺术”，唯有自由之时间，才能有自由之思想；数学有思考，才能灵动[3].在快速行进的课堂中，学生是被“拽”着往前走的，是被动的；所以“慢”教育理念给教育提供了新的视角.“慢”教育的目的是在“慢”中给学生足够的空间，使他们勇于思考；在交流碰撞中学会思考，在收获的喜悦中乐于思考.教师应该积极探索如何在实际教学中把握好“慢”，何时“慢”，何处“慢”？要在“慢”中寻高效，向“慢”要能力提升，唯有如此，才能让学生深刻理解数学的本质，真正会用数学的方法去思考问题、解决问题，从而提升自身学科素养.