基于VMD-Teager的非平稳振动时频特性研究

2021-02-22李占龙刘林霞曹俊琴

兵器装备工程学报 2021年1期

李占龙,刘林霞,李虹,孙宝,曹俊琴

(1.太原科技大学机械工程学院，太原 030024； 2.太原科技大学电子信息工程学院，太原 030024；3.太原科技大学应用科学学院，太原 030024)

大型特种车辆因工况复杂、工作环境多变等因素，在行驶过程中必然引起强烈的振动，不仅会对车辆的关键部件造成损伤，更会直接影响驾驶人员的舒适性。因此，对车辆振动特性的研究是十分有必要的。在振动信号采集过程中常受其他信号的干扰，最终采集的信号多为复杂非平稳振动信号，给信号处理及振动特性分析增加了难度。因此，如何对非平稳振动信号有效分解并提取其有用成分，是亟待深入研究的问题。

针对此类机械设备中的非平稳振动信号，许多学者做了大量研究。张俊红等[1]采用经验模态分解(Empircical Mode Decomposition，EMD)对柴油机机体振动信号进行分解，并以分解后分量经小波时频变换得到的时频分析结果为依据对柴油机结构进行优化，最终整机振动强度明显降低。李小珍等[2]利用传统小波变换研究高速铁路轨道、桥梁等位置的振动传递特性，得出了不同位置振动响应与车速间的关系。贾继德等[3]将同步压缩小波变换(SWT)与短时傅里叶变换(STFT)、连续小波变换(CWT)等方法作比较，结果表明，SWT对信号的重构效果均优于其他方法，最后将其应用到发动机振动信号分析中，有效揭示了发动机磨损信号的变化规律。

2014年，国外学者K.Dragomiretskiy等[4]提出了一种新的自适应非平稳信号处理方法—变分模态分解(Variational mode decomposition,VMD)，VMD克服了EMD分解存在的模态混叠等问题，且不涉及类似小波变换中小波基函数的选择问题。近年来越来越多的学者将其应用于众多领域的信号分析中[5-8]。文献[9-10]将VMD分别应用于铣削加工颤振检测和滚动轴承振动状态监测中，成功实现了颤振检测提取和轴承运行状态的特征提取。由于在求解信号的瞬时频率时，Teager能量算子不需做复数计算，响应快，可快速跟踪瞬时变化信号的频率和幅值，与Hilbert变换相比，对揭示瞬时频率的突变情况有很好的效果，且Teager能量算子解调比Hilbert解调能力强[11]，许多学者选择Teager能量算子对分解后分量进行解调。马增强、徐波等人将变分模态分解和Teager能量算子结合成功应用到滚动轴承和重型机械设备的故障特征提取中[12-13]。

本研究采用VMD与Teager能量算子解调结合对3种典型非平稳振动信号进行分析，通过VMD对非平稳振动信号进行分解，并利用Teager能量算子解调作时频分析，以研究该类信号的时频特性。

1 理论方法

1.1 变分模态分解

VMD算法实质是基于经典维纳滤波、希尔伯特变换和混频理论，在变分框架中解决复杂信号分解的变分问题求解过程。通过搜寻约束变分模型最优解来实现信号自适应分解，将一个实信号f分解为K个带宽有限的模态，并得到每个模态的带宽和对应的中心频率。

VMD将分解得到的每个模态(即本征模态函数IMF)重新定义为一个调幅调频信号，表达式如下：

uk(t)=Ak(t)cos[φk(t)]

(1)

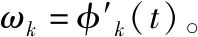
为确定每个模态的带宽，需构造变分模型，步骤如下：

1) 对每个模态uk(t)进行希尔伯特(Hilbert)变换，得到模态函数的解析信号：

(2)

2) 对得到的解析信号乘以指数项e-jωkt，可调整估计的中心频率，将对应的频谱调制到相应的基频带：

(3)

3) 对式(2)中的解调信号先进行H1高斯平滑估计，通过计算其梯度的平方L2范数，最终得到估计的各模态分量带宽。约束变分模型表达式如下：

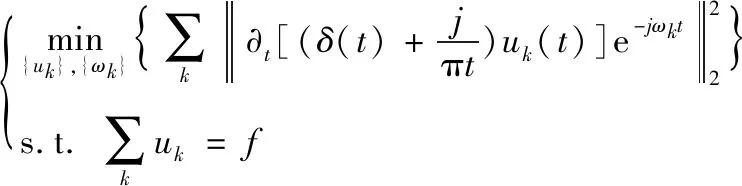
(4)

式(4)中，{uk}={u1,…,uk}为分解得到的k个IMF分量；{ωk}={ω1,…,ωk}代表各IMF分量对应的中心频率；f为原始信号。

为求取上述约束变分模型的最优解，即各个模态函数，引入二次惩罚因子α和拉格朗日乘法算子λ(t)，构造如下形式的Lagrange表达式：

(5)

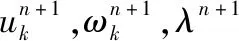
(6)

利用在L2范数下的Parseval/Plancherel傅里叶等距变换法,将式(6)变换到频域中，其表达式为

(7)

(8)

(9)

(10)

(11)

迭代停止条件为

(12)

其中，判定精度ε>0。

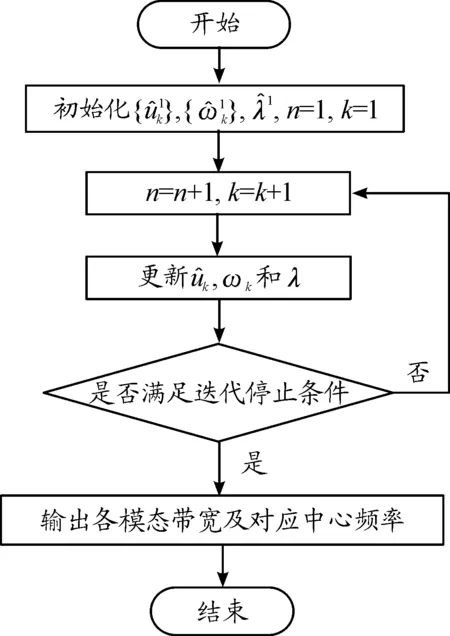
图1 VMD算法流程框图

1.2 基于互信息准则的VMD分解个数的确定

利用VMD算法对信号作分解时，需提前设定惩罚因子α和模态分解个数K的值。本文中惩罚因子α根据参考文献[11]取2 000，分解个数K根据互信息准则来确定。

互信息(mutual information)可表示两随机变量信息熵的差值，即两随机变量间的相关程度，其定义如下：

I(M|N)=H(M)-H(M|N)

(13)

式中,M、N为两个不同的随机变量；H(M)为M的信息熵；H(M|N) 为N对应M的条件信息熵。对上述互信息作归一化处理Ii/max(Ii)，通过比较归一化后的互信息值与阈值0.02[14]的大小，以确定VMD算法分解个数K。

1.3 Teager能量算子解调

Teager能量算子是一种非线性差分算子，时间分辨率高，计算过程简单快速，可及时跟踪信号的波形变化，经常用于信号解调分析中[15]。对实信号经VMD得到的各IMF分量作Teager能量算子解调，计算各分量的瞬时频率和瞬时幅值，通过得到的实信号时频分布信息绘制二维时频图来作时频分析。

对于连续时间信号和离散信号，Teager能量算子的定义分别如下：

(14)

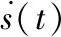
ψ[s(n)]=s2(n)-s(n+1)s(n-1)

(15)

式中，s(n)为原始离散时间信号。

由式(15)可知，离散时间信号每一时刻算子的计算量小，只需3个样本数据即可。通过式(16)可求出单分量调幅调频信号的瞬时频率和瞬时幅值[11]：

(16)

1.4 VMD-Teager时频分析法

文中采用的VMD-Teager方法流程图如图2所示。首先利用VMD方法对原始非平稳振动信号进行分解，再将分解得到的各IMF分量作Teager能量算子解调，得到各分量的瞬时频率和瞬时幅值，进而作时频分析。

2 算例分析

现场采集的机械设备振动信号普遍存在强脉冲干扰和背景噪声，某些旋转机械结构和往复做功机械结构均存在间断性信号。为研究VMD-Teager方法对典型非平稳振动信号的有效性，构造了分别含噪声、间断和脉冲干扰信号的3组典型非平稳振动信号，对比研究了VMD和EMD方法的分解能力，并对各分量作Teager能量算子解调，对其时频分析以进一步评价VMD-Teager方法的有效性。

图2 VMD-Teager时频分析法流程框图

2.1 含噪声非平稳振动信号分析

振动信号f1(t)(含噪声)由调幅信号f11(t)、调幅调频信号f12(t)和随机噪声f13(t)组成，图3为f1(t)时域图。图4为f1(t)分别经EMD和VMD方法分解得到的图形。

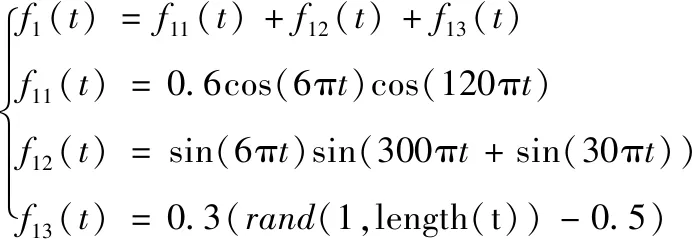
(17)

由图4(a)可知：EMD将信号分解为8个分量，IMF1的幅值和周期分别约为0.9和0.2 s，与f12(t)对应，IMF2在0.4～0.75 s特征与f11(t)相符，但其他时间段波形出现缺失，IMF3～IMF5包含正弦信号，但未明显观察出其与f1(t)各组分特征相似，对比图3原始信号失真严重；由图4(b)可知VMD分解得到3个分量，IMF1的幅值和周期分别约为0.6和0.2 s，与f11(t)的特征相符，IMF2的幅值和周期分别约为0.9和0.2 s，与f12(t)对应，IMF3波形无明显规律，与随机噪声信号f13(t)对应，可将原始信号f1(t)有效准确分解。

综上可知：EMD得到的分量个数较多且存在虚假分量，而VMD可将含噪声非平稳振动信号准确分解，因此，VMD对含噪声非平稳振动信号的分解效果优于EMD。下文通过比较VMD与f1(t)的频谱图以进一步验证VMD的有效性。

表1为信号f1(t)经VMD方法分解前后频率和幅值的对比。由表1可知，信号f1(t)经VMD方法分解后频率成分未发生变化，各频率成分幅值变化范围为0.2%～1.6%，进一步说明VMD对含噪声非平稳振动信号具有良好的分解效果。

图3 非平稳振动信号f1(t)及其分量的时域图

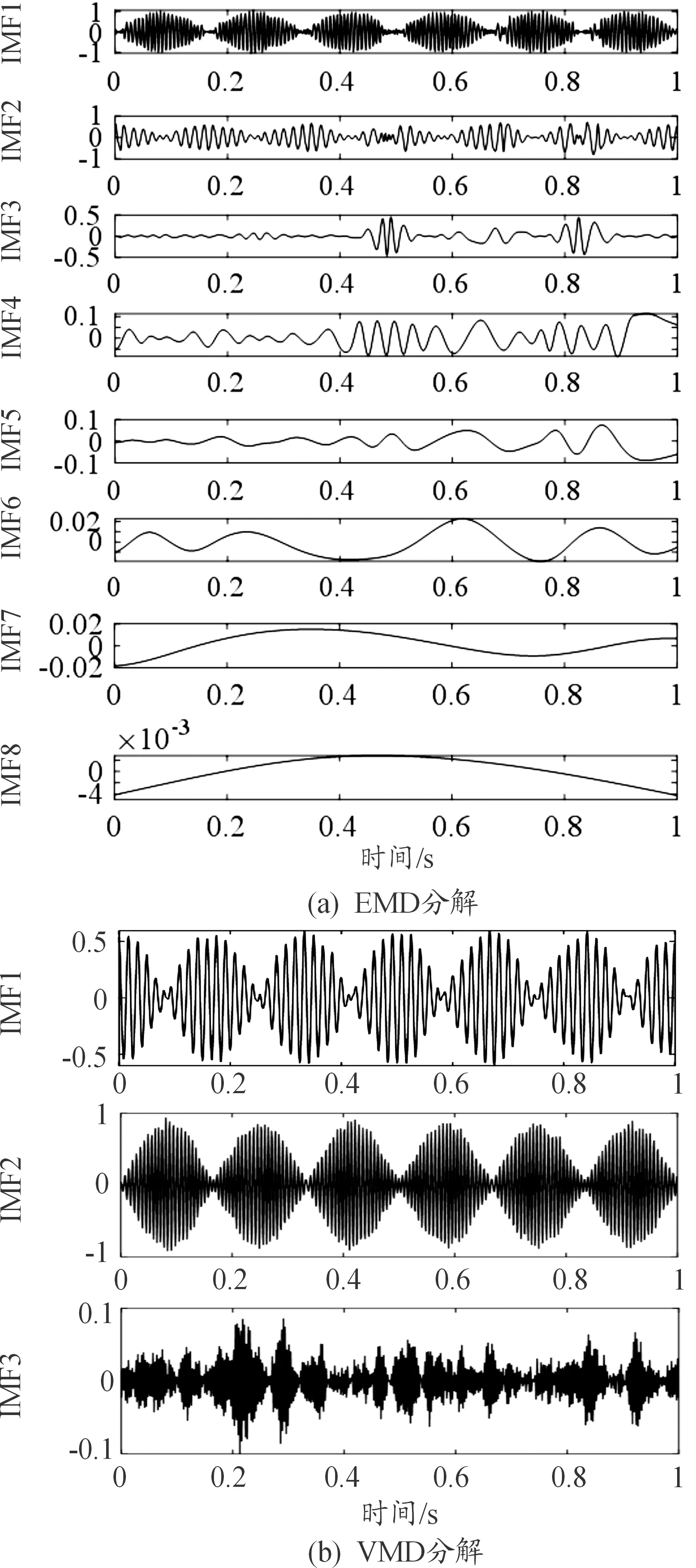
图4 信号f1(t)的两种分解图

表1 信号f1(t)分解前后频率幅值对比

2.2 含间断信号非平稳振动信号分析

非平稳振动信号f2(t)(含间断信号)由正弦信号f21(t)、线性调频信号f22(t)和间断信号f23(t)组成，图5为f2(t)的时域图，图6为f2(t)经EMD和VMD方法分解得到的图形。

(18)

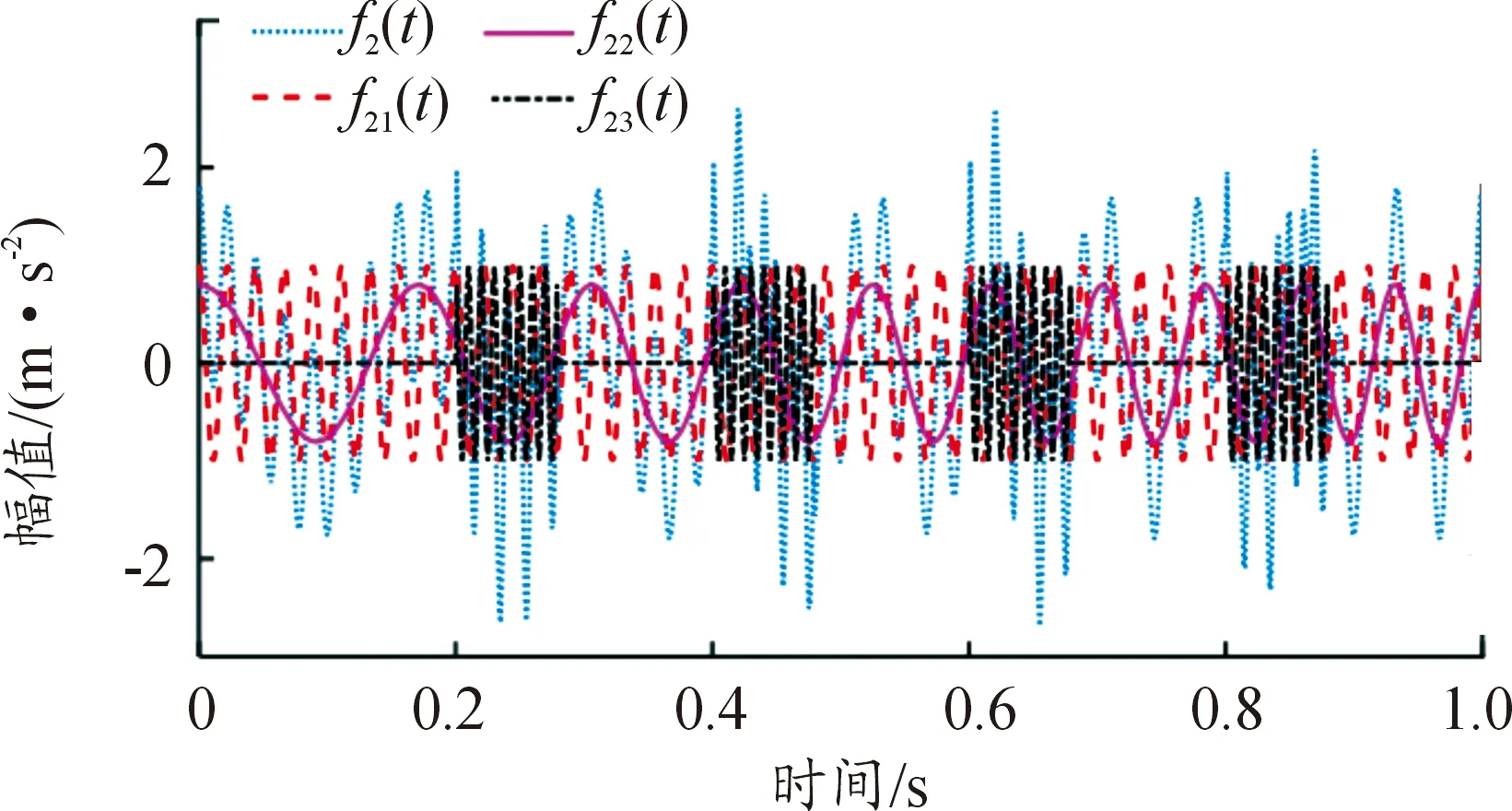
图5 非平稳振动信号f2(t)及其分量的时域图

由图6(a)可知：EMD将信号分解为6个分量，IMF1幅值与f21(t)相符，但在间断信号f23(t)存在的时候出现了信号失真，IMF2、IMF3的特征对应间断信号f23(t)，其余分量特征与f2(t)中各信号不符，为虚假分量，对比图5原信号失真严重；由图6(b)可知VMD分解得到3个分量，其中IMF1与线性调频信号f22(t)对应，幅值约为0.8，IMF2、IMF3分别对应正弦信号f21(t)和间断信号f23(t)，可将原始信号有效准确分解。表2为信号f2(t)经VMD方法分解前后频率和幅值的对比。由表2可知，信号f2(t)经VMD方法分解前后频率成分未变，幅值发生0.2%～1.2%的变化。综上，VMD方法不受间断信号的干扰，可将含间断信号的非平稳振动信号f2(t)有效分解。

图6 信号f2(t)的两种分解图

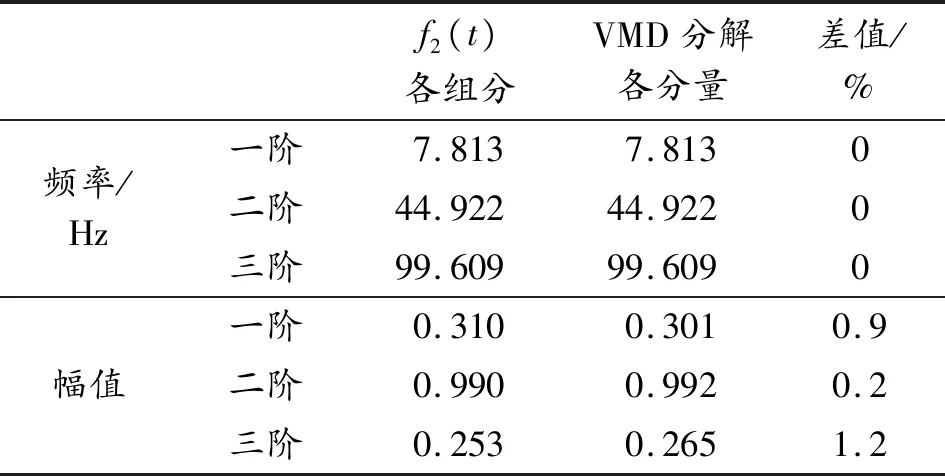
表2 信号f2(t)分解前后频率幅值对比

2.3 含脉冲信号非平稳振动信号分析

振动信号f3(t)(含脉冲干扰信号)由两个正弦信号f31(t)、f32(t)和脉冲干扰信号f33(t)组成，其时域图如图7所示。图8为f3(t)EMD和VMD得到的。

(19)

图7 非平稳振动信号f3(t)及其分量的时域波形

图8 信号f3(t)的两种分解结果

由图8(a)可知：EMD将信号分解为6个分量，IMF1与正弦信号f32(t)特征相符，但IMF1受脉冲信号影响较大，导致其波形失真，EMD的其余分量部分特征与f3(t)中各组分特征相符，但各分量间模态混叠现象严重，对比图7原始信号失真严重；由图8(b)可知：VMD分解得到3个分量，IMF1与f31(t)特征相符，IMF3与脉冲信号f33(t)对应，幅值出现了一定程度的失真。表3为信号f3(t)经VMD方法分解前后频率和幅值的对比。由表3知，f3(t)经VMD方法分解前后频率成分未发生变化，幅值变化范围为0～1%，基本可忽略。综上，VMD方法对含脉冲非平稳振动信号的分解效果比EMD方法好，可将此类非平稳振动信号中各组分有效分解。

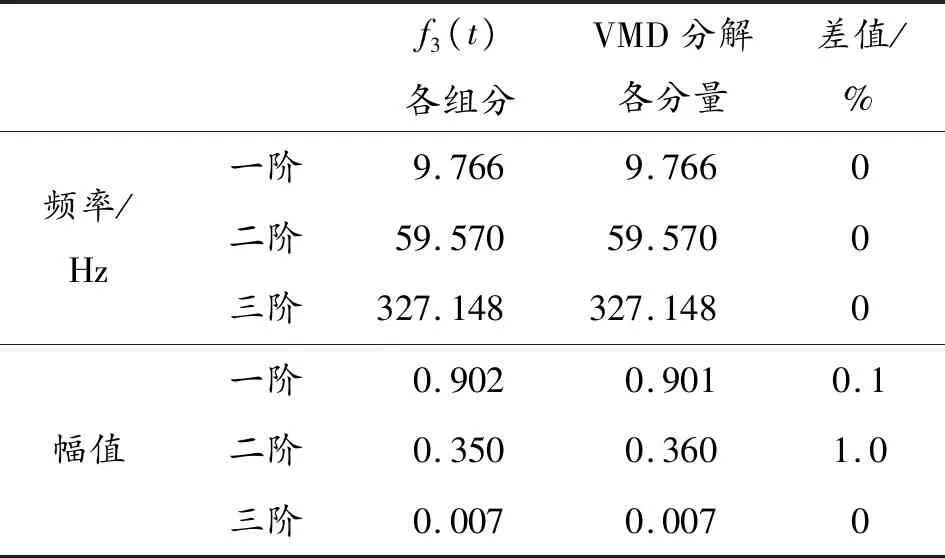
表3 信号f3(t)分解前后频率幅值对比

同时，利用EEMD对上述三类信号进行了分解，对比结果显示，EEMD可抑制EMD的模态混叠，但依然存在算法效率低、分解个数过多和精度不足的弊端，限于篇幅，本文不做赘述。综上，VMD分解个数可进行优化，对3种典型非平稳振动信号的分解效果均较理想，后文将对VMD的分量作Teager能量算子解调以进行时频分析。

3 时频域分析

对上述3组典型非平稳振动信号经VMD得到的IMF分量作Teager能量解调，通过计算所得的瞬时频率和瞬时幅值绘制二维时频图，最后分析频率随时间变化的规律以验证VMD-Teager方法的有效性。三组典型非平稳振动信号的二维时频图如图9所示。

从图9(a)可以看出：f1(t)的3个分信号的中心频率56、153、362 Hz被清晰的刻画出来，其中随机噪声f13(t)对应的362 Hz频率随时间变化无明显规律，与噪声信号的特征相符；图9(b)中100 Hz的间断信号f23(t)在0.2～0.28 s、0.4～0.48 s、0.6～0.68 s和0.8～0.88 s出现，45 Hz的频率对应正弦信号f21(t)，线性调频信号f22(t)也清晰可见；图9(c)中正弦信号f31(t)、f32(t)分别对应的中心频率10 Hz、60 Hz 及其边频带清晰可辨，同时在0.25 s、0.45 s、0.65 s、0.85 s处脉冲信号f33(t)也对应出现。综上可知，VMD方法对3种典型非平稳振动信号的分解效果显著，经Teager能量算子解调作时频分析可清晰揭示信号的瞬时频率和幅值随时间变化的规律。因此，采用VMD-Teager方法对非平稳振动信号作时频分析效果良好。