粒子群算法的负载敏感阀节流槽结构的优化
2021-02-22吴卫东蔡树文周兴平
吴卫东,丁 一,蔡树文,徐 威,周兴平
(黑龙江科技大学 机械工程学院, 哈尔滨 150022)
0 引 言
随着我国现代化矿井的快速发展,矿山生产对掘进机、液压凿装机、液压支架等开采设备的先进性有了更高的要求[1-2],尤其对开采设备液压系统的性能提出了更高的要求。负载敏感阀作为液压传动系统的重要部件,控制着多个执行机构的协同动作,因此,液压阀工作性能的提高可以促进液压系统整体工作性能的提升[3-4]。
为了提高液压系统适用范围和实用性,一般情况下,负载敏感阀节流槽可以满足不同工况的流量要求,也可以减小液压系统的波动[5],但是当系统要求可靠性比较高、动态特性比较大时,常规的节流槽结构并不能完全满足现有的要求。因此,学者们对节流槽的研究取得了丰硕的研究成果[6-8]。冀宏等[9-10]通过对典型节流槽阀口过流面积的研究,得出了两种节流槽数学模型并解释了气穴及液压噪声的形成机理。王东升等[11]采用过流面积与阀口流量系数相结合的方法,研究了节流槽阀口的稳态液动力和流量特性,分析了U+V型等组合式对节流槽流量特性的影响。Borghi等[12]得到了典型节流槽与组合型节流槽在不同阀口开度下流量、压力损失和液动力等相关数据。
现代优化设计方法中粒子群算法适用于全局搜索、非线性优化,李维嘉等[13]研究了基于粒子群算法的滑阀节流槽的优化设计,其研究成果对利用粒子群算法进行具体对象的优化具有一定的指导意义。姜涛等[14]采用粒子群算法对多路换向阀换向耦合节流结构拓扑进行了研究。上述研究工作都为节流阀的设计与优化奠定了一定的基础笔者在U型节流槽的研究基础上,提出一种Ω型结构节流槽,建立阀口过流面积数学模型,利用粒子群算法对其结构参数进行寻优,运用FLUENT仿真软件对其性能进行检测并验证仿真结果。
1 阀芯节流槽过流面积
节流槽阀口面积的合理分配不仅能够缓冲工作产生的冲击震荡,还能有效提高机构换向操作的舒适度。因此,深入研究阀口形式的多样性,对获取阀口过流面积与阀口开度之间的关系式至关重要。节流槽阀口主要分为全周开口和非全周开口两种形式,不同形式的阀口主要影响阀内油液的流动特性。
1.1 U型节流槽
U型节流槽结构如图1所示。U型节流槽分为两部分:一部分为半圆形结构;另一部分为矩形结构。当阀内油液流经U型节流槽时油液先经过上表面A1流入,在经过纵截面A2流出。

图1 U型节流槽结构Fig. 1 Structure of flow area of U-type
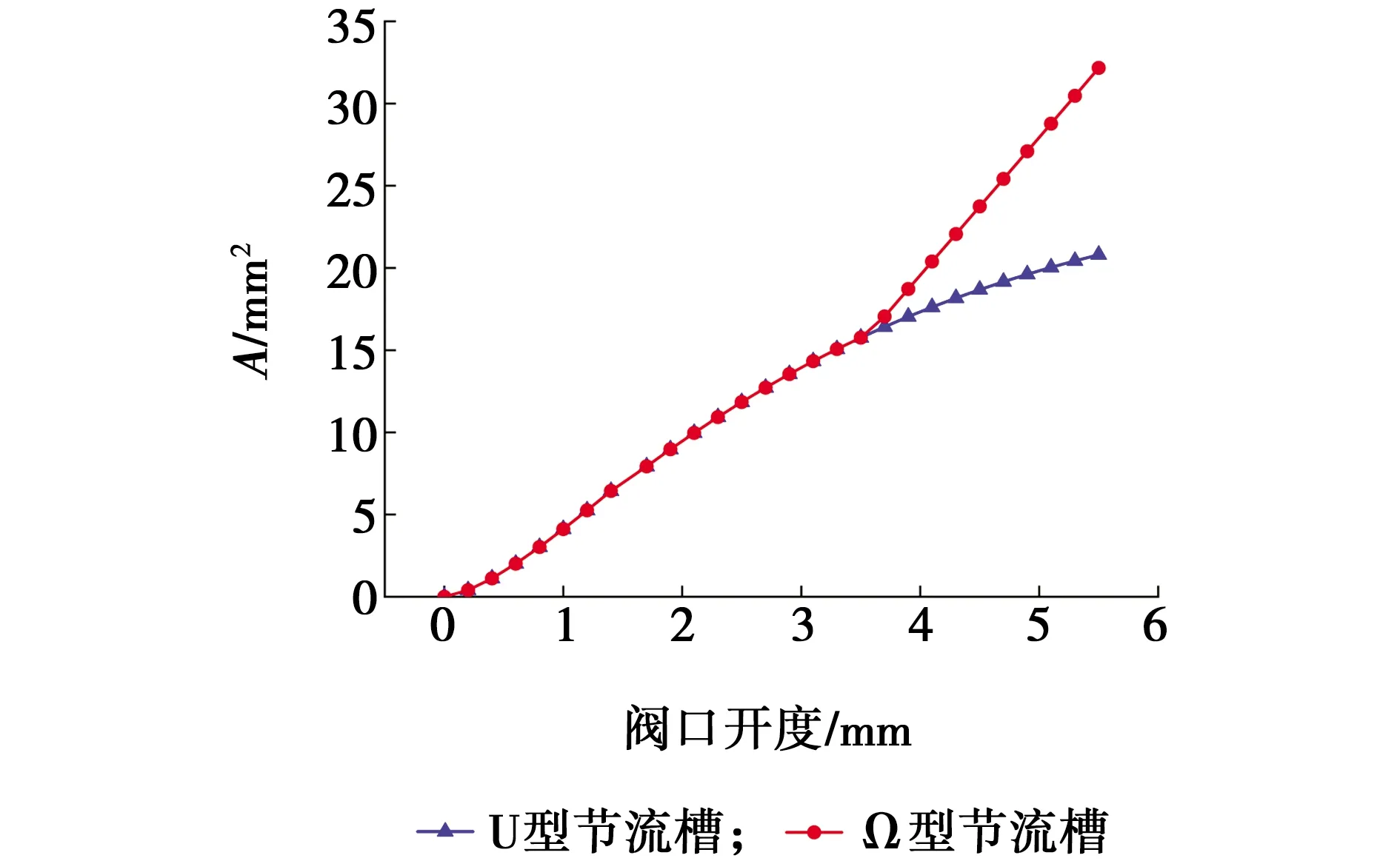
(1)阀口开度0 α=2arccos ((r-x)/r), β=2arcsinL/R, 式中:L——阀口开度x时节流槽宽度的1/2,mm; r——Ω节流槽的半径,mm; x——阀口开度,mm; α——阀口开度与中线夹角; A1——横向表面积,mm2; At——横向总表面积,mm2; D——节流槽圆弧纵向投影深度,mm; R——阀芯半径,mm; β——节流槽与中心的夹角 A2——纵向截面积,mm2; h——节流槽深度,mm; A——节流槽过流面积,mm2; n——节流槽的个数 (2)当阀口开度r L=r, β=2arcsinr/R, 式中:L1——节流槽总长度,mm。 Ω型节流槽结构如图2所示。当阀内油液流经Ω型节流槽时油液先经过上表面A1流入,在经过纵截面A2流出。随着阀口开度的增大,Ω型节流槽过流面积分为三部分,第一部分为半圆形结构,第二部分为矩形结构,此时Ω型与U型过流面积相同。阀口开度继续增大,进入渐开型结构,推导公式如下。 当阀口开度c β=2arcsinL/R, At=AU1+AΩ1, 式中:c——U型节流槽边长,mm; l——Ω节流槽的底边长度,mm; AU1——横向U型表面积,mm2; AΩ1——横向Ω型表面,mm2; At——横向总表面积,mm2; AΩ2——纵向截面积,mm2。 图2 Ω型节流槽结构Fig. 2 Structure of flow area of Ω-type 粒子群中的每一个粒子都代表一个问题的可能解,通过粒子个体的简单行为,群体内的信息交互实现问题求解的智能性[16]。算法流程如下: (1)初始化粒子群,随机性的速度和位置。假设所求解问题的自变量有n1维,种群大小为N,初始化粒子群的位置信息表示为 式中,xji(0)——第0代粒子群中第i个粒子的第j个分量的位置。 同理,初始化粒子的速度信息可以表示为 vji——第0代粒子群中的第i个粒子的第j个分量的速度。 (2)根据适应度函数计算粒子适应度值。将每个粒子当前的适应度函数值与其最佳个体历史位置对应适应值做比较,如果当前的适应度值高,则将当前位置更新为历史最佳位置。将每个粒子当前的适应度函数值与其最佳全局历史位置对应适应值做比较,如果当前的适应度值高,则将当前位置更新为全局历史最佳位置[17]。 (3)粒子速度更新公式和位置信息更新公式。在每次迭代过程中,粒子通过个体极值和全局极值来更新自己的速度信息和位置信息,即: 式中:ω——惯性权重,是保持原来速度的系数; c1、c2——学习因子; k——当前迭代次数; ξ、η——均匀分布于[0,1]区间内的随机数。 如果未满足结束条件,反复执行,直到达到最大进化代数,或达到所要求的收敛精度。 基于流体仿真所得的阀口流量,形成粒子寻最优解的判断标准,以Ω节流槽的结构尺寸参数为设计变量,建立优化模型,完成对负载敏感阀节流槽结构的优化设计。根据负载敏感阀调节方向时耦合阀口开度-过流面积的线性关系,可以得出阀口的开度和流量同样呈线性变化,且阀口流量呈连续变化。因此,在对满足负载敏感阀工作时阀口流量变化需求的节流槽进行优化设计时,将不同阀口开度下理论计算流量与流体仿真所得阀口流量的方差和设置为优化模型的目标函数为 式中:m——不同阀口开度下个数; qj——阀口开度第j个对应流量,文中取值见表1; fj(x)——阀口开度下第j个理论计算值; s——方差。 表1 定压差阀口开度流量 采用粒子群优化算法对节流槽结构参数进行优化设计时,在优化过程中变量维数n1=3,种群的粒子总数N=40,c1、c2为自我学习因子以及群体学习因子,控制粒子向个体和全局最优位置移动的最大步长,通常取2;惯性权重w,描述上一代速度对目前速度的影响值,可以调节粒子的移动速度,w较大时全局寻优能力强,个体寻优能力弱,反之个体寻优能力强,群体寻优能力弱,通常使算法在个体与全局寻优得到平衡,前期有较高的全局搜索能力,后期有较高的个体搜索能力以提高收敛精度,w选取0.7能有较高的稳定性[18-19]。优化算法流程如图3所示。 为了满足定压差条件下节流槽阀口开度-流量特性的要求,选用粒子群算法完成对流体仿真实验样本的优化设计,选取不同的阀口开度以及相应的流量带入到优化算法中,以设定的负载敏感阀流体仿真所得的工作口流量为评价目标,得到目标函数值的最小值为0.013。通过寻优设计、理论计算,得出样本对应的设计值r=1.545 mm、L1=4.792 mm、h=4.700 mm。根据实际加工,最终选择节流槽的最优结构尺寸参数r=1.500 mm,L1=4.800 mm,h=4.700 mm,在Matlab软件中运行阀口过流面积公式,代入上述最优解,得出两种不同形状的节流槽阀口开度阀口-过流面积曲线如图4所示。 图3 优化算法流程Fig. 3 Optimization algorithm flow 图4 两种节流槽的过流面积Fig. 4 Flow area of two kinds of throttle grooves 由图4可知,U型与Ω型节流槽阀口过流面积均呈现分段增大的趋势。曲线具有两个明显拐点,第一个拐点为阀口开度为1.5 mm,第二个拐点为阀口开度为3.0 mm。在第一个拐点前后,平均面积梯度由4.56 mm2/mm增大至4.92 mm2/mm。在第二个拐点之前,U型与Ω型过流面积梯度一致,在第二个拐点之后,U型节流槽过流面积梯度逐渐减小,Ω型节流槽过流面积梯度增大,相比较平均增大32.66%,具有较高的流量增益。 采用FLUENT仿真软件,当入口压力4.9 MPa、出口压力3.0 MPa时,U型节流槽以及Ω型节流槽速度如图5和6所示。将流体进行可视化分析,化分为B1、B2、B3、B4四个区域,当流体从过流面A1经过时,由于过流面积减小,B1区域的流体速度有所提高;当流体从过流面A2经过时过流面积突然收缩,B2区域速度达到最大值;经过A3过流面时,B3区域过流面积增大,速度相应有所下降,同时流体冲击到阀芯壁面降速,最后流经A4后,过流面积再次增大,B4区域流速下降。不同阀口开度下两种节流槽速度峰值对比见表2。 图5 不同形式节流槽速度云图 Fig. 5 Speed cloud diagram of different forms of throttle groove 图6 不同形式节流槽速度矢量Fig. 6 Different forms of throttle speed vector 表2 定压差两种节流槽速度峰值 由图5、6可知,随着阀口开度的增大,高流速区域面积也逐渐增大,B3区域产生速度峰值,Ω型节流槽速度梯度明显小于U型节流槽,旋涡减小。由表2可知,Ω型节流槽速度峰值比U型节流槽平均减小4%,缓解了对节流槽的冲击,稳定性相对提高。 (1)建立了Ω型节流槽的过流面积数学模型,得出等效过流面积,采用粒子群优化算法对节流槽结构进行寻优,得到满足流量增益的设计参数的最优值为r为1.5 mm、L1为5.6 mm、h为4.7 mm。 (2)对比Ω型节流槽以及U型节流槽的过流面积,当阀口开度小于3.0 mm时,二者过流面积梯度一致;阀口开度大于3.0 mm时,Ω型节流槽过流面积梯度增大,U型节流槽过流面积梯度逐渐减小,Ω型比U型平均增大32.66%,增大了流量调节范围,适应于机构的快速要求。 (3)在定压差条件下,对比分析了六组不同阀口开度下Ω型与U型节流槽速度梯度的仿真结果,Ω型节流槽速度梯度明显小于U型节流槽,速度峰值平均减小4%,对节流槽冲击减小,稳定性相对提高。1.2 Ω型节流槽

2 Ω型节流槽结构优化
2.1 节流槽的优化原理



2.2 节流槽优化模型的建立


3 FLUENT仿真验证



4 结 论
