《立体几何》专题训练

王慕晓

一、选择题

1.魏晋时期数学家刘徽在他的著作《九章算术注》中，称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”，刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比应为π：4.若正方体的棱长为2，则“牟合方盖”的体积为（） .

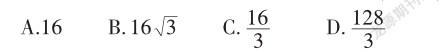
2.关于三个不同平面α，β，γ与直线l，下列命题中的假命题是（）.

A.若α⊥β，则α内一定存在直线平行于β

B.若α与β不垂直，则α内一定不存在直线垂直于β

C.若α⊥γ，β⊥γ，α？β=l，则l⊥γ

D.若α⊥β，则α内所有直线垂直于β

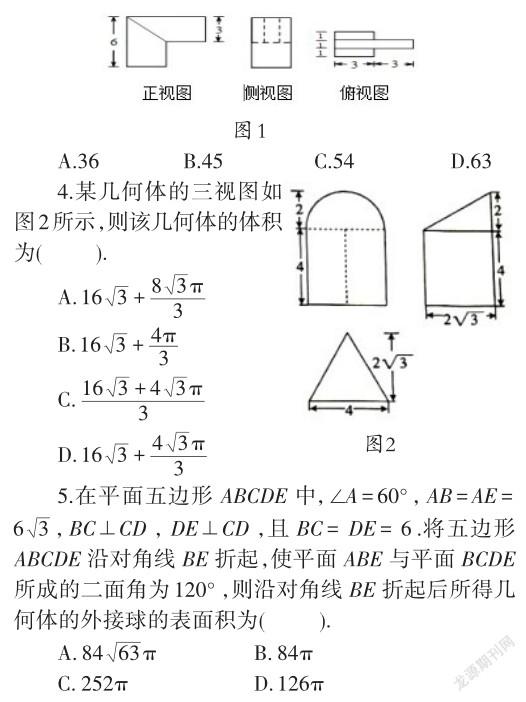
3.榫卯是我国古代工匠极为精巧的发明，它是在两个构件上采用凹凸部位相结合的一种连接方式.广泛用于建筑，同时也广泛用于家具.我国的北京紫禁城，山西悬空寺，福建宁德的廊桥等建筑都用到了榫卯结构，榫卯结构中凸出部分叫榫（或叫榫头），已知某“榫头”的三视图如图1所示，则该“榫头”的体积是（）.

13.已知直線m与球O有且只有一个公共点，从直线m出发的两个半平面α、β截球O所得两个截面圆的半径分别为1和2，二面角α-m-β的平面角为120°，则球O的表面积等于______.

三、解答题

14.如图5，在三棱柱ADF-BCE中，平面ABCD⊥平面ABEF，侧面ABCD为平行四边形，侧面ABEF为正方形，AC⊥AB，AC=2AB=4，M为FD的中点.

（1）求证：FB//平面ACM；