求空间角的三种思路

陈玲

立体几何中的空间角问题在高考数学试题中扮演着“常客”的角色，主要考查立体几何中异面直线之间所成角、直线与平面所成的角、二面角的定义以及求法.下面.笔者重点介绍三种求空间角的思路，以帮助同学们提升解题的效率.

一、采用平移法求空间角

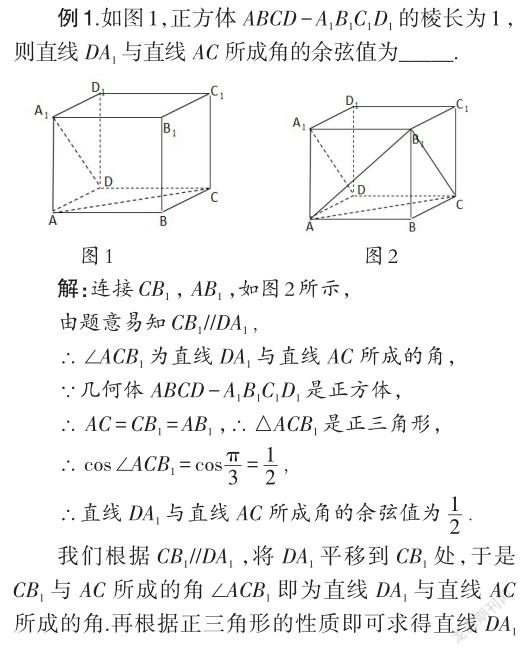
平移法是指将某个图形沿着一定的方向移动一定的距离，利用平移变换及其性质解题.值得注意的是，平移前后图形的大小、形状不改变，对应点之间的距离都相等，且都等于平移的距离.运用平移法求解立体几何中的空间角问题，一般需将所求的直线或者平面平移到与另一条直线或者平面相交的位置，而所得的夹角与所求的空间角的大小相等.再根据勾股定理、点到直线的距离公式、三角形的性质、正余弦定理、三角函数的定义便可求得夹角的大小.

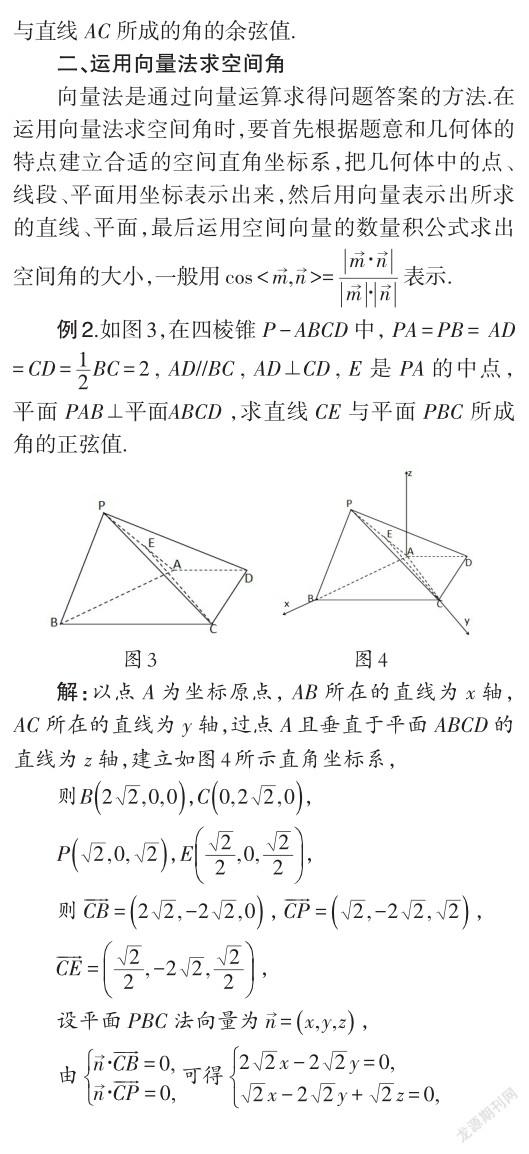
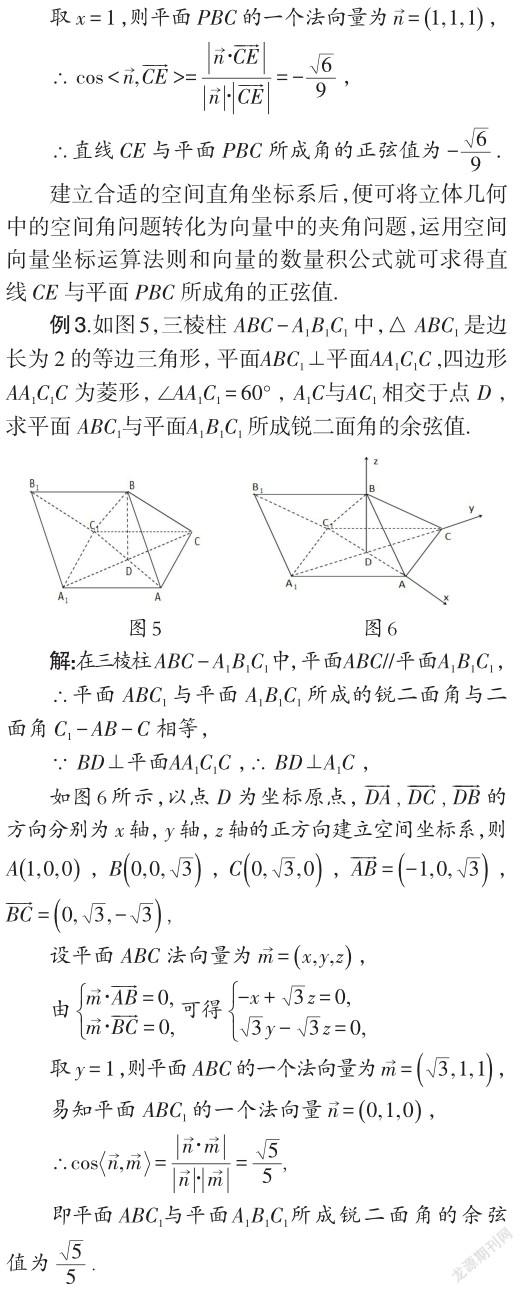
在运用向量法求立体几何的空间角时，还应结合图形对空间角的大小作出大致的判断，以便确定所求向量之间的夹角等于空间角的平面角还是其补角，进而得到正确的结果.

三、借助垂面法求空间角

垂面法是借助垂面与平面之间的垂直关系来解题的方法.我们知道，以二面角的公共直线上的任意一点为端点，在两个面内分别作垂直于公共直线的两条射线，这两条射线所成的角叫做二面角的平面角.运用垂面法求解空间角问题，需根据几何体的结构特征找到或作出与两平面之间的交线的垂面，便可根据二面角的平面角的定义确定所求二面角的平面角，再在垂面中借助平面几何知识，如正余弦定理、勾股定理、三角形的性质等求出二面角的平面角的大小.

例4.如图7，四棱锥P-ABCD中，PA⊥平面ABCD ，四边形ABCD为菱形，∠ADC=60°，PA= AD= 2 ， E是AD的中点，求二面角A-PD-C的正弦值.

我们根据题意和图形可发现，AD为平面APD与平面PDC的交线，于是过点E作EM⊥PD于M，连接CM，便作出平面APD與平面PDC的垂面EMC，得出二面角A-PD-C的平面角为∠EMC，再在垂面EMC上根据勾股定理求得二面角的平面角.

相比较而言，第一种思路较为简单、直接，应用较多；第二种思路只适用于求解方便建立空间直角坐标系的问题；第三种思路仅适用于求解二面角的两个半平面相交的二面角问题.

（作者单位：甘肃省敦煌中学）