基于ANSYS的叶蜡石高温高压腔体温度场模拟分析

邓福铭，宋美娇，陈为芳

（中国矿业大学（北京）超硬刀具材料研究所，北京 100083）

0 引言

随着近年来对人造金刚石需求量的逐渐增加，在人造金刚石合成过程中，叶蜡石由于其良好的传压性、密封性、耐热保温性、绝缘性及机械加工性，在人造金刚石、立方氮化硼等超硬材料高压合成行业中常常作为密封传压介质原料而得到广泛的应用[1-3]。

叶蜡石的隔热保温性可直接通过其热导率反映出来，温度和压力的作用对其导热性有很大的影响，研究叶蜡石高温高压下导热特性对于准确了解高压合成过程中的温度变化有重要意义，D.L.Decker等[4]研究发现室温下在平行于（001）晶面方向上随着压力的增加，叶蜡石热导率在13～15 mcal/（cm·s·K）范围内增加，但经过850 ℃烘烤后热导率显著降低，同时随压力增加而减小。J.H.Ter Heege等[5]对叶蜡石热导率在2.5 GPa、400～1000 ℃范围内测试分析认为，随着温度的增加叶蜡石的导电率在（7.2～8.3）×10-7Ω·m范围内也相应增加。与计算机相结合的模拟分析技术是当今社会生产行业发展的一种趋势，在金刚石高温高压合成工程中，实际高压腔体内的温度、压力直接测量是非常困难的。孟令启等[6]曾运用有限元软件ANSYS对金刚石压机机架进行过有限元分析。李瑞、马红安等[7-10]采用有限元软件ANSYS/LS-DYNA对六面顶加压方式下叶蜡石的流变行为进行了模拟仿真，给出了叶蜡石内压力分布的数值分析结果，同时研究了焙烧温度对叶蜡石块传压性能的影响。利用计算机模拟仿真可以直观了解内部温度压力情况，但迄今利用有限元分析软件对六面顶压机高温高压腔体内温度场、压力场进行系统定量的数值模拟分析，国内外对于此方面的研究及文献报道并不多。

本文采用综合物性测量系统PPMS和LFA427激光热导仪测试了高压高温作用前后叶蜡石腔体不同区域的热导率，并利用有限元分析软件ANSYS，采用3组不同的叶蜡石热导率数据分别对叶蜡石块的3种不同组装方式合成腔体温度场进行了计算机模拟分析。确定了更准确的叶蜡石导热物性参数，为金刚石合成腔体温度场可视化提供了理论数据支持。

1 实验方法

叶蜡石的热导率可直接反映其隔热保温性的优异，本文选取北京门头沟叶蜡石，经过除杂、破碎、混料、成型、焙烧等一系列工序得到叶蜡石块，将焙烧后的叶蜡石块与白云石、导电堵头等进行组装，采用六面顶压机进行合成实验，对反应后叶蜡石取样、分区、打磨，分别制取尺寸为5 mm×5 mm×1 mm的薄片，利用综合物性测量系统PPM叶蜡石热导率测试，同时利用LFA427激光热导仪测试数据对高温高压作用前后叶蜡石热导率作对比分析，此实验样品为直径10 mm、厚度1 mm的圆形薄片；在已知3组不同热导率基础上，结合本课题组对叶蜡石高温高压腔体不同区域XRD衍射分析相变物相的半定量计算结果[11]，计算高温高压后叶蜡石不同区域热导率值，结合相应组装材料的相关数据，利用有限元分析软件ANSYS，分别对片状触媒合成组装、直接加热及间接加热粉末触媒合成组装的3种组装方式合成腔体温度场进行计算机模拟分析。表1～表3分别为3种组装结构所用材料及规格，表4为所用材料性能参数。图1为腔体组装结构图。

表1 片状触媒组装结构材料规格 mm

表2 直接加热粉末触媒组装结构材料规格 mm

表3 间接加热粉末触媒组装结构材料规格 mm

2 结果与讨论

2.1 热导率实验测试结果分析及讨论

利用PPMS设备对高温高压合成金刚石后外层、中间层及内层3个区域叶蜡石热导率进行测试，结果如图2所示。由图2可得到高温高压合成金刚石后叶蜡石腔体不同区域热导率外层、中间层内层热导率分别为2.73、3.36、2.87 W/（m·K），其中中间层的热导率最大，内层次之，外层最小，这样的热导率分布可以使叶蜡石腔体的总散热量减少，叶蜡石的保温效果提高。

LFA427激光热导仪测试的高温高压前后叶蜡石热导率结果为：叶蜡石高温高压作用前的热导率测试值为6.48 W/（m·K），高温高压作用后叶蜡石热导率为2.78 W/（m·K）。结合图1结果我们发现，两种仪器测量的高温高压作用后叶蜡石热导率数据相近。

假设叶蜡石高压高温下无相变，且卸压后叶蜡石膨胀率等于保压过程中叶蜡石被压缩率，根据所测卸压后叶蜡石热导率数据来反推高压高温下叶蜡石受压缩时的热导率。以表面叶蜡石为例可得到高压高温下叶蜡石受压缩时热导率值为

6.48-2.98=x-6.48⇒x=9.98。

事实上，叶蜡石高压高温发生了相变，必须考虑叶蜡石相变对热导率的影响。根据对叶蜡石高温高压腔体不同区域XRD衍射分析相变物相的半定量计算结果[11]（如表5），计算了高温高压后叶蜡石不同区域热导率值，得到结果如下：

1） 外层：9.23×83%+8.38×17%=9.09 W/（m·K）；2）中间层：9.23×56%+8.38×36%+1.4×8%=8.30 W/（m·K）；3） 内层：9.23×59%+8.38×30%+1.4×(8%+3%)=8.11 W/（m·K）。

图1 腔体组装结构图

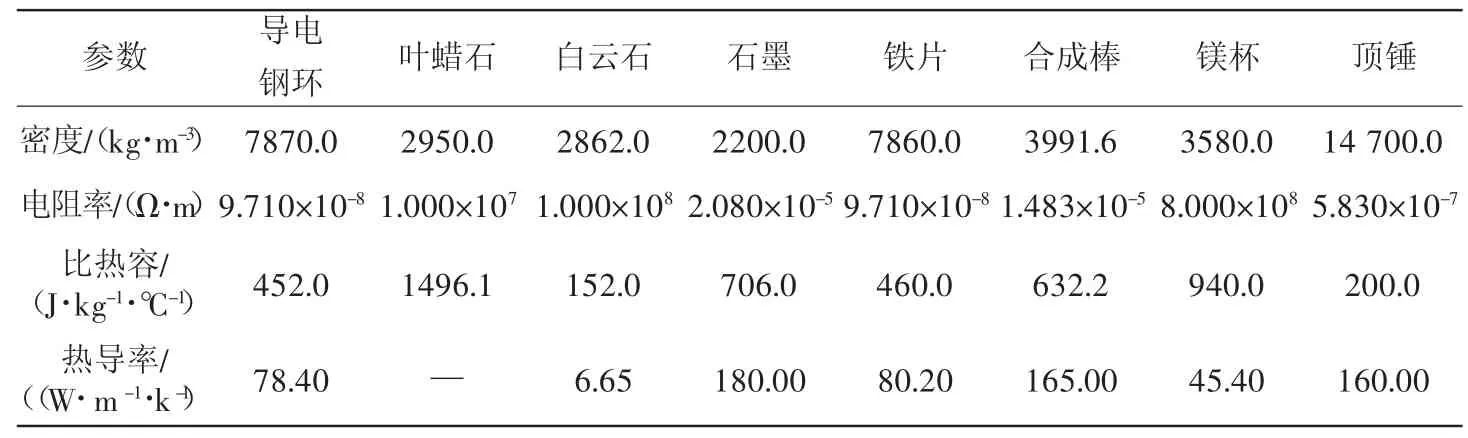
表4 材料性能参数

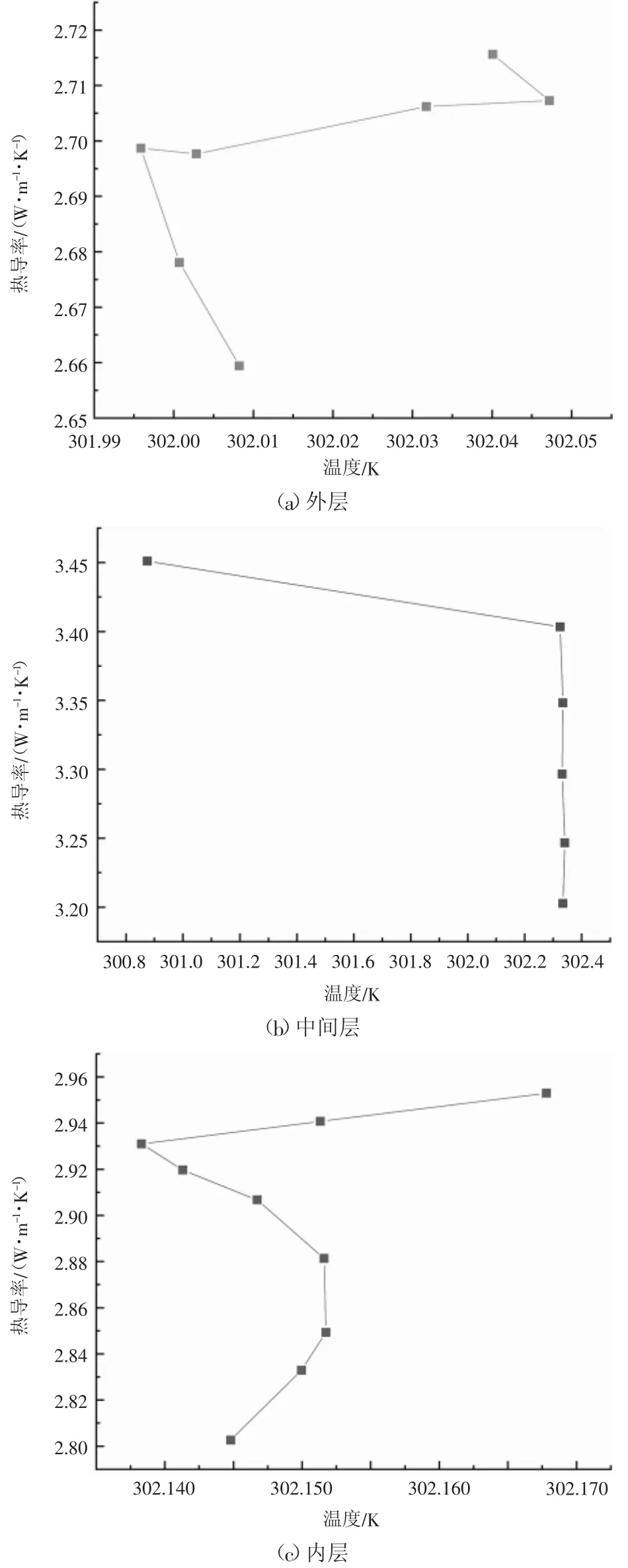
图2 叶蜡石不同区域热导率

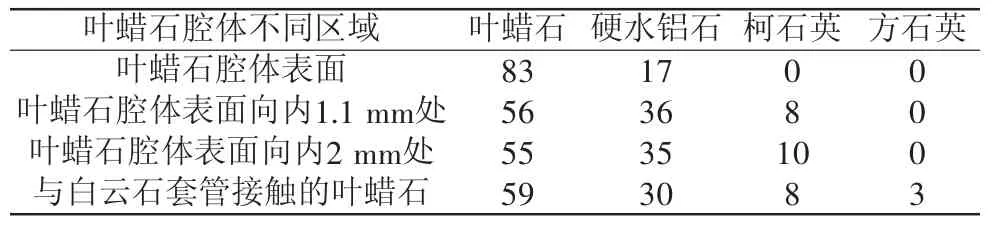
表5 叶蜡石高温高压腔体不同区域相结构各物相质量分数[11] %

2.2 叶蜡石高温高压腔体温度场模拟分析

第一套叶蜡石高压热导率数据，直接采用P. W.Bridgman[12]高压原位测试的结果，即热导率为9.23 W/（m·K)，并认为叶蜡石无相变，整个叶蜡石块热导率未发生变化，模拟计算得到温度场分布如图3所示。

第二套叶蜡石高压热导率数据，采用2.1小节中计算结果即外层为9.09 W/（m·K）、中间层为8.30 W/（m·K）、内 层 为8.11 W/（m·K），模拟计算得到温度场分布如图4所示。

图3（a）中心处片状触媒的温度区间在1256 ～1286 ℃之间，温差为30 ℃。图4（a）中心处片状触媒的温度区间在1315～1341 ℃之间，温差为26 ℃。从图3（a）、图4（a）可以看出，不同的导热系数对于合成腔体的温度场分布有很大的影响。已知NiMnCo触媒合成金刚石的最佳温度为1330 ℃左右，发现图3（a）所采用的数据模拟出的温度场与实际金刚石合成温度范围不一致，但图4（a）采用数据的模拟温度场与实际相一致，且越往端部温度越低，在边缘处金刚石生长得很少或质量变差，这与实际金刚石生长情况是一致的，因此我们认为运用第三种方法计算的叶蜡石的导热系数进行模拟更符合实际情况，得出的计算结果更精确。

由图3（b）可知，合成腔体中最高温度为1316 ℃，最低温度为1281 ℃，腔体内最大温差为35 ℃，径向最大温差为12 ℃，轴向最大温差为22 ℃。由图4（b）可知，合成腔体中最高温度为1336 ℃，最低温度为1302 ℃，腔体内最大温差为34 ℃，径向最大温差为12 ℃，轴向最大温差为25℃。对于图3（b）所示的温度场分布明显低于金刚石的实际合成温度，图4（b）中模拟计算温度场正好落在实际金刚石温度范围内，与实际合成金刚石情况相符，所以运用叶蜡石的此种导热系数进行模拟更符合实际情况，得出的结果更精确。同时我们通过模拟计算分析发现，虽然不同的导热率对模拟直接加热粉末触媒合成腔体温度场分布有很大影响，但是对于温度场中温差梯度影响不大，几乎不受影响。

图3 热导率取9.23 W/（m·K）时合成金刚石腔体温度场分布

由图3（c）可知，合成腔体中最高温度为1331 ℃，最低温度为1278℃，腔体内最大温差为53 ℃，腔体中心处径向温差为29℃，轴向温差为24 ℃。由图4（c）可知，合成腔体中最高温度为1356 ℃，最低温度为1301 ℃，腔体内最大温差为55 ℃，腔体中心处径向温差为33 ℃，轴向温差为22 ℃。同样，采用第一套叶蜡石导热率数据模拟计算的间接加热粉末触媒合成金刚石腔体温度场偏低，如 图3 （c）所示；按第三套叶蜡石导热率数据模拟计算的金刚石合成腔体温度场与实际金刚石的合成温度范围接近，如图4（c）所示，模拟结果与实际金刚石合成中温度场较为相符，说明运用叶蜡石的此种导热系数较为准确，所以准确输入高压下的叶蜡石物性参数，对于模拟计算结果的精确性尤为重要。

图4 热导率取相结构百分含量计算结果时合成金刚石腔体温度场分布

3 结论

1）采用综合物性测量系统PPMS分别测试了叶蜡石腔体不同区域的热导率，叶蜡石腔体从外到内的热导率分别为2.73、3.36、2.87 W/（m·K），与采用LFA427激光热导仪测试的高温高压作用后叶蜡石热导率2.78 W/（m·K）基本接近。

2）假设叶蜡石高压高温下无相变，且卸压后叶蜡石膨胀率等于保压过程中叶蜡石被压缩率，此时计算得到叶蜡石受压缩时热导率值为9.98 W/（m·K）。基于相变条件计算得到外层、中间层、内层热导率分别为9.09、8.30、8.11 W/（m·K）。

3）通过数值模拟分析发现不同的导热系数对于合成腔体的温度场分布有很大的影响。直接采用P. W.Bridgman高压原位测试的热导率9.23 W/（m·K）模拟的温度结果比实际温度偏低，通过腔体不同区域各相占的百分含量计算出的热导率模拟的结果与实际的温度分布更加接近。