大跨预应力混凝土斜拉桥平转施工阶段主梁受力研究*
2021-02-18郑建新孙南昌黄甘乐
于 哲,郑建新,孙南昌,黄甘乐
(1.中交第二公路勘察设计研究院有限公司,湖北 武汉 430056;2.中交第二航务工程局有限公司,湖北 武汉 430040;3.长大桥梁建设施工技术交通行业重点实验室,湖北 武汉 430040;4.交通运输行业交通基础设施智能制造技术研发中心,湖北 武汉 430040;5.中交公路长大桥建设国家工程研究中心有限公司,北京 100120)
1 工程概况
郑万高速铁路与郑西高速铁路夹角17°,采用(32+138+138+32)m斜拉桥转体跨越方案。斜拉桥为预应力混凝土结构,塔高86m,主梁平曲线半径1 400m,纵坡2.906 2%,采用箱形截面,宽11m。主梁现浇完成后,进行斜拉索架设,最后平转至设计目标位置。转体球铰设置在桥墩底部,竖向荷载16 500kN。桥型布置如图1所示,实景如图2所示。

图1 桥型布置(单位:m)

图2 转体前后实景
2 平转施工阶段主梁受力研究
根据速度变化情况,斜拉桥转体过程主要可分为启动、加速、匀速、减速和点动匹配5个阶段。桥梁平转施工风险高、控制难度大,通过对水平转体主梁进行有限元分析,研究不同角加速度对主梁受力的影响。在分析前,作如下假设:①假定转体施工在无风时进行,认为无风荷载作用;②在温度稳定的夜间进行,忽略环境温度影响,即认为平转施工中主梁顶底板的温度保持不变;③转体平顺无颠簸、转体系统及滑道等无异常;④将加速转体过程离散为多个不同的恒定加速度,不考虑连续变化影响。
2.1 主梁受力分析方法
根据理论力学,刚体绕转动轴(假设为z轴)的转动角动量可表示为:
(1)
式中:Mz为结构绕z轴转动的力矩;Lz为转动角动量;t为转动时间。
刚体转动角动量的表达式为:
Lz=Jω
(2)
式中:J为结构的转动惯量;ω为转动的角速度。
由式(1)、式(2)可得方程:
(3)
式中:α为结构转动的角加速度。
(4)
由加速转动引起的主梁应力为:
(5)
转体前应力水平σ0与惯性力引起的σω需满足:
σ0+σω<[σ]
(6)
式中:转动惯量J取值为1.32×109kg·m2;y为主梁断面外边缘与主梁转体中心的垂直距离,取值5.5m;I为主梁断面绕转动轴(z轴)的惯性矩,取值101.37m4。
由有限元模型计算得出,转体前根部梁段横断面A点为0.2MPa(受拉),B点为-0.3MPa(受压),以A点作为控制点(见图3),即σ0=0.2MPa。

图3 主梁横断面应力控制点(单位:cm)
在斜拉桥转体过程中,塔梁区梁段的受力最大,索塔处主梁根部的外边缘结构一侧受压、一侧受拉,根据相关规范,C55混凝土容许抗拉强度[σ]为1.89MPa(控制点A)。由式(6)求得此时转动角加速度为:
(7)
此时对应的根部梁段外边缘转动线加速度为0.13m/s2,B点应力为0.43MPa,表明以A点作为控制点合理。
2.2 有限元模型
采用有限元软件MIDAS/FEA建立空间实体模型(见图4),分析郑万高速铁路大跨曲线转体斜拉桥在加速转动过程中主梁的力学行为,有限元模型如图5所示。塔梁采用实体单元,斜拉索采用只受拉单元,塔梁固结,约束上转盘底部(桥墩底部)各节点的3个平动自由度,释放平转、竖转、扭转3个转动自由度,以此来模拟桥梁转体施工;其中主梁混凝土为C55,索塔混凝土为C50。

图4 有限元实体分析模型
在转体中,将[σ]作为控制条件,根据式(7)得到的计算结果,代入式(3)可得到对应的力矩荷载。假定主梁以下桥墩部分为刚体,忽略桥墩自身扭转变形效应,将力矩荷载施加到有限元模型的桥墩底部上,力矩荷载以节点荷载的方式施加,其作用点作为主节点,与周边节点形成主从刚性连接,以此来模拟角加速度对应的荷载,在转动力矩和自重作用下,结果如图5所示,塔根处梁段应力如图6所示。

图5 主梁应力分布

图6 塔根处主梁底板应力分布
在加速转动过程中,塔根处梁段应力呈S形对称分布(见图6)。由于主梁跨度较大,为长细比较大的构件,在加速转动时,主梁悬臂端的转动呈现“滞后”现象。即转盘带动桥塔转动,桥塔带动塔根处的主梁段,进而由塔根主梁段传递至主梁悬臂端。“滞后”效应使得塔根处主梁应力较大,在主梁全段范围内,该处成为最不利控制截面。
2.3 加速转动阶段主梁受力分析
在不同加速度情况下,由于斜拉桥为柔性高次超静定结构,基于恒定加速度分析方法未能考虑加速转动的连续变化过程,因此,选择主梁塔区梁段主梁外边缘转体线加速度<0.13m/s2,即对应角加速度为2.36×10-2rad/s2以下的一系列工况。
假定6种不同的加速度,取值依次为0.001,0.005,0.01,0.04,0.08,0.12m/s2,分别对应角加速度1.8×10-4,9.1×10-4,1.8×10-3,7.27×10-3,1.45×10-2,2.18×10-2rad/s2,根据式(3)可得到对应的力矩荷载,将其施加到桥墩底部处。对比这6种计算工况,确定合理的转速控制值。各工况结果如图7所示。
由图7可看出,在6种不同加速度转动情况下,塔根处主梁应力随着加速度的增大而增大,且增速越来越快,6种不同加速度工况下梁体所受到的最大拉应力如表1所示。

图7 不同角加速度下塔根处主梁受力

表1 不同加速度下梁体最大拉应力值
由表1可知,在0.001~0.01m/s2,塔根处主梁拉应力变化均在0.5MPa以内,应力变化较小,结构转动较安全。在实际转动过程中,由于转体自重较大,易造成不易控制的惯性作用,平转加速度控制在0.01m/s2(对应1.8×10-3rad/s2)以下,此时,桥体结构的转速变化率较小,转体施工较平顺,施工精度相对较高。
2.4 匀速转动阶段主梁受力分析
匀速转动在整个平转过程中持续时间最长,同样也是分析的重要环节,为了合理控制匀速阶段的转速,防止转速过大而发生失稳,有必要进行匀转动阶段主梁的受力分析。
分析匀速转动阶段作如下假设:忽略转体时大气温差的影响;假定转体过程平顺、无颠簸,转体系统无异常,忽略外界因素干扰,认为主梁转体保持均匀转动。
桥体转动的向心力公式为:
F=mRw2
(8)
式中:F为转动离心力;m为转体质量;R为质心与转动中心的距离。
在加速阶段,控制截面为主梁的塔根处,在匀速阶段,兼顾主梁悬臂端与塔根处的梁段应力分布,有限元模型采用0.01,0.05,0.1,0.5,1,2rad/min 6种计算工况,不同工况下梁体最大拉应力如图8及表2所示。

图8 不同转速下塔根处主梁受力
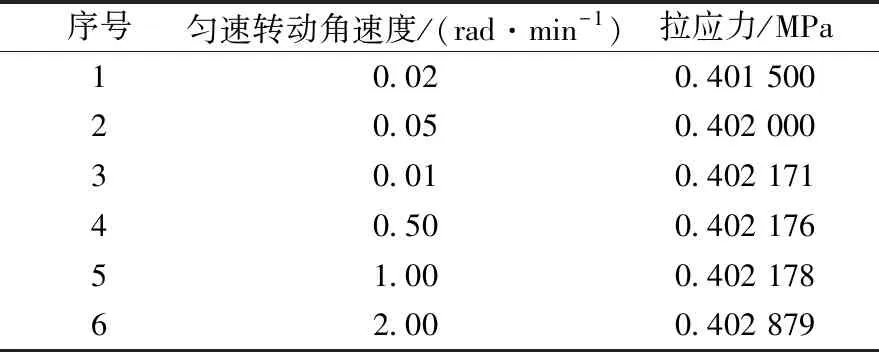
表2 不同转速下梁体最大拉应力值
在6种不同匀速转动的角速度下,主梁关键断面处应力变化不大,当以2rad/min匀速转动时,主梁拉应力达到0.403MPa。由以上分析可知,在0.01~2rad/min,主梁应力水平较稳定,变化不大。实际操作中,现场转速限定在0.02rad/min以内,此时桥体本身自重带来的惯性影响较小,且主梁应力较小,此时,匀速转动的安全性较高。
3 转速施工监测
3.1 转动速度监测
在监测实施中,桥梁转体角度由布置在上转盘的拉绳位移计进行监测,根据拉绳与转盘处的切线位移、切线速度可换算到转体角度、角速度等,传感器布置如图9所示。

图9 拉绳位移计布置示意
根据斜拉桥转体过程中的实测数据,整个转体过程共分37个转动阶段,其中1~6为加速阶段、7~29为匀速转动阶段、30~37为减速阶段及点动定位阶段,现场测试结果如图10所示。

图10 转动角速度测试结果
3.2 主梁受力监测
在梁体平转过程中,实时监测梁体应力变化,提取塔根处主梁断面随转体时间变化的应力监测值,对比情况如图11所示。
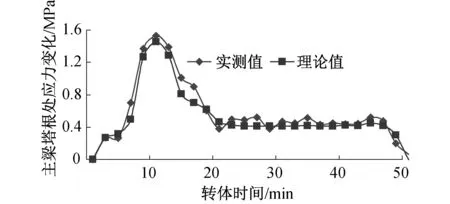
图11 主梁塔根处应力随转动时间变化曲线
由图11可知,在整个转体过程中,塔根处主梁应力变化呈现先增长后降低进而趋于稳定,最后降低至0的过程。在转体加速阶段,塔根处主梁应力达到峰值,随着加速度逐渐减小,应变变化开始缓慢降低;在匀速阶段,该处应力趋于稳定,应力变化实测结果与转动角速度相关性对应,且与理论分析误差在5%以内。
3.3 智能化监测平台
开发转体桥梁智能化监测平台(见图12),实时监控桥梁线形、空间位置、线形及应力,通过实时监测转体状态,根据不同转体阶段的控制条件进行远程调控,确保主梁转体平稳、控制精准,并对异常情况及时做出预警。

图12 三维智能化监测平台
4 结语
1)曲线斜拉桥主梁的长细比较大,在加速过程中,由于主梁悬臂端的运动存在滞后效应,导致塔根处梁段应力呈S形分布,为受力最不利区域。
2)在加速阶段,塔根处主梁应力变化较大,当主梁根部断面外边缘线加速度达到0.13m/s2时,根部梁段拉应力接近抗拉强度设计值;当控制在0.01m/s2以内时,转体平稳、安全。
3)在匀速阶段,主梁应力变化微小,在0.02rad/min以下时,转速影响可忽略。
4)塔根处梁段应力理论值与实测值误差在5%以内,验证了平转主梁受力特性。
5)桥梁智能自适应转体控制系统研发及应用,完成了“小天窗、高效率”智能连续转体,三维可视化控制平台实现了转体桥梁的精准控制。
