基于天线扫描的雷达成像方法

丁 斌，夏 雪

(1.西安文理学院，陕西 西安710065；2. 西安卫星遥感服务中心，陕西 西安710065；3. 西安石油大学，陕西 西安710065)

0 引言

合成孔径雷达(synthetic aperture radar, SAR)已广泛应用于国土测绘、灾害预防与评估、导航与制导等军用和民用领域，大大提高了人们对信息的获取与感知能力。SAR在方位向依靠雷达平台运动，等效地在空间形成较长的合成孔径，获得方位高分辨率。SAR提高方位分辨率的前提条件是目标和雷达有相对运动，而且雷达到目标的连线与相对运动轨迹之间要有一定的角度约束[1]。这就使得SAR在实际应用中受到一定限制，例如在某些情况下需要对雷达正前方目标进行成像时，SAR就不能对正前方目标形成合成孔径了[2]。除了合成孔径技术外，国内外学者对提高雷达方位分辨率的其他方法开展了广泛深入的研究。

文献[1—2]提出了单脉冲成像算法，该类算法的基本思想是利用足够高的距离分辨率分辨出目标上的主要散射体，然后利用单脉冲测角技术获得散射点偏离波束中心的角度，进而对目标进行定位。尽管单脉冲测角在理论上具有很高的测量精度，但对于复杂目标相对天线波束运动时，会引起目标视在中心与目标实际中心的偏离，产生角闪烁现象，使得测量精度大大下降。文献[3—5]提出了基于反卷积提高雷达的角分辨率算法，这类算法的核心思想是基于雷达回波是天线方向图与目标方位位置的卷积结果，使用已知的天线方向图对雷达回波进行反卷积，就能反演出目标的方位位置；然而，由于雷达回波中存在杂波、干扰和噪声，这就严重影响了反卷积的结果。此外进行反卷积时，天线方向图的截断也会影响反卷积结果。文献[6]提出利用广义逆滤波方法在低信噪比条件下，可有效改善实孔径雷达的角分辨率，但时域计算较为复杂。文献[7—9]研究了维纳逆滤波算法，在回波信噪比较高的情况下，该方法可实现方位高分辨。文献[10]使用范数正则化方法来求解在低信噪比条件下的雷达方位超分辨问题。针对合成孔径雷达成像时需要雷达或目标运动，且存在成像盲区的问题，提出基于天线扫描的雷达成像方法。

1 基于天线波束扫描的雷达成像几何模型

基于天线波束角度扫描的雷达成像几何模型如图1所示。

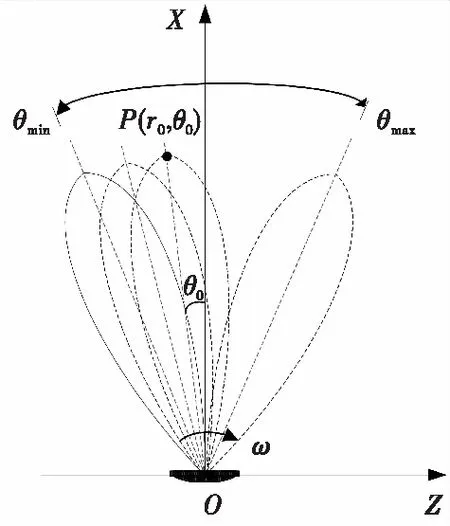
图1 基于天线波束角度扫描的雷达成像几何模型Fig.1 Geometric model of radar imaging based on antenna beam angle scanning

设雷达天线相位中心位于坐标原点O，点目标P与原点O相距r0，点目标P的方位向角度为θ0。天线波束在方位向以角速度ω，沿顺时针方向，从角度θmin扫描至θmax。假定点目标P固定不动，随着天线波束的扫描，点目标P从波束前沿进入天线波束，从波束后沿划出。设天线波束的主瓣(也就是3 dB波束宽度)为θ3 dB，点目标P在θ3 dB内的驻留时间为Tscan，则有：

(1)

设雷达脉冲重复时间(PRT)为T，则点目标P在θ3 dB驻留时间内，发射、接收的回波脉冲数N可表示为：

(2)

如前所述，在天线波束扫描过程中，当波束主瓣的前沿到达点目标P时，脉冲压缩编码就开始对雷达发射信号进行编码(调制)。波束在θ3 dB范围内扫描时，编码也相应变化。直到波束后沿到达点目标P时，完成最后一个(即第N个)脉冲压缩编码。这里假定雷达信号为线性调频信号，则点目标P的雷达回波信号可表示为：

(3)

式(3)中，tr为距离向时间，即“快时间”；ta为天线波束角度扫描时间，即“慢时间”；G2(·)为ta时刻目标角度位置对应的天线增益(双程)；c为电磁波传播速度；Kr为线性调频信号(linear frequency modulation, LFM)信号的调频率；Ck(·)为波束在θ3 dB内扫描时，同步脉冲压缩编码调制信号。这里的脉冲压缩编码调制信号可以是调相信号(如相位编码信号)也可以是调频信号(如LFM信号)。携带了同一脉冲压缩编码信号的雷达发射信号与点目标P作用后返回被雷达接收。点目标P在θ3 dB驻留时间内的波束扫描角度与脉冲压缩编码调制信号是一一对应的，即脉冲压缩编码是波束扫描角度的函数。

当然上述回波产生过程是针对单个点目标来说的，对于面目标回波生成过程如下：为了便于说明，在天线波束扫描过程中，只考虑同一距离单元内，方位向天线3 dB波束范围内的区域。当波束前沿扫瞄到该区域头部时，慢时间脉冲压缩编码开始对雷达信号进行编码调制。在波束方位向扫描过程中，编码也相应变化(编码是方位扫描角度的函数)，直到天线波束扫描到该区域的尾部，完成最后一个脉冲压缩编码。

2 基于天线扫描的雷达成像方法

基于天线波束扫描的雷达成像处理流程如下：

1) 距离维脉冲压缩

点目标P的回波信号，经过距离维脉压处理后，得到：

(4)

式(4)中，A为距离向脉压后点目标P的幅度，B为LFM信号的带宽。可见，点目标P的N个脉冲回波经过距离脉压后，是N个在方位向分别被脉冲压缩编码和天线方向图调制的“辛克”函数。脉冲压缩编码与天线扫描角度(θ3 dB范围内)是一一对应的。

2) 方位角度维脉冲压缩

在波束角度扫描过程中，对雷达发射信号同步进行脉冲压缩编码调制，天线主瓣就相当于一个“角脉冲”，“角脉冲”对应的时宽等于天线扫描一个主瓣宽度所需时间。

具体到点目标P的回波，“角脉冲”的时间宽度为：

Tscan=N·T

(5)

式(5)中，T为脉冲重复时间间隔，即子脉冲时宽，也就是波束扫描一个角度步进所用时间。角脉冲经过匹配滤波后，其信号能量被压缩在角脉冲中某个子脉冲宽度内，子脉冲对应的天线扫描角度就是点目标P的方位角度。角度维脉压后的角度分辨率可表示为：

ρa=ω·T

(6)

由式(1)、式(5)和式(6)可得：

(7)

同距离维匹配滤波一样，在方位角度维，通过角脉冲的脉压处理可以将雷达的方位角分辨率从θ3 dB提高到θ3 dB/N。由式(7)可见，决定角分辨率的因素是天线主瓣宽度θ3 dB和角脉冲内的子脉冲个数N。

下面以二相编码调制为例，对方位角度维脉压处理的解析表达式进行推导，使用角度扫描子脉冲持续时间T和脉冲截止时间ε来表示角度扫描时间ta，即：

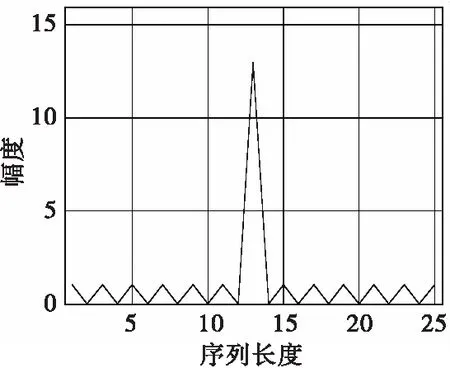
ta=k·T+ε,0<ε

(8)

则经过角脉冲匹配滤波处理可得：

(9)

式(9)中，A1为考虑天线方向图幅度加权和两维脉压后的幅度值，x[k]为二相码序列的离散自相关。

式(9)给出了在ta=KT时刻的x[k]的函数，该函数在相邻的采样值x[k]和x[k+1]之间进行线性插值(在复平面内)，因此，通过计算多项码序列幅度自相关，并在这些值间进行线性插值，即可以得到其匹配滤波器输出。以13位巴克码序列为例，它的自相关函数见图2所示。

图2 13位巴克码序列自相关函数Fig.2 Autocorrelation function of 13 bit Barker code sequence

可见，通过在距离和方位角度维分别进行脉冲压缩，就能对目标进行二维(距离-方位角度维)成像，整个成像处理流程如图3所示。

图3 算法流程图Fig.3 Flow chart of the algorithm

3 仿真实验

假设雷达系统发射信号为LFM信号，雷达系统参数如表1所示。天线波束扫描过程中，使用13位巴克码序列同步对雷达发射信号进行脉冲压缩编码，分别在信噪比为0、10、20、30 dB和没有噪声情况下，对点阵目标进行成像处理。设置的点阵目标(共5个点目标)位置如图4所示。

表1 雷达系统参数Tab.1 Radar system parameters

如图4所示，用于仿真的共有5个目标点，其中点目标1、2和4摆放在同一方位向角度，距离向间距为100 m，点目标3、4和5摆放在同一距离向，方位向角度间隔为0.6°。

图4 仿真中点阵目标位置Fig.4 Position of point array targets in simulation

在没有噪声的理想情况下，点阵目标距离维脉压结果如图5所示，可见目标点的方位角度分辨率为3.9°，即仿真中天线方位向3 dB波束宽度，也就是实孔径角分辨率(这里将距离维脉压结果简记为实孔径结果)，而方位角度间隔0.6°的点目标3、4和5在方位角度维不可分辨。

图5 点阵目标距离维脉压结果(实孔径)Fig.5 Range dimension pulse compression result of point array targets (real aperture)

在没有噪声情况下，图4中点阵目标回波经过距离维和方位角度维脉压处理后的结果如图6所示。可见经过方位角度维脉压处理后，点阵目标的角分辨率得到显著提高，点目标3、4和5在图6中可以分辨。

图6 点阵目标成像结果Fig.6 Imaging results of point array targets

在信噪比为0、10、20、30 dB情况下，对图4中点阵目标进行成像处理，信噪比为0 dB的成像结果如图7所示(这里限于篇幅，只给出了信噪比为0 dB的成像结果)。

图7 信噪比为0 dB时点阵成像结果Fig.7 Imaging result of point array targets (SNR=0 dB)

对比图6和图7可知，尽管在信噪比为0 dB情况下，点阵目标的方位分辨率几乎没有降低。点目标1和2的成像质量如表2和表3所示。

表2 不同信噪比时目标点1方位角度维聚焦质量Tab.2 Compression performance of target 1 in azimuth angle dimension at different SNR

表3 不同信噪比时目标点2方位角度维聚焦质量Tab.3 Compression performance of target 2 in azimuth angle dimension at different SNR

由表2和表3可见，点目标1和2的方位角度分辨率均可达0.26°左右，仿真结果优于理论分辨率0.3°，这是因为在仿真中考虑了双程天线方向图幅度加权因素。可见，本文提出的角脉冲压缩算法可将雷达的方位分辨率提高15倍左右；从峰值旁瓣比和积分旁瓣比两个指标来看，在方位角度维也能获得较好的聚焦性能。此外，随着信噪比的降低，点目标1和2的方位角度分辨率和聚焦性能略有下降，但是下降程度微小。可见，角脉冲压缩技术在低信噪比情况下，依然能提高角度分辨率。

不同信噪比条件下，点目标3、4、5的方位角度维脉冲响应函数，如图8所示。

图8 不同信噪比时三点目标方位角度维脉冲响应函数Fig.8 Impulse response function of three point targets in azimuth angle dimension t with different SNR

由图8可见，随着信噪比的降低，3点目标的方位角度维脉冲响应函数有所恶化，主要表现为：主瓣略微展宽，旁瓣幅度也有所抬高；但是脉冲响应函数的恶化程度很小，不影响雷达对目标的分辨。由雷达分辨理论和模糊函数理论可知[11]，信号+噪声的功率谱完全决定了脉冲响应函数的主瓣宽度。当随着信噪比的降低，即噪声增强，噪声的功率谱幅度也随之增强，进而使脉冲响应函数输出主瓣展宽。

设信号为s(n)，噪声为g(n)，雷达回波信号为x，则有：

x(n)=s(n)+g(n)

x(n)的功率谱为：

X(f)=S(f)+G(f)

G(f)的形状会叠加到S(f)上，构成X(f)的频率结构，从而影响脉冲响应函数主瓣宽度的大小。

同时x经过脉冲压缩后的归一化输出包络可表示为：

(10)

式(10)中，分母表示主瓣峰值，分子是未归一化的值，包含加权后信号的固有旁瓣成分和噪声成分。可见旁瓣将伴随着信噪比的降低而增大。

此外，与实孔径结果相比，尽管在低信噪比情况下，本文方法也能提高方位角度分辨率，角度分辨率提高约15倍左右。

在仿真中使用13位巴克码序列对雷达发射信号进行脉冲压缩编码。在实际中如果需要更高的角度分辨率，可以根据式(2)计算所需要的码序列的位数，使用相应位数的码序列编码调制。

4 结论

本文提出一种基于天线扫描的雷达成像方法。该方法通过在天线波束角度扫描过程中，对雷达发射信号进行脉冲压缩编码调制，编码调制与波束角度扫描同步进行，进而在波束扫描角度维进行脉冲压缩，提高雷达的角度分辨率；同时利用宽带信号提高距离维分辨率，获得目标两维高分辨率(距离维和角度维)雷达图像。仿真结果表明所提方法较传统SAR成像方法，对正前视目标具有更高的方位分辨率。