关于插入排序的分析及构想

颜文岩 刘朝元 吴彩莲

摘要：在排序中分为内排序和外排序，而我们今天要做的插入排序在排序过程中，整个表都放在内存中处理，排序时不涉及数据内存与外存之间的交换，因此也被称为内排序。插入排序的基本思想是每次将一个待排序的元素按其关键字大小插入到前面已经排好序的子表中的适当位置，直到全部元素插入完为止。

插入排序的分类

插入排序的方法非常之多，今天我们主要研究这三种：

第一种：直接插入排序;

第二种：折半插入排序;

第三种：希尔排序;

...

直接插入排序

假使我们将所有待排序的元素放在一个一维数组a[]中，那么在排序过程中会产生两个区域。一部分是已经经过直接插入排序的区域，该部分区域内的元素有序排列，但相对于整体来说只能认为是局部有序;另一部分是还未进行排序的区域，该部分区域内的元素无序排列。这种方法也被叫做增量发，它使有序区每次增加一个元素，只有当最后一个元素也进行排序后整个数组才是全局有序的。

但是由于直接插入排序是每一个元素都要与之前进入有序区的元素进行比较，随着有序区元素的增多，计算量也在不断的增大。算法的最小时间复杂度为O（n），算法的最大时间复杂度为O（n2），算法的平均时间复杂度为O（n2）

但值得一提的是——直接插入排序算法中只使用了三个辅助变量因此可以说是一个就地排序算法。

折半插入排序

与直接插入排序一样，折半插入排序也是将所有数据放入一个一维数组a[]中，并在排序过程中将所有元素分为有序区与无序区。但与之区别的是，在程序运行过程中无序区被选中排序b的元素在进入有序区进行排序时并不是一个接一个进行顺序比较。而是，因为有序区的元素都是局部有序的，所以b与有序区的中间位置的元素也就是此部分的中位数c进行比较，来决定下一个比较的对象是在c的左侧还是右侧，这种方法与二叉树排序的思想非常相似所以也被称为二分插入排序。

实际上，折半插入排序和直接插入排序比较来看，需要移动的元素并没有减少，的但这并不是说折半插入排序和直接插入排序就可以画等号。

就事实而言，折半插入排序的平均时间复杂度也为O（n2），但是折半查找时的比较次是直接顺序比较的一半，尽管折半插入排序也属于直接插入排序，折半插入排序的空间复杂程度为O（1），但是性能要优于直接插入查找。

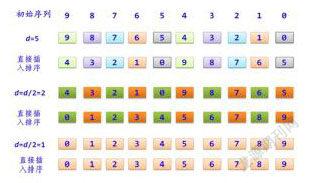
希尔排序

希尔排序尽管也是一种插入排序，并且也用了数组的思想。但是不是在一维数组是而是二维数组，并且对所有元素金星分组插入。其具体操作方法为——建立设一个a[i][j]。i表示所分的组，j是每个组内的元素个数。

在每一个小分组内，元素的排序是按照直接插入排序使每个分组局部有序，所以要想所有的元素全部有序，就需要不断的重复上述操作，并且将组数减少，使每个组内的元素逐渐增多，每一次都对其重新排序。直到将二维数组转变为一维数组，这时进行最后一次组内排序后，整体变为有序数组。

因此，希尔排序也被称为减少增量的排序方法，在希尔排序每趟完成后数据越来越接近有序。

希尔排序的平均时间复杂度为O（n1.3），从平均时间复杂度上就可以直观的看出希尔排序要远远优于直接插入排序和折半插入排序。但当增量为一时，希尔排序与直接插入排序基本一致，但希尔排序在效率上较直接插入排序在效率上更加简洁高效，并且减少了时空开销，大大减少了计算机的运算负担。

自我分析

在看完上述这三个经典的案例之后，有没有一个想法，那就是直接插入排序、折半插入排序还有折半查入排序能否在进一步优化呢？答案是肯定的。所以我在想如果有n個元素那么必然有两种情况：第一种，这n个元素是连续的;第二种，这n个元素不是连续的。

当n个元素连续时，我们不妨将n个元素放入一个a[m][n]的二维数组中，并在定义一个空的大小一样的二维数组。第一步，将数组的每一行进行从小到大直接排列;第二步，将所有的每一行的最小元素与最大元素分别放进定义的min[]和max[]，第三部，找出min[m]中最小的将它所在的行与第m=0行交换，找出max[m]中最大的将它所在的行与第m=m行交换，前提是这来两个元素不在同一行，如果在同一行将啊a[m][0]与a[m][n]交换。第四步，将a[0][0]/n==ys，将判断a[m][n]-a[0][0]是否等于n-1;如果是，那么这组元素就是连续的，如果否。当为是时，将原来a[m][n]中的每一个元素除以n再减去ys得到元素行号，并将之顺序放入。第五步，全部放入后在进行一次行内排序，整个数组就变为有序的了。当为否时，运用希尔排序。在这种方法下，如果元素是连续的那么平均时间复杂度为O（n），因此，也可以在一定的方式下加快运算的速率。

那么在这时最大的问题就是如何进行分组，当数据过大时分组的组数就成了一个尤为头疼的问题，以2进制来看，找到一个2n最接近元素个数的数，以n作为组数。

总结

内排序是快速搜索的重要一环，因为内存的运算速度快造价高昂，决定了他的存储容量不可能想外存那样大，所以为了不造成计算机运行的拥堵，内存必须保持一定的容量，这时候时间复杂度与运算的时间就显得尤为重要。早一点完成就可以早一点转出内存，腾出更多的空间，使计算机更加流畅。

数据如果在使用的时候是无序的，在使用时查找起来会花费大量的时间，降低用户体验，随着现在数据传输速率的加快也更容易造成卡顿。

参考文献

《数据结构教程（第5版）》李春葆

《插入排序法研究（1）》唐开山

《数据结构与算法详解》陈锐