基于FOA-MCB的无线传感器网络节点定位精度分析

张晓玲，商迎美，陈自红

(安徽三联学院 1.机器人工程学院；2.科研处，安徽 合肥 230601)

随着现代科技的发展，无线传感器网络(Wireless Sensor Networks, WSN)被大量使用，其能够实时监测环境中温度、风速等信息[1-2]。无线传感器网络的使用成本较低，组网效率快，在灾难援救、医疗领域等较为常用[3]。节点定位方法在无线传感器网络中占据十分重要的地位，在环境探测问题中，高精度定位森林温度异常点属于火灾防治的必要条件[4]。在商业领域中，无线传感器网络节点定位能够准确定位养老院病人的所在位置。在军事领域中，无线传感器网络节点定位可准确提取入侵人士的所在位置[5]。基于此，无线传感器的网络节点能够准确定位非常重要。

在无线传感器网络实际使用中，GPS定位较为常用，而传感器节点具有海量性，分布状态不具有规律性，从传感器与GPS的体积、功能以及应用环境等角度分析，对每一个无线传感器网络节点都安置一个GPS并不可能实现。所以，高精度的无线传感器网络节点定位方法是目前无线传感器网络研究人员的热点研究问题[6]。

目前很多定位方法虽然定位精度均较高，但是，计算开销也较大。无线传感器网络中，用来描述定位误差的指标大多以距离误差均值、定位误差均值为主[7]。但根据相关研究表示，节点的定位精度不光和定位方法有关，还与定位节点所靠近的锚节点几何布局存在密不可分的关系。锚节点几何布局出现变动，对节点定位精度存在一定影响，所以，为了提升无线传感器网络节点定位精度，需要分析定位精度和锚节点几何拓扑之间的关联性。本文提出基于FOA-MCB算法的无线传感器网络节点定位精度分析方法，在使用基于FOA-MCB算法的无线传感器网络节点定位方法，定位无线传感器网络节点之后，引入定位精度的几何稀释(GDOP)来分析无线传感器网络节点定位精度。

1 基于FOA-MCB算法的无线传感器网络节点定位精度分析方法

1.1 基于FOA-MCB算法的无线传感器网络节点定位方法

1.1.1 果蝇优化算法

果蝇拥有其他动物并不拥有的灵敏嗅觉与视觉，果蝇可以闻到大于10公里的食物味道，并使用嗅觉检索目标味道所在的具体方位，果蝇优化难度较小，收敛效率显著[8-9]。

果蝇优化方法的步骤如下。

第一步骤：初始化参数。

果蝇群体方位坐标是(xa,ya)，个体数量为M，迭代次数最大值是Fmax，检索步长是k。

第二步骤：计算果蝇搜索食物的飞行距离，计算公式如式(1)所示。

(1)

其中，Xo、Yo分别是飞行距离中的横纵坐标位移值。

基于此，果蝇搜索食物的飞行距离总值E(i)计算公式如式(2)所示。

(2)

第三步骤：计算果蝇味道浓度判断值R(i)，计算公式如式(3)所示。

(3)

第四步骤：为了计算各个果蝇个体的适应度值G(i)，需要导入适应度函数Function，如式(4)所示。

G(i)=Function(R(i))

(4)

第五步骤：提取果蝇群体里适应度函数最大或最小的果蝇个体bs、bd，如式(5)所示。

[bs,bd]=[max(G(i)),min(G(i))]

(5)

第六步骤：记载最大适应度值和最优果蝇坐标，剩下果蝇个体向此最优位置的方向飞行，其计算公式如式(6)所示。

(6)

其中，xa、ya依次是果蝇个体飞行到最佳位置距离的横纵坐标位移值，X(bs)、Y(bs)依次是具有最优适应度值和最优果蝇个体的坐标。

第七步骤：迭代寻优。

迭代寻优后，循环第二步骤至第五步骤，判断各次迭代中，所有果蝇个体是否都向最优位置的方向飞行，若是，便跳回第六步骤，反之继续循环迭代。

上述过程中，搜索步长k十分重要，对搜索效率存在直接影响，应将搜索步长重点考虑。为将果蝇优化算法与无线传感网络节点定位相结合，本文把k变换为Δt×uj(t)，则：

(7)

其中，Δt代表单位时间，uj(t)代表果蝇飞行的速率。

果蝇算法优化适应度函数可优化无线传感网络的定位精度，所以必须使用存在节点位置指标的函数g(Function)，当果蝇优化算法使用在无线传感网络节点定位问题中时，各个果蝇个体表示一个网络节点j，估计位置是Aj=(xj,yj)，各个果蝇需要使用式(7)更新自身位置。

定位无线传感器网络节点定位时，锚节点十分关键。锚节点又称信标节点，可作为节点定位中的参考节点，为需要定位的节点提供参考坐标。假设在定位范围中具有n个锚节点，设锚节点坐标Ci=(xi,yi)，那么t时间段中需定位节点j与锚节点i之间的预计距离是：

(8)

设Hji是t时间段中网络节点j与锚节点i之间实际距离，根据两节点间的预计距离和实际距离，获取果蝇优化算法的适应度函数如式(9)所示：

g(x,y)=Eji-Hji

(9)

1.1.2 FOA-MCB定位算法的实现步骤

本文采用FOA-MCB定位算法进行网络节点的定位，其实现步骤如下所示。

(1)初始化，设置果蝇个体的速度与位置。

(2)使用MCB定位算法，定位无线传感器网络中需要定位的节点位置坐标，定位方法如下。

①无线传感器网络锚节点i在无线传感器网络中明示自己的位置坐标(xi,yi)。

②若无线传感器网络中需定位节点j检测到多个和自己通信的锚节点位置，使用锚节点建立锚盒，在采样盒中任意建立M个样本个体，各个样本表示节点在某方位的可能性。

③若无线传感器网络中需定位节点j检测发现某个和自己通信的锚节点信息，便运算各个网络节点样本个体和锚节点之间的欧式距离，之后取出欧式距离较大的样本并舍弃，对有效样本个体设置权重[10]。

④多次执行①-③步骤，如果得到的有效样本数量不符合条件，便循环采样并过滤，直至满足样本数量要求。

⑤t时间段无线传感器网络中需定位节点的估计位置坐标主要通过样本点的加权均值获取[11-12]。

(3)计算各个果蝇个体和锚节点的距离，并计算各个果蝇适应度值。

(4)计算各个果蝇个体最优位置坐标。

(5)分辨各个果蝇个体的适应度值是否比上一代优越，如果是，记载最优个体位置，更新各个个体的位置[13]。

(6)迭代次数未达到最大值时，跳转至第(3)步骤再次循环操作，反之，把目前最优果蝇个体位置设成无线传感器网络中需定位节点位置的最优解。

1.2 基于GDOP值的无线传感器节点定位精度分析方法

结合上文方法可知，锚节点几何布局对无线传感器节点定位精度存在一定影响，为了准确分析无线传感器节点定位精度和锚节点几何布局的关系，本文使用几何稀释GDOP值分析此问题[14]。

设置GDOP是：

(10)

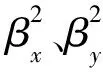
设置Δβ是无线传感器节点位置Pj和定位值Aj之间差值矢量，c1,c2,…,cj是无线传感器节点指向每个锚节点的单位矢量，则：

(11)

其中，Tnj是第j个锚节点到目标节点的时间；sj是第j个锚节点到目标节点的距离；T0是锚节点发送信号时间；d是信号的传播速度；δj、εj依次是误差矢量与误差矢量的均值。εj和Δβ的矢量关系如图1所示。

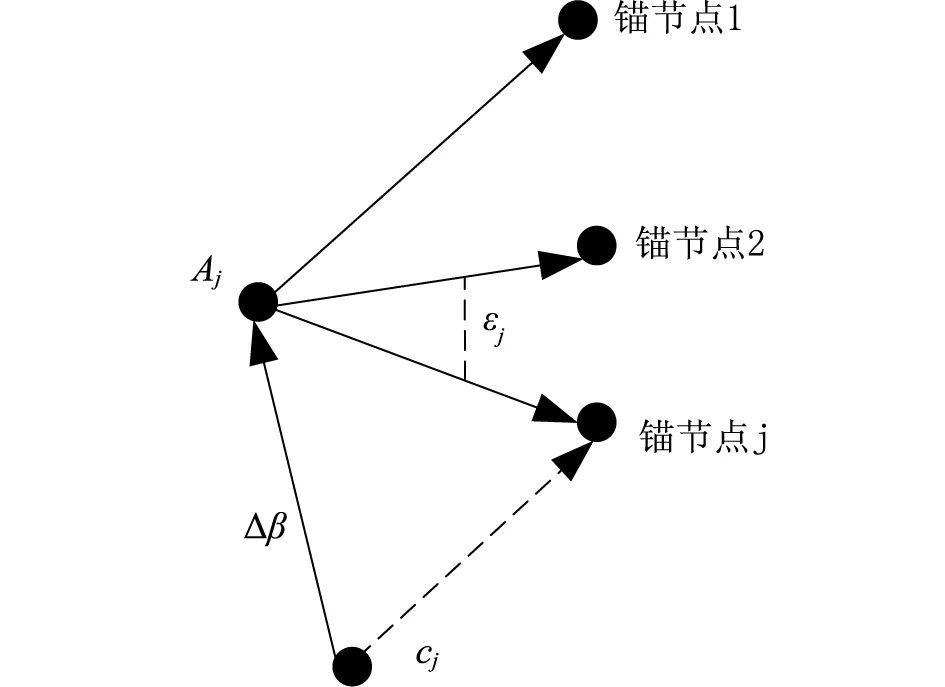
图1 εj和Δβ的矢量关系

无线传感器节点定位的时差值测量方程是：

tnj-tnj+1=(εj-εj+1)/d+

(cj-cj+1)·Δβ/d+(δj-δj+1)

(12)

时差值矢量矩阵设成：

(13)

其中，Tn=[tn1,tn2,…,tnj]T，上标T代表转置；δ=[δ1,δ2,…,δj]T；ε=[ε1,ε2,…,εj]T；G=[G1,G2,…,Gj]T，G是梯度值。

(14)

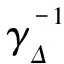
(15)

将协方差变换为式(16)：

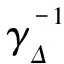
(16)

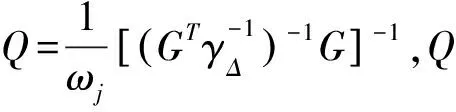
此时归一化的GDOP是：

(17)

其中，Qxx、Qyy是在x轴、y轴中因均方根测距误差、因集合关系而变动的无线传感器节点定位误差放大系数。

2 实验分析

2.1 实验设置

在100mm×100mm范围中设置多个传感器节点，建立一个无线传感器网络，其结构如图2所示。设置锚节点与常规节点的通信半径均为55mm，将无线传感器网络中需定位节点的定位值和实际值之间归一化的GDOP值设成性能测试指标。

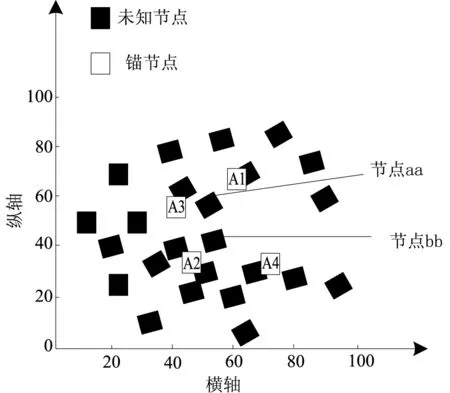
图2 无线传感器网络结构

图2中，位置节点aa、bb能够通过锚节点A1、A2、A3、A4锚节点判断位置。锚节点A1、A2、A3或A2、A3、A4都可以对无线传感器网络中需定位节点bb的位置进行定位。在以节点bb为坐标原点的坐标系里，运算锚节点A1、A2、A3或A2、A3、A4的(GDOP)m值。使用3个锚点组合形式，对无线传感器网络中需定位节点bb实施节点定位时，节点bb处于锚点A2、A3、A4区间中，在锚节点A1、A2、A3区间外。无线传感器网络中需定位节点的定位结果即为区间中的质心，如果节点bb与此区间的质心十分靠近，无线传感器网络中需定位节点定位精度便较为显著。根据此类标准，锚节点集合和需定位节点的几何布局存在两种情况。

(1)需定位节点出现在锚节点环绕的区间中，简称为锚节点群内点。

(2)需定位节点未出现在锚节点环绕的区间中，简称为锚节点群外点。

2.2 锚节点位置对节点定位精度的影响

使用本文方法分析无线传感器网络节点定位精度时，测试本文所提定位方法对无线传感器网络节点精度，将测试次数设成200次，锚节点数量是3个，求解锚节点群内点、外点的需定位节点定位精度归一化GDOP值，求解结果如图3所示。

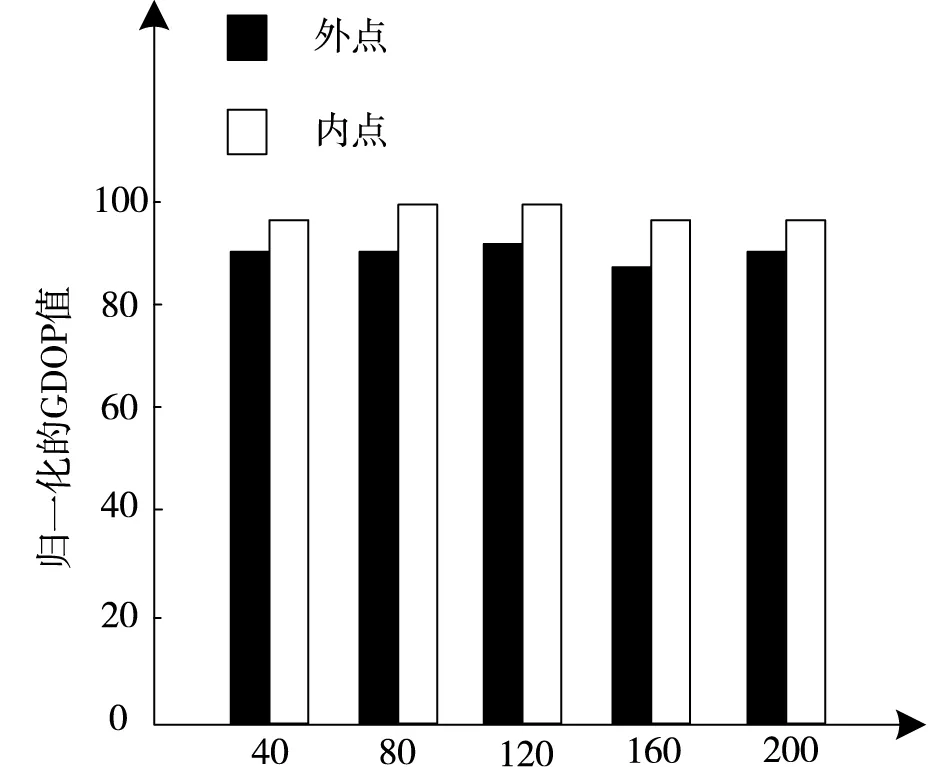
图3 内外点归一化GDOP值

由图3可知，采用本文方法分析后可知，无线传感器网络节点定位后，内外点归一化GDOP值显示，内点定位精度大于外点定位精度。实际定位中，为了减少通信与运算损耗，一般会选取3个锚节点对需定位节点实施定位，锚节点的几何布局对定位精度存在直接影响，以节点bb为例，节点bb属于A2、A3、A4内点，能够提升无线传感器网络中需定位节点定位精度，A2、A3、A4是节点bb最合适的几何布局。由此可见，锚节点的位置对无线传感器网络节点定位精度存在直接影响。

2.3 锚节点数量对节点定位精度的影响

无线传感器网络中，锚节点的数量对无线传感器网络定位精度也存在影响，设置锚节点分别是3个与4个，在此条件下，使用本文方法求解锚节点群内点、外点的需定位节点定位精度归一化GDOP值，求解结果如图4所示。

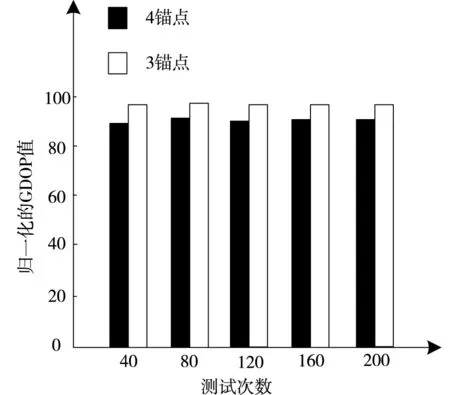
(a)内点

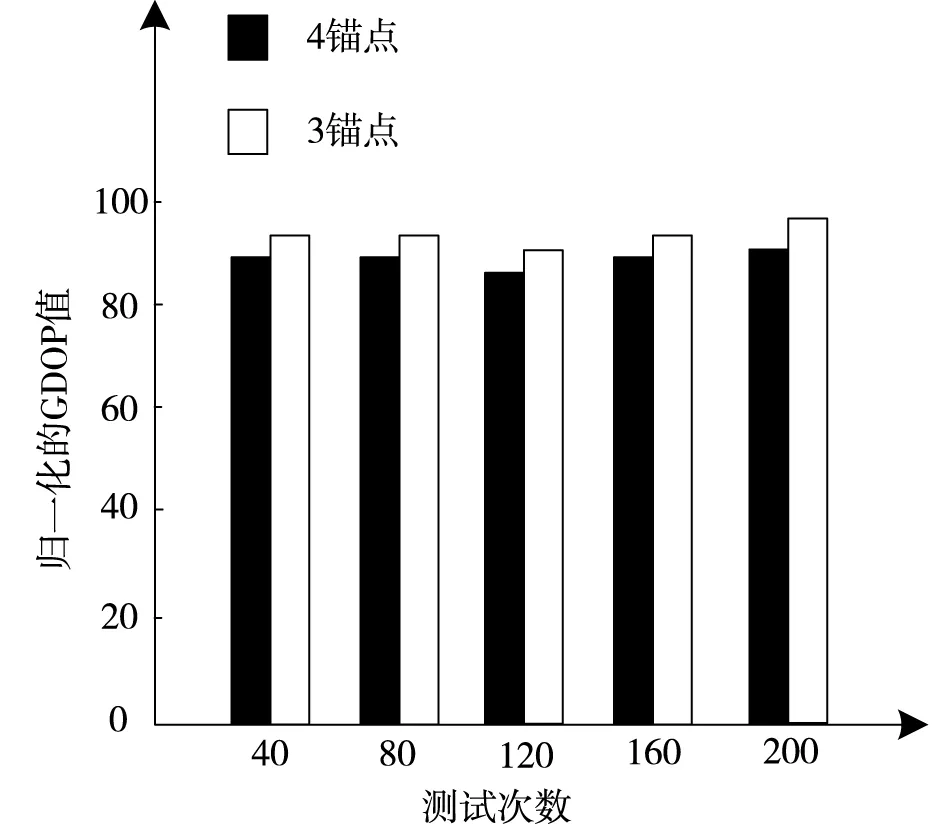
(b)外点图4 不同锚节点数量下，节点定位精度分析结果

由图4可知，采用本文方法分析后可知，当锚节点数量分别是3个、4个时，本文所提定位方法对无线传感器网络节点精度存在差异，目标节点定位后，内外点归一化GDOP值显示，3个锚节点的内、外点定位精度大于4个锚节点的内、外点定位精度。由此可知，锚节点数量需要合理设定，才能实现无线传感器网络高精度定位。

2.4 无线传感器网络节点移动速度对定位精度的影响

当锚节点数量是3个，几何分布如图2中A1、A2、A3为例，测试此条件下，当无线传感器网络节点移动速度是0.1mm/s、0.2mm/s、0.3mm/s、0.4mm/s、0.5mm/s时，本文所提定位方法对无线传感器网络节点的定位效果，定位效果用归一化GDOP值描述。测试结果如表1所示。

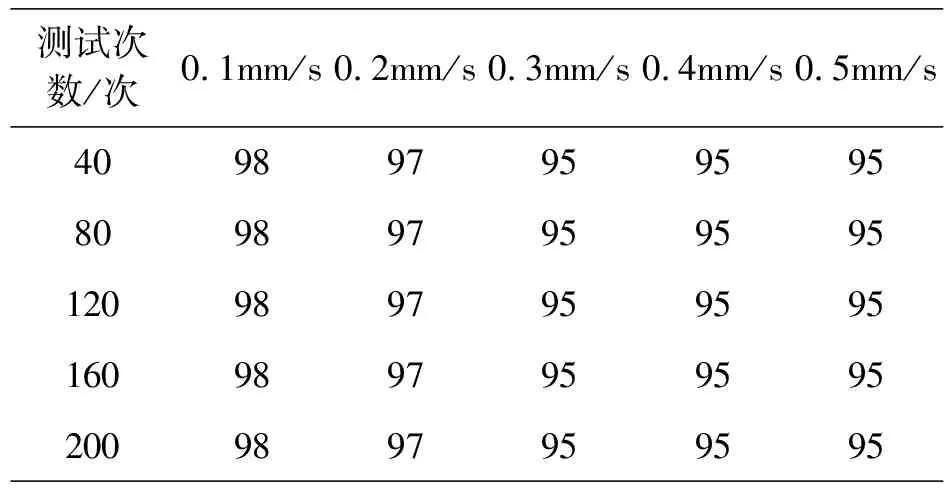
表1 无线传感器网络节点移动速度对定位精度的影响

由表1可知，采用本文方法分析后可知，当无线传感器网络节点移动速度是0.1mm/s、0.2mm/s、0.3mm/s、0.4mm/s、0.5mm/s时，本文所提定位方法对无线传感器网络节点定位后，归一化GDOP值出现变化。在无线传感器网络节点移动速度是0.1mm/s时，归一化GDOP值最高，此时定位精度最高。伴随移动速度的加快，本文所提定位方法对无线传感器网络节点定位精度变差，但定位结果的归一化GDOP值也不小于95。相对而言，无线传感器网络节点移动速度加快，对无线传感器网络节点定位精度存在微弱影响。

2.5 无线传感器网络节点移动距离对定位精度的影响

设锚节点数量是3个，几何分布如图2中A1、A2、A3为例，测试此条件下，当无线传感器网络节点在t时刻被定位后，t+1时刻移动距离是0.5m、1.5m、2.5m、3.5m、4.5m时，本文所提定位方法对无线传感器网络节点的定位效果，定位效果以归一化GDOP值描述，其中无线传感器网络节点移动速度是0.1mm/s。测试结果如表2所示。

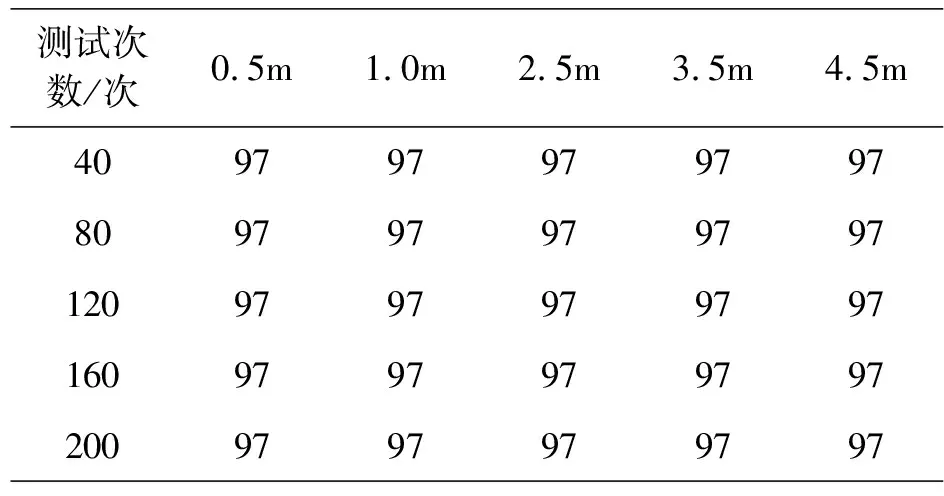
表2 无线传感器网络节点移动距离对定位精度的影响

由表2可知，采用本文方法分析后可知，当无线传感器网络节点移动速度是0.1mm/s、t+1时刻移动距离是0.5m、1.5m、2.5m、3.5m、4.5m时，本文所提定位方法对无线传感器网络节点定位后，归一化GDOP值是97，定位精度较高。伴随移动距离的增多，本文所提定位方法对无线传感器网络节点定位精度保持不变，定位结果的归一化GDOP值也始终是97。相对而言，无线传感器网络节点移动距离增多，对无线传感器网络节点定位精度不存在负面影响。

3 结论

综上所述，当锚节点几何布局和锚节点数量不同时，本文方法会对无线传感器网络节点定位的精度造成影响；当锚节点数量是3个且几何分布如图2中A1、A2、A3所示时，节点移动速度不同，本文方法会对无线传感器网络节点定位精度造成损失，但受损程度不大，且节点移动距离不同，文本方法不会对无线传感器网络节点定位精度造成影响。