从一题多解探析三重积分的计算方法

赵金虎

（阜阳师范大学 数学与统计学院，安徽 阜阳，230637）

1 引言

三重积分是高等数学中的一个重点，也是很多学生考研复习中的一个难点，因此，三重积分的计算成了近年来高等数学教学研究的热点问题。贾建文探讨了直角坐标系下三重积分的计算技巧，用不等式组的方法列出了三重积分化为累次积分的公式。[1]郑华盛介绍了三重积分交换积分次序的普适方法，并通过实例和应用验证了有效性。[2]蒋银山讨论了三重积分的几种计算方法，包括先一后二法、先二后一法、柱面坐标法、球面坐标法、积分区域的对称性与被积函数的奇偶性等。[3]吕中学通过实例检验了各种类型的空间体中三重积分的计算方法。[4]孟飞将二重积分在极坐标系下积分顺序的交换方法推广到了三重积分的球面坐标计算中。[5]井晨睿等对比研究了不同坐标系下三重积分的计算方法，根据被积函数以及积分区域的特点，提出了选取坐标系的方法[6]。曹秀梅、吴自库总结和推广了三重积分中“先二后一”的计算方法，通过例题拓展了计算技巧。[7]赵小艳和李继成通过例子详细说明了如何选取适当的方法计算三重积分，对于如何确定不同坐标系下的积分上下限进行了区分和总结。[8]刘菊青分析了三重积分在直角坐标系下的截面法，从理论上解决了三重积分计算的抽象性和合理性。[9]方汶铭指出变量置换是三重积分在柱（球）面坐标系中计算的本质，并讨论了不同坐标系中若干变形的处理方法。[10]

学生很难掌握三重积分的各种计算方法，主要原因在于积分区域是三维的，而学生的空间想象能力有限，导致三重积分转化为累次积分的时候，学生很难确定各个积分变量的积分限，这是困扰学生的一个主要障碍。鉴于上述背景，本文从可视化的角度，分析了同一道三重积分的四种计算方法，探讨了不同方法中分步骤选取各个积分变量上下限的有效策略，使学生能够全面地认识和掌握三重积分的各种计算方法。请看本文的题目其中V由曲面x2+y2=z2与z=1所围成[11]，如图1所示。

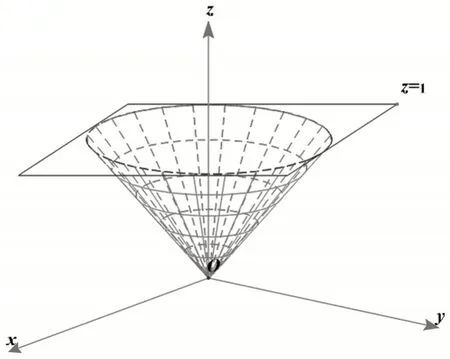
图1 积分区域示意

2 计算三重积分

2.1 截面法

截面法又称作“先二后一”法，首先把积分区域视为介于两个平行平面z=e和z=h之间的立体[12]，也就是考虑变量z能够取得的最大值与最小值，在本题中z∈[]0,1；然后用垂直于z轴的平面截积分区域，设所得截面为Dz（如图2所示），也就是把曲面方程中的z看作常数，在本题中此时将三重积分转化为先对变量x、y在平面区域Dz上的含参变量的二重积分，再对z∈[0,1]求定积分的形式。由于截面为圆域，平面区域Dz上的二重积分结合极坐标变换完成。用截面法解决本题的完整过程如下：

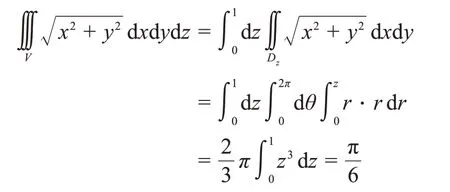
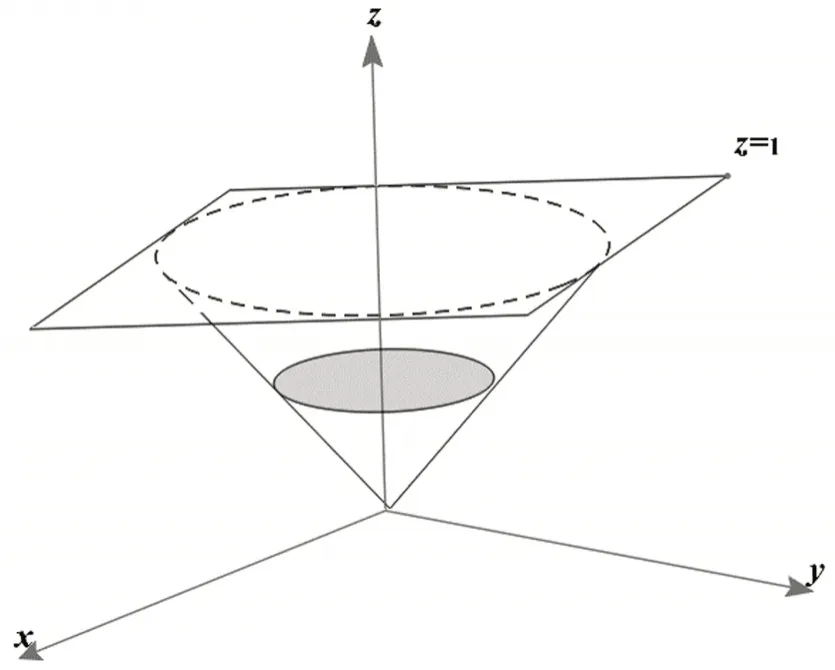
图2 .截面示意

2.2 投影法

投影法又被称作“先一后二”法，首先把积分区域视为柱体的一部分，投影区域D为类比的柱体底面，也就是将积分区域中垂直于z轴的最大平面区域作为柱体底面，在本题中圆锥面x2+y2=z2与平面z=1相交得到的圆为x2+y2=1，该圆域形成了投影区域D={(x,y)|x2+y2≤1}，如图3所示。然后确定变量z介于上下曲面z=z1(x,y)和z=z2(x,y)之间，在本题中z介于圆锥面与平面z=1之间。最后，三重积分转化为先对z的含参量积分，再形成对x、y的二重积分形式。同理，由于投影区域为圆域，关于x、y的二重积分可结合极坐标变换完成。用投影法解决本题的完整过程如下：

图3 投影示意

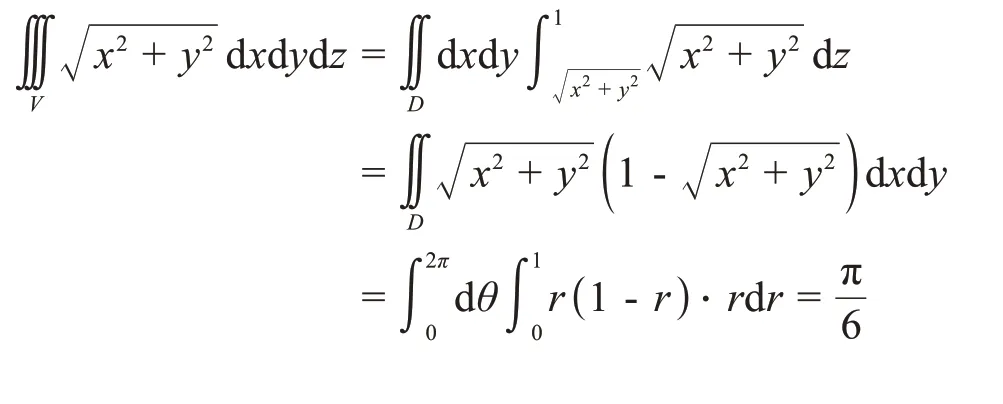
2.3 柱面坐标变换

柱坐标变换是计算三重积分的换元法中两个最常用的变换之一，当积分区域或被积函数含有x2+y2或x2+y2+z2时，可考虑使用柱面坐标变换。构成柱面坐标的三个坐标中，“r=常数”表示以z轴为中心轴的圆柱面，“φ=常数”表示以z轴为边缘的半平面，“z=常数”表示平行于坐标面xOy的平面。柱面坐标变换可以认为是投影加极坐标变换的过程，通常是先找出积分区域V在xOy平面上的投影区域D，然后确定变量z介于曲面z=z1(x,y)和z=z2(x,y)之间，并转化为r和φ来表示，在本题中投影区域D={(r,φ)|0≤r≤1,0≤φ≤2π}，z介 于z=与平面z=1之间，如图4所示。所以，利用柱面坐标变换解决本题的完整过程如下：

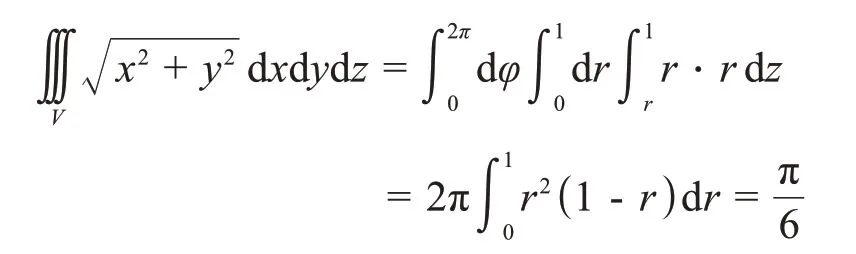
图4 柱面坐标示意

2.4 球面坐标变换

当积分区域或被积函数含有x2+y2+z2或x2+y2时，可考虑使用球面坐标变换。构成球面坐标的三个坐标中，“r=常数”表示以原点为中心的球面，“φ=常数”表示以原点为顶点，以z轴为对称轴的圆锥面，“θ=常数”表示以z轴为边缘的半平面。使用球面坐标变换时，需要把积分区域中直角坐标系下的方程都转化为球面坐标系下新的变量来表示，以此来确定球面坐标变量的积分限，没有限制条件的变量选取默认的范围，比如θ∈[ 0,2π]。在本题中，圆锥面x2+y2=z2转化为了cos 2φ=0，即此为与z轴夹角的上限；平面z=1转化为rcosφ=1，即此为球面半径的上限，表示积分区域限制在平面z=1以下，并不能超出这个平面到更外侧r=1的球面上（如图5所示）。利用球面坐标变换解决本题的完整过程如下：

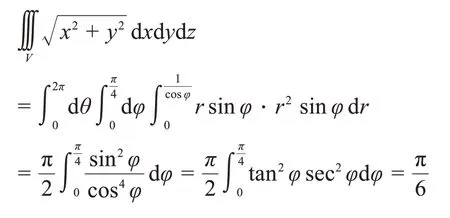
图5 球面坐标示意

3 结语

在学习三重积分的计算时，学生遇到的最大问题是难以获得各个积分变量的积分限。本文利用同一道三重积分的计算题，针对四种不同的计算方法，分析了如何快捷地把三重积分转化为累次积分。学生应当加强空间想象力的训练，加深对此类问题的理解，并做到触类旁通，举一反三，这样才能熟练掌握三重积分的各种计算方法。