基于多项式曲线拟合的六方轴直线度误差评定方法研究
2021-02-15殷浩林黄宇杭
周 娟,殷浩林,黄宇杭
(中国计量大学 质量与安全工程学院,浙江 杭州 310018)
六方轴因其具有良好的力学性能以及传动特性,常用作于深井泵的转轴[1]。六方轴的直线度直接影响着水泵的整体工作性能[2],直线度误差较大时会导致泵体剧烈振动,降低水泵的运作性能,甚至产生安全事故。随着科学技术水平的提高,水泵企业愈来愈注重满足高精度、高效率的需求。因此,如何提升六方轴直线度误差的评定精度与评定效率是亟待解决的问题。
目前,使用较为广泛的六方轴直线度误差测量方法为人工打表测量。这种方法比较依赖操作工的技术能力,需要花费大量培训成本,测量效率较低,且测量精度无法得到保证。因此,相关学者对六方轴直线度的测量方法进行了大量研究。文献[3]和文献[4]采用计算机视觉技术、图像识别与处理技术测量直线度误差,该方法对于零件和CCD相机之间的相对位置精度要求较高,测量系统的装配成本较高。文献[5]利用激光位移传感器并结合光学三角法进行位移测量,该方法测量精度较高,但所使用的激光传感器需要通过导轨进行位置变换,容易产生较大误差,若采用高精度导轨则会增加成本。文献[6]提出了一种基于全站仪自由设站法的直线度测量方法,该方法采用两端点连线法评定直线度误差,鲁棒性较差。文献[7]对轴截面法进行了改进,提升了轴截面法测量轴直线度的精度,但只能对一个轴界面进行测量,无法反映整根轴的直线度误差情况。文献[8]采用滑台结构使测量元件进行轴向移动,从而测量轴类零件直线度,该方法只能测量某一轴向截面上的直线度误差,且滑台精度要求较高。文献[9]提出了一种基于最小二乘圆的圆柱体零件直线度误差评定方法,并将轴的中心线偏移情况可视化。
本文基于多项式曲线拟合方法,提出了一种六方轴直线度误差评定方法。通过位移传感器测量六方轴各外表面的挠度偏移情况,将采集数据传输至计算机并进行运算处理,经由多项式拟合获得整根六方轴的中心线偏移情况,最后将曲线合成并计算得出六方轴直线度误差。该方法提升了六方轴直线度误差评定的效率,且保证了一定的精度。
1 测量方法与原理简介
基于对六方轴直线度误差测量的需求,本文提供了一种六方轴直线度测量机。本文所设计的六方轴直线度测量系统结构,通过左右两端所设置的回转测量模块夹持待测六方轴,双侧装夹可以减小轴心偏移矢量坐标的定位误差;位移传感器等距分布在待测六方轴下方采集数据,传感器通过固定装置定位,从而提高采集数据的精确性。系统总体结构主要包括:气动三爪卡盘、两通旋转接头、位移传感器及其支撑装置、同步带、感应开关、气缸、伺服电机。
在实际测量时,两通旋转接头接有通气管,气阀通气动作可以控制气爪元件抓取待测六方轴,并通过气缸推进其至检测工位;通过软件控制旋转驱动电机带动气爪元件夹持六方轴进行旋转,卡盘中的三个槽对应六方轴等相邻角度的三个外表面;每当卡槽经过感应开关时会产生感应信号,控制器在接受感应信号后发送检测指令使位移传感器进行数据采集。
由于位移传感器所采集的数据仅是六方轴每一外表面上的相对位移量,无法直接获取直线度误差,因此需要通过坐标转换的方式将位移传感器所采集的数据转换为六方轴截面中心点的三维坐标,以此来计算六方轴直线度误差。(需要通过相对面数据相减求解每组相对面方向上的挠度偏移量,经坐标转换为采样点所在截面实际中心点的二维坐标,以便后续进行多项式曲线拟合)
将六边形的六个外表面按顺序编号为1至6依次标记,则标号为1的外表面与标号为4的外表面相对。同理,外表面2与5相对,外表面3与6相对。假设三组相对面方向定义为方向A,方向B,方向C。
以外表面1与4所对应的方向A为例,侧头测量动作示意图如图1。

图1 测头测量动作示意图Figure 1 Schematic diagram of probe measuring action
位移传感器所读取数据分别为δ1和δ4,以第1面的挠度数据δ1作为基准,第4面的挠度数据δ4相对于δ1所产生的变化即为方向A上的偏移量,该偏移量Δ可表示为
(1)
可建立A、B、C三方向及x、y方向的复合坐标系如图2。

图2 截面中心点偏移复合坐标系示意图Figure 2 Composite coordinate system diagram of center point migration of section
轴心O′的位置可使用两种不同的方式进行描述,分别为O′(δA,δB,δC)及O′(δx,δy)。若记点O′到坐标原点O的距离为δO′,则两组不同的坐标之间的关系可用如下公式来表达:
δA=sinθ·δO′=δy,
(2)
(3)
(4)
将上式转换为矩阵形式为
(5)
记:
(6)
矩阵H的广义逆矩阵如下:
(7)
则(δx,δy)可表示为
(8)
(9)
通过上式计算可获得所有测量点相对于理想六方轴中心线的偏移位置坐标,并以此建立xyz三维坐标系如图三。

图3 六方轴xyz三维坐标系Figure 3 Hexagonal axis xyz three-dimensional coordinate system
将点分别投影到xz平面与yz平面上,再通过曲线拟合技术取得六方轴在xz方向和yz方向的总体偏移情况,根据后续相应公式即可计算六方轴的直线度误差。
2 多项式曲线拟合测量算法
多项式曲线拟合方法广泛应用于轴类零件的直线度误差测量,当测量点较少时也可求解整根轴的中心线偏移情况。
2.1 总体算法思路
计算机在读取位移传感器所测得的数据后,首先需要对数据进行预处理。预处理的主要目的是将所测量的原始数据转化为x和y方向上的偏移量,这两个偏移量即可与测量点位置z组合成为xyz三维坐标系。
接下来将三维问题转化为二维问题进行求解。对xz和yz两个平面上的点进行多项式拟合,分别得到x=h(z)和y=g(z),则可获取六方轴在这两个投影面上的中心线偏移情况。若两个多项式函数都没有发生过拟合情况,可通过其计算六方轴直线度误差;若在过拟合检测与残差检测中出现异常情况,如测量直线度误差数值过大或残差分布异常等现象,则重新进行测量。
总体算法流程图如下图所示:

图4 整体算法流程图Figure 4 Flow chart of overall algorithm
2.2 多项式拟合原理
完成采样点的数据采集后,需要对其进行多项式曲线拟合,最终计算出直线度误差。
根据泰勒定理,假设六方轴中心曲线是一个无穷多项式:
y=f(x)=a0+a1x+a2x2+…+anxn。
(10)
其中,a0,a1,…,an为每一项的系数。
式(10)中,x为传感器所处的位置,9个传感器同时进行测量,一共可获得11组数据(加上夹持端);而y是随着采样点位置变化而变化的中心线偏移量。将一组采集数据定义为(xi,yi)(i=1,2,…,11),求解y=f(x)的一个近似表达式y=g(x),计算公式如下:
(11)
根据最小二乘法原理,令(xi,yi)(i=1,2,…,11)对拟合函数y=g(x)的偏差平方和δ达到最小,计算公式如下:
(12)
将11组数据代入式(11)中,则可得:
(13)
记:
(14)
(15)
(16)
根据式(14)、(15)、(16),将式(13)转换为:Cα=γ。建立正规方程:
CTCα=CTγ。
(17)
该正规方程为aj(j=1,2,3,…,n)的线性方程组。若系数行列式|CTC|不为0,则可求得方程组(13)的位移最优近似解,使得y=g(x)的偏差平方和δ取得最小并求解该拟合函数。
由六方轴直线度检测原理可知,x1,x2,…,x9互不相同,式(16)矩阵C的秩为n+1,则CTC非奇异,说明方程组(13)的解存在且唯一。
2.3 直线度误差评定方法
常用的平面直线度评定方法有两端连线法、最小二乘法和最小包容区域法[10],这三种方法都依据采样点到基准轴线的上下偏离值之和|hmax-hmin|来表示直线度误差[11]。如图5。
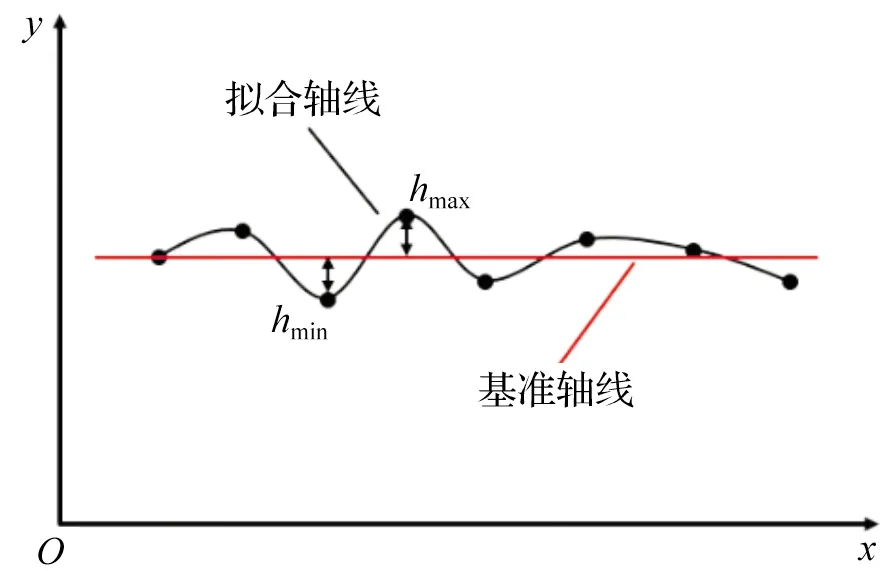
图5 直线度判定示意图Figure 5 Schematic diagram of straightness evaluation
根据上述两个多项式函数确定六方轴中心线与基准轴线的最大、最小偏差值,计算公式如下:
(18)
其中,S(z)本质上是一个符合函数,可表示为S(h,g)。对于第一个采样点而言,其增量可表示为
ΔS=S(z1)-S(z0)。
(19)
根据微分定理,式(19)可表示为
ΔS≈dS=S(z0)′(z1-z0)。
(20)
则有
(21)
根据式(21)可得到所有采样点处函数值的推广函数:
(22)
其中,z为连续变化的数,则k可取无穷大,而在计算机处理此函数时,无法对无限多个z进行分析,因此需要借助微元差分的思想对上式进行处理。通过设置k的数量来控制z的数量。轴的长度为500 mm,若设置k为500,则说明是以1 mm为步长进行分析,以此类推。本文设置k为5 000,使计算机在保证效率的情况下尽可能分析更多的点。将第一个分析点表示为
(23)
则S(0)的下一项可表示为
(24)
选取其中最大的数值S(z)max为六方轴中心线相对于基准轴线的最大偏移量,最终六方轴的直线度误差可表示为
Φ=2maxS(z)。
(25)
2.4 多项式拟合过拟合情况分析
多项式曲线拟合是基于最小二乘原理求解拟合函数值与样本点之间的偏差平方和,若拟合次数不够高,则会出现大多数样本点不在拟合曲线上的情况,拟合精度无法得到保证;若拟合次数过高则会出现过拟合的现象,如图6。
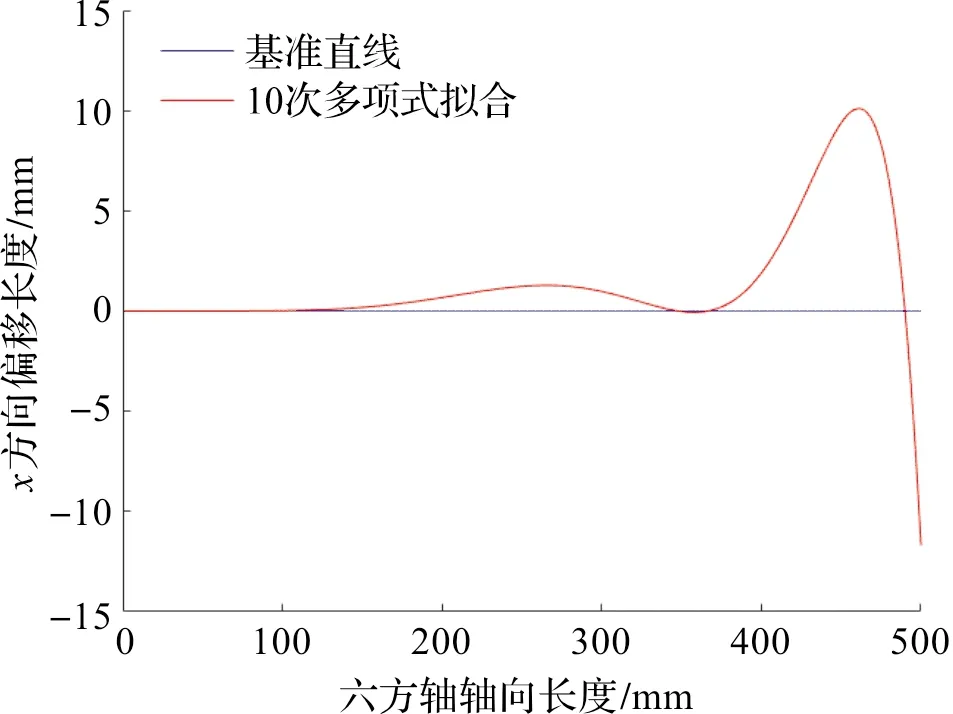
图6 多项式拟合出现的过拟合情况Figure 6 Overfitting of the polynomial fitting
当出现过拟合时,虽然拟合曲线尽可能经过所有样本点,但与基准轴线之间会出现偏差过大的情况,有时会达到精确值的10倍以上。此时,输出的直线度误差不具备任何参考价值。
当拟合次数较低时,拟合曲线往往不能准确反映整体六方轴直线度,因此在部分情况下会出现曲线上的点比样本点更加接近基准轴线,导致最终输出的直线度误差是一个较小的值。
在实际拟合过程中,随着拟合次数的增加,拟合曲线更加光滑,通过比较得出拟合次数为4~6次时为最佳。图7为拟合次数分别为4、5、6时的拟合曲线。
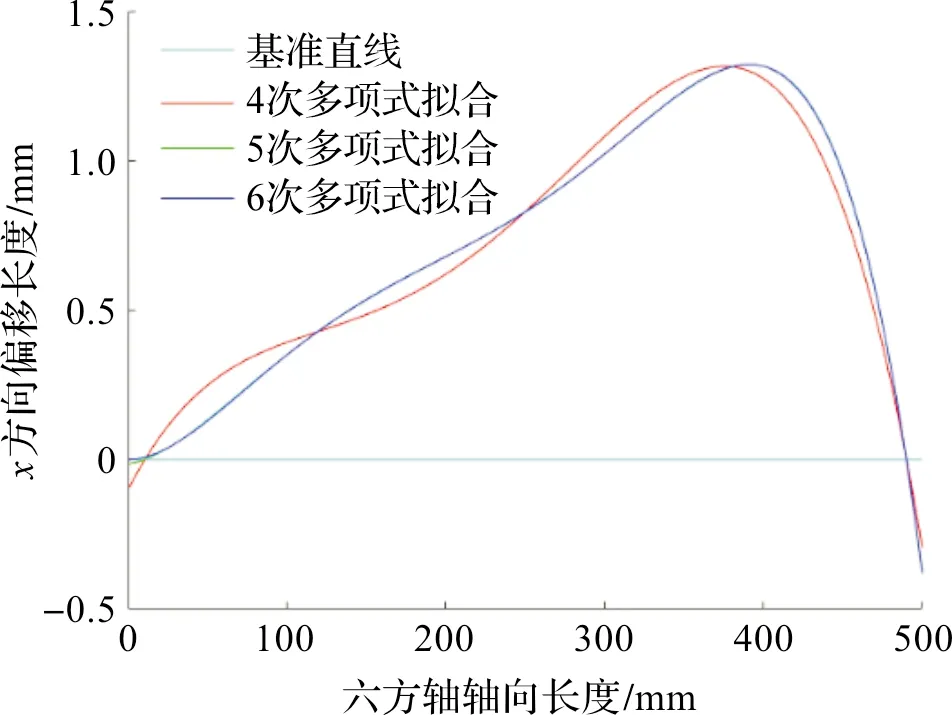
图7 拟合次数4、5、6次曲线放大比较Figure 7 Amplitude comparison of 4th、5th、6th degree polynomial fitting
如图7所示,4次拟合曲线与5、6次拟合曲线有显著偏差,5次拟合曲线与6次拟合曲线基本重合。因此,在多项式拟合中,5次拟合与6次拟合的效果基本相同的。为了尽可能减少发生过拟合的情况,使用5次多项式获取拟合曲线。若最终获得的直线度误差数值明显过大,则说明存在隐性过拟合的现象,需要查看具体拟合曲线;若具体拟合曲线震荡幅度过大,则需要减少拟合次数,重新进行拟合。
2.5 拟合准确性分析
在排除过拟合这种极端情况后,需要对拟合曲线进行分析,采用拟合优度来表示拟合结果的准确性。
拟合优度的计算公式如下:
(26)
其中,ESS为回归平方和,TSS为总体平方和,二者计算公式如下:
(27)
(28)
若拟合优度R越接近于1,说明拟合的准确性越高;反之则越低。一般拟合优度R高于0.9时,则认为此次拟合的准确性较高,且拟合结果可信度较高。
此外,还可以用残差图分析法对拟合情况进行分析。残差是因变量的观测值与回归方程求出的预测值之差,其表示为
(29)
在作残差图前需要将残差进行标准化计算,以便判断异常点位置,计算公式如下:
(30)
其中,sei为第i个残差的标准差,其计算公式如下:
(31)
使用标准化残差绘制ei-xi残差图可轻松辨别2σ内的数据(数据落在2σ范围内的概率为95%),落在2σ外的数据则会被判定为异常数据,需要对该点进行重新测量,再使用重新测量的数据进行二次拟合,获得更加准确的直线度误差数值。
3 结果及讨论
实验仪器为六方轴直线度测量机,如图8。

图8 六方轴直线度测量机Figure 8 Hexagonal axis straightness measuring machine
本次测量使用9个传感器,并外加2个靠近装夹端的传感器,以便消除装夹端处气爪的回转误差。使用这11组采样点的偏移数据进行多项式曲线拟合,并计算直线度误差。
传感器采集的各测量点位移数据如表1。
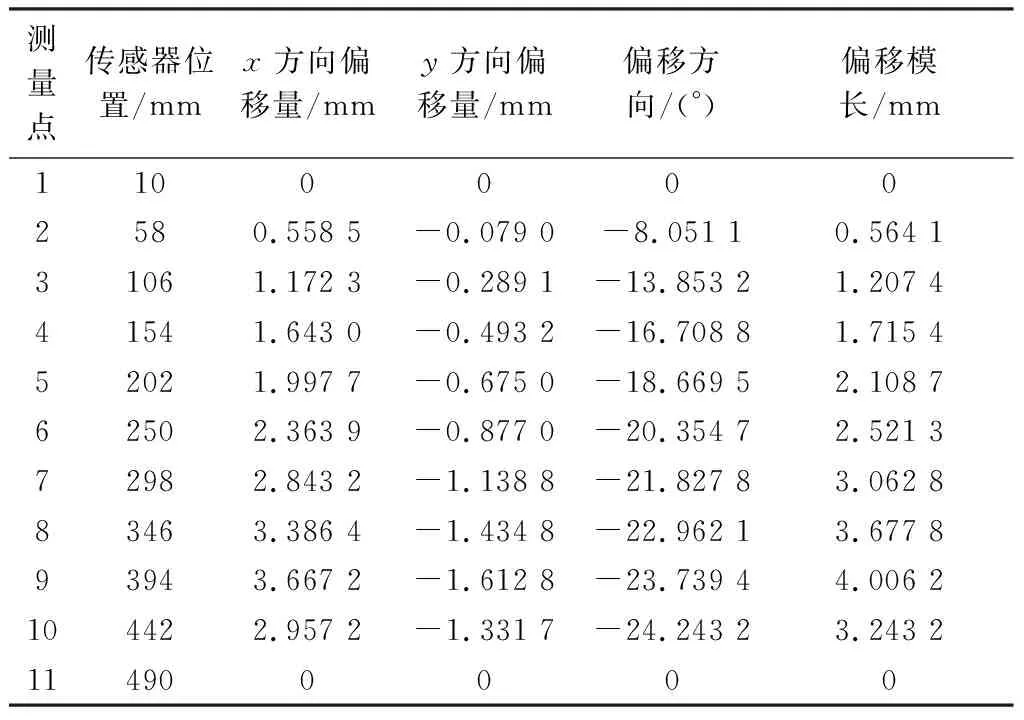
表1 六方轴直线度测量结果Table 1 Results of hexagonal axis straightness measurement
在六方轴直线度测量系统中可获得各测量点处轴心分布、轴心极坐标以及整体轴曲线情况如图9、图10。

图9 各采样点轴心坐标分布情况Figure 9 Result of Measurement system coordinate position interface
图10 六方轴中心线拟合结果Figure 10 Result of three directions axial displacement of the hexagonal axis
为验证直线度误差测量结果的准确性,本文使用更高精度的三坐标测量仪(CMM)对同一根六方轴的直线度进行测量,所使用CMM型号为Innova Classic。相关文献指出[13],在测量轴类零件直线度时,扫描密度为2 p/mm(每毫米两个测量点)时即可获得较为精准的测量值,因此本文在使用CMM进行测量时也采用这一测量方案。采用CMM进行重复10次测量消除随机误差,最终获得该六方轴的直线度误差数值为3.938 1 mm。
根据表1的测量结果,分别对xoz平面和yoz平面进行多项式拟合操作,得到拟曲线如图11、12。
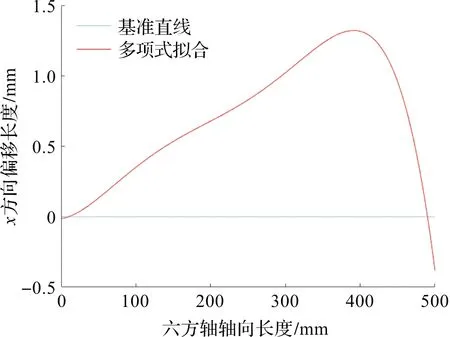
图11 xoz平面多项式拟合结果Figure 11 Result of polynomial fitting in the xoz direction

图12 yoz平面多项式拟合结果Figure 12 Result of polynomial fitting in the yoz direction
两个方向上的偏移数据如表2。
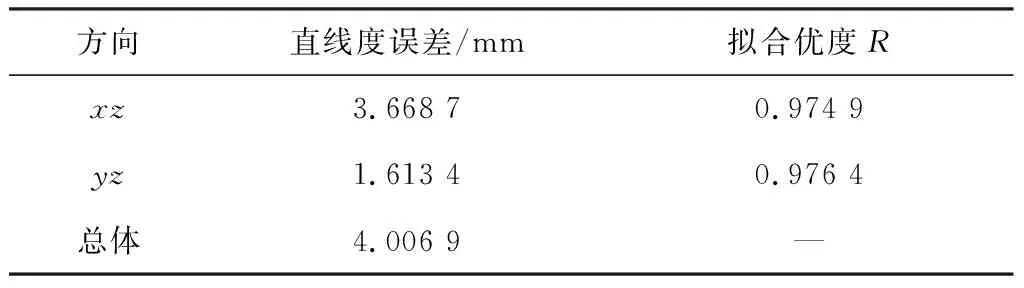
表2 xz方向与yz方向直线度误差数值Table 2 Straightness error value of xz direction and yz direction
根据上述测量结果可判定该六方轴的直线度误差为4.006 9 mm,即Φ=2maxS(z)=4.006 9 mm。
绘制残差图如图13、图14。

图13 xoz平面拟合残差图Figure 13 Residual diagram of xz-direction
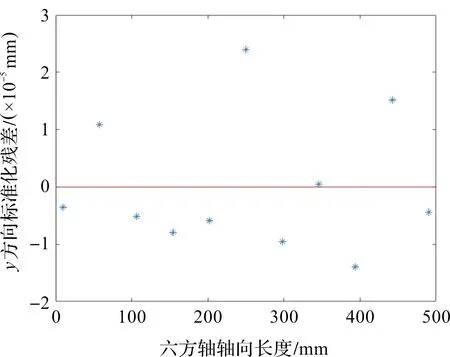
图14 yoz平面拟合残差图Figure 14 Residual diagram of yz-direction
由上述残差图可知,所有残差点都落在了2σ范围内,结合表2中的拟合优度,表明此次拟合结果有较高的准确性和可信度。
在轴类零件直线度的曲线拟合中,除多项式拟合外,较为常用的便是样条插值拟合[14]。所谓样条插值,即给定某些特定点,构造样条曲线或对其进行曲面插值。在样条插值方面,分段低次样条插值计算简便、稳定性高、收敛性较好,且易于计算机实现,但只能保证各段曲线在连接处的连续性,不能保证整条曲线的光滑性[15];而三次样条插值提高了函数曲线的光滑性,更加符合轴类零件的实际形状。因此,本文选择使用三次样条插值进行拟合对比。多项式拟合与样条插值拟合曲线对比如图15。
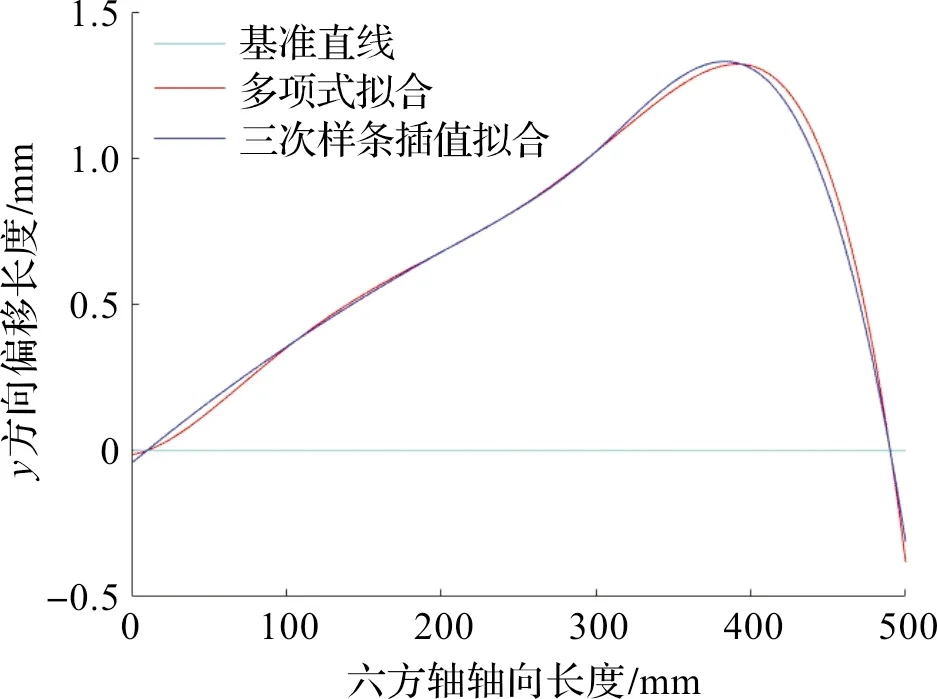
图15 两种拟合曲线对比Figure 15 Comparison of two kinds of fitting curves
二者实验结果对比如表3。

表3 两种曲线拟合方式结果对比Table 3 Comparison of the results of two curve fitting methods
如图14和表3所示,多项式拟合所得该六方轴直线度误差为4.006 9 mm,三次样条插值拟合所得直线度误差为4.032 1 mm。
多项式拟合与三次样条插值拟合是两种截然不同的拟合方式,二者得出的直线度误差之间存在一定的差别,因此在一定的工况下选择不同的拟合方式将影响最终直线度误差的准确度。
多项式拟合所得出的结果更接近CMM的测量结果。由于三次样条插值拟合必然会经过测量点,且两点之间所插入的曲线为三次曲线,所以拟合出来的曲线距离基准轴线的最大值会大于最大偏离点的偏离距离,则最终获得的直线度测量结果是偏大的。
使用六方轴直线度测量机及三坐标测量仪对十根不同的六方轴进行了直线度误差的测量,实验结果如表4。
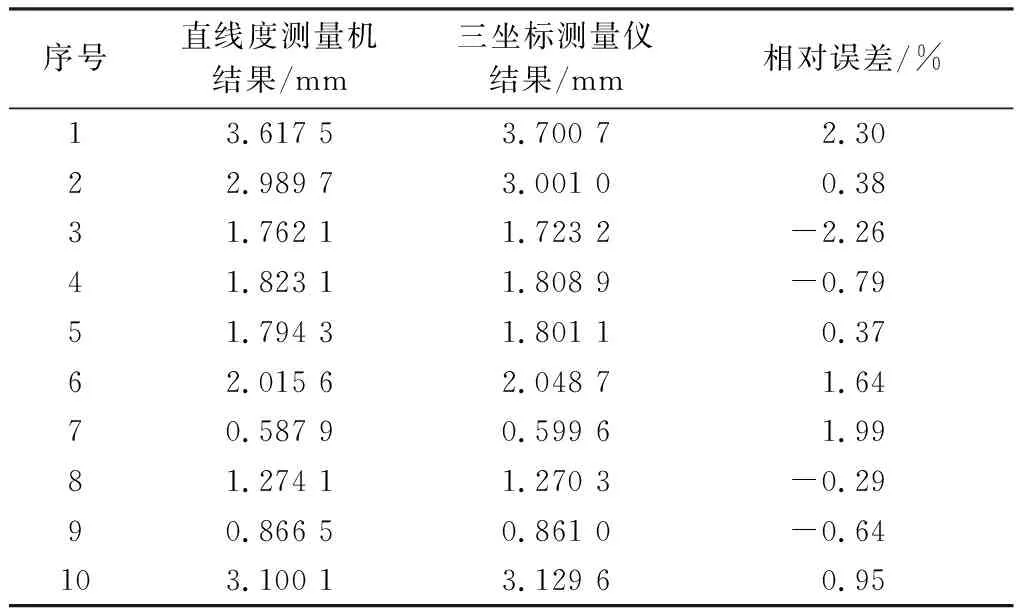
表4 十根六方轴直线度测量结果Table 4 Measurement results of ten hexagonal axis straightness
上述实验结果表明:多项式拟合所得直线度误差与CMM测量结果的相对误差小于5%,说明该方法能较为准确地评定六方轴直线度误差。
4 结 语
本文提供了一种基于多项式拟合的六方轴直线度误差评定方法,并对该方法进行了实验验证,得出了以下结论:
1) 该方法通过位移传感器测量六方轴个外表面的挠度位移数据,并将数据传输至计算机,计算机通过数据预处理、多项式曲线拟合、拟合曲线合成最终输出六方轴直线度误差测量结果;
2) 本文对多项式拟合的过拟合情况及准确度判定进行了讨论,当拟合次数为5次时拟合曲线效果较好,且发生过拟合情况的概率较低,并结合拟合优度和残差图分析方法对拟合曲线准确度进行了分析;
3) 本文对评定方法进行了实验验证,将实验结果与CMM测量结果进行了对比,证明了该方法具有较高的测量精度。
