高速飞行器追逃博弈决策技术
2021-02-14崔雅萌王会霞郑春胜胡瑞光
崔雅萌 王会霞 郑春胜 胡瑞光
1.北京航天自动控制研究所北京100854 2. 宇航智能控制技术国家级重点实验室北京100854
人工智能技术是引领新一轮科技革命和产业变革的战略性技术, 智能技术已成为大国博弈的重点[1]. 未来战争也将是智能化、体系化对抗, 传统的规则化、简单逻辑的博弈策略不能满足要求,发展智能装备,采用智能飞行器集群作战将成为创新性、颠覆性的作战模式[2]. 面对复杂的多飞行器拦截场景,单个飞行器逃逸成功很难实现,而诱饵伴飞、主动机动突防等策略可以帮助飞行器逃逸成功[3−5]. 在飞行器攻防对抗中,进攻方飞行器是逃逸者,需要找到最优策略成功逃逸;拦截方飞行器是追捕者,需要准确识别目标成功拦截,双方构成追逃博弈问题.
从进攻方(也称为逃逸方)角度研究逃逸策略,现有的多对一拦截场景大多基于传统的控制理论,在双方信息全部已知的情况下设计固定的策略求解问题,见文献[3−4,6−8].
从拦截方角度研究拦截策略, 多目标拦截问题需要考虑对抗双方性能, 结合对抗场景中双方的位置、速度、姿态等信息, 确定最优分配方案, 实现资源利用最大化并获得最佳打击效果, 是一种组合优化问题.目标分配方案有改进差分进化算法[9]、匈牙利算法[10]、蚁群算法[11]、粒子群算法[12−13]等. 众多方法中, 匈牙利算法计算量小, 求解方便快速, 易于实现,适合需要进行实时目标分配计算的对抗场景.
近年来人工智能技术迅速发展并日益成熟, 无论是逃逸方还是拦截方的策略研究都在从传统的求解方法转向智能博弈对抗方法[14−15]. 智能博弈对抗可以根据自身状态和感知的对手状态进行决策, 通过与环境不断交互进行学习来与对手博弈, 并不需要知道对手策略, 面对复杂多变的对抗场景具有一定优势. 目前智能博弈的方法在无人机集群等低速飞行器的决策对抗领域取得一定进展, 但在高速飞行器攻防对抗中应用较少, 面对此类问题时也仅使用固定方案[15], 且只考虑了单一策略, 如只进行抛撒诱饵策略或机动策略的研究[3,15]. 复杂作战场景下单一的突防策略难以保证飞行器突防成功,因此,需要多种策略相结合并适应战场态势变化. 本文解决了高速飞行器面对动态变化的多飞行器拦截时难以逃逸成功的问题,使其可采取抛撒诱饵、机动变弹道和姿态调整多种策略进行博弈.
本文将高速飞行器的攻防对抗问题抽象成多智能体博弈问题; 针对逃逸方飞行器建立含有抛撒诱饵、机动调整、姿态调整行为的多策略行为模型,加入先验知识提升算法收敛速度; 建立飞行器威胁矩阵, 针对拦截方飞行器设计变目标的动态目标分配算法;在三维环境下进行仿真验证. 考虑到对战场态势的动态适应性,奖励函数设计考虑抛诱饵的时机、抛诱饵的数量、机动时间. 仿真结果表明该算法通过训练得到的神经网络能够实时解算出飞行器的突防策略,控制飞行器实施逃逸.
1 红蓝飞行器相关数学模型
文中称逃逸方为红方,拦截方为蓝方.对抗中,红蓝双方可获得用于决策的信息是不对称、不完整的,双方所获得的信息及诱饵误判概率均由可获得完整信息的白方给出.
为简化问题,假设红蓝双方在真空中飞行;处于均匀引力场中; 红蓝双方为刚体、质量不变化; 只考虑红蓝双方飞行器在三维空间中的质心运动, 其姿态变化受姿态指令控制.
采用欧美体制的“北东下”坐标系,定义符合右手定则的空间直角坐标系.
1)惯性坐标系SG(OGXGYGZG)
惯性系坐标原点OG取在惯性空间某一点. 轴OGXG和轴OGYG在水平面内,轴OGXG指向正北,轴OGYG指向正东,轴OGZG满足右手定则铅垂向下.
2)机体坐标系ST(OT XTYTZT)
机体坐标系固连于飞行器, 坐标原点在飞行器质心OT. 轴OT XT位于飞行器对称平面内, 平行于机身轴线指向前方.轴OTYT垂直于飞行器对称平面(即xTOTZT平面),指向右方.轴OTZT位于飞行器对称平面内,垂直于xT轴朝下指向飞行器腹部.
1.1 红蓝双方行为模型
1.1.1 红方质心运动模型
惯性系下,红方位置、速度的动力学方程:

式中,pr为红方的位置矢量,vr为红方的速度矢量,Fr为红方的推力矢量,gz为重力加速度其只在轴OGZG方向有.
惯性系下红方推力矢量由机体系通过坐标系转换得到Fr=Trt→g·Fesc,其中,Trt→g为红方机体系到惯性系坐标转换矩阵,各元素由红方姿态角计算.
1.1.2 红方机动调整模型
红方飞行器的机动装置可以在红方机体系OTYT轴和OTZT轴的正向和负向产生固定大小的推力. 由于燃料限制, 机动装置累计工作有限.忽略机动装置开机、关机过程中推力的过渡过程. 关机时推力为0,开机时推力大小为Fesc. 记Kesc,y,Kesc,z为红方机动指令,Kesc,y,Kesc,z∈{−1,0,1}. 机动装置产生的作用力在机体系下的各轴投影分量如下式:

1.1.3 红方姿态调整模型
红方飞行器的姿态调整装置可以在一定程度上改变其姿态角. 姿态角调节范围不受限制,但其角速度有约束. 在k(k=0,1,2,···)时刻:

在k(k= 0,1,2,···)时刻,根据当前时刻的姿态角指令、上一时刻的姿态角,按下式计算姿态角:
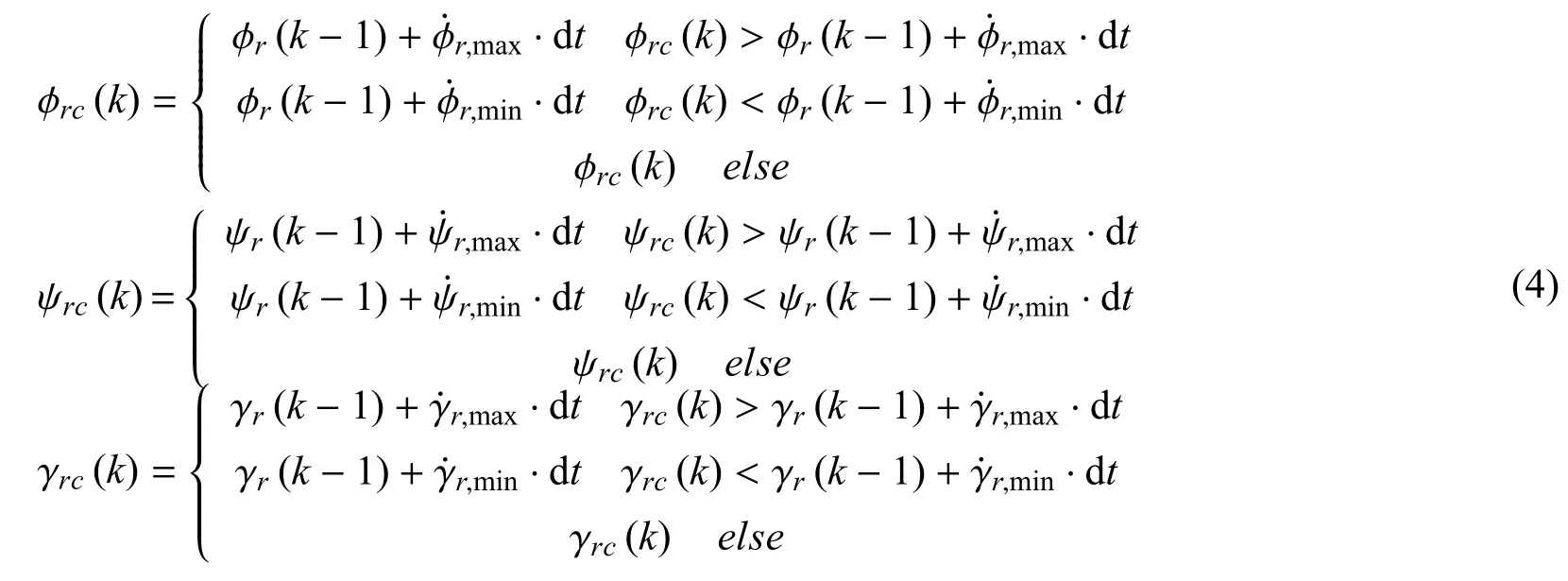
按式(5)计算姿态角速度:

式中, dt为仿真周期,φrcψrcγrc分别为俯仰、偏航、横滚姿态角指令.
1.1.4 蓝方行为模型
蓝方给定策略为采用比例导引法拦截红方, 其制导指令为:

式中,ky、kz为比例导引系数,表示红方与蓝方的视距的变化率,分别表示视线高低角的变化率和方位角的变化率.
1.2 红蓝双方相对运动关系
红方与蓝方的相对运动关系用以下方程描述:

式中,X、Y、Z为红蓝双方相对位置,Vx、Vy、Vz为红蓝双方相对速度, η 为视线离轴角,TTTg→t为惯性系到机体系的坐标转换矩阵, 各元素由姿态角计算.分别为红蓝相对距离变化率、视线高低角速率.
1.3 诱饵作用模型
红方飞行器载有一定数量的诱饵, 可根据博弈对策逐个释放或同时释放若干个. 释放后的诱饵以一概率pcheat使蓝方识别为红方本体.
记Kbait,i为红方释放第i个诱饵的指令,Kbait,i=0 为不抛出第i个诱饵,Kbait,i=1 为抛出第i个诱饵,若第i个诱饵状态为Kbait,i=1,则此诱饵无法再次抛出.记第i个诱饵在tbait,i时被释放,抛撒诱饵的方向由飞行器抛撒时的姿态角决定. 释放后诱饵只在重力作用下保持匀加速度运动.
在惯性系,第i个诱饵在释放时的位置即为红方此时质心位置,在释放时的速度为:

式中,mesc,bait为红方携带诱饵数量,vbait为惯性系下红方抛诱饵时刻的速度,vxr(tbait,i),vyr(tbait,i),vzr(tbait,i)为惯性系下红方抛诱饵时刻的速度分量.
当红方释放一枚诱饵时, 该诱饵被误判概率为pcheat,由释放诱饵时的红蓝相对距离确定,如下式:
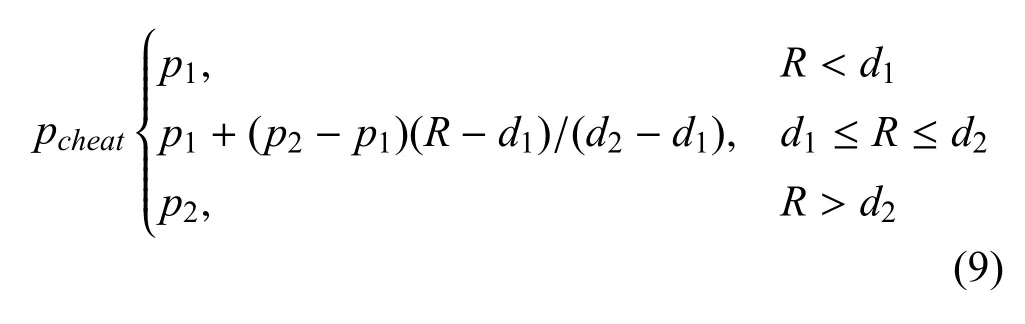
白方计算误判概率同时生成一个随机数n,取值范围(0.05 ~0.95).n若小于pcheat,则蓝方将诱饵误判为红方本体;否则,蓝方识别其为诱饵.
2 蓝方飞行器目标分配策略
多飞行器对多个目标进行打击时, 需要在较短的时间内对跟踪空域中的目标进行合理分配, 实现对目标群的杀伤概率最大, 并避免重复攻击与遗漏[9]. 结合红蓝双方对抗特点及红方所携带诱饵特性, 优化目标分配模型[16−17], 采用匈牙利算法, 根据红方实体数量变化进行动态目标分配策略调整.
2.1 目标分配的数学模型
蓝方对红方的特征分布未知, 只能根据不完备信息采取相应策略, 故本文选择非参量法进行目标分配的数学建模,根据红蓝飞行器间角度、距离、速度以及蓝方对红方各实体的识别概率、辐射源等参数构造红蓝综合威胁函数.
2.1.1 识别概率
假设蓝方能准确识别到红方, 但红方抛出的诱饵具有一定欺骗性,不能被准确识别.识别诱饵的概率与红蓝双方距离有关, 此概率服从诱饵欺骗概率,因此,构造识别概率如下:

2.1.2 角度威胁
当蓝方朝着红方飞行时, 蓝方更容易探测到目标进而执行拦截任务,因此,构造角度威胁函数如下:

式中,a=0.000 1R,R为红蓝相对距离.
2.1.3 距离威胁
当红蓝相对距离r≫Rmax或r≪Rmin时,认为距离优势相对小; 当R0= (Rmin+Rmax)/10 时, 认为距离优势最大构造,因此,构造距离威胁函数如下:

式中,R0=(Rmin+Rmax)/10,Rmin和Rmax分别为红方飞行器最近和最远探测距离.
2.1.4 速度威胁
当蓝方速度比红方速度大时, 蓝方更易拦截到红方,因此,构造红蓝之间的速度威胁函数如下:
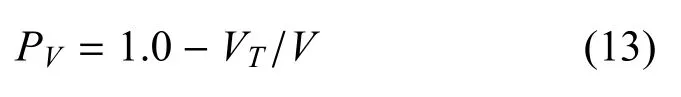
式中,VT和V分别为红方和蓝方速度.
2.1.5 蓝方与红方辐射源之间的威胁
蓝方拦截目标时, 根据质心干扰原理跟踪红方及其诱饵的红外辐射能量中心. 由于红外诱饵产生强于红方数倍的辐射源, 随着诱饵飞行不断远离红方,其将诱导蓝方偏离目标红方[17],故建立如下红蓝辐射特性匹配威胁函数:

式中,设定nc>nd,即诱饵与蓝方之间的辐射源威胁更高.
2.1.6 综合威胁函数
根据式(10)~式(14),可构造红蓝之间的综合威胁函数,其表达式如下:
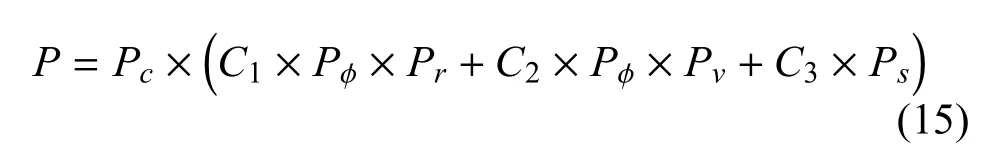
式中:C1、C2、C3分别为权系数, 0 ≤Ci≤1 且C1+C2+C3=1,其值由各威胁对综合威胁的影响的大小决定.
2.1.7 威胁矩阵
设对抗场景中有蓝方m个飞行器, 红方n个飞行器(含诱饵),可以得到的红方第i枚蓝方飞行器对红方第j个目标的动态威胁函数值Si j,从而可以建立起如下红蓝威胁矩阵:
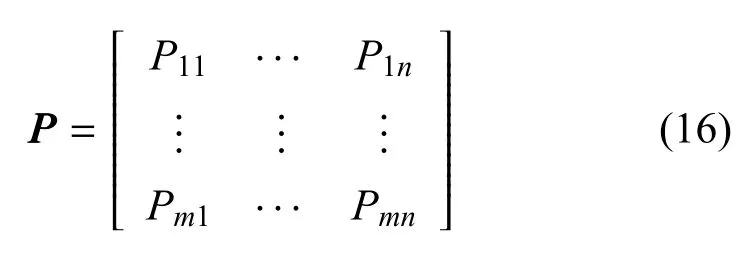
则目标分配问题可描述如下:

式中,Xi j为决策变量,取值1 表示第i枚蓝方飞行器被分配给第j个红方,Tj为蓝方第j个飞行器,约束条件1 表示蓝方一个飞行器只能攻击红方一个飞行器, 约束条件2 表示红方飞行器j最多只能被蓝方Tj个飞行器攻击.
2.2 动态目标分配算法
蓝方多枚飞行器均受决策层指挥, 决策层接收各蓝方飞行器感知的信息后, 根据红方飞行器数量采取相应目标分配策略, 将分配结果反馈给蓝方各飞行器, 蓝方各飞行器接收到分配指令后对指定目标进行拦截.
单飞行器拦截目标动态分配算法流程: 单个飞行器在初始时刻判断对抗场景中红方本体个数, 若红方个数为1,则直接拦截,不需要进行目标分配;若飞行过程中探测到的红方实体个数发生改变(诱饵数量增加),则先对飞行器进行甄别,若识别出其为诱饵,则威胁值为0,若未识别出则进行态势估计,将结果传递给指挥决策层. 决策层整合各飞行器威胁估计结果,使用目标分配算法,将分配结果发送给各个飞行器,飞行器接收相应指令进行拦截.
3 红方飞行器博弈算法设计
采用改进的深度确定性策略梯度(deep deterministic policy gradient,DDPG)算法对飞行器攻防对抗场景中的逃逸方(红方)进行训练, 使红方智能体采取最优策略躲避蓝方多个飞行器的拦截. 在传统DDPG 方法的基础上,提出一种基于先验知识(prior knowledge)的DDPG 算法即DDPG-PK 算法. 在动作选择时,根据专家经验加入先验知识(动作选择时受规则限制),并在采样时根据样本权重优先选取价值高的样本,利用神经网络进行预训练.
3.1 红方飞行器的MDP 模型
马尔科夫决策过程(markov decision process,MDP)可由包含状态空间、动作空间、状态转移函数、回报函数、折扣因子的五元组描述[19]. 针对红蓝双方典型的对抗场景,建立的MDP 模型如下.
对于红方飞行器而言, 目的是躲避蓝方多个飞行器的拦截, 红方的策略是优先躲避对自己威胁最大的蓝方飞行器, 故红方选择与其距离最近的蓝方,记录其编号,计算红蓝的相对距离、视线高低角和方位角. 采用红蓝双方的三维位置建立MDP 状态空间,为增强算法泛化性, 采用红蓝双方的相对位置关系,给出的状态空间如下:

式中,R为红方和蓝方的相对距离,qε为红方与蓝方视线的高低角,qβ为视线方位角.
对于追逃博弈场景,MDP 转移函数为各智能体的运动学方程.
训练目标: 训练红方在合适姿态下释放较少的诱饵且机动时间尽可能少(节省燃料)时成功逃逸.
红方携带诱饵数量为n,每一时刻对每个诱饵可选择抛撒或不抛撒策略,可进行姿态调整,也可选择机动.因此,设计的动作空间为:
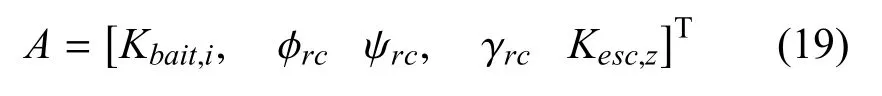
式中,Kbait,i为红方释放第i个诱饵的指令,φrc、ψrc、γrc为红方姿态调整指令,Kesc,z为红方机动指令,Kbait.i、kesc,z∈{−1,0,1}.
在蓝方多个飞行器拦截红方一个飞行器的对抗场景下, 红方释放诱饵个数需尽量大于蓝方飞行器数量, 若红方释放诱饵时机合理且合适的姿态调整使得抛撒诱饵的方向也合理, 则抛撒的诱饵对蓝方飞行器产生较高的欺骗性,后续博弈过程中,红方再结合机动变道才能有效躲避蓝方多个飞行器拦截.红方需选择最优策略,朝合适的方向抛诱饵,抛出数量尽可能少, 机动时间尽可能少, 以保存实力, 故设定MDP 奖励函数为:

式中,resbait为红方剩余诱饵个数. 初始resbait为红方携带诱饵总数, 每抛出一个诱饵resbait−1;restime表示剩余机动时间,初始为红方可机动的总时间,每步机动一次, 则restime−0.01;tbait,i为释放第i个诱饵的时刻.rwd1为机动指令即时奖励, 有机动动作时给一定惩罚, 没有时给出奖励, 目的是节省燃料;rwd2为抛诱饵指令即时奖励, 过早抛诱饵时给出惩罚,抛诱饵时刻晚时获得较高奖励. 只在抛诱饵的时刻计算此奖励, 并将此时刻抛出全部诱饵的奖励累加计算.
3.2 改进的DDPG 算法设计
红方飞行器姿态变化是连续动作, 所以选择具有连续动作空间的DDPG 算法. 但是传统的DDPG算法存在动作难探索到较大奖励、收敛速度较慢等问题, 可在采样方法、动作噪声设计、分布式并行计算、经验回放机制等方面对DDPG 算法进行改进[19−23]. 除上述方法,加入先验知识也可加快深度强化学习方法学习速度,缩短算法收敛时间[24−27].
结合红蓝对抗场景, 考虑红方飞行器携带3 个诱饵时, 其七维的动作空间探索难度较大, 所以, 选择先验知识和优先权重相结合的方式优化算法. 引入专家的先验知识,缩小智能体的决策空间,对神经网络进行预训练,同时在进一步提升收敛速度,提高样本利用率的同时增强样本相关性, 采用具有优先经验回放的DDPG 进行预训练.

图1 蓝方单飞行器动态目标分配流程图Fig.1 Blue single aircraft dynamic target allocation fl w
在简单环境下进行100 次预训练, 如图2 所示.简单环境指的是对于红方飞行器而言, 动作空间较小、容易学习到较优的策略环境,如不考虑姿态调整和机动调整策略,可抛撒诱饵的时间变短等. 简单环境中加入专家的经验知识, 经验知识即在红蓝相距更近距离(R< 20 km)后释放诱饵,以规则形式限定智能体的动作选择,以此加入训练环境中,将这些专家经验存储在经验池中. 此环境下预训练场景中得到的actor 和critic 网络称为预训练网络, 将预训练网络和经验池中的专家经验统称为预训练知识, 作为再训练环境的输入,如图3 所示. 再训练环境为更复杂的环境,即在满足红方飞行器探测距离后,红方就可进行决策, 包括可采取机动动作、抛诱饵和姿态调整,动作维度由三维上升到七维,动作空间大小由31300变为71200,训练难度大大增加. 训练样本有30%基于先验知识生成, 70%利用强化学习算法进行训练. 逐步减小基于先验知识的样本比例,最终样本全部通过强化学习得到, 保存训练后的神经网络,进行测试. 再训练初期记忆回放单元中存储大量具有先验知识的样本,随着训练不断进行,样本不断更新,最终全部成为强化学习产生的样本. 算法如表1所示.
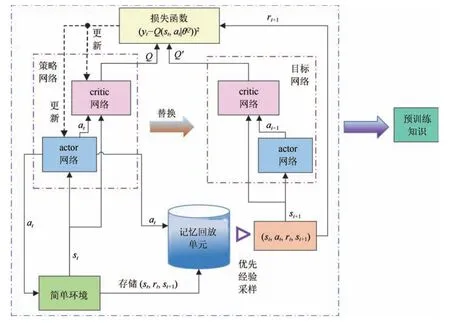
图2 DDPG_PK 预训练算法框架Fig.2 DDPG_PK pre-training algorithm structure
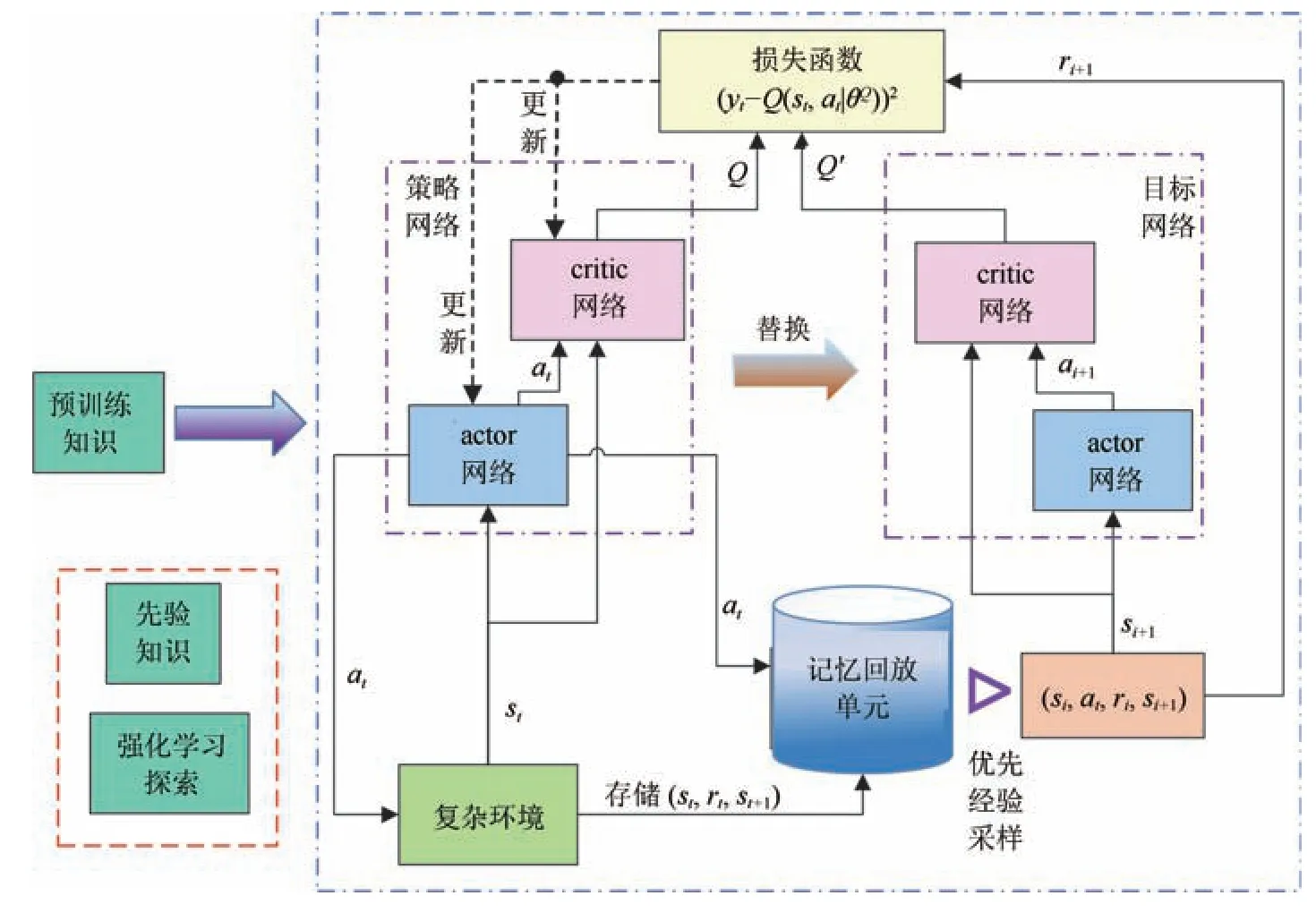
图3 DDPG_PK 再训练算法框架Fig.3 DDPG_PK retraining algorithm structure

表1 DDPG_PK 多飞行器追逃博弈算法Table 1 DDPG_PK multi-aircraft pursuit-evasion game algorithm
4 仿真验证与分析
设定红方飞行器质量为100 kg, 可用推力2 000 N; 蓝方飞行器质量均为20 kg, 最大可用过载4 g,蓝方采用比例导引法拦截红方,比例导引系数均为3. 仿真步长为0.01,总仿真时间20 s,积分环节采用四阶龙格库塔法. 红蓝双方初始位置和速度具有一定随机性.
在不同仿真场景的博弈过程中, 红方分别采用固定策略和智能策略. 蓝方面对红方多个飞行器时(含诱饵和红方飞行器本体),利用匈牙利算法进行目标分配, 选择最佳拦截目标, 完成拦截任务. 博弈过程体现在红方在约束条件下选择何时抛诱饵或机动或姿态调整, 蓝方面对红方多个本体(含诱饵)如何选择目标进行拦截.
红方逃逸成功标志为所有蓝方均拦截诱饵, 或者仿真时间结束时红方与所有蓝方的视线离轴角η > 60°,此时红方超出蓝方探测范围.蓝方拦截成功标志为蓝方有一个飞行器击中红方, 蓝方击毁条件即红蓝双方相对距离小于R< 100 m且视线离轴角η < 20°. 若仿真结束时,红方未被拦截则红方逃逸成功. 实验设定红蓝相对距离R< 30 km 后,红方可见蓝方, 可采取各种决策; 蓝方全程可知红方位置, 但初始感知噪声为位置噪声3 000 m,速度噪声120 m/s.红方最大可机动时间为1.5 s.
4.1 目标分配算法验证
以红方携带3 枚诱饵为例,对目标分配算法进行验证. 整个博弈过程蓝方进行多次目标选择,初始时刻,蓝方两个飞行器选择拦截红方本体,红方抛出诱饵后,蓝方再次进行目标选择,若红方抛出3 枚诱饵且欺骗蓝方成功, 则蓝方两个飞行器分别选择4 个目标中的两个进行拦截. 红方及诱饵被击中一次即损毁.
初始位置及速度如表2 所示, 其余参数假设为psc= 1,pnc= 0.35 −0.95,d1= 20 km,d2=40 km,p1= 0.95,p2= 0.35,σR=Rmin+Rmax,nc=1.0,nd= 0.5,C1= 0.4,C2=C3= 0.3,Rmin=1 km,Rmax=60 km.

表2 实验初始参数设定Table 2 Experiment initial parameter setting
若红方飞行器在29 km 抛出3 个诱饵,得到红蓝威胁矩阵为:

利用匈牙利算法得到的目标分配矩阵α 为:

此时,蓝方2 号选择拦截红方,蓝方1 号选择拦截红方1 号诱饵,在此时刻,虽然红方抛出3 个诱饵,但是诱饵产生的威胁值过小, 没有引诱全部蓝方进行拦截.
若红方飞行器在19 km 抛出3 个诱饵,得到红蓝威胁矩阵为:

利用匈牙利算法得到的目标分配矩阵α 为:

根据分配结果蓝方两个飞行器均选择拦截红方诱饵,红方可以成功逃逸,此时的红方策略更优.
两次分配红方集群威胁值分别为1.056 02、1.608 97, 均大于随机选择威胁值. 上述结果表明,所使用的匈牙利算法分配可以找到红方集群威胁值最大的最优解.
4.2 DDPG_PK 算法验证
4.2.1 仿真场景设置
仿真场景选取传统策略和智能博弈对抗策略进行比较验证,选用4 个仿真场景如下:
仿真场景1: 基于固定策略:设定红方飞行器在红蓝相距29 km 处释放全部诱饵,在燃料剩余的情况下随机选择机动动作.
仿真场景2: 基于智能策略:神经网络模型初始参数随机设定, 用初始设定的神经网络模型直接控制红方飞行器决策.
仿真场景3: 基于智能策略:无先验知识直接训练时的利用神经网络控制红方飞行器决策.
仿真场景4: 基于智能策略:利用先验知识训练后的神经网络控制红方飞行器决策.
仿真场景1 中,飞行器策略是固定的,不管在对抗环境中遇到何种情况, 飞行器均采取已设定好的策略, 其面对动态变化的蓝方多个飞行器拦截易处于劣势,很多情况下难以逃逸成功. 仿真场景2、3、4中飞行器根据当前探测到的蓝方信息(包含位置、速度等), 分别通过初始神经网络、无经验知识训练的神经网络、利用先验知识训练后的神经网络决定此时策略(是否抛诱饵、机动、姿态调整),躲避蓝方拦截. 利用神经网络决策的飞行器面对复杂动态变化的对抗环境时能实时进行决策, 不受固定策略限制,更易完成逃逸任务.
4.2.2 实验参数设置
实验采用DDPG PK 算法进行训练, 算法中网络均为全连接网络的架构, actor 网络有2 个隐含层, critic 网络有一个隐含层, 均是反向传播(back propagation, BP)神经网络结构. 训练算法的学习率actor 网络为0.000 2, critic 网络为0.000 5, 折扣因子为0.999, 经验池为200 000, batch_size = 64, 加入动作噪声增加探索性, 初始动作噪声为3, 随后逐渐减少至0.1. 实验首先选取的对抗环境实验1 为蓝方两个飞行器拦截红方一个飞行器, 而后进行更多飞行器的对抗实验.
4.2.3 实验结果分析
使用传统的DDPG 方法直接训练神经网络, 智能体能探索到较大奖励,但经常失败,算法无法收敛.采用本文提出的DDPG_PK 算法基于先验知识进行预训练, 将预训练好的神经网络放入环境中继续训练. 接下来验证算法一致性,修改随机种子进行多次训练, 阴影区域表示训练过程中智能体得到的最大奖励和最小奖励区域.训练结果如图4 所示, 前100次为预训练, 具有先验知识的智能体可以获得较大奖励,后900 次是规则加强化学习混合训练,智能体经过短暂的探索后收敛到较大奖励,选择10 次事件的平均奖励作为结果展示.
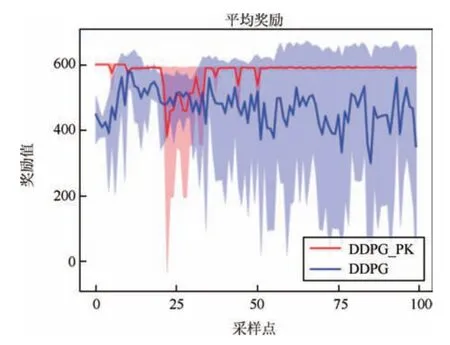
图4 训练1 000 回合平均奖励Fig.4 Average reward of training for 1 000 episodes
图5 展示了基于先验知识的红蓝双方的轨迹图,具有一定经验的智能体选择策略合理, 先验知识中未添加机动和姿态调整策略, 故智能体只选择在红蓝距离19 km 处释放3 个诱饵, 诱饵成功诱惑蓝方,红方面对蓝方多个飞行器成功逃逸.

图5 基于先验知识的红蓝飞行器轨迹图Fig.5 Red and blue aircraft trajectories based on prior knowledge
图6 展示红方未选择抛诱饵策略, 只进行机动和姿态调整,未能躲避蓝方拦截;图7 红方虽然抛出3 个诱饵,但未能迷惑蓝方或者蓝方根据目标分配算法仍然选择威胁值较大的红方拦截. 由图6、图7 可见,训练前红方抛诱饵时机、数量或者姿态调整及选择机动动作不合理,很容易被蓝方多个飞行器拦截.

图6 训练前红蓝飞行器轨迹图(无诱饵)Fig.6 Red and blue aircraft trajectory before training(without bait)

图7 训练前红蓝飞行器轨迹图(包含诱饵)Fig.7 Red and blue aircraft trajectory before training(including bait)
图8 展示了训练中期智能体学习到逃逸成功的策略, 但此时机动时间长, 耗费燃料多, 得到奖励较小. 图9 展示了训练后红方智能体选择最佳的逃逸策略,进行适当的姿态调整,在红蓝距离较近时红方抛出3 个诱饵且机动较少. 各仿真结果的抛诱饵时机、数量、机动时间如表3 所示,姿态调整策略如图10 所示.
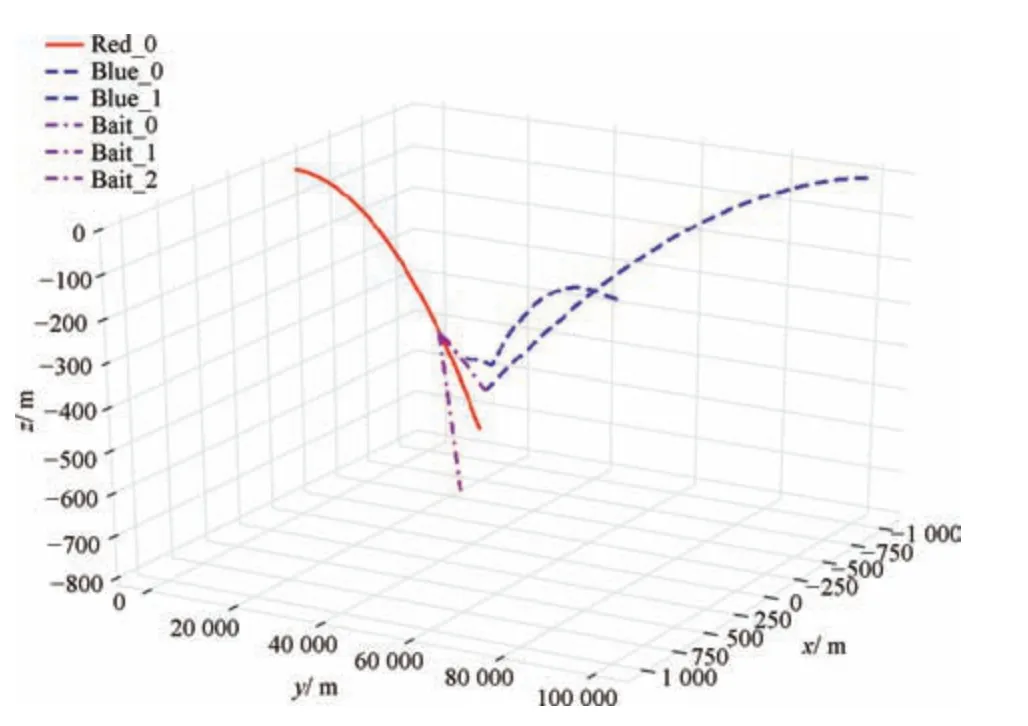
图8 训练中红蓝飞行器轨迹图Fig.8 Red and blue aircraft trajectories during training

图9 训练后红蓝飞行器轨迹图Fig.9 Red and blue aircraft trajectory after training
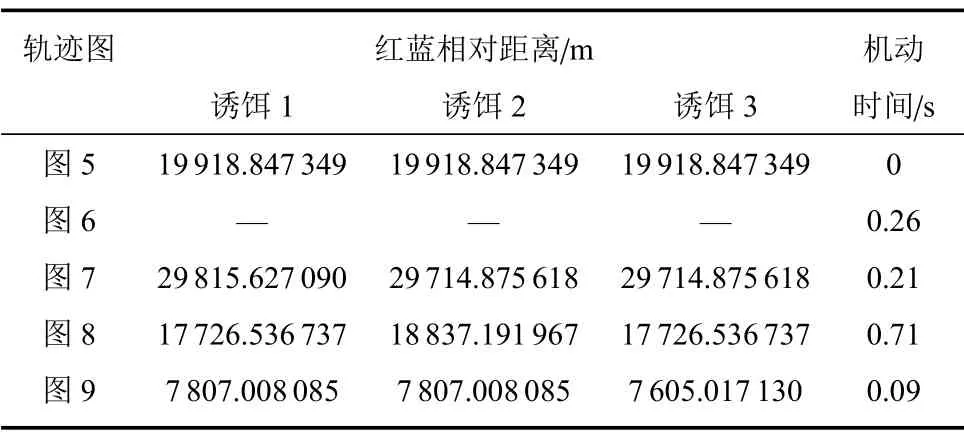
表3 训练前后红方飞行器策略对比Table 3 Comparison of Red aircraft strategy before and after training
图10 中的仿真结果表明所提出的DDPG_PK 算法相比于传统的DDPG 算法能很快收敛, 智能体较快学习到成功逃逸的策略.
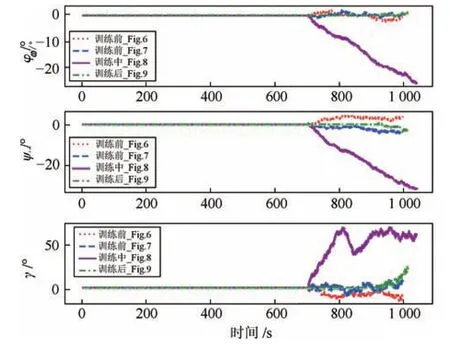
图10 各场景飞行器姿态变化图Fig.10 Aircraft attitude changes in various scenarios
实验1 首先对训练好的模型进行测试, 并将训练前后结果及传统固定策略逃逸成功结果进行对比.实验1 中仿真共选取4.2.1 节4 个场景进行对比验证. 训练结果见表6, 结果表明使用DDPG_PK 算法训练的网络在测试中逃逸成功率高达97%以上, 可以很好地控制飞行器完成逃逸任务.
4.2.4 算法拓展性仿真验证
将此方法拓展于更多数量的飞行器博弈对抗场景. 用实验1 的训练方式继续训练红方智能体, 让红方携带更多诱饵,抵御更多蓝方飞行器的拦截. 设置实验场景2 ~5 分别为红方携带4 个诱饵,对抗蓝方3 个飞行器(初始队形为横向编队、三角形编队);红方携带5 个诱饵,对抗蓝方4 个飞行器(初始队形为横向编队、菱形编队). 其中, 抛诱饵时机、数量、机动时间等训练结果如表4 所示, 蓝方飞行器初始位置如表5 所示,其余参数均与实验1 设定相同,各实验场景训练后红蓝飞行器轨迹图如图11 ~图14所示.

表4 各实验红方飞行器策略对比Table 4 Comparison of red aircraft trajectories in various scenarios

表5 各实验蓝方初始位置(xb,yb,zb)参数设定Table 5 Blue initial position(xb,yb,zb)parameter setting in various scenarios

图11 飞行器1(4)V3 横向编队轨迹图Fig.11 Horizontal formation trajectories of aircraft 1(4)V3
图11 ~图14 展示了红方携带更多诱饵与蓝方多个飞行器博弈场景. 可以看出蓝方初始队形为横向、三角形或者菱形编队, 飞行器数量由2 扩展到4,所提出方法均使得红方智能体学习到逃逸策略,且所用机动时间较少. 将每个实验同样在4 个场景中进行对比验证,仿真结果如表6 所示,结果表明所提出的DDPG_PK 算法可应用于多个飞行器博弈对抗场景, 相比基于固定规则和无规则训练的方法进行博弈对抗,其逃逸成功率均有显著提升.
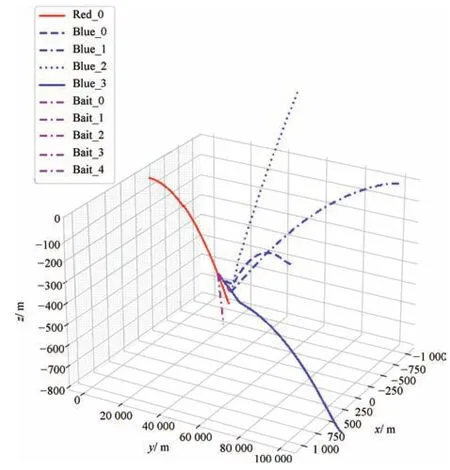
图14 飞行器1(5)V4 菱形编队轨迹图Fig.14 Diamond formation trajectories of aircraft 1(5)V4

表6 各场景实验逃逸成功率比较Table 6 Comparison of experimental escape success rates in various scenarios

图12 飞行器1(4)V3 三角形编队轨迹图Fig.12 Triangle formation trajectories of aircraft 1(4)V3

图13 飞行器1(5)V4 横向编队轨迹图Fig.13 Horizontal formation trajectories of aircraft 1(5)V4
5 结论
通过对高速飞行器的博弈对抗仿真, 证明飞行器采取抛诱饵、姿态调整、机动调整等策略可有效躲避蓝方多个飞行器动态拦截. 针对多飞行器拦截多个目标问题,采用匈牙利算法进行动态目标分配,实现对红方飞行器集群最大程度打击. 采用改进的DDPG 算法—DDPG_PK 算法,用先验知识进行预训练和采用优先经验回放机制相结合的方式, 可以加快智能体学习速度和算法收敛速度, 有效地解决了多拦一场景下飞行器难以逃逸的问题. 与传统固定抛诱饵策略相比,智能体逃逸成功率显著提升. 利用本文所提算法, 使红方飞行器与不同编队及不同数量的蓝方飞行器对抗, 均能获得较高的逃逸成功率,验证该算法具有一定的泛化能力. 所提方法对研究高速空间飞行器群体博弈策略有较强的借鉴意义,可将此方法拓展于更复杂的飞行器博弈对抗场景.
