基于高光谱的油菜叶片SPAD值估测模型比较
2021-02-12王克晓
王克晓,周 蕊,李 波,欧 毅,黄 祥,虞 豹
(重庆市农业科学院农业科技信息研究所,重庆 401329)
0 引言
【研究意义】叶绿素与植物光合作用能力和生长状况紧密相关,是植物氮含量重要的指示器[1-2]。在实际研究和应用中,常采用SPAD值来表征植物的叶绿素含量[3]。【前人研究进展】近年来,随着高光谱遥感技术的发展,衍生了大量的光谱特征参数,为定量探测作物关键农学指标提供了有效途径[4-5]。基于光谱技术的叶片SPAD值测定方法逐渐成为作物叶绿素含量定量化诊断的有效手段,广泛应用于玉米、小麦、水稻及油菜等作物的叶绿素含量检测中[6-7]。Horler等[8]通过研究植被反射光谱与叶绿素含量的关系,提出了光谱“红边”参数在植被叶绿素含量估测中的作用。Daughtry等[9]通过研究玉米叶片叶绿素含量与光谱波段、光谱指数的关系,构建玉米叶绿素含量估测模型。Broge等[10]分析不同氮素水平下的小麦冠层光谱数据,提出比值植被指数RVI能够有效地预测冠层叶绿素的含量。姚付启等[11]分析了梧桐叶绿素含量水平与10种植被指数的相关关系,认为植被NDVI与叶绿素含量的关系最为密切。在模型预测方面,孙明馨等[12]基于拔节期冬小麦高光谱与SPAD值关系,选用不同光谱参数特征构建了冬小麦SPAD值的指数、对数等函数回归模型。赵琨等[13]通过对不同氮素水平下的油菜植株不同叶位叶片的高光谱数据处理,对基于偏最小二乘和最小二乘-支持向量机的SPAD预测模型进行了对比。由明明等[14]基于油菜不同生育期光谱指数构建了叶片SPAD值随机森林估测模型。崔小涛[15]通过筛选油菜叶片SPAD敏感光谱参数,构建了基于光谱参数的单因素模型、偏最小二乘回归模型和多元线性逐步回归遗传算法优化的单隐层BP神经网络SPAD估测模型。李媛媛等[16]通过分析玉米乳熟期叶片的一阶微分光谱、高光谱特征参数与对应叶片SPAD值的相关关系,构建了基于一阶微分光谱、高光谱特征参数和BP神经网络的玉米叶片SPAD估算模型,并将BP神经网络模型与主成分回归、偏最小二乘回归以及传统回归模型进行了比较。【本研究切入点】以往诸多研究中大多是基于光谱特征参数及各种植被指数通过统计回归或者浅层机器学习等方法对作物叶片进行叶绿素含量预测[17],较少涉及有深度学习算法参与的不同估测模型在油菜叶片叶绿素含量SPAD值估测模型中的比较分析。【拟解决的关键问题】以现蕾期油菜叶片为研究对象,基于光谱反射特征和光谱参数与SPAD值的相关性进行光谱参数筛选,并构建了偏最小二乘回归(Partial Least Squares Regression,PLSR)、传统反向传播神经网络(Back Propagation Neural Net,BPNN) 、支持向量回归(Support Vector Regression,SVR)和深度神经网络模型(Deep Neural Net,DNN)等不同估测模型,探索不同估测模型在油菜叶片SPAD值估测中的应用效果,为光谱探测油菜叶片叶绿素含量提供参考。
1 材料与方法
1.1 叶片SPAD值测定
在种植同一品种的同一地块内随机均匀选择60棵生长健康的现蕾期油菜植株,每颗植株上任意选择1片上层基生长柄叶,共计60片。单个叶片上的SPAD值采集点分别位于避开叶脉的3个随机部位,取其SPAD均值作为该叶片的最终SPAD值。叶片SPAD值的采集通过FK-YL04型手持式叶绿素仪测定完成,通过其配套工具软件将其采集结果导出为Excel文件,并通过Excel 2010完成单个叶片不同部位SPAD值的均值化过程,最终形成60个油菜叶片SPAD值的样本数据集。
1.2 叶片高光谱数据采集与处理
叶片高光谱数据的采集与油菜叶片SPAD值测定同步进行。采用美国ASD公司的Field Spec Handheld 2手持地物光谱仪,光谱采集范围325~1075 nm,波长间隔1 nm。利用其叶片夹及其自带光源测定采样部位的高光谱信息,每个叶片上3个采集点位,每个采样点记录3条光谱,取均值作为该叶片的最终光谱曲线,并通过Origin 9.0对光谱曲线进行Savitzky-Golay卷积滤波平滑处理。为能较好地保留光谱数据的原始特征,平滑参数设置为窗口点数35的2阶多项式。为提高精度,截去容易出现较大噪声的325~400 nm的蓝紫光和1000~1075 nm的短波近红外波段,留用400~1000 nm的光谱范围进行研究。
1.3 光谱参数选择与计算
油菜叶片样本在400~1000 nm反射光谱曲线与SPAD值的Pearson线性相关关系如图1所示。可见光-红边范围内,叶片SPAD值与光谱曲线在425~495 nm的蓝波和665~680 nm的红波区域呈现微弱正相关,而在510~650 nm的绿、黄波段和690~735 nm的红边波段在0.01显著性水平下呈显著负相关性。因此,本研究以上述具有显著相关性的波段参与定义或计算为基础确定所采用的光谱参数,主要包括高光谱位置特征、面积特征以及植被指数等3类共计13个光谱参数(见表1)。
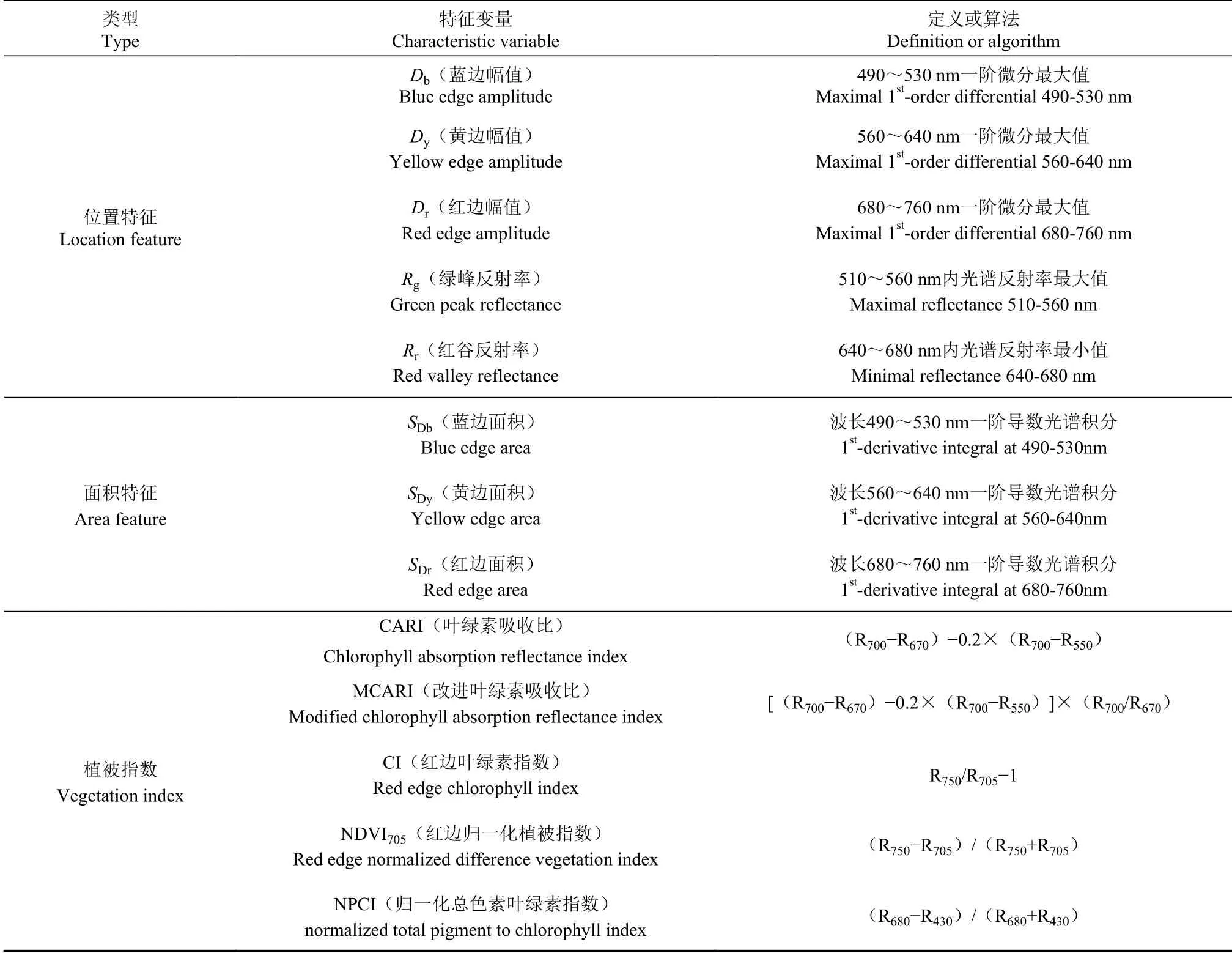
表1 光谱参数及其定义或计算公式Table 1 Spectral parameters and definitions or calculation formula
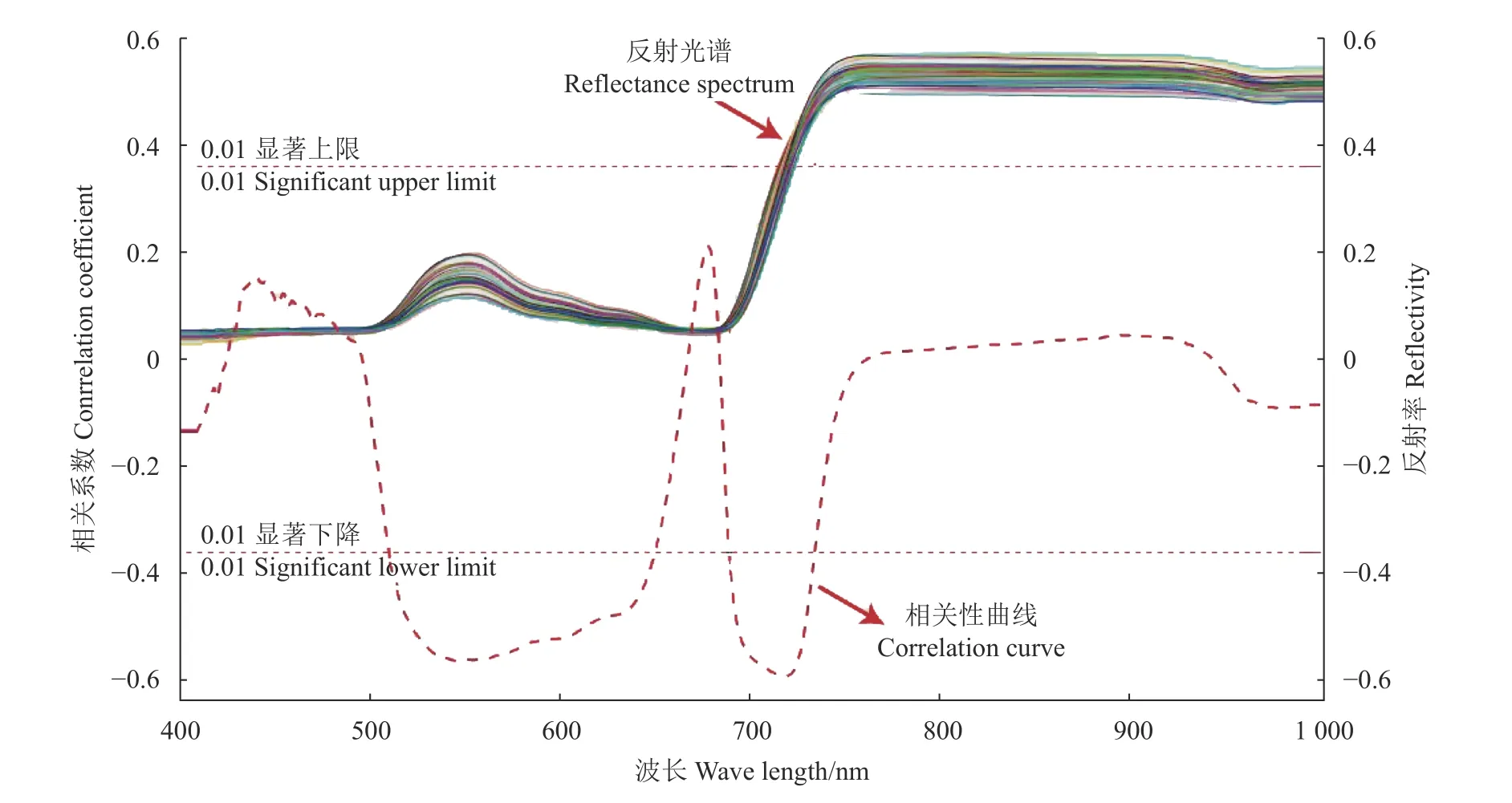
图1 叶片光谱与SPAD值相关性Fig. 1 Correlation between spectra and SPAD of leaves
1.4 基于相关分析的光谱参数优化
现蕾期油菜叶片光谱参数与SPAD值的相关性见图2。在所选的13个光谱参数中有9个光谱参数在0.01的检验水平中呈现显著相关性。其中,位置特征参数中,Rg与Db、Dr的相关性分别为0.89和0.72,但与Dy的负相关系数为-0.34。面积特征参数中,SDb与SDy呈现的相关性高达-0.98,但与SDr的相关性相对较弱,相关值-0.37。植被指数参数中,CARI与MCARI、CI与NDVI705两组光谱参数的正相关系数分别高达0.99。在光谱参数与叶绿素SPAD值的相关性方面,SDb和SDy两个光谱参数对SPAD值的影响表现恰好相反,但考虑到两者间较强的相关性,因此两者在模拟现蕾期油菜叶片叶绿素SPAD值时具有可互相替代性。另外,满足上述可互相替代性的还有CARI与MCARI、CI与NDVI705两组光谱参数。同时,与叶绿素SPAD值显著相关的参数还有Db、Dr与Rg,负相关性均在0.5以上。另外,Dy、Rr、SDr和NPCI等4个特征参数与叶片叶绿素SPAD值的显著不相关间接也说明了叶片在蓝波和红谷波段处的反射率与SPAD值之间的线性弱相关,这与图1所示内容相一致。基于上述分析,本研究保留Db、Dr、Rg、SDb、CARI和CI等6个光谱参数作为SPAD值估测的特征变量以便后续估测模型构建应用。
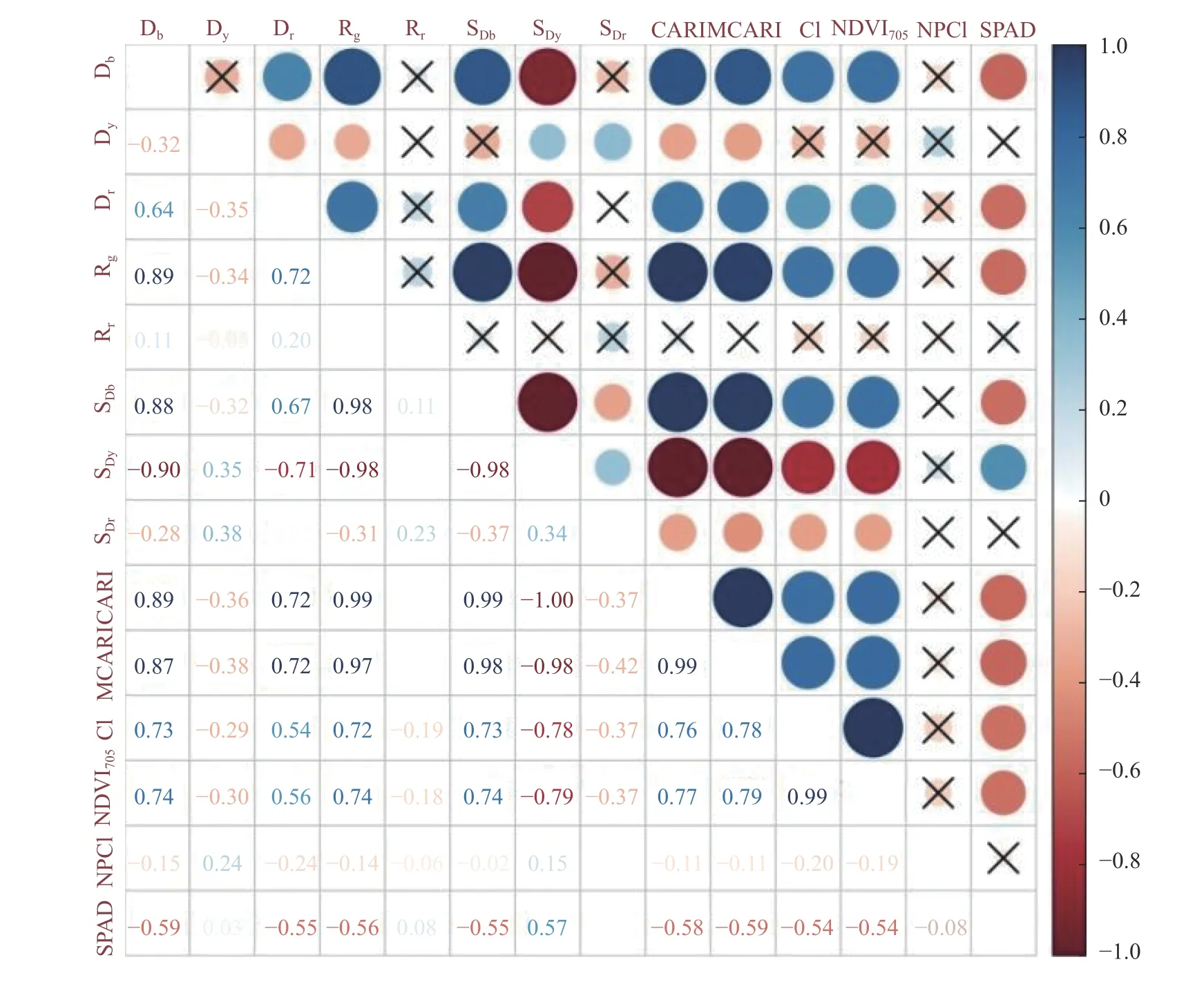
图2 光谱参数及与SPAD值的相关性Fig. 2 Correlation between spectral parameters and SPAD
1.5 估测模型及精度检验方法
在采样样本数据中,随机选取70%作为训练集,30%作为测试集,基于训练集构建偏最小二乘回归(PLSR)、BP神经网络(BPNN)、支持向量回归(SVR)和深度神经网络(DNN)等模型对油菜叶片叶绿素SPAD值进行估测研究,并利用测试数据集对SPAD值反演模型进行精度评定。估测模型评价指标采用能够反映模型稳定性的决定系数R2、反映模型预测能力的均方根误差RMSE和相对分析误差RPD等3个指标[18]。其中,RPD为样本标准差与预测均方根误差的之比,RPD≥2说明模型具有极好的预测能力;当1.4≤RPD<2时,说明模型效果一般,可对样本进行粗略估计;RPD<1.4则说明模型效果较差。测试样本预测性能通过R2和RMSE两项指标进行检验。以上估测模型的构建通过R语言实现,检验指标通过Excel 2010计算完成。
2 结果与分析
2.1 PLSR模型构建与检验
PLSR集中了主成分分析、典型相关分析和普通多元线性回归等方法的优点,能够在严重相关的特征变量中有效地筛选出对因变量有较强解释性的光谱参数变量,同时避免了建模过程中的过拟合问题,具有较好的泛化能力[19]。以上述筛选的6个光谱参数为特征变量,叶片SPAD值为响应变量,基于R语言pls工具包的Jackknife抽样方法和Leaveone-out交叉验证法确定回归模型中最佳主成分因子数,利用widekernelpls算法建立PLSR模型。当主成分因子数ncomp设定为2时,训练样本预测均方根误 差(Root Mean Squared Error of Prediction,RMSEP)达到最小1.8。
PLSR模型训练样本拟合结果和测试样本的预测结果如图3所示,训练样本的R2为0.66,RMSE为1.76,RPD为1.69;测试样本的R2为0.63,RMSE为1.77。

图3 叶片SPAD值PLSR模型Fig. 3 PLSR model of leaf SPAD
2.2 BPNN模型构建与检验
BP神经网络是一种按照预测误差逆向传播来调整输入与输出神经元之间权值的前馈式多层感知机,包括正向预测结果计算和逆向误差传回两个过程。RSNNS是基于德国斯图加特大学开发的神经网络仿真软件SNNS的R包,包含了多种神经网络模型函数。本研究中的BP-NN模型主要基于RSNNS工具包构建,学习算法选择“Std_Backpropagation”,设置的两个隐层神经元节点数均为5,激活函数为sigmoid 函数,学习率为0.1,误差反馈限差为0.2。
基于BPNN的叶片SPAD预测模型训练样本的R2为0.73,RMSE为1.58,RPD为1.89;测试样本的R2为0.70,RMSE为2.02。模型估测效果比PLSR有所提升。
2.3 SVR模型构建与检验
SVR是基于统计学习理论提出的一种新的机器学习方法,具有良好的泛化能力,已广泛应用于小样本学习问题[20]。本研究基于R语言e1071工具包构建SVR模型,采用ε-SVR支持向量回归,ε参数默认为0.1,核函数类型默认为径向基函数(Radical Basis Function,RBF),利用tune函数进行参数优化,采样方法采用5折交叉验证,确定训练样本最优参数为Gamma=0.0001,Cost=88。
SVR模型训练样本的R2为0.80,RMSE为1.39,RPD达到2.14;测试样本的R2为0.69,RMSE为1.57。SVR模型在训练样本的稳定性和预测能力有较大提高。
2.4 DNN模型构建与检验
H2O是一种开源的,分布式的且可扩展的快速机器学习平台,能够支持深度学习(Deep Learning),梯度推进机(Gradient Boosting),随机森林(Random Forest),广义线性建模(Generalized Linear Modeling),支持向量机(Support Vector Machine)和自动机器学习(Automatic Machine Learning)等一系列机器学习[21]。其中的深度学习算法框架不同于传统BP神经网络神经元节点权重调节方法,而是通过基于随机梯度下降的分布式多线程训练、精调等过程实现节点权值调整[22]。本研究主要通过H2O平台构建了双隐层深度神经网络学习模型,激活函数采用默认的“Rectifier”函数,训练样本采用5折交叉验证。为防止训练过程过拟合,采用提前终止策略,具体深度神经网络算法参数见表2。

表2 深度神经网络算法参数Table 2 Parameters applied for deep neural network algorithm
DNN模型训练样本拟合结果和测试样本的预测结果如图4所示,训练样本的R2为0.93,RMSE为0.77,RPD提高到3.92;测试样本的R2为0.78,RMSE为1.78。上述指标说明DNN模型具有极好的预测能力。
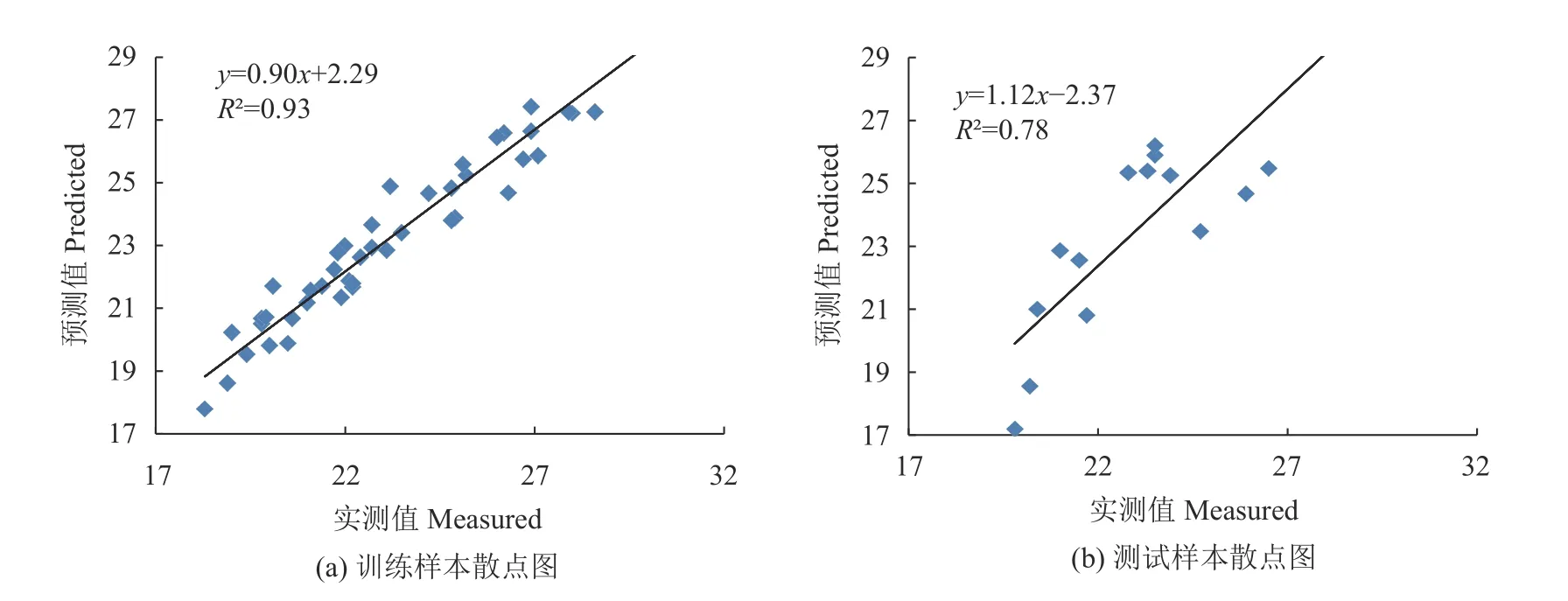
图4 叶片SPAD值DNN回归模型Fig. 4 DNN model on rape leaf SPAD
2.5 不同估测模型效果对比分析
各模型精度对比如表3,可以看出,DNN模型决定系数R2最大为0.93,且RPD最高3.92,说明具有较好的预测能力,其次是SVR模型;而PLSR和BPNN模型R2中等且RPD处于1.4~2.0,可以对样本进行粗略估计。在测试样本精度方面,测试样本R2变化趋势基本与训练样本变化一致,DNN的R2比SVR高。RMSE比SVR略低。上述对比结果表明,在本研究相对较小样本条件下,支持向量回归SVR和深度神经网络DNN在油菜叶片叶绿素SPAD值训练样本拟合和测试样本检验等方面都具有相对较好的估测能力,且DNN模型的稳定性和估测能力更好。
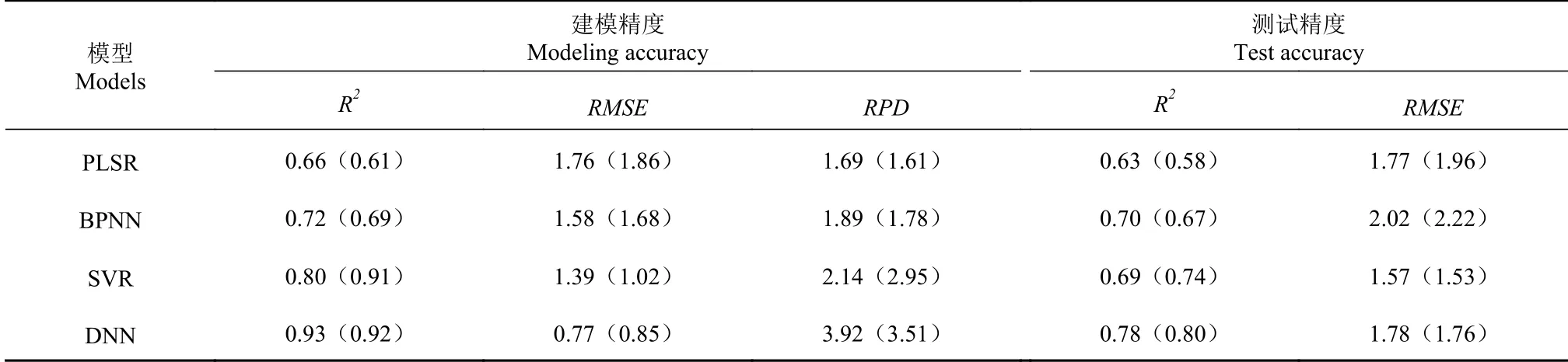
表3 不同模型精度比较Table 3 Accuracy of models
另外,由表3中对应模型的相应指标对比可知,特征变量优化后的PLSR、BPNN和DNN等三种模型建模精度在各个方面均有所提升。其中,PLSR模拟效果提升较大,可能是因为偏最小二乘拟合方法本身就是线性回归的本质,与基于线性相关的特征优化方法有密切关联,而基于神经网络的BPNN和DNN模型精度受影响相对较小。SVR模型的精度稍有下降,但整体上仍具有较好的预测能力。
3 讨论与结论
(1)现蕾期油菜叶片SPAD值与原始光谱在425~495 nm的蓝波、665~680 nm的红波区域呈现微弱正相关,并在508~650 nm的绿、黄波段和688~735 nm的红边波段在0.01显著性水平下呈显著负相关性,验证了红、绿光谱特性以及“红边”波段在植被叶绿素含量探测中的有效性,与Horler的相关结论相一致[8]。
(2)特征变量相关性分析表明,SDb与SDy线性负相关性-0.98,CARI与MCARI、CI与NDVI705两组光谱参数内指标间的线性正相关系数为0.99。同时,SDb与SDy、CARI与MCARI、CI与NDVI705等三组光谱参数与油菜叶片SPAD值均线性显著相关,说明上述每组参数内的两个指数在模拟叶片叶绿素SPAD值时可互相替代。同时不同模型估测结果表明,光谱特征优化不仅可以减少不必要的变量冗余,还有助于提高估测模型预测精度,与刘宁关于叶绿素检测光谱变量筛选讨论结果一致[23]。
(3)徐逸等在利用HJ-1B卫星CCD多光谱波段组合分别构建随机森林RF、SVR、BPNN和DNN等四种模型反演太湖叶绿素a浓度时,从模型精度、稳定性和鲁棒性等方面验证了DNN模型在叶绿素浓度反演中的巨大应用潜力[24]。本研究中的4种模型的建模及样本测试精度也表明:基于机器学习的估计预测模型比传统线性回归具有较高的稳定性和预测能力,深度学习算法在油菜叶片叶绿素SPAD值训练样本拟合和测试样本检验等方面具有更好的估测能力,与其研究结论相一致。
(4)本研究以现蕾期油菜叶片叶绿素SPAD值为估测对象,利用R2、RMSE和RPD等3个指标检验了较少样本条件下基于筛选的6个光谱参数建立的偏最小二乘线性回归PLSR、BP神经网络回归BPNN、支持向量回归SVR和深度学习DNN等非线性模型的模拟能力。然而,本研究是通过Pearson线性显著性相关分析筛选构建模型所需的光谱参数,对于在大量样本支持下引入更多SPAD值敏感的非线性光谱变量的条件下,上述各种预测模型的相对效果有待进一步分析。
(5)利用叶绿素含量和高光谱反射率的关系,建立基于叶片光谱的SPAD值估算模型是可行的。BP神经网络能够较好地解决非线性拟合问题,比PLSR模型具有更好的预测效果,但不如SVR模型,可能与构建神经网络时设置的训练参数有关[25]。而在不同的生育阶段,因作物叶片光谱与SPAD值的显著相关性以及构建的高光谱特征参数各不相同,使得不同生育期反演油菜叶片SPAD值的回归模型各不相同[16]。本研究结果表明,同一生育期不同建模方法对估算模型预测精度的影响也较大,非线性的叶片SPAD值估测模型精度更加可靠,而基于深度学习的DNN模型具有更好的估测能力,但对于其他生育阶段的普适性也有待进一步验证。
