基于F-M II 状态空间模型的多维系统实现方法①

陈君昊 程 骅 刘惠康 盛道清

(武汉科技大学信息科学与工程学院 武汉430080)

0 引言

随着计算机技术和工业过程控制的快速发展,在一些实际工程领域中多维变量系统的应用越来越广泛,如机械故障检测、板材成形、卫星云图、地震数据处理和图像处理等领域[1-2]。二维离散时间系统作为一个典型的例子,已经成为一个重要的研究课题,引起了广泛关注。到目前为止,已经提出了几种不同的二维状态空间模型。其中Fornasini-Marchesini II(F-M II)模型被认为是最普遍的模型,它涵盖了其他模型的特殊情况。且F-M II 模型也已经取得了丰硕的成果,特别是在稳定性和可观性、滤波和估计以及控制器设计等问题上[3]。

多维系统的另一个重要研究方向是实现问题,即通过确定的多维状态空间模型来实现给定的有理传递函数或状态矩阵[4]。与一维系统不同,通常n维(n≥2)系统的最小状态空间实现很难获得。为了分析多维系统,就必须解决实现问题,最常用的解决方法是使用规范形式获得低阶实现矩阵。但基于规范形式的方法大多只能给出系统的一种可能实现,通常情况下系统有很多解[5]。与规范形式不同,图论方法可以直接从特定结构中获得系统的一组最小状态空间实现。比如,文献[6]的图论方法用一系列的二项式有向图构造系统的实现矩阵,但这种方法不适用于多维多输入多输出(multiple-input multiple-output,MIMO)系统,且目前没有在F-M II模型中使用。

本文结合多维图论和F-M II 状态空间模型之间的联系,提出了一种二维多输入多输出F-M II 模型实现矩阵求解的新方法,该方法将文献[6]的一维实现方法扩展到二维系统,然后提出了多维MIMO 系统的实现方法。该算法与规范形式实现方法相比,实现过程更加清晰直观,获得实现矩阵数量更多,且状态矩阵形式便于计算机分析,为高速计算分析多维系统提供了新思路。

1 F-M Ⅱ状态空间模型

二维线性系统的F-M II 状态空间模型[7]为

其中,x(i1,i2)∈Rr、u(i1,i2)∈Rl和y(i1,i2)∈Rm分别是局部状态量、输入量和输出量;A、B、C、D为实数矩阵;A1、A2∈Rr×r、B1、B2∈Rr×l、C∈Rm×r、r被称作二维F-M II 模型的阶数。通过系统模型的化简,也能使用(A,B,C,D)表示,其中A≜(A1,A2) 和B≜(B1,B2) 表示二维系统。

二维离散系统的传递函数被表示为

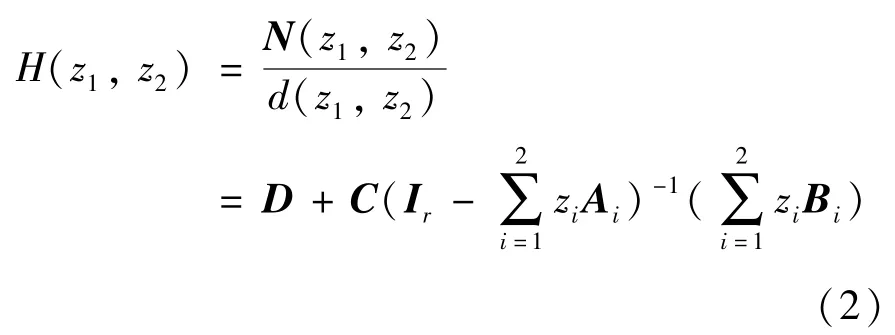
其中,N(z1,z2) 表示传递矩阵,d(z1,z2) 表示特征多项式,zi表示延迟操作[8]。

对于给定的二维传递函数H(z1,z2),如果存在矩阵A、B、C、D使得式(2)成立,则称其为F-M II 模型的实现矩阵。如果系统的传递函数H(z1,z2) 中N(z1,z2) 和d(z1,z2) 都是二维多项式,当d(0,0)≠0 时,称这个系统是因果系统。当d(0,0)≠0 且n(0,0)=0 时,称系统是严格因果系统。在不失一般性的情况下,可以假设传递函数是严格因果系统,D=H(0,0) 为零阶矩阵,将最小化问题归结为求实数矩阵的问题。如果H(z1,z2) 是因果传递函数但不是严格因果传递函数,只需要重新定义H(z1,z2)为H(z1,z2)-H(0,0),则能得到H(z1,z2) 为严格因果传递函数[9]。

2 设计实现

传递函数H(z1,z2) 中的D为常数矩阵,在不失一般性的情况下,考虑式(2)中D为零阶矩阵的传递函数,表示为分式结构如下。

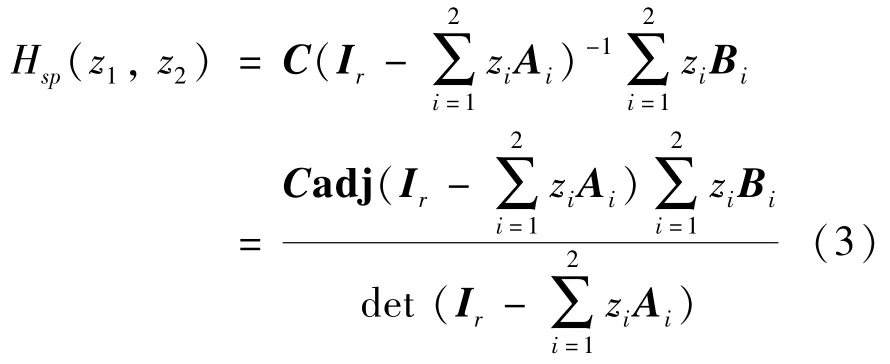
本文考虑F-M II 模型为一种多输入多输出(MIMO)状态空间模型。则式(3)中的传递函数可以表示为

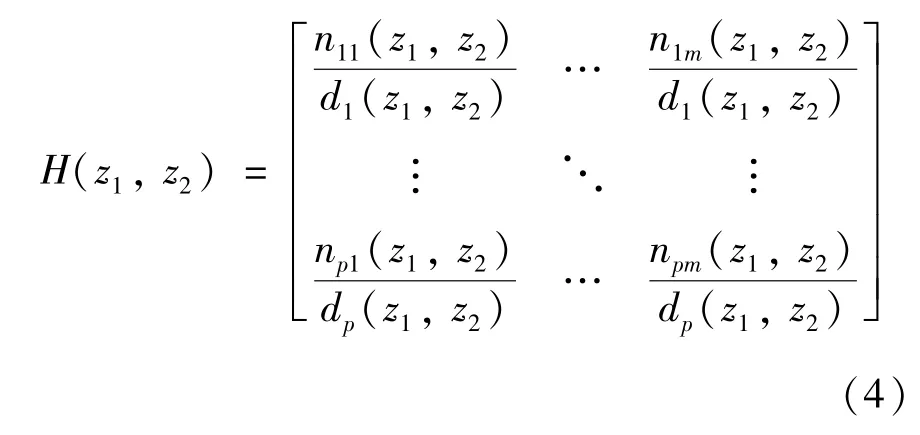
由式(4)可知,dj(z1,z2) 和nij(z1,z2) 可以写成如下形式:

从式(2)中可以获得实数矩阵D。

由式(3)可以确定以下形式的严格因果传递函数:

为确定二维离散系统的实现矩阵,将传递函数的分子和分母乘以,得到:

其中,

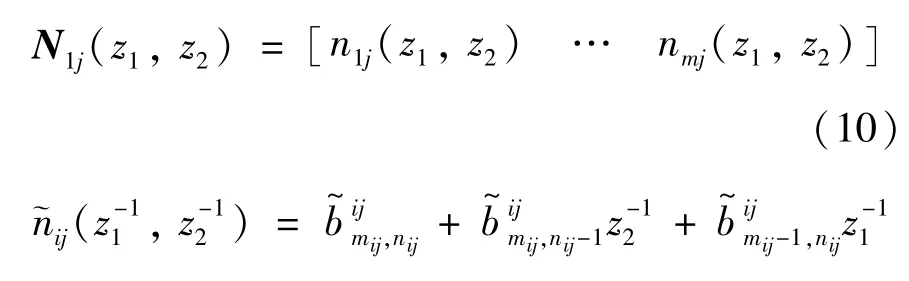
特征多项式例如在一维系统中一个域F ∈R,对分布于F 上的n × n矩阵A,其特征多项式定义由式(12)给出。对于二维离散系统,特征多项式由两个变量z1和z2组成。对于式(3)描述的离散时间系统,特征多项式如式(13)所示。

有向图理论一个有向图D是由非空有限集V(D)和A(D)构成。其中V(D)和A(D)分别为有向图D的顶点集和弧集,顶点集V(D) 中每一个元素为有向图D的顶点,A(D) 中每一个元素为有向图D的弧。有向图常被简记为D=(V,A),其中V和A分别表示有向图D的顶点集和弧集。有向图D的阶是D顶点的数目,D的阶可以被直接写作| D|;有向图D的大小是D中弧的数目。二维有向图D2由6 个元素组(S,V,N1,N2,B1,B2) 组成,其中S为源,V={v1,v2,…,vn} 为顶点的集合,N1、N2为V×V的子集,其元素分别被称为N1弧、N2弧,同时B1、B2是S×V的子集,其元素分别被称为B1弧、B2弧[10-11]。如果传递函数H(z1,z2)中的A1和A2不是零阶矩阵,则存在有从顶点Vi到顶点Vj的N1、N2弧集。如果输入矩阵B不是零阶矩阵,则存在从源S到Vi的B1、B2弧集。可以用实线来表示N1和B1弧,虚线表示N2和B2弧。

交集顶点交集顶点是由文献[12]中给定的特征多项式组成的所有二项式有向图的交集的顶点。由于问题的复杂性,在本文中讨论的是这样一种情况,即所有二项式有向图的起点和终点都相交于同一交集顶点的情况。

引理如果满足以下条件[13]:

(1) 特征多项式传递函数H(z1,z2) 的d(z1,z2) 满足:di,j≥0(i=0,1…,k1;j=0,1,…,k2;=1)。

(2) 特征多项式传递函数的有向图中循环的个数等于该多项式中每个单项式有向图的个数相加总和。

(3) 特征多项式传递函数的有向图中所有循环的起点和终点都相交于同一个顶点,则能求出特征多项式传递函数H(z1,z2) 的实数矩阵A、B、C、D。

证明引理中(1)当且仅当考虑特征多项式为正时必须满足,否则必须满足(2)和(3)。引理中(2)如果特征多项式传递函数的有向图中循环的个数多于该多项式中每个单项式有向图的个数相加总和,则会有额外的单项式形成,最终计算得到的特征多项式与原特征多项式不同。引理中(3)即有向图满足则有向图属于K1类有向图[14]。如果存在两个循环的起点和终点不相交于同一顶点,则多项式有向图解会出现B和C矩阵并发症,需要追踪源到输出的所有路径。文献[15]给出了具体的证明过程。

3 算法步骤

本文提出的新方法首先为所有构成特征多项式的二项式创建有向图,然后利用顶点的相对组合将它们连接起来,创建特征多项式可能的有向图变体,最终实现给定的特征多项式。算法的各个部分都可以并行,这对于快速开发计算机算法具有重要的意义。算法将文献[6]中的一维实现方法扩展到二维,且在原有的基础上增加了有向图的组合规则,有利于从二维有向图中获取B和C矩阵。

算法确定实现矩阵

(1)把特征多项式d(z1,z2) 分解成多个单项式。

(2)根据有向图方法,画出每个单项式的有向图。

(3)基于每个单项式各自的有向图,确定特征多项式有向图。

(4)特征多项式有向图循环个数等于单项式有向图个数之和且所有循环的起点和终点都相交于一点。

(5)通过特征多项式有向图的弧集确定对应的状态矩阵Aij。

(6)对交集顶点,创建从源到输出的所有路径。

(7)添加所有路径的单项式,然后创建多项式。

(8)分配属于B的单项式,形成一组方程,根据方程求解B和C矩阵。

算法由3 部分组成,第1 部分为步骤(1)～(2),将特征多项式表示为每个单项构造的有向图;第2部分为步骤(3)～(5),使用单项式有向图表示有效的多项式结构;第3 部分为步骤(6)～(8),通过在特定的结构中添加两种类型的顶点,允许直接从二维MIMO 系统有向图中获得B和C矩阵。

本文算法的优点是引入源顶点和输出顶点,不需要借助Matlab 工具箱计算B和C矩阵。矩阵B和C可通过添加2 个额外类型有向图的顶点输入顶点S和输出顶点Y直接获得。顶点V和S之间的弧值对应输入矩阵B,顶点V和Y之间的弧值对应输出矩阵C。在二维单输入单输出(single-input single-output,SISO)系统中引入本算法的两种顶点。例如,对于一个SISO 传递函数:

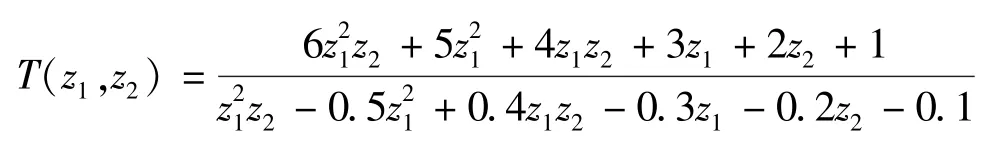
计算适当的实现矩阵D:

将传递函数T(z1,z2) 乘以,由式(9)和式(11)可以得到:

组合图1 单项式有向图表示特征多项式,选择符合引理的一个有向图,组合结构如图2 所示。

图1 实现单项式M1、M2、M3、M4、M5 有向图

根据图2 有向图D的弧集得到对应F-MII模型的矩阵Ai。

图2 有向图D 实现特征多项式d(z1, z2)

然后添加两种节点可得到结构如图3 所示。

图3 有向图实现特征多项式n(, )

根据图3 中有向图的弧集得到对应F-M II 模型的矩阵Bi和C。

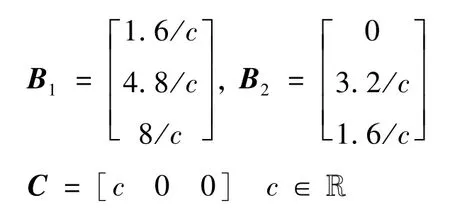
因此能通过添加两种类型节点得到二维F-M II模型的矩阵B和C,且该实现矩阵为一组最小实现。在一维算法中提到了多输入单输出(multiple-input single-output,MISO)的情况,本文将在MIMO 情况中讨论二维MISO 的情况。

4 数例

考虑如下(MIMO)二维系统的传递函数:

将矩阵分块得到2 个MISO 传递矩阵:

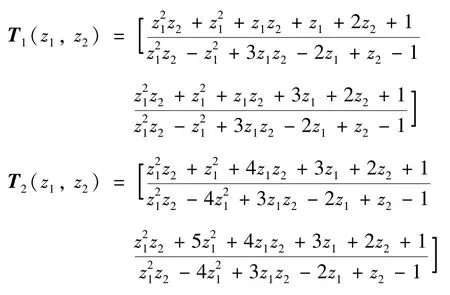
先对于T1(z1,z2) 进行求解:

步骤1确定矩阵D。

由式(4)～式(11)可以得到以下等式:

将d(z1,z2) 乘以,并且写成二项和的形式,结果如下:

其中∪是对有顶点的有向图操作,称为相对于顶点的复合[16]。对于每个单项式,创建满足引理的图结构,选择其中一个进行研究。所选结构如图4 所示。

图4 有向图D 实现特征多项式d(z1, z2)

步骤2确定状态矩阵A。

从获得的有向图中可以对应获得状态矩阵A1和A2。

步骤3确定矩阵B和C。

将N(z1,z2) 乘以z-21z-12,可以获得新的有向图多项式:

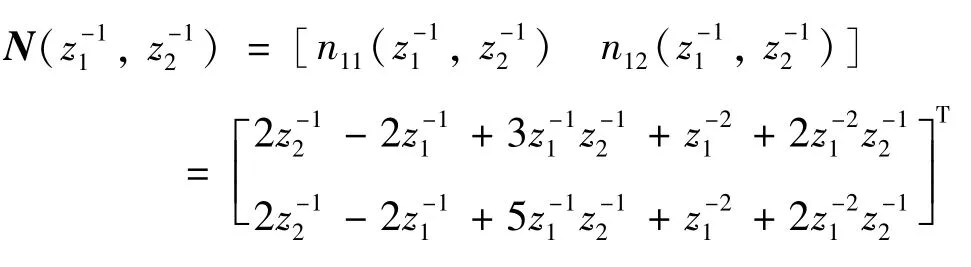
对图4 的有向图添加源节点S和输出节点Y,并且连接起来。在本文的数例中,源节点与图4 中的公共顶点相连。假设矩阵C包含一个非零项,则可得到2 个部分。

图5 有向图实现特征多项式n11(,)

整理上式写成如下形式:

图6 有向图实现特征多项式n12(,)

值得注意的是,两个部分的输出矩阵C具有相同的结构,而输入矩阵B依赖弧w(v1,y1)的值。因为系统分为两个部分,所以输入矩阵B1和B2可以表示为如下形式:

输出矩阵C则表示为

现在对T2(z1,z2) 进行求解,重复上面的步骤,经过计算可得:

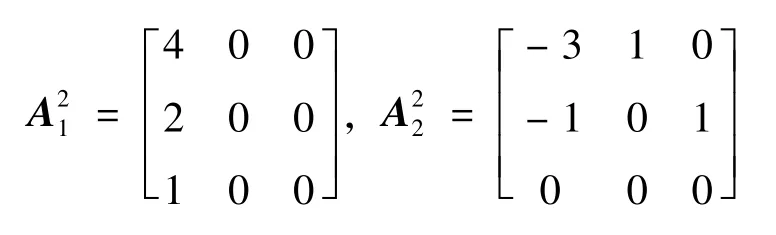
则二维MIMO 系统F-M II 模型实现为

对于同一类型的特征多项式,可以有图2 和图4 两种有向图结构。用同样的方法还可以创建满足引理的其他有向图结构。将本文方法与其他标准形式求解算法[17-20]获得实现矩阵的大小和数量进行详细对比,结果如表1 所示。充分说明了本文方法在获取求解数量和实现矩阵阶次方面的优越性。该算法能够为特征多项式创建一组完整的解,但解的数量随着特征多项的幂和系统维度的增长而呈指数增长。用Matlab 进行仿真,结果如图7 所示。

图7 算法获得特征多项式实现矩阵的数量

表1 比较实现矩阵阶次和实现数量

5 结论

本文提出了基于F-M II 状态空间模型的多维系统图论实现的新方法,通过在特征多项式结构中引入源顶点和输出顶点,该方法能够从多维系统的传递矩阵中获取F-M II 状态空间模型的一组A、B、C、D矩阵。不同于经典的规范方法只有一种实现,本文方法在获得完整实现的同时可以调整交集顶点的位置得到多种实现,并给出了具体的数例验证新方法的有效性和可行性,为多维系统的研究提供了新思路。将此算法应用在MIMO 系统中,可以获得更低阶次且数量更多的实现矩阵,简化了MIMO 系统实现矩阵求解的难度。今后更进一步的研究是减少特征多项式结构的限制,并尽可能减少算法的步骤和复杂度,使之能够在计算机中求解多维系统的实现矩阵。