基于POI 的出租车停靠位置选择算法研究①
2021-02-11徐焕君张玉停
徐焕君 余 靖 苑 帅 张玉停
(燕山大学信息科学与工程学院 秦皇岛066004)
0 引言
随着互联网技术的快速发展,传统出租车行业面临着网约车的竞争,其中一个重要原因就是出租车等待位置以及资源分配不合理而造成的打车难问题。如何合理选择出租车停靠位置属于城市交通设施建设的一个主要问题,也是城市规划[1]的重要依据。
城市兴趣点(point of interest,POI)数据涵盖了广泛的地理空间位置属性,相关学者使用POI 为评价城市布局合理性提供了新的研究方法。文献[2]基于地理信息系统(geographic information system,GIS)和POI 数据,研究了上海市的城市中心体系,与上海市现行城市总体规划进行对比,并提出发展建议。文献[3]基于POI 数据对苏南4 个城市的生活便利度进行评价,为公共服务设施空间分布及其便利度评价提供了新的方法。文献[4]基于住宅POI 数据,考虑城市公园绿地对周边住宅价格的影响,构建了住宅市场特征价格模型并结合弹性与边际价格分析,量化了公园绿地对住宅价格的影响。
基于POI 的出租车停靠位置是根据节点重要度来选择的,用于判定网络节点重要度的方法本质上源于图论[5]。目前的研究均是仅以一种类型的场所作为研究对象,如公交站点、地铁站点、铁路站点等,而没有综合考虑多类型场所。判定重要节点的方法除了度数法[6]和介数法[7]之外,考虑到整个网络的全局特性,又将贴近度中心性[8]、介数中心性[9]等也作为评价指标加入算法中。文献[10]提出一种基于熵的复杂网络节点重要性自适应判定方法,但采用的判定指标有一定的局限性。文献[11]提出了一种基于生成树数目的节点删除法,但节点删除可能会造成网络不连通,从而使判定结果不准确。文献[12]提出一种基于全网平均等效最短路径数的网络抗毁度评价模型,但没有完全体现出网络拓扑结构的差异性。网页排名(PageRank)算法[13-14]不仅可以预测网络流量、未来链路等,还可以识别重要节点,且其计算复杂度较低。此外,文献[15,16]提出了融合节点自身重要度及连边重要度的改进加权节点收缩法,主要用于判定供应链网络节点间的重要度。文献[17]利用A*算法,将复杂网络理论与动态需求特征相结合,对公交站点进行重要度判定,解决了定制公交站点及路径动态优化问题。文献[13-17]主要是针对单一类型节点判定重要度,具有一定的局限性。
本文在综合考虑节点在路网[18]中基本信息的前提下,建立了一种在不同模式下出租车按需分配呼叫模型,给出适用于无权节点和加权节点的重要度判定方法,并以POI 数据集为参考,对节点重要度进行排名,根据排名结果,依照杠杆原理和多边形求“重心”方法,找出最适合的出租车停靠位置,并实现可视化。
1 系统模型
本节首先从城市道路网络的结构特性出发,基于选取的POI 处产生的呼叫出租车次数的不同提出4 种模式。将城市中对于出租车需求量大的场所抽象为网络中的节点,将不同POI 之间的运行线路抽象为节点间的连接边,基于此得到城市道路拓扑网络是一个复杂网络。该网络形成的拓扑图是一个无向图,数学表达式为G=(V,E) 是一个有序的二元组。其中V=(v1,v2,…,vm) 称为点集,其元素称为顶点或节点;E=(e1,e2,…,en) 称为边集,其元素称为无向边,简称边。
图G的邻接矩阵A=[aij],其中,

1.1 呼叫模型
1.1.1 加权节点的权
(1)节点类型共有8 种,分别为车站a、住宅区b、学校(高校)c、医院d、景区e、酒店f、餐馆g 和购物广场h。
(2)时间参数共有4 种,分别为早上mor、中午noon、下午aft 和晚上eve。
1.1.2 4 种出租车呼叫模式
模式1totalSame。不同节点处产生出租车呼叫次数相同,呼叫次数是一个有范围的随机数,随机数的产生受时间参数控制。
模式2typeSame。相同类型的节点产生出租车呼叫次数相同,不同类型的节点之间产生的呼叫次数不考虑是否会相同。呼叫次数是一个有范围的随机数,随机数的产生受时间参数控制。
模式3random。不同节点处产生出租车呼叫次数是随机的,随机数的产生受时间参数控制。
TotalSame、typeSame、random 模式随机数选择方案如表1 所示。

表1 totalSame、typeSame、random 模式随机数选择方案
模式4human。人工干涉节点处出租车呼叫次数,指定被选择节点处的呼叫次数为一个较大的随机数,其他节点处的呼叫次数的产生方式与total-Same 模式一致。
Human 模式随机数选择方案如表2 所示。
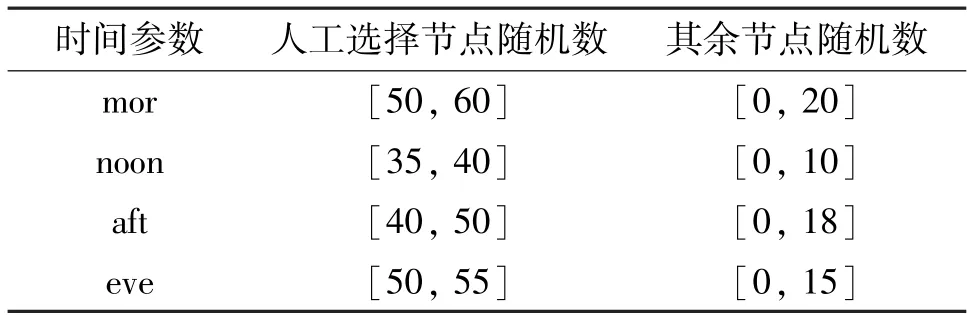
表2 human 模式随机数选择方案
1.2 相关定义
定义1 节点邻域(neighborhood)与闭邻域(closed neighborhood)。设无向图G=<V,E >,vi,vj∈V,若∃et∈E,使得et=(vi,vj),则称vi与vj是相邻的,即aij=1。节点vi邻域为δi={vj | vj∈V,aij=1,j=1,2,…,n}。节点vi闭邻域为={vi} ∪δi。
1.2.1 节点加权系数
本文中节点的权值为节点处出租车的随机呼叫次数,该指标的提出是考虑到判定节点重要度时除了拓扑图本身结构属性之外,还受到POI 即节点处权值大小的影响。在其他条件相同的前提下,节点处的权值越大,节点越重要,说明该指标的贡献度越高。根据各POI 处对出租车的随机呼叫次数,提出节点加权系数为不同节点处的出租车呼叫权重,也称为节点贡献度。
定义2局部加权系数(local weighting factor,LWF)。节点的局部加权系数为节点闭邻域中的权值和,节点vi处的出租车呼叫次数为,节点vi邻域的出租车呼叫次数为,则节点vi的局部加权系数可以定义为

为了简化计算,缩小量值,将上述局部加权系数的值进行归一化,使结果范围在[0,1]之间。使用的归一化方法如式(2)所示。

定义3全局加权系数(global weighting factor,GWF)。节点的全局加权系数为节点vi处的权值与整个网络图中所有节点的权值和之比,节点vi的全局加权系数为

1.2.2 局部重要度
定义4节点的度(degree)及其闭邻域的度(degree of closed neighborhood,CND)。节点vi的度等于和vi相关联的边的条数,又称关联度,记作dG(vi)。节点vi闭邻域的度为

式中,dG(δi) 为节点vi的邻域集合中所有节点的度的累加和。
Sigmoid 函数也叫Logistic 函数,在信息科学中,由于其单增以及反函数单增等性质,Sigmoid 函数常被用作神经网络的激活函数,将变量映射到0~1 之间。

为了将节点闭邻域的度的值映射到0~1 之间,对原Sigmoid 函数进行一个变形。

其中x的取值范围为[0,+∞),s(x) 的取值范围为(0,1)。
定义5节点邻域度密度(neighborhood degree density,NDD)。将节点vi邻域集合中节点的度数之和与节点vi的度的比值定义为节点vi的邻域度密度,代表着节点的邻域关系。节点vi的邻域度密度为

定义6基于度的点密度(dot density,DOTD)考虑了节点闭邻域的度与节点邻域集合的度密度之间的关系,其定义如式(8)所示。

定义7节点的局部集聚系数(agglomeration coefficient,AGGC)。节点vi的邻居节点之间所存在的边数与可能存在的最大边数之比。节点vi的局部集聚系数为

该指标考虑了节点的邻居节点之间的紧密程度。
1.2.3 全局重要度
定义8接近中心性(proximity centrality)。假设图中共有m个节点,是节点vi到节点vj的距离(按经纬度计算),di是节点vi到网络中所有节点的距离的平均值。节点vi的经纬度为节点vj的经纬度为,则两点经纬度间的距离公式为

式中r为地球平均半径,通常选择常数值为6371 km。
节点vi的全局重要度(global importance)为
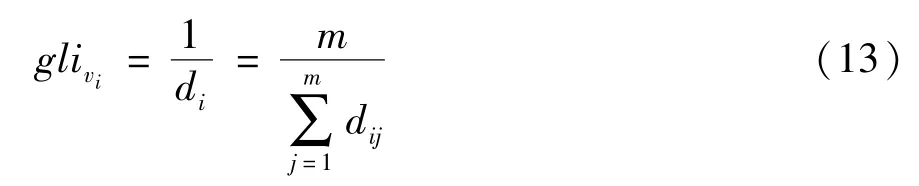
其中,di值的相对大小在某种程度上反映了节点vi在网络中的相对重要性,di的值越小意味着节点vi更接近其他节点,越居于网络中心,节点vi在全局网络中越重要。
1.2.4 节点重要度
复杂网络本质上的非同质拓扑结构,决定了网络中每个节点的重要程度是不同的。节点在复杂网络中的重要度首先取决于节点在网络中的位置,如网络中的“末梢节点”和“非末梢节点”的重要程度显然是不一样的;其次,节点在网络中的重要度还取决于节点的连通能力,该节点连接的边数越多,节点就越重要;除此之外,本文中提出的节点处的权值大小也影响着节点的重要程度。
定义9通用节点重要度(general node importance degree,GNID),称

为节点vi是通用节点时的重要度。通用节点在本文里特指无权节点,即节点处无权值。
定义10专用节点重要度(dedicated node importance degree,DNID),称

为节点vi是专用节点时的重要度。专用节点在本文里特指加权节点,即节点处有权值。
2 算法描述
复杂网络中节点的重要度由节点在复杂网络中的位置和在其邻域中的度以及节点处的权值大小共同决定。
2.1 GNI 算法
本文通用节点重要度(general node importance,GNI)计算方法可以在常见的网络图中使用,节点处无权值,它考虑的是节点在网络中的基本结构,综合节点在局部区域和全局中的信息,设计算法过程如算法1 所示。

2.2 DNI 算法
本文专用节点重要度(dedicated node importance,DNI)计算方法是在DNI 算法的基础上设计的,它除了综合考虑节点在网络中的基本结构信息外,还增加了节点加权系数(贡献度)这一指标,更适用于本文的研究背景,算法过程如算法2 所示。


GNI 算法适用于节点处无权值的情况下求节点重要度。DNI 算法适用于节点处有权值的情况下求节点重要度。DNI 算法更适用于本文的研究背景,在POI 处对出租车有需求,即在节点处有权值的情况下判定节点重要度。
2.3 出租车停靠位置选择算法
出租车停靠位置的选择依据周围节点的重要程度,在多个重要程度不同的节点之间的某个位置选择出租车停靠点时,需要考虑到停靠位置到节点的距离及节点的重要程度两个因素。本文类比多边形获取“重心”的方法,求得最佳的出租车停靠位置。
已知节点vi,其在平面坐标系中的坐标为(,),米勒坐标系中的坐标为。米勒坐标系下坐标转化至平面坐标系下坐标公式为

得:

在平面直角坐标系下:

已知点o(xo,yo),其在平面坐标系中的坐标为(xo,yo),在米勒坐标系中的坐标为。平面坐标系下坐标转化至米勒坐标系下坐标公式为


式中mill=2.3,最终结果留到小数点后7 位。出租车停靠位置选择算法过程如算法3 所示。

3 实验结果分析
3.1 数据集
本文选取的POI 为河北省秦皇岛市北戴河区113 家对出租车有较大需求的8 类场所,分别为车站、住宅区、学校(高校)、医院、景区、酒店、餐馆和购物广场,如图1 和图2 所示。这113 家场所的选取来自当前热门APP 推荐并且根据真实的经纬度数据(北京大学开放数据平台和高德地理信息集)与高德地图实际行驶路线构成城市道路网。城市道路网是在城镇管辖范围内由节点和各种不同功能的干道和区域性道路组成的,是城市总体规划布局的骨架。

图1 POI 及出租车可行驶路线网络图

图2 POI 按类型显示及出租车可行驶路线网络图
选取北戴河区的POI 作为研究数据的原因:(1)北戴河区交通基础设施建设还在发展中,没有市中心发达,公交站点密度也比较小;(2)因为旅游等需求,人口流动量大;(3)堵车情况不严重,出租车市场发展潜力大。
3.2 实验
为求得北戴河区最佳的出租车停靠位置,共进行2 组实验。第1 组实验根据定义8 和定义9 分别在4 种模式下以GNI 算法和DNI 算法求出图中113个节点的重要度排名,通过比较两种算法下的排名可以看到,在节点处有权值时会影响节点的重要度。第2 组实验根据DNI 算法下的节点重要度排名,选出排名前5%的节点,依据出租车停靠位置选择算法,求得最佳的出租车停靠位置。
下面的各个实验是对于不同模式下DNI 算法与GNI 算法节点重要度变化量排名前5 结果对比。
3.2.1 节点重要度排名
(1) totalSame 模式
如图3 所示,由实验结果可知,当考虑节点处的权值时,会对最终节点重要度的排名结果产生明显的影响,排名结果与权值大小无关。并且,若所有POI 处的呼叫次数为0 时,即节点处的权值大小为0时,DNI 算法的节点重要度排名与GNI 算法下的排名一致。
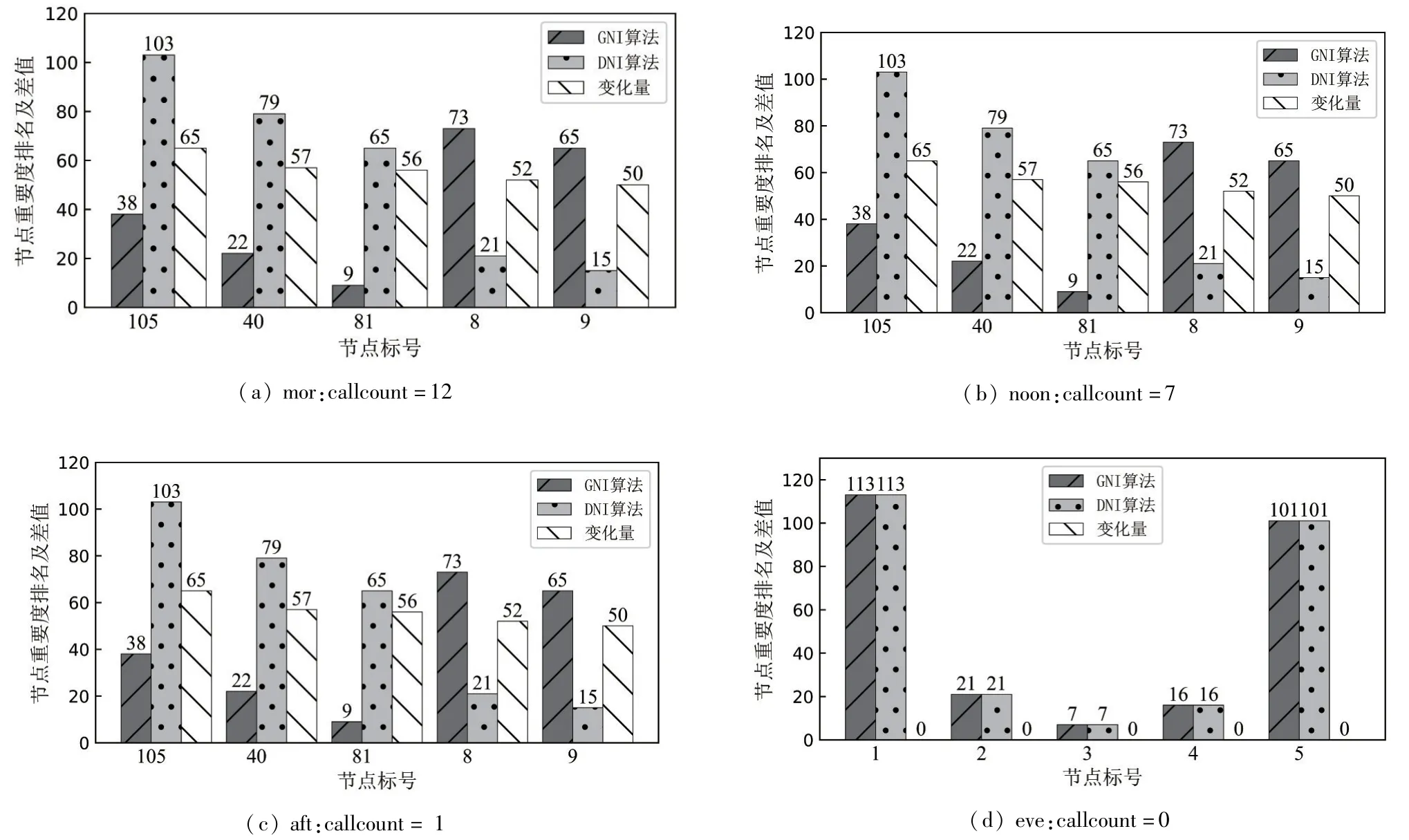
图3 totalSame 模式
(2) typeSame 模式
如图4 所示,该模式下,相同类型的节点处产生的呼叫次数相同。时间参数为mor 时,8 种类型节点的呼叫次数分别为5、3、7、7、0、4、1、0;时间参数为noon 时,8 种类型节点的呼叫次数分别为9、0、5、0、2、3、1、6;时间参数为aft时,8种类型节点的呼叫次数分别为6、9、16、7、15、9、4、5;时间参数为eve时,8 种类型节点的呼叫次数分别为12、3、2、6、1、4、5、1。由实验结果可知,typeSame 模式下,节点重要度排名在DNI 算法下与GNI 算法下有明显变化。


图4 typeSame 模式
(3) random 模式
如图5所示,该模式下,不同节点处产生的呼叫次数是在时间参数的控制下随机生成的。由实验结果可知,random 模式下,节点重要度排名结果在DNI 算法下与GNI 算法下有明显变化。

图5 random 模式
(4) human 模式
如图6 所示,该模式下,人工选择标号为50 的节点,此节点处产生一个较大的随机数,而其余节点产生的随机数方式与totalSame 模式一致。时间参数为mor 时,{50 号节点:58,其他节点:14};时间参数为noon 时,{50 号节点:37,其他节点:0};时间参数为aft 时,{50 号节点:45,其他节点:2};时间参数为eve 时,{50 号节点:50;其他节点:5}。

图6 human 模式
由实验结果可知,human 模式下,节点重要度排名在DNI 算法下与GNI 算法下有明显变化。
3.2.2 出租车停靠位置选择
本文节点重要度排名方法选取DNI 算法,以human 模式下,设定时间参数等于mor 时为例,生成出租车停靠位置并将其结果可视化。
根据出租车停靠位置选择算法,排名前5%的节点的出租车停靠位置如图7 所示(黑色粗加号)。从表3 及图7 中可知,排名第2 的节点与排名第4的节点分别在其闭邻域中找最合适的出租车停靠位置时,得到的结果一致。因为标号为56 的节点与标号为70 的节点互为闭邻域的关系,在通过出租车停靠位置选择算法计算时,是会出现结果一致的可能性的。而在该模式下,标号为50 的节点处随机数为56,此时节点加权系数对50 号节点的重要度排名及最终的出租车停靠位置都有影响。
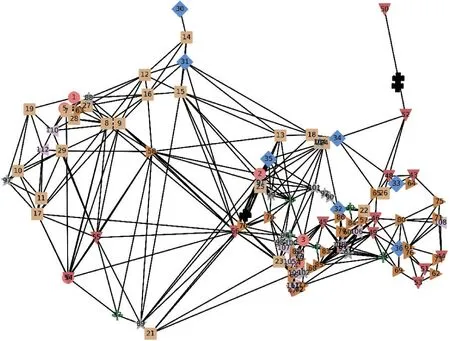
图7 出租车停靠位置在网络图中的可视化

表3 human 模式下(时间参数为mor)出租车停靠位置选择方案
本文以北戴河区113 个POI 进行实例分析,得出以下结论。
(1) POI 处的呼叫次数大小,即节点处随机数的权值大小,会影响节点重要度的排名结果。
(2) 节点的权值与节点在图中的基本属性之间并无相关性,进一步说明单个指标具有不同侧重点,而综合指标更能从物理拓扑结构及呼叫次数属性方面体现节点的重要性。
(3) 出租车停靠位置的选取与POI 处的重要性相关,停靠位置会更靠近较为重要的POI。
4 结论
本文选取北戴河区113 个POI,考虑了其实际地理位置信息与出租车行驶路线,提出了POI 处出租车呼叫的次数作为新指标,建立了一种具有不同模式的出租车按需分配呼叫模型。该模型更适合于判定加权节点的重要度,同时基于节点的重要度排名,给出了较好的出租车停靠位置。下一步的研究方向会将出租车的实际行驶距离以及行驶道路上需要经过的红绿灯数等指标考虑进去,以得到更好的出租车停靠位置。
