深度思考之三角函数——数学文化中的三角问题

王思俭

中国古代数学的成果辉煌，涌现一大批数学家，他们留下了许多名著，如《海岛算经》《九章算术》等，许多成果在当时都处于世界领先水平．继承和发扬我国古代数学文化是十分必要的，弘扬古代科学家精神是永恒的文化自信．下面，一起来看看我班同学在一堂数学文化课上的表现吧．

真题再现1（2021·全国乙卷理科第9 题）魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作，其中第一题是测量海岛的高，如图，点E，H，G在水平线AC上，DE和FG是两个垂直于水平面且等高的测量标杆，其高度称为“表高”，EG长称为“表距”，GC和EH的长都称为“表目距”，GC与EH的长度差称为“表目距的差”，则海岛的高AB=（ ）

勤奋的小A：我尝试了一下，一直在简单的三角形相似里绕圈，始终绕不出来．

“长手哥”支一招：读懂题意是第一位的．多读几遍题，理解题目中各个名词的含义，并对照图形标出这些名词，如“表高”是哪条线段？“表目距”是哪条线段？再研究这些线段在哪几个直角三角形中，最后解直角三角形．

收纳袋

数学文化题中往往会出现一些新名词，理解其含义是首要的；其次，我国古代数学比较注重应用性，本题为测量海岛的高，“如何测量”是接下来要理解的．

恍然的小A：表面上是关于线段长度的题，但如果脱离角度，很难得到结果，所以我尝试设角度．

设∠AHB=α，∠ACB=β，由已知条件得DE=FG．

在Rt△DEH中，；在Rt△FGC中，

因此，在Rt△ABH中，

在Rt△ABC中，

代入AB的计算式子，得又怎么转化呢？

机灵的小B：想办法消去HC，同时要凑出分母CG-EH．

因为HC=HG+CG=EG-EH+CG，代入AB的算式，

又因为DE是表高，所以选A．

机智的小C：我有妙招！根据等高且垂直AC，这样可以构成矩形，同时选项中有“表高”，所以就想到连接FD．

收纳袋

你发现测量高度问题一般要用到正切的原因了吗？

要测量的高度为直角三角形的一条直角边，而能简单测出来作为已知条件的则有仰角以及位于地面的另一条直角边长，正切便呼之欲出了！

连接FD并延长，交AB于M，则AB=AM+MB．

又DF∥AC，所以∠BDM=∠BHA=α，∠BFM=∠BCA=β，

“长手哥”有话说:解法一在两组相似三角形中分别表示出AB的长，思路自然，解法二简单明了，运算速度较快．两种解法都体现了“算两次”的数学思想，且都跟正切联系紧密．“算两次”也是测量问题中常用的重要方法．

真题再现2（2021·全国甲卷第8 题）2020年12月8日，中国和尼泊尔联合公布珠穆朗玛峰最新高度为8848．86（单位：m），三角高程测量法是珠穆朗玛峰测量法之一，右图是三角高程测量法的一个示意图，现有A，B，C三点，且A，B，C在同一水平面上的投影A′′C′,,满足∠A′C′B′=45°，∠A′B′C′=60°，由C点测得B点的仰角为15°，BB′与CC′的差为100，由B点测得A点的仰角为45°，则A，C两点到水平面A′B′C′的高度差AA′-CC′约为（）（ ）

A．346 B．373 C．446 D．473

踊跃的小A：作CD⊥BB′于D，则BD=100，由C点测得B点的仰角为15°，所以由平面几何知识得

敲黑板

你“get”到“三角高程测量法”这个名字的点了吗？

上一题是在一个垂直于地面的平面上进行测算，而此题测量法相当于将原平面进行了折叠，且A，B，C都不在地面上，这也为测量非常高的山峰，提供了合理的前期数据．（如CC′也可以同样由更低的高度来测算得到）

在△A′B C′′中，由正弦定理得

但怎样利用由B点测得A点的仰角为45°求AA′CC′-？

机智的小B：过点B作BE⊥AA′于E，因 此∠ABE=45°，△ABE为等腰直角三角形，所以AE=BE．又可以证明四边形A′B′BE为矩形，所以

过C作CF⊥AA′于F，于是AA′-CC′=AF，再利用正弦定理求出

但C点测得A点的仰角不知道，又如何求AF呢？

“长手哥”支一招：你已经求出再观察图形几何特征，想办法求EF．

恍然的小B：连接DF，因为C′C∥B′D，C′C∥A′F，且C′C=B′D，C′C=A′F，所以四边形A′B′DF为平行四边形，且为矩形，因此DF∥B A′′，且DF=B A′′，所以DF∥BE，且DF=BE，所以四边形BEFD为平行四边形，也为矩形，于是有EF=BD=100．

“长手哥”做总结：解三角形文化背景的实际问题四部曲：

1.首先阅读理解题意，从字里行间和几何图形中，分清已知条件是什么，要求的目标是什么．

2.其次确定求解策略，从已知目标到待求目标应该怎么走？有哪些可用的求解工具（正弦定理、余弦定理、面积公式等）？还缺少什么条件？又怎样创造条件（如设相关未知量、整体代换等）？是否有隐含条件没有找到（如锐角三角形）？

3.再其次建立数学模型（如三角函数、直角三角形中正切函数等），再运用数学知识求解（如函数与方程思想、数形结合、换元法等）．

4.最后回到实际问题作答.

实战演练

1.（2020·北京卷）2020年3月14日是全球首个国际圆周率日（π Day）．历史上，求圆周率π 的方法有多种，与中国传统数学中的“割圆术”相似．数学家阿尔·卡西的方法是：当正整数n充分大时，计算单位圆的内接正6n边形的周长和外切正6n边形（各边均与圆相切的正6n边形）的周长，将它们的算术平均数作为2π 的近似值．按照阿尔·卡西的方法，π 的近似值的表达式是（ ）

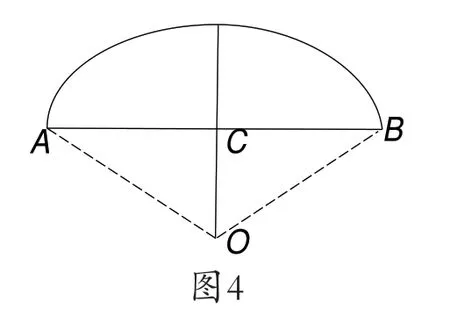
2.《九章算术》是我国古代数学成就的杰出代表．其中《方田》章给出计算弧田面积所用的经验公式为：弧田面积=(弦×矢+矢2)．弧田（如图），由圆弧和其所对的弦所围成，公式中的“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差．按照上述经验公式计算所得弧田面积与其实际面积存在误差．现有圆心角，弦长等于9 m 的弧田．

（1）计算弧田的实际面积；

（2）按照《九章算术》中弧田面积的经验公式计算所得的结果与（1）中计算的弧田实际面积相差多少？（结果保留两位小数）