直观引领 理性分析——一道立体几何多选题的探究过程

王盈慧

有这样一道立体几何多选题引起了我班同学的热烈讨论．

问题（多选题）如图1，菱形ABCD中，AB=2，∠DAB=60°，E是AB的中点，将△ADE沿直线DE翻折至△A1DE的位置后，连接A1C，A1B，若F是A1C的中点，则在翻折过程中，下列说法正确的有（ ）

图1

A．异面直线A1E与DC所成的角不断变大

B．二面角A1-DC-E的大小最大为30°

C．点F到平面A1EB的距离恒为

D．当A1在平面EBCD的投影为E点时，直线AC1与平面EBCD所成角最大

一、直观体验引路

剪一个如题中所述菱形，按题意翻折，观察点A的运动变化规律，并观察点F随之如何运动变化，直观感知二面角A1-DC-E、直线A1C与平面EBCD所成角的变化．

变化1：如图2，显然，A1E扫过的区域是个半圆面，且与底面垂直，直线A1E与BE所成的角先变大，到后再变小；

图2

变化2：对于二面角A1-DC-E，直观感知点A1位于距平面EBCD最远处时其二面角最大，直线AC1与平面EBCD所成角也是最大；

变化3：对于AC1的中点F，将点C看作位似中心，感觉F也在一半圆弧上运动，该半圆面与前述半圆面平行，且处在点C与半圆面之间的中间位置．

若利用几何画板画出动态图形，如图2，拖动点A1在其轨迹上运动，由位似观点可知点F到平面A1EB的距离恒为事实上，因为F是A1C的中点，故它到平面A1EB的距离为点C到平面A1EB距离的一半，所以恒为

初步判断选项A 错，C 对，B 与D 有待进一步探究．

二、理性分析论证

1.传统方法论证

如图3，显然题中A1E⊥DE,BE⊥DE，所以DE⊥平面A1BE，故有平面A1BE⊥平面BCDE．

图3

进一步地，在平面A1BE内过点A1作BE的垂线，垂足为H，在平面BCDE内过点H作CD的垂线HK，垂足为K，连接A1K，则∠A1KH即为二面角A1-DC-E的平面角．

连接CH，则∠A1CH即为直线A1C与平面EBCD所成角．

在Rt△A1HK中，的值不变（为），所以当A1H取最大值1时tan∠A1KH值最大（为），即锐角∠A1KH最大（为30°），所以二面角A1-DC-E最大（为30°）．

有疑问：是否仍然是点A1位于距平面EBCD最远处时，即A1E⊥BE时，直线A1C与平面EBCD所成角最大呢？

其实不然．在Rt△A1CH中，tan∠A1CH=当翻折角度超过时，A1H减小，CH减小，的增减无法判断．

敲黑板

可见并非点A1位于距平面EBCD最远处时直线AC1与平面EBCD所成角最大，看来对该选项的 “直观想象”导致了误判．

事实上，设二面角A1-ED-A的大小为θ，即∠A1EB=π-θ，则有向线段EH的数量为cosθ（与方向同向为正）．

故Rt△CKH中CK=2+cosθ，所以CH=

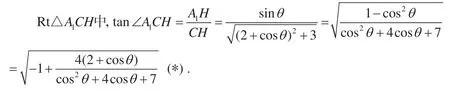
令t=2+cosθ,t∈(1,3)，所以(*)式

由基本不等式知，当t=即cosθ=-2时(*) 式取到最大值，相应的∠A1CH最大，即直线A1C与平面EBCD所成角最大．

2.向量法对选项D 的再分析

建立如图4所示的空间直角坐标系，记直线AC1与平面EBCD所成角为φ，设∠BOA1=α，则A1(cosα,0,sinα)，结合故

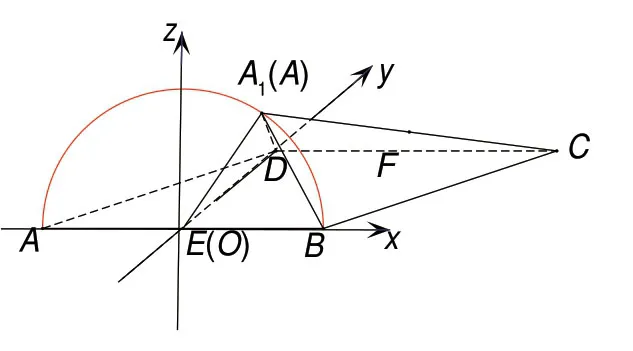
图4

又平面EBCD的一个法向量当即时取到最大值，即直线AC1与平面EBCD所成角最大．

三、对问题的再认识

再认识1：选项B 中，由于CD∥BE，当动点A1距平面EBCD最远时二面角A1-DC-E最大，但若CD与BE不平行，则结论并非如此．

再认识2：选项D 中，若取直线ED上的点C′（不同于点E），则也是当动点A1距平面EBCD最远时直线AC1′与平面EBCD所成角最大，可由（其中A1C′为定值）确定，但题中直线AC1与平面EBCD所成角则不然，影响其大小的两个量都在变化，需作图、推理、建模、计算．

证明：只需取A1D中点M，构造如图5中的平行四边形BEMF，即得BF长为定值．

图5

可见，合理运用恰当的思维就显得非常重要．

此外，结合上述分析过程，还可以直观感知BF也是一圆锥的母线，其长应为定值，如前图2．

练习：如图6，已知矩形ABCD中，AB=2,AD=4,E,F分别在线段AD,BC上，且AE=1,BF=3．沿EF将四边形AEFB翻折成A′EFB′，则在翻折过程中，二面角B′-CD-E的正切值的最大值为________．

图6

参考答案：如图7，设二面角B-EF-B′的大小为θ，作BG⊥EF于G，B′H⊥BG于H，则有向线段GH的数量为所以其最大值为当时取到．（可用两点连线的斜率数形结合解得，也可以利用辅助角公式）．

图7