基于历史结果缓存的路网k近邻查询算法
2021-02-11李佳佳杨亚星宗传玉夏秀峰
李佳佳,杨亚星,朱 睿,宗传玉,夏秀峰
(沈阳航空航天大学 计算机学院,沈阳 110136)
路网中的k近邻(kNearest Neighbor,kNN)查询是在给定被查询的兴趣点(POI)集合中,返回路网中距离查询点最近的k个POI对象。近年来,随着网络通信的发展,kNN查询成了一个重要的研究课题,引起越来越多学者的关注,在地图导航、救援服务、位置感知广告服务等方面具有广阔的应用场景,例如用户查找距离最近的酒店。
路网中每天存在大量的在线k近邻查询,现有研究中要么采用在线扩展路网的查询方式,要么采用基于索引结构的查询方式,通常关注基于单一查询效率的提升,而没有考虑大量集中查询的效率。如在学校、小区等区域比较集中的查询中,存在许多结果相似的查询,但每次都需要向服务器发起查询请求,重新进行k近邻查询,大大增加了服务器的负担。为此本文提出基于历史结果缓存的k近邻查询算法(Cache basedkNN,CBkNN),旨在重用缓存的历史k近邻查询结果,减少服务器的查询代价。
不同于现有的研究,本文研究的基于缓存的k近邻查询有以下特点:
(1)提出了共享前缀匹配模型,通过对缓存结果的共享匹配,提高缓存命中率。
(2)提出基于结点的缓存存储结构,快速查找可利用的历史查询结果,提高查询共享匹配效率。
(3)通过在真实路网中进行大量实验,结果表明,CBkNN算法比不使用缓存的INE算法快25%,比缓存算法MkNN响应时间少15%。
1 相关工作
目前对基于路网的k近邻查询算法研究或采用无索引的在线扩展方式,如INE算法、IER算法[1];或利用预先计算的索引结构来加快查找效率,如island[2]、S-GRID[3]、DisBrw[4]、ROAD[5-6]、G-tree[7-8]、TOAIN[9]等算法。前者只存储路网中节点和边的信息,需要大量在线计算;后者在存储基本路网信息的同时,需要预先计算一些节点信息,需要较长的预处理时间及较大的存储空间。2016年,发表在VLDB的文献[10-11]对以上算法进行了详细的实验对比,实验结果表明INE算法在POI密度较高的情况下性能较优。
基于INE算法,Thomsen等[12]提出了多步骤kNN查询算法(MkNN),通过历史结果的选择性存储,在下一步查询中重用存储的历史结果。MkNN算法中的历史kNN结果只起到辅助作用,减少了在线扩展路网中的节点,并没有直接回答新查询。同时,该算法依然存在INE算法的局限性,在POI稀疏的情况下,算法效率依旧较低。
文献[13]和[14]利用历史最短路径结果回答最短路径查询。通过子路径匹配,即在缓存的最短路径中匹配新查询的起点和终点,用于回答新的查询。文献[15]提出缓存路径规划(PPC)算法,与前者的仅当缓存与新查询完全匹配时才使用缓存的方法不同,PPC算法利用部分匹配的缓存路径来回答新查询的一部分,剩余部分重新查询。虽然基于缓存的最短路径算法并不能直接应用于kNN查询算法,但为本文研究提供了一些灵感。
综上所述,现有的kNN查询技术大多只关注单次查询效率,并没有考虑查询结果的重用问题。尽管有些工作提出了基于缓存的最短路径查询优化方式,但最短路径查询和kNN查询具有本质上的不同,并不能直接应用在kNN查询上。因此,研究基于缓存的kNN查询具有非常重要的意义。
2 问题定义
定义1路网。路网G由集合V、E和W组成,记为G(V,E,W),其中V{v1,…,vn}表示节点的集合,E{(vi,vj)|vi,vjV,i≠j}表示连接两个不同节点的边的集合,W={(vi,vj)|vi,vj∈V,i≠j}表示边的长度。图1所示为一个路网图。
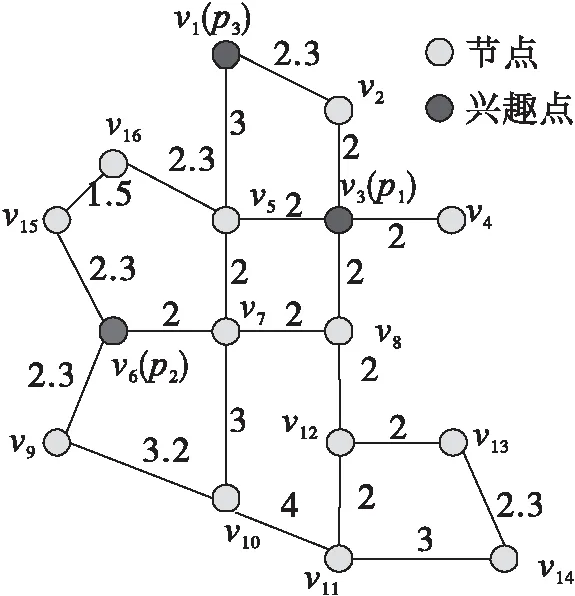
图1 路网图
定义2 路网k近邻查询。给定POI集合P和查询点q,返回路网中距离查询点q最近的k个POI的结果集合R,其形式化定义为:kNN(q)={p∈R, R⊆P|∀v∈P-R,dist(q,p)≤dist(q,v)}
定义3缓存C。缓存是kNN查询结果的集合。
定义4查询日志Qlogs。查询日志是由过去用户发布的带有时间戳的查询集合。
3 CBkNN查询框架
CBkNN查询框架主要分为k近邻共享检测、缓存结构、缓存管理和缓存命中k近邻结果计算,如图2所示。
当用户发起查询请求,首先需要查找共享检测产生的共享记录表,确定可以重利用缓存中的历史kNN结果。如果能够利用缓存结果,即缓存命中,则可以根据已有的历史kNN结果计算新查询的kNN结果,并返回给用户。如果不能重用历史结果,即缓存未命中,则需要向服务器发起查询请求,使用其它算法(INE)进行kNN查询来获取结果,同时需要更新缓存,对查询结果进行共享检测。
4 CBkNN算法
本文的主要目的是通过利用缓存的kNN查询结果来回答新的kNN查询,从而减少在线查询时服务器的工作量。最直接的解决方案是新查询和缓存的历史查询完全匹配,即历史查询点和新查询点相同,并且历史查询的k值大于等于新查询的k值,这种匹配通常被称为缓存命中;反之,称为缓存未命中。而在实际应用中,历史查询点和新查询点相同的情况并不多见,因此提高历史查询结果的重复利用是本文的工作重点。
4.1 k近邻缓存结果共享检测
引理1 给定查询点q,路网节点v和兴趣点p。如果p是q的k近邻结果之一,并且q到达p的最短路径经过v,那么p也是v的k近邻结果之一。引理1的示意图如图3所示。

图3 近邻共享
证明 假设p不是v的k近邻结果,那么dist(v,p)>dist(v,pk),pk表示第k个近邻结果。因为p是q的k近邻结果之一,即dist(q,p)≤dist(q,pk),p{p1,…,pk},q到达p的最短路径经过v,那么dist(q,p)=dist(q,v)+dist(v,p),所以dist(v,p)≤dist(q,pk)dist(q,v)≤dist(v,pk),与dist(v,p)>dist(v,pk)相矛盾,因此p也是v的k近邻结果之一。
基于引理1作进一步延伸,如果q到k个近邻结果的最短路径都经过v,那么q的k近邻结果也是v的k近邻结果。
定义5 共享前缀。给定路网节点q和v,以及POI集合P={p1,p2,…,pk}。如果P是q的k近邻结果,且q到前k′个近邻POI的路径经过v,其中1≤k′≤k,那么v是q的共享前缀,k′是共享结果值。
如图4所示,v2是v1的共享前缀。证明,已知v1的3NN结果是p1,p2,p3,v1到前2个近邻结果的最短路径都经过v2,即:
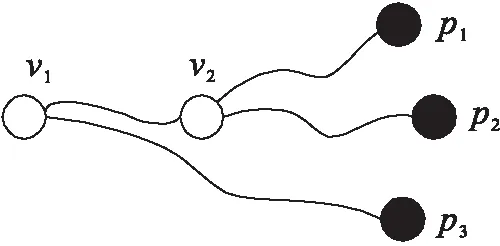
图4 共享前缀
dist(v1,p1)≤dist(v1,p2)≤dist(v1,p3)
(1)
dist(v1,p1)=dist(v1,v2)+dist(v2,p1)
(2)
dist(v1,p2)=dist(v1,v2)+dist(v2,p2)
(3)
由公式(1)(2)(3)可知,
dist(v1,p1)-dist(v1,v2)
≤dist(v1,p2)-dist(v1,v2)
(4)
即:
dist(v2,p1)≤dist(v2,p2)
(5)
那么p1,p2也是v2的2近邻结果,所以v2是v1的共享前缀。
通过对历史结果进行共享前缀检测,使更多的查询节点重利用历史结果,提高缓存命中率。首先,获取q的第一个近邻结果的最短路径;然后,依次获取路径上的节点v,确认其他近邻结果的路径是否经过v,确定v共享结果的个数k′;最后,将(q,k′,dist(q,v))放入缓存的共享记录表L中,其伪代码如算法1所示。
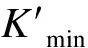

算法1:共享前缀检测输入:q,kNN(q)输出:L1.path1←kNN(q)//从kNN(q)中获取第一个近邻结果的路径2.forv∈path13.k′=0//共享值初始化4.for1≤j≤k5. ifv∈pathj//确定近邻路径中经过相同的节点v6. k′←k′+1;7. ifk′≥k′min8. L.v←(q,k′,dist(q,v))//将(q,k′,dist(q,v))加入v的共享表L中9.returnL
4.2 缓存结构
缓存结构包括历史查询日志表QLogs和共享记录表L。历史查询日志表存储历史查询的详细结果,共享记录表基于节点的存储结构,存储每个节点可以共享的历史查询集合,允许新查询快速查找历史查询日志表中可利用的历史结果。
历史查询日志表记录了历史查询点的详细查询结果,包括k个POI和查询点到POI的最短路径。其结构为:nodeID:r1,r2,…,ri,…,rk,其中ri的结构是ri:

表1 历史查询日志表
根据共享前缀检测算法,对于历史查询日志表中的每个记录,路径中的每个节点都能重利用历史结果。所以可以根据共享前缀检测算法对历史查询日志表中的每个结果进行共享前缀检测,同时共享记录表升序记录共享历史查询点和共享结果个数。共享记录表的结构为:nodeID:

表2 共享记录表
4.3 缓存的更新维护
由于缓存大小有限,因此在缓存已满时,必须删除某个使用效率低的历史k近邻查询记录,替换使用效率高的查询记录。本节通过探索路网中kNN查询的独特特征来提出一种新的缓存替换策略。
查询点的k值越大,查询结果中查询点到POI的最短路径经过的节点越多,查询结果中共享前缀节点可能会越多,同时k值越大,代表kNN结果能够服务的k值范围越大,那么历史结果被利用的可能性越大。因此,历史查询点的k值越大,历史结果被重利用的可能性越大,缓存的命中率越高。为了提高缓存的命中率,本文用k值较大的结果替换k值较小的缓存结果。当新查询点q的k值大于缓存中相同的历史查询点q′的k值时,用q的结果替换q′的结果,提高缓存的命中率。其算法的伪代码如算法2所示。

算法2:缓存构建和更新输入:q,kNN(q),C输出:C1.ifCisnotfullthen2. Insertq.resultintoC//放入缓存3. L←kNN(q)//q结果共享检测4. returnC5.else6. ifq.kq′.k,q′∈Cthen7. q′.result←q.result//更新缓存8. else9. C←LRU,LFU//LRU或者LFU策略更新10. L←kNN(q)//q结果共享检测11. endif12.endif13.returnC
4.4 CBkNN算法
基于共享前缀检测,更多的节点能够重利用历史kNN查询结果,提高了缓存命中率。为了方便讨论,本文对缓存命中的概念进行了如下定义:
定义6缓存命中。给定一个k近邻查询q,如果缓存中存在一个历史查询q′,q是q′的共享前缀,且共享结果值k′ ≥k,则称为缓存命中。
本文根据缓存的历史结果,计算新查询的kNN结果。由定义5可知,新查询到POI的路网距离计算模型为:
dist(q,pi)=dist(q′,pi)-dist(q′,q)
(6)
算法3展示了基于缓存的k近邻查询算法。步骤(1)为从共享表中获取查询共享的历史查询结果。步骤(2~3)是在缓存中查找共享的结果。步骤(4~7)是根据历史结果计算查询点q的k近邻结果。步骤(8)是在缓存未命中的情况下,使用其他方法计算查询的k近邻结果,并更新缓存和共享表。

算法3:基于缓存的k近邻查询输入:q,k,G,C输出:R1.qAC←L //从L中获取q的共享缓存结果2.ifqACØandk′k//获取第一个缓存历史点3. Rq′←Qlogs //获取qAC中历史查询k′值最大记录4.fori=1tok,pi∈Rq′5. dist(q′,pi),dist(q′,q)←Rq′6. dist(q,pi)=dist(q′,pi)-dist(q′,q)7. R←(pi,dist(q,pi))8.elseR←INE // INE方法计算结果,并更新缓存9.returnR
5 实验
5.1 实验参数
本文使用真实的德国奥尔登堡地图数据集对算法性能进行全面的评估。地图具有6 105个节点和7 035条边,如表3所示,实验的默认参数用加粗字体表示。其中缓存大小|C|是地图数据的12%。
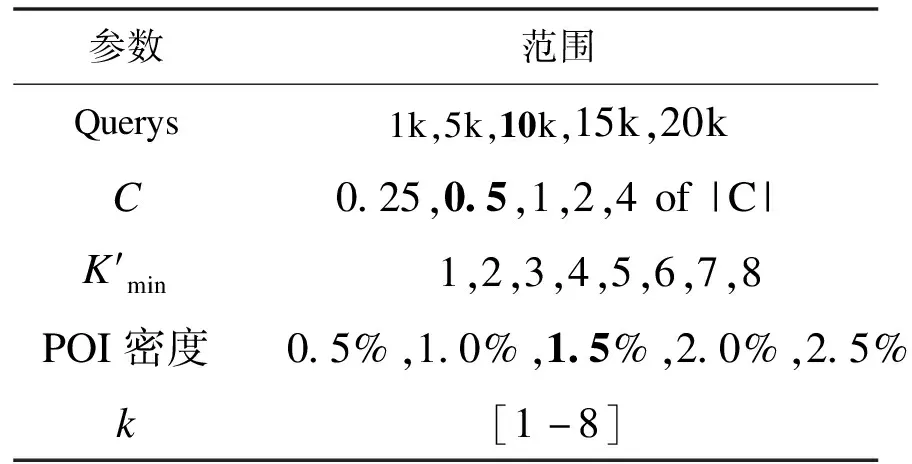
表3 实验参数
为了模拟真实情景,保证实验的真实性,本文在路网中设置集中查询区域,并随机模拟产生POI、查询点和查询k值。同时为了测试CBkNN算法的性能,本文使用了不同的缓存策略LRU(Least recently used)和LFU(Least frequently used)。LRU会将近期最不会访问的数据淘汰掉,LFU淘汰近期使用频率最小的数据。同时与INE和MkNN[1]算法进行比较,INE算法是非缓存算法,MkNN算法是重用历史结果的算法。文献[10]对非索引的kNN算法进行了详细的实验对比,INE算法的综合性能最优,所以本文的非缓存算法采用INE算法。基于缓存的最短路径查询算法[11-12]使用时间节省率和命中率作为评估性能的重要指标,所以本文主要比较两个性能参数:时间节省率和命中率。查询时间节省率是缓存算法相对于非缓存算法的节省时间的比值,其计算公式为

(7)
其中timeno_cache是没有使用缓存的INE算法响应时间,timecache是使用缓存算法的响应时间,时间节省率越大代表性能越好。命中率是缓存使用效率重要指标,命中率的计算公式为
(8)
其中hitcache是缓存命中的次数,Q是查询总数量。
5.2 实验结果
本文以INE算法作为基础对比实验,通过测量缓存命中率和时间节省率检测MkNN算法和CBkNN算法的性能,然而MkNN算法中每次查询需要使用多个缓存结果,并不能统计出缓存命中率,所以本文并不比较MkNN算法的命中率。每组实验只改变一个参数,其余参数设置为表3的默认值。通过实验,本文测量了多个参数对算法性能的影响。
(1)查询数量
图5展示了查询数量对算法性能的影响。从图5中可以看出,随着查询数量的增多,CBkNN算法的命中率和时间节省率都在提高,最终趋于稳定。这是由于查询数量较少时,缓存中的结果并不是集中区域的查询,所以缓存命中率较低,时间节省率也处于较低水平。随着查询数量的增加,缓存中的结果经过替换变成常用查询,命中率不断提高,查询时间节省率也不断提高。图5a中可以看出,查询数量到达5k和15k后,LRU策略缓存和LFU策略缓存的缓存命中率以及时间节省率都趋于稳定。
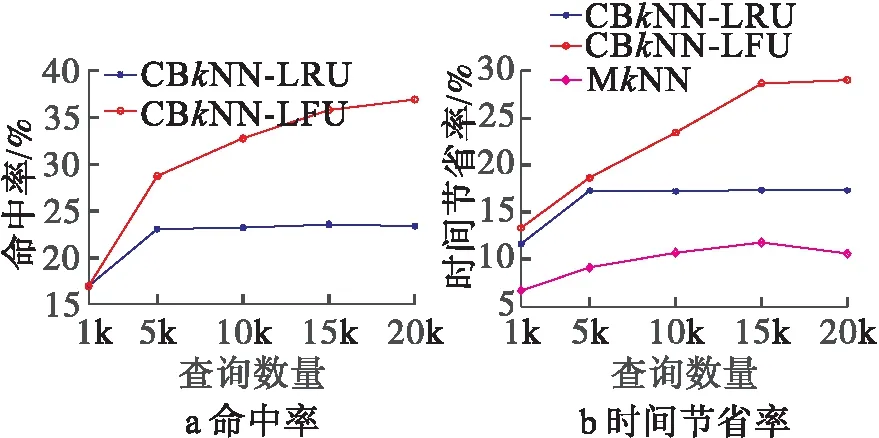
图5 查询数量
同时也可以发现,LFU策略的缓存性能优于LRU策略,这是由于查询集中频率较高的区域,LFU策略侧重于查询的频率,而LRU侧重于查询的最近时间。从图5b可以看出本文的CBkNN算法优于MkNN算法。这是由于MkNN算法只是使用历史结果作为候选结果,减少查询扩展的节点,而本文的CBkNN算法直接使用历史结果,减少更多的扩展节点。
(2)缓存大小
缓存的大小直接决定了系统可存储最大k近邻结果的数量,图6展示了缓存大小对算法性能的影响,可以看出本文的CBkNN算法性能最优。
从图6a中可以看出,随着缓存的增大,所有算法的缓存命中率在逐步提高。这是因为缓存越大,存储的历史结果越多,缓存中可以命中的查询越多,所以缓存命中率越高。

图6 缓存大小
图6b中可以发现,随着缓存的增大,查询时间节省率会逐渐减少。这是因为缓存增大,命中率提高,能够利用缓存直接得到更多查询结果,所以计算量减少,查询时间节省率提高。
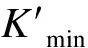
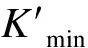
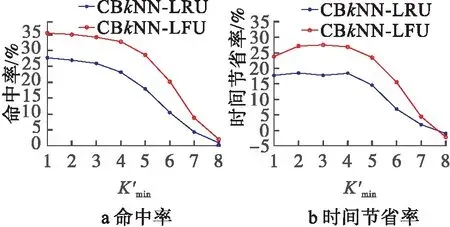
图7 共享最小k′值
从图7可知,共享最小k′值越大,CBkNN算法的命中率越低,查询节省时间率越低。这是因为对缓存中的历史结果进行共享匹配时,共享k′值越大,缓存中单个缓存能够共享缓存结果的节点越少,导致命中率降低,节省时间率降低。
(4)POI密度
图8为不同POI密度下的命中率和时间节省率。
从图8中可以看出,随着POI密度增加,CBkNN算法的命中率降低,查询时间节省率也随之降低。这是因为POI密度增加,查询点到POI的路网距离减小,单个缓存结果共享前缀节点减少,所以命中率降低,时间节省率也随之降低。
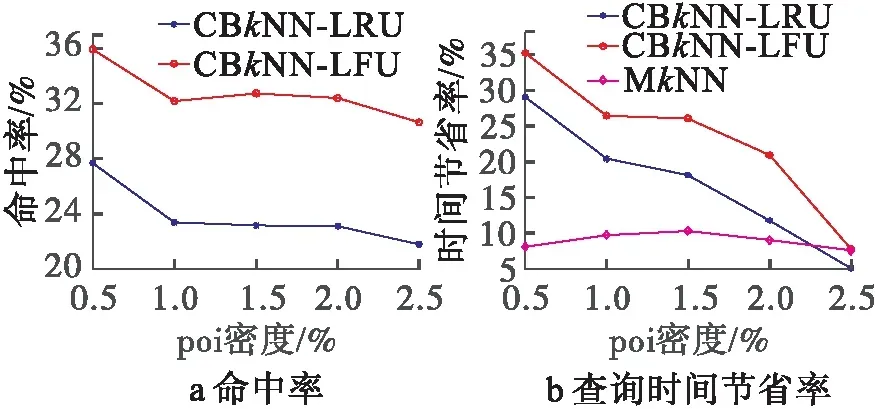
图8 POI密度
6 结论
本文提出了一种基于历史结果缓存的路网kNN查询算法,提出了共享前缀匹配模型,通过对缓存结果的共享匹配,提高缓存命中率。提出基于节点的缓存存储结构,快速查找可利用的历史查询结果,提高查询共享匹配效率。实验表明,本文的CBkNN算法与没有缓存的INE算法相比,系统减少25%的时间延迟,与缓存算法MkNN相比响应时间减少10%。
