基于赫兹理论的全方位MY轮稳定驱动分析

叶长龙，李延灼，陈 南，于苏洋

(沈阳航空航天大学 机电工程学院，沈阳 110136)

随着相关理论研究和运动控制的日渐成熟，全方位移动机器人广泛应用于工业制造和物流等行业[1-2]。全方位移动机器人的关键结构为承担全向运动的全方位轮,目前包括主动控制的万向轮、连续切换轮、麦克纳姆轮和MY系列全方位轮等[3-5]。MY轮外形类似于正交轮，2个MY轮通过串联或并联的方式构成全方位轮组来实现移动平台的全方位运动。在保证全方位运动的前提下，双球冠差动式MY轮有较好的承载能力和越障能力[6]。全方位轮本身的机械结构在实际的使用中存在抖动和打滑的问题[7-9]，主要是由MY轮在运动过程中轮子与地面接触区域产生，所以本文将详细分析双球冠差动式MY轮与地面的接触，并尝试从接触力学[10]的角度构建MY4轮的接触力学模型，为全方位机器人的稳定运动控制打下基础。

1 MY4轮接触力学模型

1.1 MY4轮机械结构

为实现重载条件下的全方位移动，本文设计了双球冠差动式MY轮简称MY4轮，由十字轴、凸台和双球冠构成，如图1所示。作为轮子支撑的主动轴和被动辊轴构成了十字轴。

图1 MY4轮

圆台安装在轮子内部，与球冠形成的内差动结构形成整体上的力封闭结构，如图2所示，该结构可以有效增加轮子的承载能力。

图2 力封闭结构

2个MY4轮并联布置，构成一个全方位轮组，如图3所示，通过齿轮传动，保证2个MY4轮绕十字轴的主动轴同步转动。在运动过程中，并联布置方式使2个MY4轮组单元能够连续交替地与地面接触，有效提供驱动力矩。

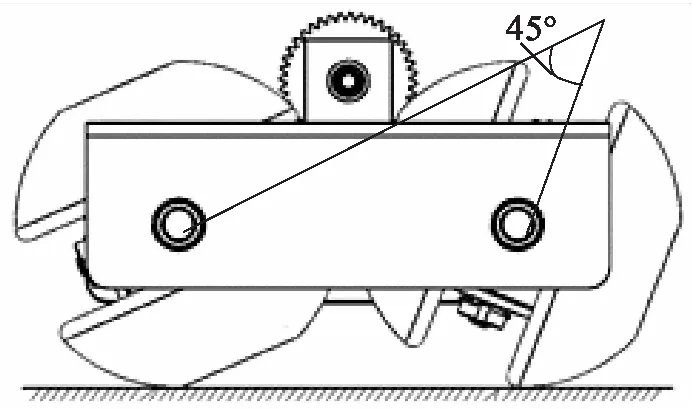
图3 全方位轮组

表1为双球冠差动式全方位轮的结构参数表。

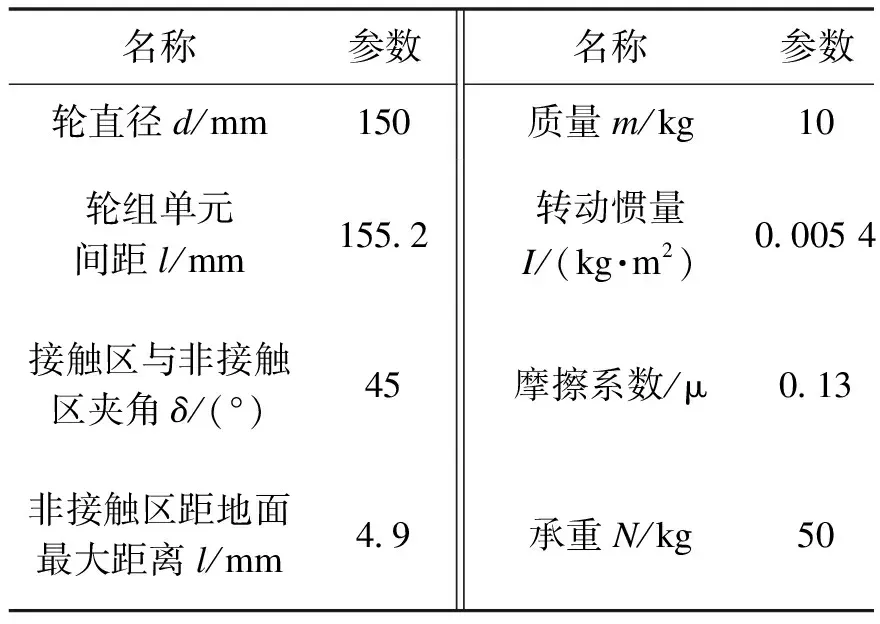
表1 MY4轮相关参数

1.2 MY4轮运动原理

图4为MY4轮的全方位运动简图,x方向为主运动方向，在该方向上MY4轮绕十字轴回转中心即主动轴旋转;y方向为侧向滑移方向即被动运动方向，在该方向上MY4轮球冠绕十字轴被动辊轴转动;在x-y平面上，x与y方向的复合运动使轮子在运动过程中存在2个正交的自由度。

图4 MY4轮全方位运动简图

MY4轮的使用方式类似于正交轮[11]，单个双球冠差动式轮子只能保证y方向的运动，在x方向上由于球冠顶部被切除，会形成接触区和非接触区，所以无法连续运动。2个MY4轮被动轴45°并联布置，使得接触区和非接触区相互错开，保证了与地面接触的连续性，实现了平面内的全方位运动特性，MY4轮采用并联排布的运动方式，轮组结构简图如图3所示。

1.3 MY4轮接触分析模型

带负载的MY4轮与水平地面接触时，由于轮体受载发生弹性变形，接触位置处并非是理想的点接触，而是面接触。当MY4轮处于静止状态时，施加法向载荷，轮子与地面的接触面为圆形。随着法向载荷的增加，MY4轮回转轴中心会沿法向接近圆形接触区，接触区的面积也会不断变大。在这一静力学模型中，几何尺寸较小的接触区是全方位运动生效的关键位置，接触位置处的几何与力学变量会很大程度影响MY4轮的机械性能，因此基于赫兹接触理论[12]建立MY4轮的静力学模型，推导法向载荷与相关变量之间的映射关系显得尤为重要。赫兹理论假设材料是完全弹性变形的，同时材料均匀，各向同性，接触表面光滑连续。以此构建MY4轮在受到法向载荷时的轮廓变形方程、弹性形变方程以及静力学平衡方程，联合推导出MY4轮接触静力学模型，便可导出负载、接触面半径和轮心与法向位移三者的映射关系。

1.3.1 静力学模型建立

假设MY4轮与一个弹性球面接触，MY4轮半径为R，弹性球半径为R0，并于O点处添加法向载荷使得两个球体压近接触。A、B两点距离对称中心均为d，如图5所示。MY4轮与弹性球接触而受约束，轮体的材料是均匀分布且存在弹性变形的，并假设球冠轮毂包覆的橡胶材料厚度远大于轮子受法向力时接触圆的半径a，故可视其为弹性半空间[13]。

图5 接触分析模型

依据赫兹理论推导在法向受载时MY4轮与弹性体的几何变形公式。

由弦长公式可得

R2=(R-z1)2+d2

(1)

在微变形条件下，可令MY4轮径向压缩量z1的高阶项为无穷小量。故上式展开后z1的二次项可忽略不计，可得

(2)

对于弹性球同样适用，因此当MY4轮上的载荷挤压固定不动的弹性球时，A、B之间的距离可表示为

(3)

设X1为MY轮A上一点因局部变形沿Z1方向所产生的位移，X2为弹性球B上一点因局部变形沿Z2方向所产生的位移，两球中心O1、O2的接近距离为δ。在接触区域内，则有

δ=z1+z2+X1+X2

(4)

联立(1)、(2)、(3)、(4)式可得

(5)

由轴对称性且两球形弹性体接触,根据接触,力学空间轴对称问题作用在面积单元dsdφ上的位移方程可得

(6)

(7)

其中，E1、μ1与E2、μ2分别为MY4轮与弹性球的弹性模量以及泊松比，p为赫兹压力分布，因此，MY4轮与弹性球圆心处的径向位移表示为

(8)

按照赫兹接触理论，接触区域的压力为抛物线分布形式，接触圆中点O处的接触应力压力最大Pm。接触区域边界处的法向压力为0，因此可得

(9)

其中，dsinφ为接触区域内部任意一点与接触区域中心的距离，如图6所示。

图6 接触区域建模

MY4轮因其机械结构特殊，在与地面接触时，可以将地面视为接触分析模型中半径无穷大的接触圆。根据赫兹理论，可以计算得到接触区域半径a、MY4轮法向形变δ和最大接触压应力Pm

(10)

通过理论计算得出，法向载荷P与接触圆半径a、MY4轮法向形变δ和最大接触压应力Pmax呈非线性关系，如图7所示。随着负载P的增加，在包覆橡胶材料不失效的条件下，接触圆半径a、MY4轮法向形变δ和最大接触压应力Pm的增大趋势逐渐为零。

图7 不同法向载荷下MY4接触形变与接触应力变化曲线

1.3.2 滚动接触

通过赫兹接触理论研究分析了MY4轮受法向载荷时有限范围内的接触状态，描述了系统静力学模型。为了更加精确地建立MY4轮的接触力学模型，还要考虑切向加载，将接触问题拓展至滚动接触[14]。

根据接触力学三维非协调接触滚动理论，当MY4轮在法向加载和驱动力共同作用时，MY4轮接触区域边缘会产生“微滑”现象，如图8所示。

图8 滚动接触分析模型

通过静力学分析可知，当MY4轮受载处于静平衡状态时，其与地面的有限接触域为一圆域。当驱动力矩通过十字轴传递到轮子上时，在接触位置产生的切向力会使轮体发生弹性变形，接触圆内MY4轮和地面的重合点会产生相对位移s。当极限摩擦阻力大于这个切向力且切向力不为零时，根据接触圆径向的不同力学状态，轮与地面的接触圆域会分化为两部分[15-16]，即“滑动区”和“黏着区”，几何形状上分别表现为宽度为s的环形区域和半径为c的圆形区域。其中，“黏着区”是MY4轮与地面相对静止的区域，“滑动区”是MY4轮与地面存在相对滑动的区域。

由静力学分析可知，当MY4轮的法向载荷不变时，轮与地面接触半径a也不变。随着驱动力矩持续增大,“滑动区”的环形宽度s向圆形接触区的圆心不断扩大；“黏着区”的半径c不断向圆形接触区的圆心收缩。某一时刻，“黏着区”收缩至接触圆的圆心处成为一个点，此时滑动区扩大为圆形接触区域的去心邻域，MY4轮处于完全打滑边缘状态。

MY4轮在驱动力和摩擦阻力所构成的力偶作用下会产生垂直于接触面法线(图8中所示点划线)方向的微变形。图8中虚线表示MY4轮球冠处弹性材料在力偶作用下发生的法向变形趋势,在这种趋势下，MY4轮与地面的接触区与静力学分析时的圆形接触区不同，因此认为“黏着区”是实际为轮子提供驱动力的区域。

根据接触力学相关基本理论推导驱动力同实际有效接触区半径c之间的关系。在负载P的作用下，MY4轮与地面间产生一个圆形的接触面，其半径的大小由式(10)确定。

MY4轮的驱动力是关于图5所示平面对称的，在这种情况下“黏着区”仍然为圆形并与接触圆同心。

忽略切向力在法向上的影响，当MY4轮和地面原点处接触时，切向力的分布为

q′(x,y)=μp(x,y)=μPm(1-r2/a2)1/2

(11)

式(11)中，q′(x,y)为法向载荷作用下接触面产生的切向力；μ为MY4轮与地面摩擦系数；r为接触区域内一点距离接触中心的径向距离。

MY4轮加载驱动力矩时，“黏着区”内的切向力分布为

(12)

式(12)中，q″(x,y)为驱动力矩作用下接触面产生的切向力。

根据接触力学理论，“黏着区”半径c的数值大小可由切向力计算得到

(13)

整理可得“黏着区”与接触圆半径a的数学关系

c=a(1-Q/μP)1/3

(14)

由此得到MY4轮的有效驱动面，即半径为c的圆形区域。

令μP=60 N，接触面切向力Q与打滑程度即c/a之间的函数关系如图9所示。当轮子有效驱动力矩达到“饱和”时，轮子将处于完全打滑状态。

图9 不同打滑程度下切向力变化曲线

从图9中分析得出，在c/a=(0,0.4)时，切向力的变化范围约为(56,60)，相对于切向力Q，c/a变化梯度为0.1；在c/a=(0.4,1.0)时，切向力的变化范围约为(0,56)，相对于切向力Q，c/a变化梯度约为0.01。

因此，保证c/a的变化范围在(0.4,1.0)，即使外部干扰造成切向力的突然增大，轮子依然可以提供有效的驱动力而不发生滑动。

2 MY4轮驱动稳定性分析

全方位轮的驱动力大小主要取决于越障高度和轮子运动时反力矩的大小，现在讨论MY4轮在理想平面运动时的稳定驱动力矩。

由MY4轮接触力学分析可知，驱动力矩M产生的牵引力(切向力)作用在轮与地面的接触面时存在半径为c的有效驱动面。为保证驱动力矩的有效性，忽略轮与地面的粘连形成的拉力及空气阻力，即轮子与地面不存在打滑现象时“黏着区”的大小为

(15)

驱动力矩M(驱动力矩等于轮组即将运动时接触区域边缘产生的反力矩与系统摩擦力矩MS之间的阈值)大于等于接触面静摩擦产生的有效驱动力矩与系统摩擦力矩Ms时才会使机器人产生有效运动。因此可得关系式

在临界条件下，电机启动力矩要大于滚动摩阻M1与系统摩擦力矩之和

M≥M1+Ms=P*a+Ms

(16)

为保证有效驱动c>0，即驱动力矩的阈值为

(17)

通过式(17)可以得到稳定驱动时驱动力矩M的数值取值范围。分析可知，在载重不变的条件下，轮子打滑是由于提供有效驱动力“黏着区”的范围随着驱动力矩的增大逐渐减小。

根据表1中MY4轮的参数，在法向载重P=50 kg；经计算有接触半径a=0.007 08 m，角加速度为50 rad/s2,并假设Ms=0时，电机驱动力矩M的取值范围为：0.35

3 仿真与实验

3.1 MY4轮静力学仿真

通过ANSYS对MY4轮进行静力学仿真，MY4轮外包覆橡胶材料属性如表2所示。

表2 接触材料属性

对仿真模型进行如下简化：地面与轮子的接触设定为摩擦接触，其余机械结构接触面设定为bonded接触模式，即视为一个焊接件；去除三维装配体中的圆角和倒角，将轴承零件使用圆柱实体代替以减少网格划分的难度；轮子的半径R=75 mm。根据圣维南原理将十字轴两端所受的轴承力简化为轮子中心点处的法向力，并去除未与地面接触的球冠。

图10a为ANSYS仿真结果与理论计算结果，其中，横坐标为轮子法向压力P，纵坐标为接触面最大接触应力值Pm。

图10 MY4轮接触仿真

从仿真结果来看，相对于理论值，进行了模型简化的MY4轮的静力学仿真存在一定的误差,但其变化趋势与理论值一致。

3.2 MY4轮静力学实验

MY4轮的静力加载实验验证接触力学静力学模型的准确性。本实验中，地面的材料属性与仿真实验时选取的材料属性一致。首先取单独MY4轮作为加载对象并使之处于静止状态，沿MY4轮法向加载测得MY4轮的轮地接近距离H(MY4轮法向高度变化)。

静力加载实验利用控制变量法定量增加MY4轮法向载荷，并记录每次加载后对应的地面接近距离H的大小，对得到的数据点进行多项式曲线拟合，如图11所示。

图11 MY4轮法向加载实验

在单独MY4轮静力加载实验基础上，以重载全方位移动机器人为实验对象，通过法向加载不同质量的重物统计移动平台接地距离，并进行数据处理，如图12所示。

图12 法向加载实验

从两次实际工况下的试验曲线可知，随着法向载荷逐渐增加，MY4轮的接触变形符合静力学模型公式的非线性变化规律。

3.3 MY4轮驱动打滑试验

在MY4轮驱动打滑试验中，通过改变电机的加速度来实现不同的驱动力矩加载，MY4轮表现出不同运动状态。试验结果表明，当电机加速度为50(运动状态1)时，MY4轮没有明显的打滑现象；当电机加速度调整为100(运动状态2)及150(运动状态3)时，MY4轮在启动过程中有明显的打滑现象。

图13为不同运动状态下电机实际电流变化曲线。通过比较各个状态下电机实际电流变化趋势可知，当MY4轮打滑时，电机反馈电流在电机启动过程的某一时刻会有一个突变，即图中的电流变化趋势线。当MY4轮越过打滑点时，实际电机电流变化趋势线将逐渐与实际检测电流曲线重合，与理论分析一致。

图13 MY4轮打滑实验

4 结论

本文基于赫兹接触理论，对MY4轮在法向载荷作用下与地面之间的接触力学进行建模与分析，通过有限元仿真及静力学加载试验论证了接触模型的正确性。分析结果表明：

(1)最大接触应力并不随负载的增加而线性增加，这种梯度递减的变化有利于重载条件下保障MY4轮外部包覆材料的有效性；

(2)当法向载荷增大时，接触面半径不会因负载的增大而线性增加，保证了MY4轮的启动力矩大小不会随负载线性地增大，有利于保证MY4轮机械系统的驱动效率；

(3)轮心与地面接近距离的立方同负载的平方成正比，随着负载的增加机器人底盘不会线性地随负载增大而沉降。

(4)在MY4轮与地面滚动接触时，“黏着区”为轮子提供了有效的驱动力，并且在轮子法向载荷不变时，随着驱动力矩的增大“黏着区”呈非线性减小趋势。因此可以得到MY4轮提供有效驱动的驱动力矩的参考范围。在基于MY4轮的全方位移动平台的控制中，根据轮子与地面滚动接触特性建立准确的机器人运动模型,进而为提高机器人的运动控制稳定性和有效驱动提供设计依据。