毛细管内气体泄漏特性的实验与理论分析
2021-02-10王辉邢继孙中宁王一博
王辉, 邢继, 孙中宁, 王一博
(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001; 2.中国核电工程有限公司, 北京 100840)
压水堆核电厂严重事故期间堆芯熔化,释放大量放射性裂变产物进入安全壳,这些裂变产物以气体或气溶胶的形态在安全壳内输运,当安全壳失效时,这些裂变产物将释放到外界环境,威胁公众安全。即使安全壳未被破坏,这些有害物质仍可能经由混凝土安全壳缝隙、墙体与管道接口缝隙、阀门旁路等窄缝通道进入大气环境,给周边人员及环境带来影响[1]。传统的安全分析假设气溶胶泄漏率和气体泄漏率相等,并未考虑到缝隙对气溶胶的滞留作用,因而该假设是保守的[2]。为降低严重事故放射性后果计算中的保守性和不确定性,学者开展了缝隙内气溶胶的滞留特性的实验和理论研究[3-5],研究表明:安全壳缝隙对气溶胶颗粒具有很强的滞留作用,与气体泄漏率相比,气溶胶的泄漏率会显著降低。Morewitz等[6]提出直接根据缝隙的当量直径来预测气溶胶的泄漏率模型。Nelson等[7]对毛细管内气溶胶滞留开展了实验研究,发现毛细管内气溶胶甚至会出现堵塞。缝隙内气溶胶的沉积受多种机理影响,如重力沉降、布朗扩散、湍流扩散和湍流碰撞,当缝隙表面温度远低于气体温度时,还存在着热泳沉积,当气体含有水蒸气且在缝隙表面冷凝时,也存在着扩散泳沉积等。为快速计算缝隙内气溶胶的穿透及滞留系数,研究人员基于实验和理论分析,总结了一系列关系式。Fuchs[8]利用流动函数的概念得到了颗粒穿透缝隙的模型,该模型考虑了重力沉降。Walton[9]和Pich[10]分别提出了相同的计算模型,由于该方法仅考虑重力沉降,对于亚微米级颗粒而言,扩散沉积不可忽略,因此该方法仅适用于微米级粒子的计算,不适用于亚微米级的计算。文献[11-12]分别建立了缝隙(毛细管内)的气体流动和气溶胶输运与沉积理论模型,前者考虑了层流、湍流和临界流动的情形,而后者主要针对层流情形,在一定假设条件下,二者均可以分析缝隙(毛细管)的堵塞行为。Williams[13]进一步完善模型,考虑缝隙内水蒸气的蒸发和冷凝,分别针对不可凝气体、水蒸气和气溶胶建立了质量、动量和能量守恒方程,缝隙内气溶胶的沉积机理考虑了重力沉降、热泳沉积、扩散泳沉积和不同的湍流过程。综上所述,无论微通道内气溶胶泄漏率实验结果,还是理论模型中气溶胶去除机制的选择,都需要以微通道内气体的流动状态为基础,张志弘等[14]更进一步提出了利用气体泄漏率和泄漏孔长度估算气溶胶泄漏率的方法。现有关于微通道内流动特性的研究多为低压差情形,而在严重事故下,安全壳内压力较高,安全壳外则为大气压,缝隙两侧压差较大,因此缝隙内流速较高,马赫数较大,甚至会达到壅塞状态,而另一方面由于通道尺度较小,缝隙内流动的雷诺数较低,流动的层流化现象比较明显,这些与常规尺度通道内的差异都会影响到气溶胶的滞留特性。
本文以规则几何结构的毛细管作为微通道的代表,通过针对不同尺度的毛细管,1~500 kPa压差范围内开展毛细管内气体泄漏特性研究,分析毛细管微通道两端压差与气体泄漏率及微通道内流动特性的关系,同时可以获得不同特征尺寸微通道内气体的泄漏特性,为工程中复杂通道内气体泄漏率的计算评估提供理论依据。
1 泄漏特性实验装置和数据处理
1.1 实验装置
毛细管内气体泄漏特性实验装置如图1所示,该装置主要由压力容器、空气供应系统、壁温控制系统、气溶胶配送系统和缝隙泄漏实验段等部分组成;压力容器是实验系统的主体,毛细管的上游利用压力容器模拟安全壳,压力容器内可以实现空气和气溶胶的均匀混合和上游压力的恒定。毛细管下游为大气压,从而可以实现毛细管两端压差和气体组分的改变。空气供应系统与压力容器相连可以提供实验所需的空气,壁温控制系统用于维持壁温和容器内温度的恒定。此外在压力容器的外壁装有贯穿件,可以用来连接毛细管实验件。

图1 毛细管内气体泄漏特性实验装置Fig.1 Experimental setup for characteristics of gas leakage through capillary tubes
实验选择了8种不同内径的毛细管,内径分别为25、50、75、100、150、175、200、300 μm,毛细管长度为10 cm。所选毛细管的内径公差随着内径的不同略有不同:25 μm内径毛细管的公差是±1 μm;50~175 μm内径毛细管的公差是±3 μm;200~300 μm内径毛细管的公差是±5 μm。毛细管微通道采用卡套与密封环配合的方式进行连接固定,并且可以通过螺纹或者法兰与压力容器相连,实现毛细管实验件的更换。
缝隙泄漏实验段如图2所示,由压力容器表面贯穿件引出一条管道,管道接球阀,球阀控制整条回路的开关,球阀之后接毛细管实验件。毛细管的下游与集气罐相连,集气罐用来收集泄漏的气体。集气罐另一出口连接U型管压力计,使用U型管压力计测量集气罐内部压力的变化,通过压力的变化可以计算出不同工况下从毛细管泄漏出来的气体量。毛细管和集气罐为安装有温度控制系统,用于控制实验过程中毛细管和集气罐内温度的稳定。实验过程中集气罐内压力的升高会改变毛细管两端的压差,从而影响压差和泄漏率的对应关系。因此为避免集气罐内压力升高所带来的影响,实验测量中控制集气罐内压力的变化小于压差的0.5%,从而可以忽略压力升高给压差带来影响。由于不同压差下泄漏率不同,为确保每次实验有足够长的测量时间,集气罐有不同的体积,用于改变其内部压力的变化速度,控制达到限定压力的时间,方便实验测量。
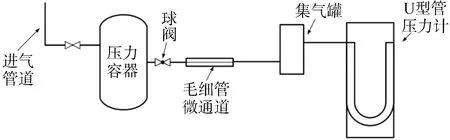
图2 缝隙泄漏实验段Fig.2 Experimental section of leakage
1.2 数据处理方法
压力容器中的气体通过毛细管通道泄漏出来,其泄漏率可以利用毛细管通道内气体的质量流量或体积流量表示。由于缝隙尺寸较小,相应的气体流量也较小,目前暂无流量计的测量范围能达到如此小的量级,本文采用压差法结合理想气体状态方程进行微小泄漏流量的测量。毛细管的上游为压力容器,毛细管下游设置集气罐,集气罐是一个密闭的圆柱形容器,容积为Vcol,容器上部设置有温度和压力传感器。初始状态时,集气罐内具有一定压力P1和温度T的气体;当毛细管通道泄漏的气体进入集气罐时,腔室内的压力会逐渐升高,待压力升高一个微小量ΔP后,达到终止状态P2。根据理想气体状态方程,可以推算获得泄漏气体的总质量Δm:
ΔP·Vcol=(P2-P1)·Vcol=Δm·Rg·T
(1)
式中Rg为气体常数。
再结合通气时间t即可得到毛细管通道内泄漏气体的质量流量Qm:
Qm=Δm/t
(2)
在测量泄漏气体流量的同时记录缝隙实验段两侧的压差以及混合气体组分的数据,进一步拟合泄漏流量与压差和气体组分之间的函数关系。
2 泄漏流量理论分析
低压差下毛细管内流动大多数为层流,目前计算毛细管内气体泄漏特性多采用基于层流推导得到的哈根-泊肃叶公式[15]。层流时管内径向速度分布为:

(3)
式中:v为速度,m/s;R为管道半径,m;r为距管道中心线的距离,m;μ为气体动力学粘度,Pa·s;dp/dz为压力梯度,Pa/m。
对式(3)在管道截面上进行积分,可以得到:

(4)
式中Qv为气体体积流量,m3/s。
气体质量流量为:
Qm=ρ·Qv
(5)
式中ρ为气体密度,kg/m3。
基于理想气体假设,进一步有:
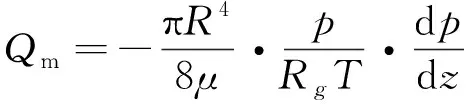
(6)
当气体在管道内的压降较小,可假设气体温度不变,即等温流动,此时有:

(7)
式中:L为管道长度,m;pi为管道入口压力,Pa;po为管道出口压力,Pa。
则毛细管内泄漏气体的质量流量有:
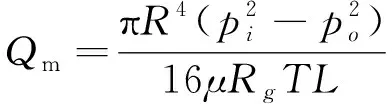
(8)
3 泄漏特性实验结果分析
3.1 泄漏率随压差的变化关系
图3和图4给出了不同内径毛细管内气体泄漏的质量流量随其两侧压差的变化关系,同时将不同压差下泄漏流量的实验值与经典理论公式的计算结果进行了对比。可以看出,内径小于100 μm的毛细管随着毛细管两端压差的增加,泄漏的质量流量增加较快,近似呈二次方增长。并且通过计算值与实验值的对比也可发现,式(8)可以较好地预测毛细管内泄漏的质量流量,两者间的相对误差大部分在10%以内,只有内径100 μm的毛细管,在压差达到500 kPa时开始出现变大趋势,预测偏差达到36%。而分析内径大于100 μm的毛细管内泄漏流量可以发现,当压差较小时,泄漏流量随压差增大依然呈二次增长趋势,且与理论预测值比较接近,然而随着压差增加到某一值后,泄漏量的实验值上升趋势变平缓,近似线性增长,并且开始偏离理论计算曲线。根据图4(a)进一步对比可知,随着毛细管直径的增加,发生转变时的压差变小,当毛细管内径为150 μm时,在小于300 kPa之前的实验值与理论值之间的相对偏差在5%~10%;而从大于300 kPa数据开始较大地偏离理论公式。对内径175 μm的毛细管,在小于200 kPa的数据偏差在10%左右,从大于200 kPa开始较大地偏离理论公式。此后,更大的毛细管内径分别在不同的压差下出现有不同程度的偏差,比如:内径为200 μm和300 μm的毛细管,则分别在100 kPa和80 kPa时出现了实验值与理论计算值的偏离。

图3 小内径毛细管内泄漏特性Fig.3 The leakage characteristics of capillaries with smaller inner diameter

图4 大内径毛细管内泄漏特性Fig.4 The leakage characteristics of capillaries with larger inner diameter
总结来看,内径25、50、75 μm的毛细管未出现偏离理论公式的情况,内径100~300 μm的毛细管出现偏离理论公式的情况,并且随管径的增大,出现较大偏离的压差也逐渐变小。通过分析认为该偏离现象可能与管内流体的流动状态有关,因此需要对雷诺数进行进一步分析。
3.2 雷诺数随压差的变化关系
雷诺数是判别流体流动状态的依据,在管流中,通常雷诺数小于2 300的流动为层流,雷诺数等于2 300~4 000的流动为过渡状态,雷诺数大于4 000的流动为湍流。图5和图6给出了毛细管内雷诺数随压差的变化规律。随着压差的增加,毛细管内流速增大,雷诺数也增加。内径小于150 μm的毛细管,其雷诺数都小于2 000,因此其内的流动状态主要以层流为主;内径175~300 μm毛细管通道,随着压差的增加,其内流动状态会从层流过渡到湍流状态。分析大直径毛细管的从层流过渡到湍流的临界雷诺数发现,随着毛细管内径的增加,临界雷诺数所对应的压差变小,内径175 μm的毛细管,在300 kPa附近发生层流到湍流的过渡,内径200 μm和300 μm的毛细管,分别在200 kPa和100 kPa附近出现过渡。
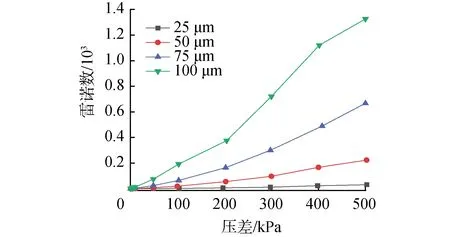
图5 小内径毛细管内的雷诺数Fig.5 The Reynolds numberin capillaries with smaller inner diameter
将图6与图4进一步对比分析发现,临界雷诺数所对应的压差与泄漏流量发生偏离时的压差并不一致,泄漏流量偏离时所对应的压差更小一些,这表明在发生层流到湍流过渡前,泄漏流量的实验值与计算值已经开始发生偏离,甚至对于150 μm毛细管而言,流动状态一直处于层流,但在300 kPa附近时泄漏流量也发生了偏离,这说明流态转变并非造成该偏离的唯一原因。
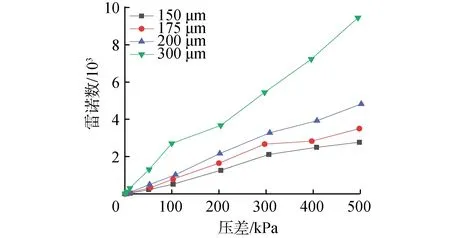
图6 大内径毛细管内的雷诺数Fig.6 The Reynolds number in capillaries with larger inner diameter
3.3 马赫数随压差的变化关系
为进一步分析毛细管内气体泄漏特性及流量偏离出现的原因,图7给出了不同压差下毛细管内平均马赫数的变化规律。随着毛细管两端压差的增加,毛细管内流速增大,因此毛细管内的平均马赫数也会相应增大;但当马赫数增加到某一值后,增加趋势会变平缓甚至停止增长,此时毛细管两端压差增大对马赫数影响不大,而主要是影响密度进而使泄漏流量增加,毛细管内表现出壅塞特征,气体的可压缩性影响变得显著。从图7中还可以看出,对于较大内径的毛细管,马赫数过渡发生的比较靠前,比如:直径300 μm毛细管在压差100 kPa,马赫数0.3附近时,马赫数的增长趋势开始变缓,即在较小的压差下出现过渡,且过渡时所对应的马赫数较大。随着毛细管内径的减小,发生过渡时的压差增加,平均马赫数降低,如直径150 μm毛细管在压差300 kPa,马赫数0.25附近时,马赫数的增长趋势开始变缓。由于内径和流速较低,所以在这种情况下马赫数发生过渡时,毛细管内甚至处于层流状态。尽管内径为150 μm的毛细管在300 kPa时流动为层流,但毛细管内的马赫数已经从增长区过渡到平滑区,即流体的可压缩性影响已经变得很显著,这也是造成泄漏流量实验值与理论值发生偏离的主要原因。针对更小的100 μm毛细管,可以看到在压差达到400 kPa时,马赫数也进入到平滑区,这也导致了图3(c)中泄漏流量的初步偏离。综上所述,在大压差毛细管泄漏特性分析时要考虑流体可压缩性的影响。
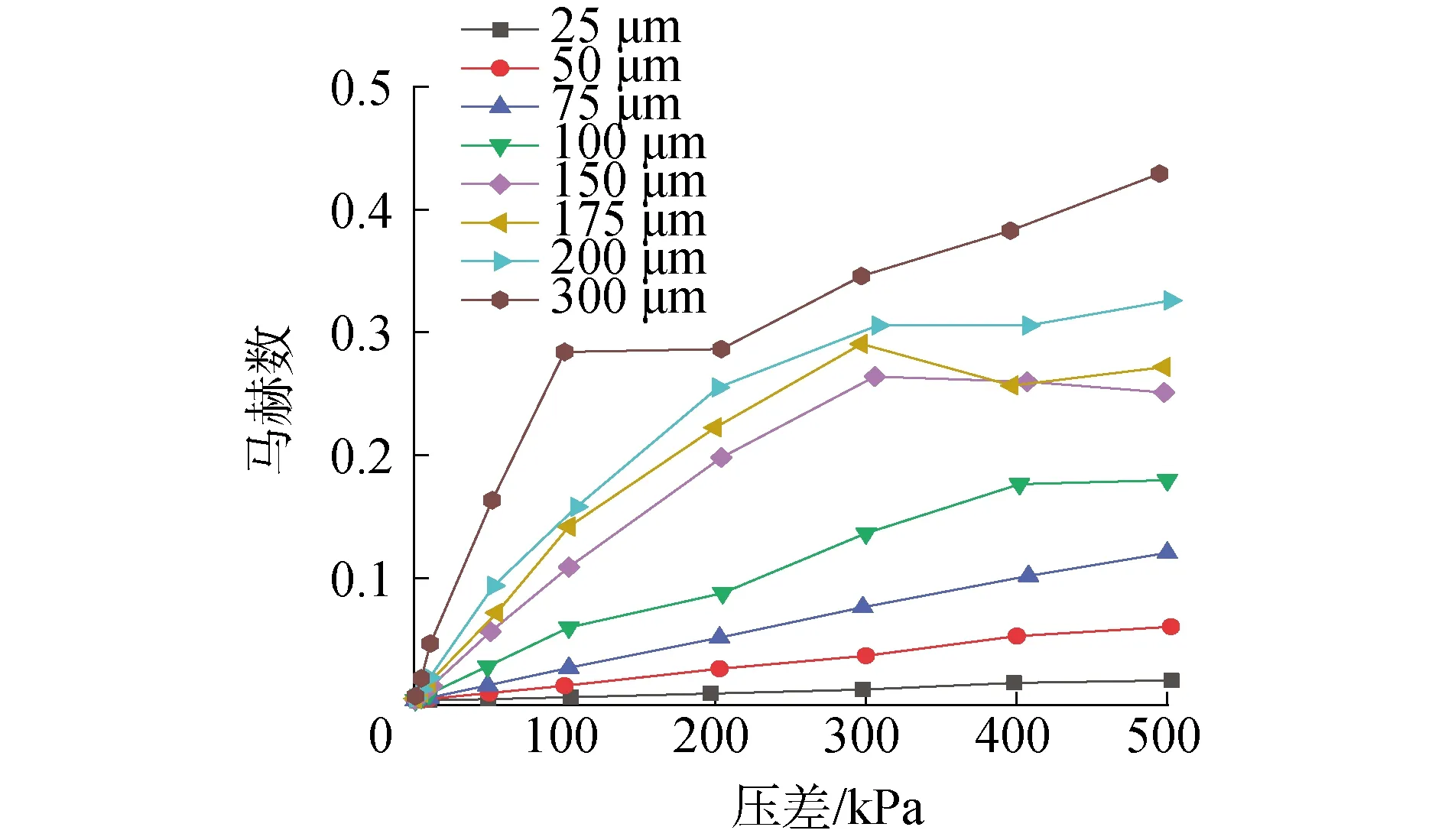
图7 毛细管内的马赫数Fig.7 The Mach number in capillaries
4 结论
1)毛细管内泄漏流量随压差的增加呈现出不同的变化规律。当内径小于100 μm时,随压差增加泄漏流量近似呈二次方增长,当内径大于100 μm时,压差超过某一值后泄漏流量增长趋势会向线性化过渡。
2)在小于500 kPa的压差范围内,内径小于150 μm的毛细管通道内主要处于层流状态,内径150~300 μm毛细管通道内流态会从小压差的层流到大压差下的湍流状态过渡。
3)随着毛细管两端压差的增加,毛细管内平均马赫数会从增长区过渡到平滑区,进入平滑区后马赫数基本不变或增加缓慢,表现出流动壅塞特征。此时,毛细管内流体的可压缩性影响变得显著。毛细管直径越小,发生过渡时的压差越大,平均马赫数越低。在小直径毛细管内过渡还能发生在层流区域。
4)当毛细管内流态处于不可压缩层流流动时,哈根-泊肃叶公式能够准确地预测毛细管微通道内的泄漏率。但当气体可压缩性较为显著时则需要利用微通道内流动方程对泄漏特性做进一步分析。
