某铜矿深部矿体采场结构参数优化研究

2021-02-10戴超群桂祖辉郑九文

铜业工程 2021年6期

戴超群，桂祖辉，郑九文

（铜陵有色金属集团股份有限公司安庆铜矿，安徽安庆 246000）

1 引言

某矿使用上向水平分层（进路）充填法进行开采，矿房和矿柱垂直矿体走向布置，采场长度为矿体水平厚度。在开采浅部资源时，采场跨度随矿体稳定性差异而改变，当矿体稳定性较差时，采用断面规格为3.5m×3.5m的进路式回采方案；当矿体稳定性较好时，对采场跨度进行适当地扩帮处理，扩帮后的采场跨度在4～5m。采准工程的布置从主斜坡道经分段联络巷进入分段巷，再通过分层联络巷和采场联络巷进入采场［1-2］，其采矿方法示意图如图1所示。

图1 上向水平分层充填采矿法示意图

随着矿山开采深度的增加，矿体节理发育，但整体稳定性却优于浅部矿体，如果一直沿用浅部矿体所用的机械化上向水平进路（分层）充填法的采场结构参数，将会导致深部矿体开采成本的大幅增加、贫化率过高等问题，房智恒［3］综合运用Mathew稳定图法和集成技术对初步拟定的两种开采方案形成的空场进行稳定性评价，结果表明Mathew稳定图法与数值模拟结论相一致。Smith P. F.［4］结合Mathews稳定性图与Barton极限跨度理论，为有效进行采场结构参数优化提供了一种方法。本文针对矿山深部矿体的赋存条件，通过理论计算，选用合理的采场结构参数有效降低高应力带来的各种危害［5-6］。

2 采场极限跨度理论计算

常见的计算极限跨度的方法有普氏压力拱理论、载荷传递交汇线理论和Mathews稳定图表方法等［7-8］。本论文采用以下三种方法，并将所得结果进行对比分析，得出最终极限跨度。

2.1 普氏压力拱理论

当冒落岩体可以视为具有一定凝聚力的松散体时，由普氏地压理论得知，在形成巷道或者采空区后，其顶板岩体会形成抛物线形的压力拱。采空区未破坏时，处于自然平衡状态。岩石发生位移、变形，从而形成压力拱，其采场跨度可根据式（1）计算得出［9］。

式中：w为采场跨度，m；b为顶板厚度，m；H为采场最大高度，m；f为普氏系数；φ为岩体内摩擦角。

需要注意：在运用上式求采场跨度时，选取的顶板厚度b应满足式（2）：

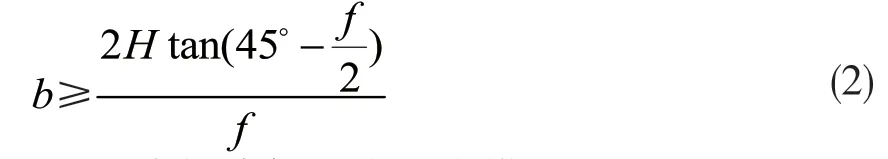
此时，才能确保形成压力拱。

2.2 载荷传递交汇线理论

载荷传递交汇线法规定：当传递线的位置在顶板与采场的两端交点以外的时候，端部位置直接承受来自于顶板上的外载荷和岩石的自重两方面的压力，此时认定顶板处于稳定状态［10］。顶板厚度与矿房跨度之间的计算公式为：

式中：w为采场跨度，m；b为顶板厚度，m；α为荷载传递线与顶板中心竖直线之间的夹角，一般取30°。

2.3 厚跨比理论

厚跨比理论定义的顶板安全准则为：顶板的厚度与跨度之间的比值应该大于等于0.5，如式（4）所示［10］：

即：

式中：w为采场跨度，m；b为顶板厚度，m；n为安全系数。

3 结果汇总

运用上述方法计算采场的极限跨度，首先需要确定顶板厚度、普氏系数、岩体内摩擦角、安全系数等参数。在本矿山中，上述公式中所涉及的参数如表1所示。

表1 跨度计算所需参数

通过表1中参数计算得出的极限跨度只是理论值，缺乏对现场地压、节理等因素的综合考虑。文献［11］中，唐亚男等利用弹塑性力学、厚跨比理论和载荷传递交汇线理论对顶板跨度进行了理论求解，再利用UDEC软件对4m、6m、8m和10m四种跨度进行了位移场和应力场分析，结果得出数值模拟的合理跨度与理论计算跨度之间存在0.86～0.99之间的修正系数。根据文献［11］，考虑到深部开采的高应力和节理发育等复杂情况，在本论文中修正系数取0.7～0.9之间。具体计算结果如下表2所示。最终本方案中矿房和矿柱跨度选择为6 m，并且沿着矿体走向交替布置，分层高度为4 m，采场长度为矿体水平厚度。