穆利亚希南露天边坡稳定性分析
2021-02-10姚高辉肖云涛
姚高辉,肖云涛
(中色卢安夏铜业有限公司 赞比亚 卢安夏 90456)
1 引言
在露天矿山开采中,露天边坡角度的大小影响着开采过程中一系列的经济技术指标[1-3]。边坡角度过小,会造成开采成本增加,影响矿山经济效益;边坡角过大,则会影响边坡稳定性,可能造成矿山人员伤亡及经济损失,影响矿山安全生产。因此,为保障露天边坡稳定性及矿山安全生产,同时降低矿山生产成本,合理确定露天边坡角度至关重要。对于露天边坡角,国内外学者做了许多研究,王东等[4]基于CDEM数值算法对边坡稳定性进行计算,对比分析了坡体位移、应力分布及演化特征,进而阐明多个弱层对复合边坡产生的叠加效应,以及清帮减载对边坡稳定性的影响。张涛江等[5]基于摩尔-库伦强度准则与折减理论,运用FLAC有限差分模拟与极限平衡分析技术,对贺斯格乌拉露天矿北排土场进行了模拟分析与研究,确定了沿基底软弱层滑动的滑坡模式。于鑫鑫等[6]依据边坡的自然地质条件、变形的基本特征,采用数值模拟和极限平衡分析相结合的理论方法,系统全面地评价了该区域的边坡稳定性,并提出了边坡稳定性的预控措施。周厚友等[7]在露天边坡的静力稳定性分析基础上,计算边坡在爆破振动下的动态响应特征,进而求得爆破荷载下边坡的位移、应力及动力安全系数等响应特征,分析边坡在爆破振动作用下的稳定状态。罗建林等[8]运用Geo-Slope及极限平衡法中的简化Bishop法、Morgenstern-Price法分别计算分析边坡3个典型剖面在天然及饱和情况下的稳定性,并提出了预防滑坡措施。
通过上述研究可知,除边坡本身的水文地质条件外,边坡稳定性分析采用的计算方法和分析软件也是研究中的重点,而在实际生产过程中,由于经济、外部环境、生产需求等因素制约,边坡往往无法达到理想状态,在设计、施工过程中的每一个环节,都可能产生边坡稳定性隐患。因此,在边坡稳定性分析和设计过程中,应采用科学的研究计算方法,综合考虑各项影响因素,才能保证边坡设计的可靠性。
本文通过采用Geo-slope软件利用极限平衡法并综合考虑矿区地震烈度对穆利亚希南一区、二区不同角度露天边坡稳定性进行计算,得出不同角度露天边坡的安全系数,分析了不同角度露天边坡稳定性,最终得到各区合理的边坡角度,为矿山露天边坡稳定性分析提供技术支撑和借鉴。
2 工程概况
赞比亚卢安夏铜矿的穆利亚希南矿区位于位于福背斜东南部的Roan-Muliashi盆地内,地层主要是加丹加超群的下罗恩(Lower Roan)群和上罗恩(Upper Roan)群沉积变质岩,基底为卢福布(Lufubu)系片岩和穆瓦(Muva)系石英岩。矿区构造主要为褶皱,基本没有断层或断层影响不大[9]。
穆利亚希南地表浅部矿体适用露天开采,其上部边坡为软岩,下部边坡为硬岩。穆利亚希南氧化矿体走向为东西方向,长约1400m,南北宽约220m,平均倾角为30°,平均厚20m,埋深1255~1125m。
3 极限平衡分析法原理
在边坡稳定性分析方法中最经典的就是极限平衡理论,在其基础上派生出了很多边坡稳定分析方法,且大都采用刚体极限平衡法[10],如图1、图2所示。
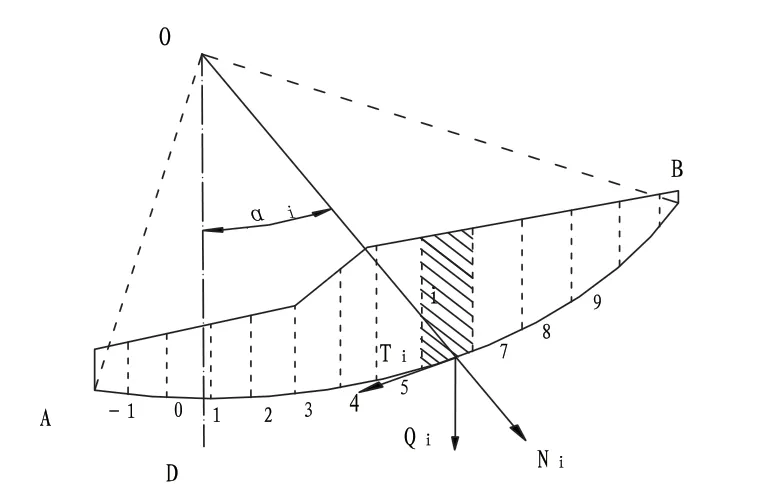
图1 边坡极限平衡分析简图
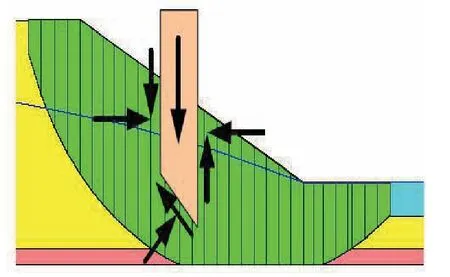
图2 条分法条带受力示意图
极限平衡法的最基本原理[11]是:
(1)假设边坡的抗剪强度服从库仑准则,其构成介质是均匀的。

其中:c为介质的粘结力,φ为介质的内摩擦角,σ为剪切面的法向应力。
(2)假设产生滑动破坏时,其产生错动的面是圆弧形,并对每一个发生滑动破坏的面进行安全系数计算,选择安全系数最小的面为最危险滑动面。
(3)将滑动体划分为许多个垂直的条块,并假设相互作用力不作用在每条块之间。
(4)根据圆弧面上水平力平衡或者力矩平衡确定(以下是力平衡):
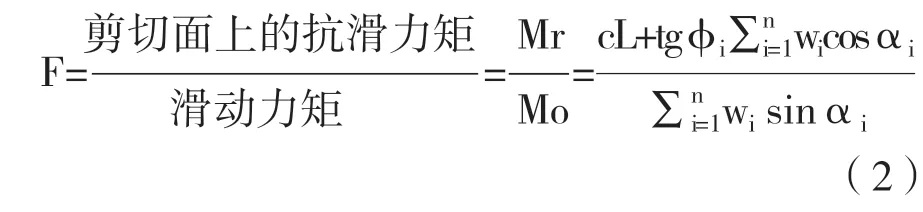
其中,L为剪切面弧长,wi为每条块重量,αi为第i条块的剪切面与水平夹角。
该方法就是得到广泛的应用的瑞典条分法,是极限平衡分析中的最基本的方法。在条块间引入相互作用力后,又发展起来了诸多分析方法,如Bishop法、Krey法、Janbu法等[12]。
4 剖面选取及岩石力学参数
本次计算主要使用Geo-slope软件,此软件中的SLOPE/W模块是专门用来分析边坡问题的模块,其在广泛应用在岩土工程界中[13-15]。
该模块主要使用有限元法并结合极限平衡理论对土木工程、地质构造、采矿工程中的边坡问题进行计算,同时也可以使用参数进行随机稳定性分析,其能有效的对孔隙水的压力状况、滑移面形状的改变、不同加载方式、土体性质等岩土工程问题进行计算。
为应用Geo-slope软件对穆利亚希南矿区边坡稳定性进行分析,需要选取典型的边坡剖面进行安全系数计算。
4.1 剖面选取
为对卢安夏穆利亚希南露采边坡进行稳定性评价,在其一区和二区共选取了10个典型计算剖面,其中一区编号分别为:P1-1、P1-2、P1-3、P1-4、P1-5,二 区 编 号 分 别 为:P2-1、P2-2、P2-3、P2-4、P2-5,如图3所示。
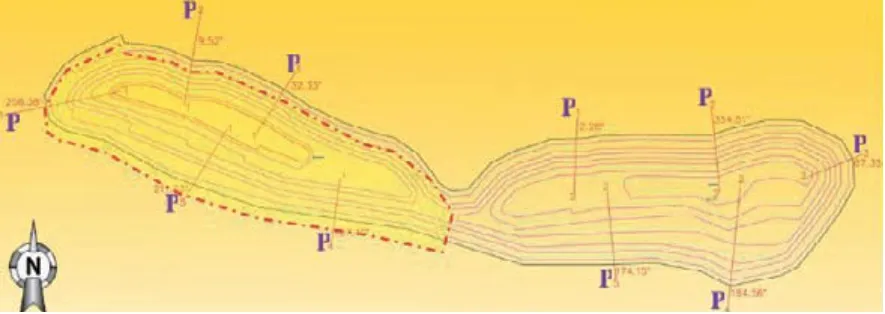
图3 露天边坡剖面选取
在Auto-CAD中处理各剖面,获取各分区不同边坡角地质剖面模型(36°、37°、38°、39°、40°和41°),为Geo-Slope极限平衡计算提供基础模型,各分区断面如图4、图5所示(由于篇幅原因,只列出了一、二分区第一个断面图)。
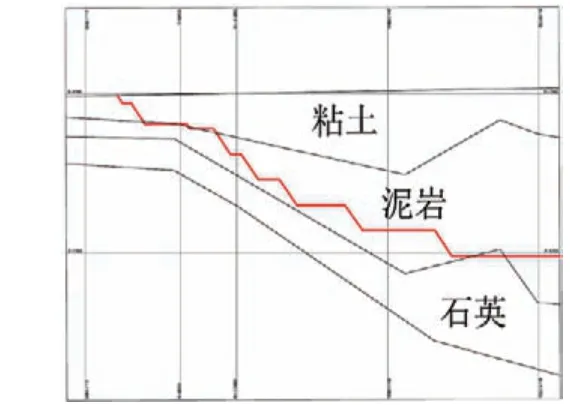
图4 P1-1断面图
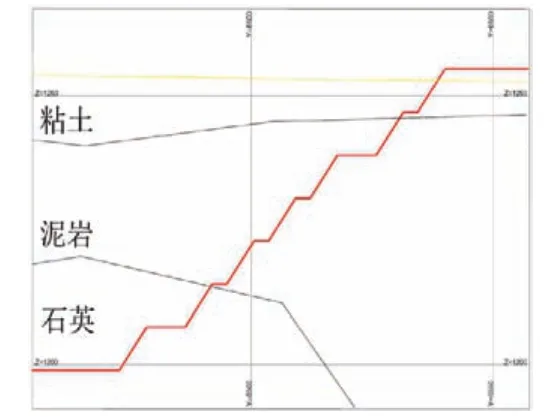
图5 P2-1断面图
4.2 岩石力学参数
在岩石力学试验结果的基础上,结合现场岩体完整性调查情况、岩石室内强度试验、饱水试验等结果,同时考虑水对岩体强度的影响,综合进行合理工程处理后得到本次计算采用的岩体强度参数[16]。如表1所示。

表1 岩体力学参数表
5 边坡稳定性计算
采用Geo-slope软件分别使用Ordinary法、Bishop法、Janbu法及Morgenstern-Price法对穆利亚希南矿区边坡不同边坡角(36°、37°、38°、39°、40°和41°)稳定性进行计算,同时在模拟计算中考虑地震对边坡稳定性的影响[17],根据拟静态方程:

式中:F为地震引起水平推力;KC为综合地震系数;W为滑体重量。
根据矿山提供的资料,穆利亚希南露天矿区历史上基本未见地震,地震设防烈度按7度考虑,地震加速度为0.1g,并结合《水工建筑物抗震设计规范》,综合地震系数计算公式为[18]:

式中:Kh为水平向地震系数,七度烈度地震区Kh为0.1; CZ为综合影响系数,一般取0.5;ai为考虑滑体重心高度的系数,一般取1.0。
根据地震危险性分析,考虑边坡的结构参数、服务年限,采用震动对边坡稳定性综合地震系数为0.05,因此卢安夏穆利亚希南矿区在地震基本烈度为VII度的工况条件下进行边坡稳定性分析。
按照规范设置边坡安全系数 最小值,在考虑地震荷载条件下取Fs=1.15。即边坡安全系数Fs计算值大于1.15,才说明边坡处于安全状态。
5.1 一区边坡稳定性分析
在考虑地震影响因素情况下,对一区边坡稳定性进行计算,各剖面安全系数计算结果如表2所示,极限平衡计算结果图如图6所示(由于篇幅原因,只列出了P1-1 Morgenstern-Price法计算结果图)。

表2 一区安全系数计算结果表
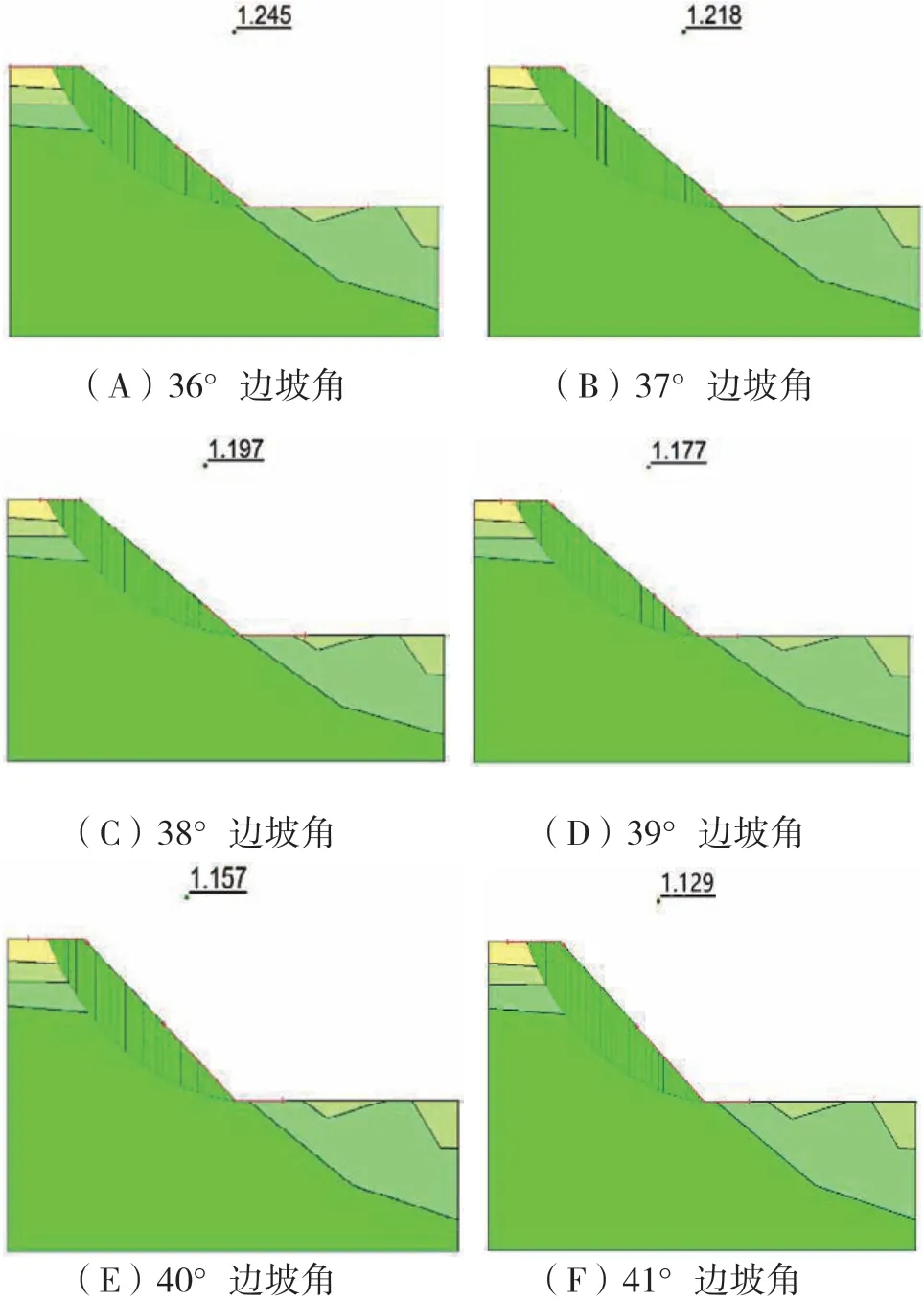
图6 剖面P1-1边坡极限平衡计算结果图
从表中可知,各方法计算结果趋势大致相同,由于瑞典圆弧法未考虑滑动土体内部的相互作用力,Janbu法忽略了条块间剪应力,假定条间合力为水平推力,但是没有满足力矩平衡条件,而Bishop法考虑了条间力的作用对瑞典法进行修正,Morgenstern-Price法给出了条间合力的作用位置,满足了力矩平衡,因此瑞典圆弧法和Janbu法计算结果偏小,Bishop法和Morgenstern-Price法计算结果偏大。综合四种计算方法的适用性和合理性,本次主要依据Morgenstern-Price法的安全系数计算结果与选定的1.15安全系数阀值进行对比,选定各分区的边坡角。
一分区在边坡角小于40°时,五个计算剖面的安全系数值均大于选定的安全系数阀值1.15,此时边坡处于稳定状态;在边坡角为41°时,五个计算断面的安全系数Fs<1.15,边坡处于欠稳定状态。因此边坡角为40°时,边坡为平衡状态,推荐一区的边坡角为40°。
5.2 二区边坡稳定性分析
参照一区边坡稳定性分析方法,确定二区边坡稳定性,各剖面安全系数计算结果如表3所示,极限平衡计算结果图如图7所示。
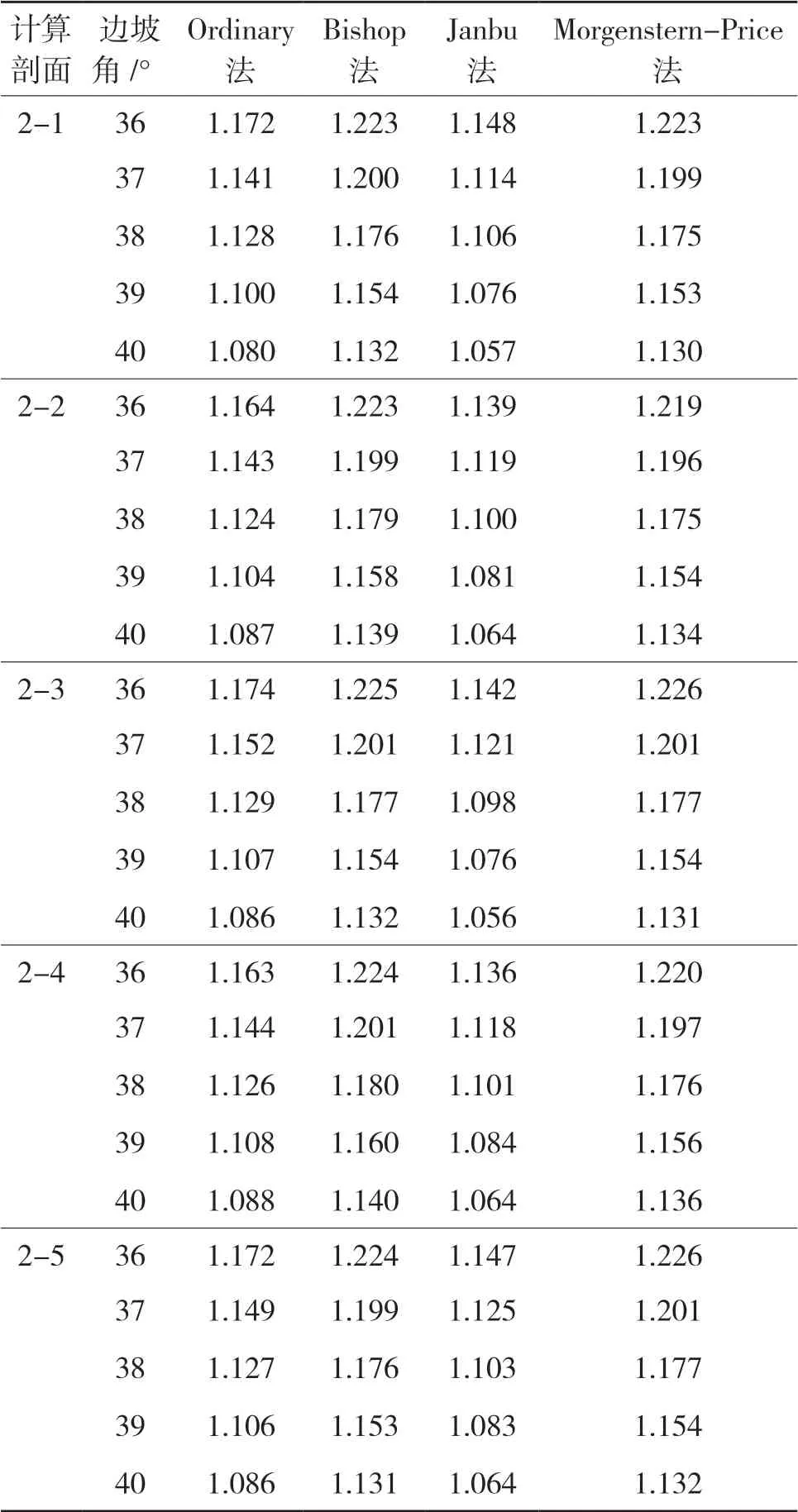
表3 二区安全系数计算结果汇总表
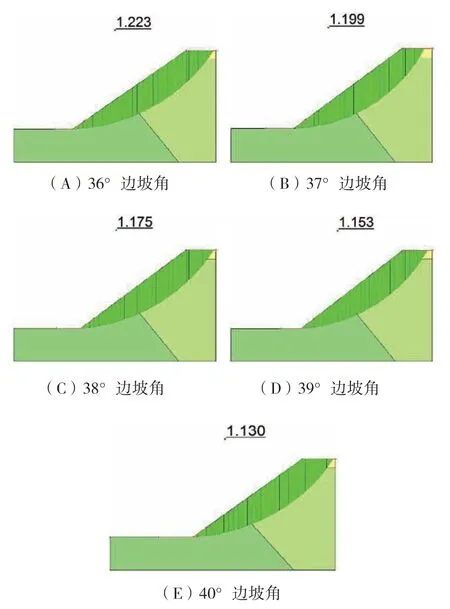
图7 剖面P2-1边坡极限平衡计算结果图
从表中可知,二区各方法计算结果趋势与一区相似,因此综合四种计算方法的适用性和合理性,本次主要依据Morgenstern-Price法的安全系数计算结果与选定的1.15安全系数阀值进行对比,选定二分区各断面的边坡角。
二分区在边坡角小于39°时,五个计算剖面的安全系数值均大于选定的安全系数阀值1.15,此时边坡处于稳定状态;在边坡角为40°时,五个计算断面的安全系数Fs<1.15,边坡处于欠稳定状态。因此边坡角为39°时,边坡为平衡状态,推荐二分区的边坡角为39°。
6 结论
由 Geo-slope软件极限平衡分析的结果可知:
(1)穆利亚希南露天矿一区最终边坡角按照40°角度设计,五个典型断面的安全系数Fs≈1.15,边坡处于最优稳定状态,该区最优边坡角推荐值为40°;
(2)穆利亚希南露天矿二区最终边坡角按照39°角度设计,五个典型断面的安全系数Fs≈1.15,边坡处于最优稳定状态,该区最优边坡角推荐值为39°。
7 建议
为保证穆利亚希南露天开采时的边坡稳定,应加强对边坡的地表观测,实时掌握边坡动态,为露天生产提供指导。
