具有非线性收获率的捕食系统的稳定性及最优收获策略

冯 倩，张 睿，李沛娟

(兰州交通大学 数理学院，甘肃 兰州 730070)

0 引言

美国生态学家Lotka[1]和意大利数学家Volterra[2]提出了Lotka-Volterra模型，其形式为

(1)

其中，x(t)为食饵的种群密度，y(t)为捕食者的种群密度，a为食饵种群的内禀增长率，b表示捕食者掠食食饵的能力，c表示食饵对捕食者的供养能力，k表示捕食者的死亡率，这里捕食者y仅以食饵x为生。作者对系统(1)进行定性分析，讨论了系统(1)平凡平衡点和正平衡点的稳定性。

1995年，李建华在系统(1)的基础上考虑了两种群的常数收获率因素，讨论了两种群都具有常数收获率的Volterra系统[3]

(2)

其中，a10表示食饵的内禀增长率，a12表示捕食者掠食食饵的能力，a21表示食饵对捕食者的供养能力，a20表示捕食者的死亡率，F和G分别表示食饵和捕食者的常数收获率。a10，a12，a20，a21均为正常数。在文献[3]中，作者讨论了系统平衡点的性质和极限环的存在性与唯一性问题。

然而，人类对食物的捕获率是不断变化的，学者们开始重视线性收获率对捕食系统的影响，并对此做出了进一步的研究[4-6]。薛春艳等[6]讨论了两种群均具有线性收获率的捕食者-食饵系统

(3)

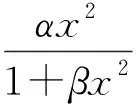
由于实际的生态系统中，人类对食物的捕获量不会随着捕获努力量和生物资源的增大而无限增大，因此，具有非线性收获率的捕食系统引起越来越多的学者关注[7-10]。薛龙跃[10]研究了带有非线性收获率的捕食系统

(4)

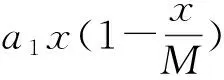
本文将文献[10]中的非线性收获率

引入模型(1)中，讨论捕食者及食饵种群均具有非线性收获率的捕食者-食饵系统

(5)

1 平衡点的存在性

鉴于其生态意义，本文只在

上对系统(5)进行讨论。通过解方程组

可得到模型(5)的平衡点:(1)平凡平衡点P1(0,0);(2)由于a>h，所以当Nbk+Nbl+hl>al时，存在正平衡点P2(x2,y2)，其中

2 平衡点的稳定性分析

系统(5)在任意平衡点(x,y)处的Jacobian矩阵为

定理1 平衡点P1(0,0)是鞍点。

证明将P1(0,0)代入J(x,y)中得到系统(5)在P1处的Jacobian矩阵为

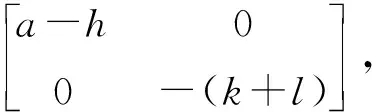
其特征方程为(λ-a+h)(λ+k+l)=0,故特征根为

λ1=a-h>0，λ2=-(k+l)<0,

所以，P1(0,0)是鞍点。

接着考虑系统(5)的正平衡点P2(x2,y2)的稳定性。将P2(x2,y2)代入J(x,y)中得到系统(5)在P2处的Jacobian矩阵为

其特征方程为

即

其中

令

则特征方程可表示为λ2-Tλ+D=0。令Δ=T2-4D,由文献[11]可知下面的结论。

定理2 (1)若D>0且Δ<0，则当T<0时，P2(x2,y2)为系统(5)稳定的焦点；当T>0时，P2(x2,y2)为系统(5)不稳定的焦点。(2)若D>0且Δ>0，则当T<0时，P2(x2,y2)为系统(5)稳定的结点；当T>0时，P2(x2,y2)为系统(5)不稳定的结点。(3)若D<0，则P2(x2,y2)为系统(5)的鞍点。

定理3 若D>0，则当T<0时，平衡点P2全局渐近稳定。

证明取Dulac函数B(x,y)=xmyn，由于

则

令

可得

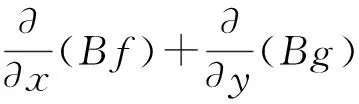
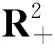
根据定理2和Dulac判据[12]得平衡点P2是全局渐近稳定的。证毕。

3 最优收获策略

根据文献[13]，运用Pontryagin最大值原理，讨论如何控制最优捕获量M和N，才能使食饵和捕食者的数量既要尽可能大的满足人类生活需求，还要让生物种群保持可持续发展。捕捞食饵和捕食者的经济收益值为

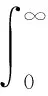
其中，b1和b2分别为食饵和捕食者种群的单价，d1和d2分别为食饵和捕食者的单位捕捞成本，ε为年折扣率。则对该系统最优收获策略的分析就转化为下面的最优控制问题。

目标函数:

其中,M和N为控制变量，0≤M≤(M)max,0≤N≤(N)max。

构建如下哈密顿函数:

其中，λ1和λ2为伴随变量，伴随方程为

根据Pontryagin最大值原理[14]，最优控制M,N要使哈密顿函数H取得最大值，则要求

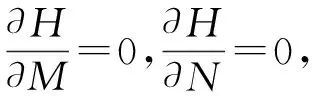
即

易得

将λ1和λ2代入伴随方程，可得

解上面方程组可得x=x*,y=y*即找到最优捕捞平衡点为(x*,y*)故最优捕获努力量为

4 结论

本文研究了一类两种群均具有非线性收获率的捕食者-食饵系统，得到了系统各平衡点局部稳定和全局稳定的充分条件，又利用Pontryagin最大值原理得到了两种群的最优收获策略，对生物资源的可持续利用有着重要意义。