供应链博弈类型与补贴行为对最优定价的影响分析
2021-02-10梁吉泰
李 延,梁吉泰
(安徽财经大学 管理科学与工程学院,安徽 蚌埠 233030)
产品价格的确定是产业链中各个环节博弈的结果。每个企业都希望赚得最多的利润,但盲目涨价的结果往往是销量下滑,利润不升反降。因此,如何寻找最优定价、获得最大利润,是人们一直想要解决的问题。要想研究供应链定价,首先应当明确供应链类型,Huang 等[1]依据供应链结构,将其分为四大类:第一类是由双制造商和单零售商组成的两层供应链[2],第二类是制造商具有线上、线下混合销售渠道的供应链[3],第三类是由两条供应链构成的双供应链[4-5],第四类是制造商同时向两个零售商提供产品的供应链[6]。本文就属于第四类中的结构,目前,此类供应链结构的研究取得了一定的进展。Fan等[7]选取了两个线上销售的零售商,发现在其中一个零售商与供应商合作的情况下,另一个零售商与平台上其他零售商横向合作能够促进原有供应链的协调,并且基本不会受平台费用差异的影响。Yang等[8]将资金约束引入供应链,发现只有当竞争强度较高时,制造商才会与其中一个零售商合并,而此时如果另一个零售商的股权融资比例高于阈值,上述合并情况会被制造商放弃。Xu等[9]考虑了绿色成本,将碳税政策纳入研究范围,并对政府减排碳税政策的制定提出具体建议。本文与上述研究存在三点不同:第一,零售商博弈方面,尽管上述研究中都存在两个零售商,但都没有考虑零售商之间的合作问题,并且部分研究没有考虑零售商之间的权利结构[9],本文则是将零售商之间的三种博弈关系都进行了完整的讨论;第二,本文对影响因素在不同水平下的作用效果通过图示进行了直观的分析;第三,本文针对零售商间的古诺博弈,提出了一种补贴策略,使博弈结果得到了有效改善,补贴双方收益增加,实现了帕累托改进。
另外,其他三类结构也同样受到了广泛的关注。Zhang等[10]发现只有当对手是单渠道销售,且自己直接销售渠道的成本低于其他渠道时,才能选择直接销售;而当对手是多渠道销售时,无论成本如何,都应当选择多渠道销售。Li等[11]在两条由单制造商和单零售商组成的供应链中分析了9种博弈模型,发现当制造商作为领导者时,零售商的跟随者劣势可以通过增加市场份额来弥补,甚至可能让制造商主动放弃领导者地位。Gu等[12]研究了在由两个制造商向零售商供应绿色补充产品的供应链中,不同互补程度下制造商是否多增加一条线上渠道的选择问题。同样,这些研究都没有在古诺博弈中考虑补贴策略行为,这也是本文与前期成果的不同之处。
在上述研究中不难发现,古诺博弈的双方较于其他博弈类型有着更低的价格和利润,这是因为古诺博弈是竞争最激烈的情况,双方通过改变价格进行竞争。因此,如果可以阻止零售商改变价格,将有效缓解竞争,提高双方的收益。要想实现这一目标,必须弥补零售商因停止改变价格而遭受的损失。首先想到的便是由政府向企业提供补贴,改变竞争环境,但由于企业数量众多、情况复杂等现实情况,政府补贴基本没有可操作性。而当我们将视角下降到两个零售商之间时,上述限制就可以得到很好地解决。因此,本文针对零售商间的古诺博弈,提出了一种补贴策略:由某一零售商主动向对方提供补贴,使其放弃改变价格,从而改善博弈结果,使双方都获得了更高的收益。
本文主要研究如下问题:一是在制造商提供存在替代性的异质产品情况下,考虑制造商领导的斯塔克尔伯格博弈中,作为跟随者的两个零售商进行三种博弈,并将其与供应链整体共谋进行对比,分析影响制造商和零售商定价决策的因素,以及因素之间的关系;二是针对零售商间的古诺博弈,提出补贴策略,并将结果与原收益进行比较,验证该策略的可行性。
1 问题描述和模型构建
在供应链中,制造商凭借自身的某些特长——资金、技术等,形成了自己为领导者、零售商为跟随者的斯塔克尔伯格博弈。零售商之间也会在利润最大化目标的驱使下,分别形成古诺、斯塔克尔伯格博弈和共谋。本文主要探讨的是单制造商作为领导者,向双零售商提供异质但有一定替代性产品的供应链中,不同的博弈模式对产品最优批发价和销售价格的影响,以及通过补贴策略改善零售商间古诺博弈结果的可行性。
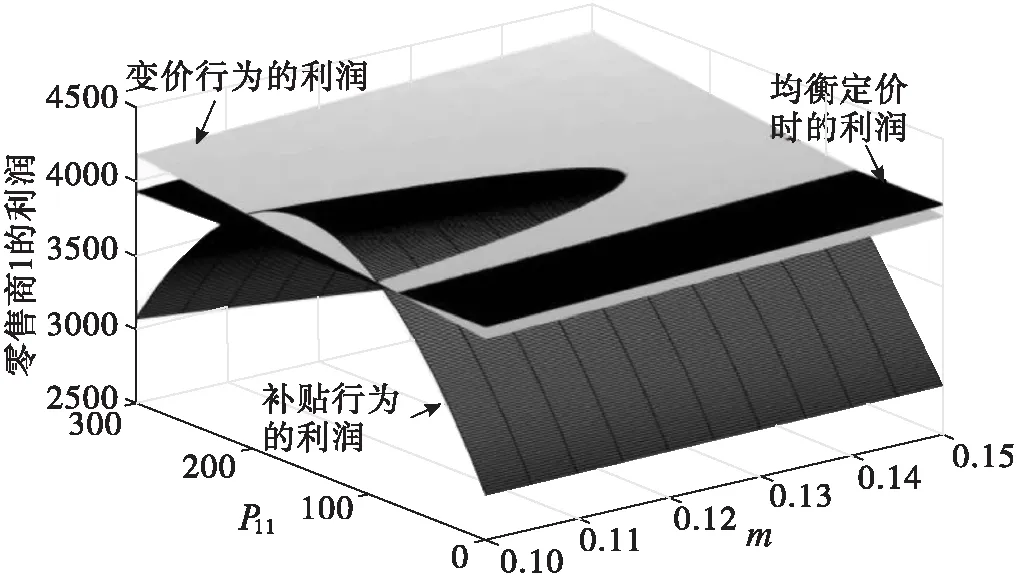
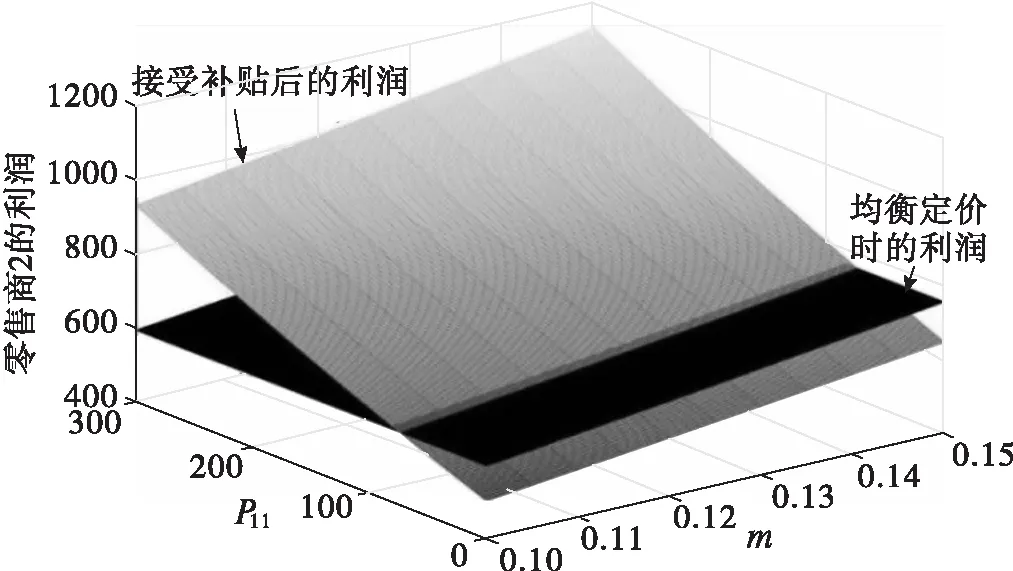
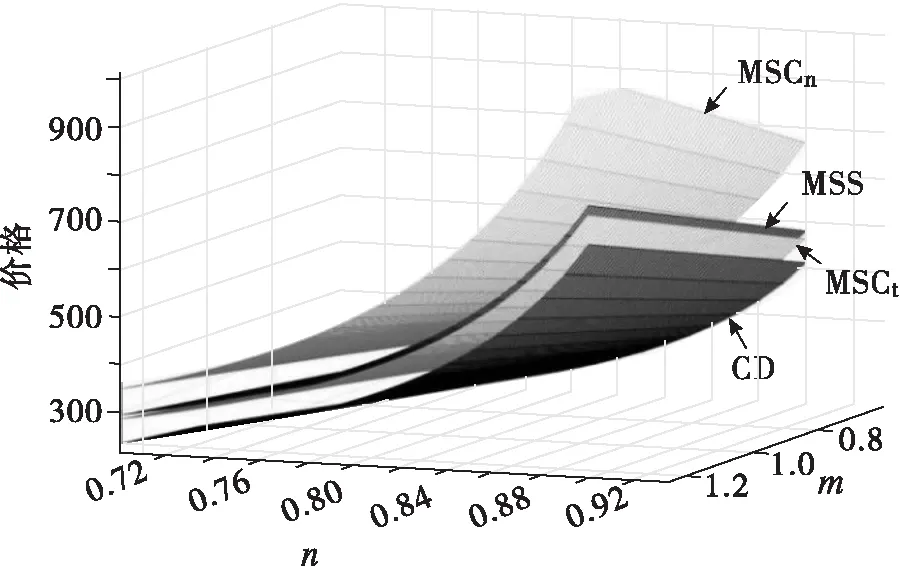
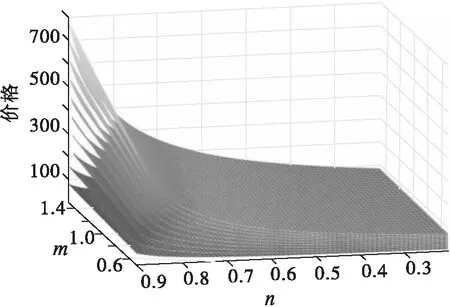
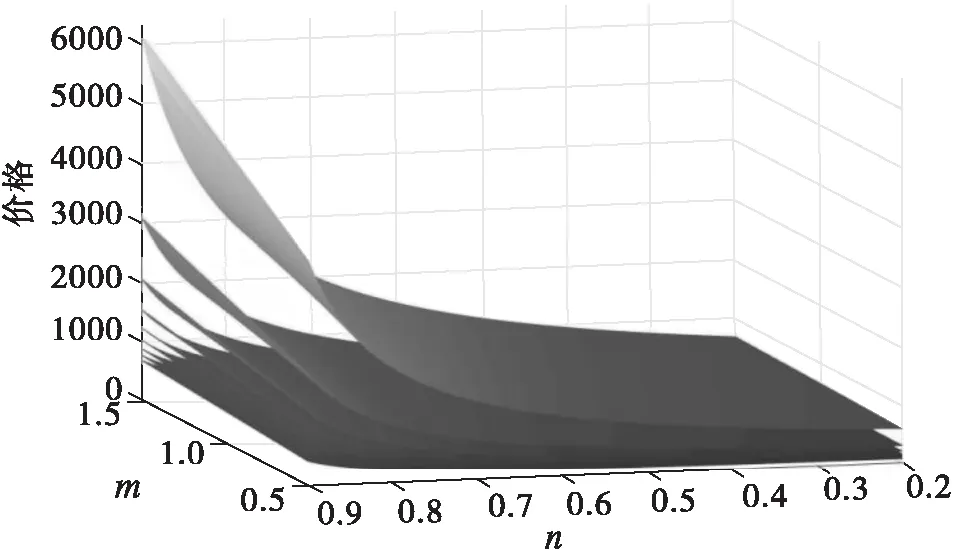
假设:两种产品的生产成本为Ci(i=1,2),制造商按批发价Wi(i=1,2)将产品分别出售给两个零售商,零售商以价格Pi(i=1,2)将产品出售给顾客;制造商和零售商都是风险中性且完全理性的决策者,都以利润最大化为目标;生产成本长期保持不变;满足不等式Ci Ds1=Q1-αP1+βP2, (1) Ds2=Q2-αP2+βP1。 (2) 其中:Ds1和Ds2分别代表零售商1和零售商2的市场需求;Qs1和Qs2分别代表产品1和产品2的潜在市场规模,该参数包含距离、服务等非价格因素导致的消费者偏好差异[1];P1和P2分别代表产品1和产品2的销售价格;α代表产品的价格弹性系数(部分文献会选择1来表示适当的价格弹性[16]);β代表产品的交叉弹性系数,且假设β<α,表示不同产品价格变动小于本产品价格变动对需求的影响。 2.1.1 无补贴行为的古诺博弈(MSCt) 建立模型如下:在制造商主导的斯塔克尔伯格博弈中,制造商为领导者,零售商为跟随者;零售商间为古诺博弈。决策顺序为:首先,在考虑零售商反应函数的基础上,制造商确定批发价Wi;然后,根据批发价Wi,两个零售商同时决定销售价格Pi。利润函数为 πs1=(P1-W1)(Q1-αP1+βP2), (3) πs2=(P2-W2)(Q2-αP2+βP1), (4) πm=(W1-C1)(Q1-αP1+βP2)+(W2-C2)(Q2-αP2+βP1)。 (5) 其中,πs1表示零售商1的利润,πs2表示零售商2的利润,πm表示制造商的利润。 根据博弈论逆序求解过程,零售商1和零售商2先分别确定P1和P2。对式(3)求关于P1的一阶导数、对式(4)求关于P2的一阶导数并令其等于零,解得 (6) (7) 再对式(3)求关于P1的二阶导数,对式(4)求关于P2的二阶导数,解得 由此可知,式(6)中的P1是关于P2的最优反应函数,式(7)中的P2是关于P1的最优反应函数,如图1所示。 图1 古诺均衡 联立式(6)(7),解得 (8) (9) 其中,PMSCt1和PMSCt2分别表示在零售商作为跟随者的斯塔克尔伯格博弈中,零售商1与零售商2间古诺博弈确定的销售价格关于批发价的反应函数。 注 对式(3)(4)求得黑塞矩阵,并且验证该黑塞矩阵为正定,因此式(8)(9)中的PMSCt1和PMSCt2并不能实现利润最大化,而是经过古诺博弈实现的均衡解。 将PMSCt1和PMSCt2代入式(5),得到制造商的利润函数 (10) 对式(10)关于W1和W2分别求一阶偏导数,并令其等于零,解得 再根据式(10),得到πm关于W1和W2的黑塞矩阵 (11) 2.1.2 通过补贴行为优化的古诺博弈 古诺博弈是:假设对方价格不会因自己的定价发生改变,确定关于对方价格的反应函数,最后形成均衡价格。流程如下: 步0 零售商1给出初始定价P11。 步1 零售商2确定此时的最优价格P21,此时零售商2的利润为π21。 步2 零售商1根据零售商2的定价确定自己的最优价格P12。此时,零售商1的利润为π11,零售商2的利润为π22。 步3 零售商2根据零售商1的定价确定自己的最优价格P22,此时零售商2的利润为π23。 步4 零售商1根据零售商2的定价确定自己的最优价格P13,此时零售商1的利润为π12。 最终结果为零售商1、零售商2分别确定各自的均衡定价。 由上述步骤可以发现,如果零售商1在步2确定最优价格P12后,给予零售商2足够的补贴(即零售商2通过调整价格可以增加的利润),就能使零售商2放弃将价格从P21调整到P22,博弈也就能在达到均衡价格之前中止。而要想通过补贴中止博弈,就需要满足两个条件: (1)π11>π23-π22,该条件要求零售商1的利润能够超过零售商2变价行为带来的利润增长额,保证零售商1有足够的利润实施补贴; (2)π11-(π23-π22)>π12,该条件要求零售商1实施补贴后的剩余利润能够超过自己采取变价行为带来的利润,保证零售商1有足够的动力实施补贴。 零售商1在满足了这两个条件后采取补贴行为,零售商2则会因为得到了足够的补贴,同意保持一个处于劣势的价格。最后将实施补贴行为后的利润与古诺博弈达到均衡后的利润进行比较,判断补贴行为对利润的提升效果。 假设零售商1的初始定价为P11,根据式(3)~(7),得 即步1中零售商2的最优定价P21和利润π21。进一步可得 即步2中,零售商1的最优定价P12,以及零售商2还未改变价格时零售商1的利润π11和零售商2的利润π22。继而可得 即步3中,零售商2将价格改为P22,此时利润为π23。最后可得 即步4中,零售商1将价格改为P13,此时利润为π12。 由图2可以发现:首先,零售商1采取补贴行为时利润大于零,说明有足够的利润支持补贴行为;其次,零售商1初始定价在(100,200)以内、零售商2占零售商1市场份额的13%以内时,采取补贴行为可以获得比自己改变价格更高的利润,说明有足够的动力采取补贴行为;最后,在补贴行为更优区域内,采取补贴行为的利润高于均衡定价的利润。根据图3,在补贴行为更优区域内,零售商2接受补贴的利润高于均衡定价的利润。 图2 零售商1的利润 图3 零售商2的利润 综上,在古诺博弈过程中存在一个合理区域,让市场份额占比非常高的一方有足够的能力和动力采取补贴行为,阻止对方改变价格,让古诺博弈在达到均衡价格之前中止,使两个零售商1都获得比均衡状态更高的利润,实现双赢。 建立模型如下:在制造商主导的斯塔克尔伯格博弈中,制造商为领导者,零售商为跟随者;在零售商之间的斯塔克尔伯格博弈中,零售商1为领导者,零售商2为跟随者(零售商1与零售商2领导权互换后的情况与该模型完全一致,不再讨论)。决策顺序为:首先,在考虑零售商反应函数的基础上,制造商确定批发价Wi;然后,根据批发价和零售商2的反应函数,零售商1确定产品1的销售价格P1;最后,零售商2确定产品2的销售价格P2。 根据博弈论逆序求解过程,先确定产品2的销售价格P2。 将式(7)中的P2代入式(3),再对P1求一阶导数并令其等于零,解得 (12) 再对P1求二阶导数,解得 (13) 由式(13)可知,式(12)中的是PMSS1极大值点。将PMSS1代入式(7),解得 (14) 其中:PMSS1表示在制造商领导的斯塔克尔伯格博弈中,零售商1作为零售商间斯塔克尔伯格博弈的领导者时价格关于批发价的反应函数;PMSS2表示零售商2作为零售商间斯塔克尔伯格博弈的跟随者时价格关于批发价的反应函数。 将PMSS1和PMSS2代入式(5),得到制造商的利润函数 (15) 对式(15)关于W1和W2分别求一阶偏导数,并令其等于零,解得 再根据式(15),得到πm关于W1和W2的黑塞矩阵 (16) 建立模型如下:在制造商占主导的斯塔克尔伯格博弈中,制造商为领导者,零售商为跟随者;零售商间采取合作。决策顺序为:首先在考虑零售商反应函数的基础上,制造商确定批发价Wi;然后根据批发价,两个零售商以零售商利润之和最大化为目标,共同制定产品1和产品2的销售价格P1、P2。零售商利润之和函数为 πs=(P1-W1)(Q1-αP1+βP2)+(P2-W2)(Q2-αP2+βP1), (17) 其中,πs表示在制造商占主导的斯塔克尔伯格博弈中,零售商间采取合作时,零售商的利润之和。 根据博弈论逆序求解过程,零售商1和零售商2先确定销售价格P1和P2。对式(17)中的P1和P2分别求一阶偏导数,并令其等于零,解得 (18) (19) 再根据式(17)得到πs关于P1和P2的黑塞矩阵 (20) 根据舒尔补引理及β<α,式(20)表示的黑塞矩阵是负定的,因此PMSCn1和PMSCn2是极大值点,分别表示在制造商领导的斯塔克尔伯格博弈中,零售商采取合作时,产品1、2的销售价格关于批发价的反应函数。 将PMSCn1和PMSCn2代入式(5),得到制造商利润为 (21) 对W1和W2分别求一阶偏导数,并令其等于零,解得 再根据式(21)可得πm关于W1和W2的黑塞矩阵 (22) 建立模型如下:制造商与两个零售商共谋,共同制定销售价格P1和P2,实现供应链整体利润最大化。利润函数为 πC=(P1-C1)(Q1-αP1+βP2)+(P2-C2)(Q2-αP2+βP1), (23) 其中,πC表示在制造商与零售商们采取共谋时,供应链利润之和。 对P1和P2分别求一阶偏导数,并令其等于零,解得 再根据式(23)得到πC关于P1和P2的黑塞矩阵 (24) 由于本文中零售商1和零售商2的选择无特殊性,因此以下结论同时适用于产品1和产品2。通过对上述计算结果进行分析,可以得到以下结论。 (Ⅰ)对上述不同情况下的最优均衡价格进行比较,可以得到 该式表明,在制造商占领导地位时,无论零售商间采取何种博弈,都不会影响最优批发价;当制造商与零售商的博弈由共谋变为制造商领导的斯塔克尔伯格博弈时,批发价正好与共谋时的销售价格相等。不难发现,供应链整体的共谋行为会产生最低的销售价格,这也科学地解释了在实际市场中,能够整合产业链上下游的企业可以提供最有竞争力的售价。 图4 r和m对产品1最优定价的影响 图5 n和m对产品1最优定价的影响 图6 不同市场规模下m和n对最优定价的影响 图7 不同价格弹性下m和n对最优定价的影响 由图7可以得出:随着价格弹性的降低,价格可替代性对最优销售价格上涨的促进作用会增强。当价格弹性降低时,价格可替代性的增强意味着两种产品有着更加接近的替代水平,消费者因价格变化的流动会更加剧烈,直觉上的判断和现实情况更多的是两家零售商都会降价促销。这就出现了理论与实际相互矛盾的情况,但并非是模型或计算错误,而是零售商长期目标与短期目标的冲突。本文中的利润最大化是长期目标,但在现实中,企业可能会面临现金流短缺、市场剧烈波动、竞争企业技术突破等短期挑战。例如,2020年受新冠疫情影响,Adidas、Nike等快消品牌的营收大幅降低,库存积压一度达到数年销售之和,不得不选择降价促销来回笼资金,保证企业的存续。 在由单制造商和双零售商组成的供应链中,三者采取共谋行为时销售价格最低;在制造商领导下的斯塔克尔伯格博弈中,无论零售商间采取何种博弈模式,最优批发价都不会改变,并且此时的批发价正好与三者共谋时的销售价格相等。当零售商间采取古诺博弈时,存在一个合理区域,让市场份额遥遥领先的一方采取补贴行为,中止博弈进程,并且让零售商双方都获得利润的增长。存在一个反直觉的结论:市场份额的增加反而会导致价格提升。在不同博弈模型的对比中发现,对价格提升产生作用的因素从大到小的顺序为:价格可替代性的增加、潜在市场规模差异的增加、成本差异的增加。并且,价格弹性的降低、潜在市场规模的增加,会导致价格可替代性和市场规模差异的变化对价格的提升作用更加显著。 由此可知,在产品的经营中,应尽可能地保证产品具有较低的价格弹性和较大的潜在市场规模。首先应通过对买前推荐、售后服务等非价格因素的关注和投入,拉大与竞品的市场规模差异;其次,通过广告宣传,将产品提升为生活必需品,降低价格弹性;最后,在通过上述两种策略实现占优的市场份额后,主动采取补贴行为,避免过度竞争。2 制造商主导的斯塔克尔伯格博弈(MS)
2.1 零售商间古诺博弈
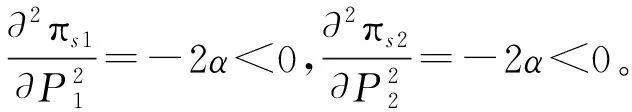


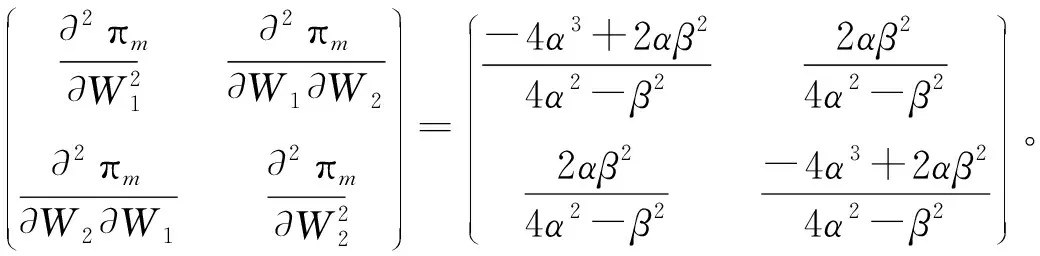

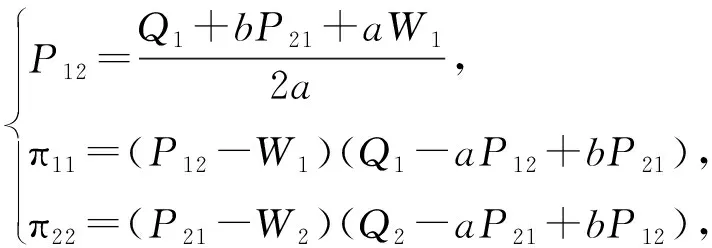
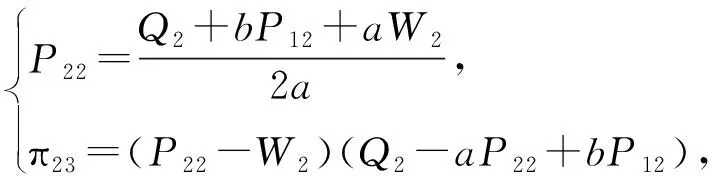

2.2 零售商间斯塔克尔伯格博弈(MSS)
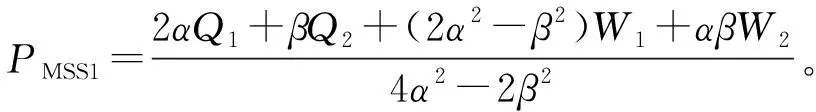

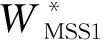
2.3 零售商间共谋(MSCn)

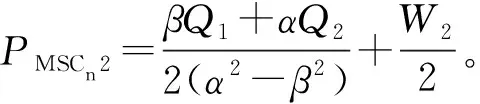
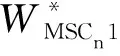
3 制造商与零售商们共谋(CD)

4 实例分析
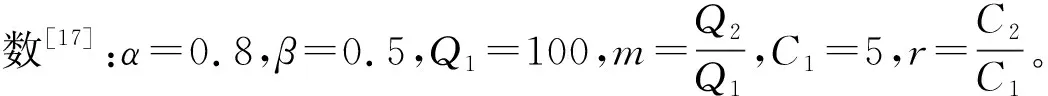

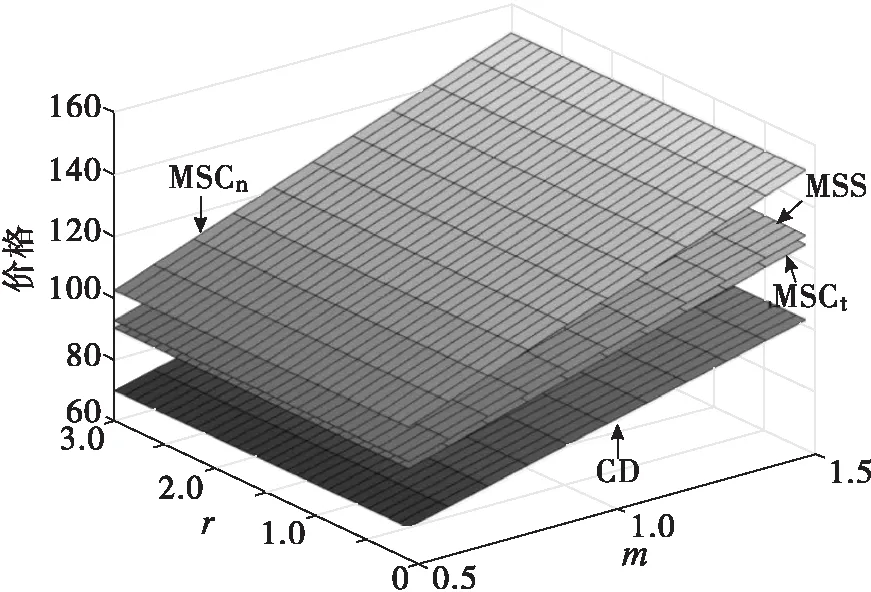


5 总结
