基于不同归一化参数的单自由度体系残余位移比离散性研究
2021-02-09胡进军刘巴黎
胡进军 刘巴黎
摘要:结构弹塑性特征的差异会引起残余位移较大的离散性,使得强震下结构残余位移难以准确预测.为准确评估和预测震后结构残余位移,实现精细化的抗震设计和评估,有必要研究结构残余位移的离散性.鉴于此,基于大量分类地震动记录,选用不同的归一化参数分别定义残余位移比,通过非线性时程分析建立单自由度体系残余位移比谱,研究弹塑性特征参数(延性系数和强度折減系数)以及场地条件对残余位移比离散性的影响,建立了残余位移比变异系数谱的拟合公式.结果表明:残余位移与弹塑性谱位移的相关性比与弹性谱位移更好;结构残余位移比离散性受场地类别的影响较小;残余位移比变异系数谱分别随延性系数和强度折减系数的增大而增大;选择弹塑性谱位移作为归一化参数可以减小结构残余位移比离散性.
关键词:残余位移;归一化参数;相关性;离散性;结构弹塑性特征参数
中图分类号:P315.92文献标志码:A
基金项目:国家自然科学基金重点项目(U1939210),National Natural Science Foundation of China(U1939210)
Study on Variability of Residual Displacement Ratios Based on Different Normalized Parameters for SDOF Systems
HU Jinjun1,2,LIU Bali1,2
(1. Institute of Engineering Mechanics,China Earthquake Administration,Harbin 150080,China;2. Key Laboratory of Earthquake Engineering and Engineering Vibration,China Earthquake Administration,Harbin 150080,China)
Abstract:The elastic-plastic characteristics of the structure will lead to large dispersion of the residual dis-placements,which makes it difficult to predict the residual displacements accurately under strong earthquake excita-tions. In order to accurately evaluate and predict the residual displacements of the structure and realize the refined a-seismic design,it is necessary to investigate the dispersion of the residual displacement of structures. In the light of this,based on a large number of classified ground motions,different normalized parameters are used to define the residual displacement ratio in this paper. The residual displacement ratios spectra of single degree of freedom(SDOF)systems are constructed by means of nonlinear response time-history analyses. The results are statistically organized to evaluate the influence of the following parameters: elastic-plastic characteristic parameters(ductility factor and strength reduction factor)and site condition. A simplified expression is presented to estimate the variation coefficient spectra of residual displacement ratios. It is concluded that the correlation between residual displacements and inelas-tic spectral displacements is better than that between residual displacements and elastic spectral displacements. The dispersion of the residual displacements is less affected by the site conditions. The variation coefficient spectra of residual displacement ratios increase with the increase of elastic-plastic characteristic parameters. It is suggested to select the inelastic spectral displacement as the normalized parameter,which can reduce the dispersion of the residual displacement ratios.
Key words:residual displacement;normalized parameter;correlation;dispersion;elastic-plastic characteristic parameter of structure
结构在强震作用下进入非线性阶段会产生不可恢复的残余位移[1],结構残余位移是抗震性能评估和地震损失评估的重要参数[2-5]. FEMA P-58[6]将残余位移作为决定结构震后修复或拆除的重要指标.《建筑抗震韧性评价标准》(GB/T 38591—2020)[7]中建筑的抗震韧性由弹塑性时程分析的层残余变形结合其限值确定,并给出了部分结构形式层残余位移角的限值.
结构自身弹塑性特征的不同会引起地震响应较大的离散性,使得强震下结构性态难以准确预测[8]. Kawashima等[9]对双线性单自由度(SDOF)体系的残余位移进行研究,认为屈服后刚度对残余位移谱离散性影响较大,场地条件、延性系数和自振周期对残余位移谱离散性影响较小. Ruiz-Garcia和Miranda[10]对SDOF体系采用弹性谱位移归一化的残余位移比谱进行了系统研究,结果表明强度折减系数对残余位移比谱离散性影响较小,自振周期对残余位移比谱离散性影响较大.胡晓斌和贺慧高[11]采用不同的参数对残余位移进行归一化,对双线性SDOF体系残余位移离散性进行了研究,结果表明自振周期与屈服后刚度对残余位移离散性有影响,强度折减系数对残余位移比谱离散性影响较小. Harikrishnan和Gupta[12]采用弹塑性谱位移和弹性谱位移对残余位移进行归一化,对理想弹塑性(EPP)SDOF体系残余位移比离散性进行了研究,认为延性系数和自振周期对残余位移比离散性有一定的影响,地震动持时对残余位移比离散性影响很小. Harikrishnan和Gupta[13]对SDOF体系等强度残余位移比谱进行了进一步研究,结果表明强度折减系数和自振周期对残余位移比离散性有一定的影响.
综上所述,结构弹塑性特征参数(屈服后刚度、延性系数和强度折减系数等)和地震动的随机性对结构残余位移离散性影响的诸多结论不一致.总体而言,与地震作用下结构最大位移响应的离散性相比,结构残余位移响应离散性更大[10].弹塑性特征以及地震动的复杂性和随机性所导致的结构残余位移响应的较大离散性,不仅使得结构残余位移难以准确预测和评估,也成为结构抗震性态评估以及基于性能的抗震设计发展的困难.本文旨在对残余位移的离散性进行系统的研究,从减小结构残余位移比离散性的角度,分析了不同归一化参数对等延性和等强度残余位移比谱离散性的影响,并给出了残余位移比谱离散性较小的归一化参数,同时构建了等延性和等强度残余位移比变异系数谱的拟合公式,为准确预测和评估结构残余位移,实现精细化的抗震设计和评估提供参考.
1数据来源
本文所选地震动来源于美国太平洋地震工程研究中心(PEER NGA-West2)强震数据库,挑选原则[14]如下:1)矩震级大于5.7;2)地震动峰值加速度(PGA)大于40 cm/s2;3)不包含脉冲型地震动.据此,本文挑选了全球范围内的280条地震动记录,依据NEHRP[15]规范的场地划分标准分为四类,AB类(A类和B类合为一类)、C类、D类及E类,每类场地选取了70条地震动记录.地震动的震级-断层距分布如图1所示.

2残余位移比的定义
研究结构震后残余位移ur时,国内外学者通常将ur进行归一化得到无量纲的残余位移,即残余位移比Cr.常用的归一化参数包括屈服位移uy、最大可能残余位移ur,m、弹塑性谱位移sdi以及弹性谱位移sde.
uy是最早被采用的归一化参数,Mahin和Bert-ero[16]通过对EPP模型的SDOF体系等延性弹塑性谱进行研究,并且采用屈服位移对残余位移归一化,研究表明结构残余位移可能超过最大弹塑性位移的40%.胡晓斌和贺慧高[11]与Farrow和Kurama[17-18]也采用屈服位移对残余位移进行归一化研究.
ur,m即结构从最大位移点卸载后剩余的不可恢复的变形. Macrae和Kawashima[19]采用最大可能残余位移对残余位移进行归一化,首次对双线性SDOF性体系的残余位移进行了系统详细的研究. Kawashima等[9]采用最大可能残余位移对残余位移进行归一化,进一步研究了屈服后刚度、延性系数、震级、震中距及场地类别对双线性SDOF体系残余位移比谱的影响.
sdi(Borzi等[20];Christopoulos等[21];Harikrishnan和Gupta[12-13])以及sde(Ruiz-Garcia和Miranda[10];Ji等[22])为最常用的归一化参数.本文分别采用sdi和sde对残余位移进行归一化,定义结构残余位移比Cr.相关参数如图2所示.
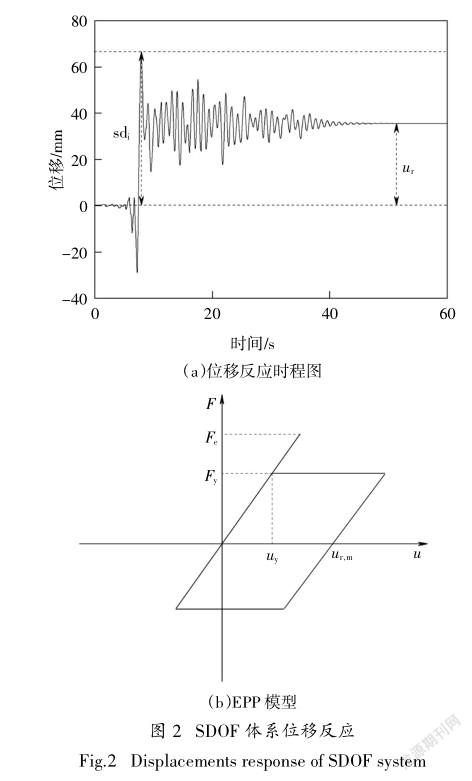
3残余位移与归一化参数相关性分析


周期小于0.5 s时,不同μ的残余位移与归一化参数(sdi和sde)的相关系数随周期增大而增幅较大.周期大于0.5 s时,不同μ的残余位移与归一化参数的相关系数随周期增大而增幅较小.

周期小于0.5 s时,不同α的残余位移与归一化参数的相关系数随周期增大而减小;周期大于0.5 s时,不同α的残余位移与归一化参数的相关系数随周期增大而增大;存在临界周期值(0.5 s),大于或小于临界周期值时,不同α的残余位移与归一化参数之间的相关性趋势发生很大变化,这一点与文献[24]的结论一致.
总体而言,残余位移与归一化参数的相关系数受弹塑性特征参数(μ和α)的影响较小.残余位移与sdi的相关性较大,与sde的相关性较小.这是因为sdi包含自振周期、阻尼以及反映结构弹塑性特征的参数(延性系数)等信息,而sde中没有包含反映结构弹塑性特征的参数信息.
4残余位移比谱离散性分析
地震动本身具有极强的随机性,不同的地震动计算结果差距可能高达数倍[25],结构弹塑性特征也会引起地震响应较大的离散性[8],相关研究中各因素对残余位移离散性影响的结论也不一致.本文采用变异系数(COV)来描述和评价残余位移比的离散性,研究延性系数、强度折减系数和场地类别对残余位移比离散性的影响.
4.1场地条件的影响
按照场地分类AB、C、D和E类,计算μ为2的各类场地不同归一化参数的等延性残余位移比COV谱,结果如图5(a)和(b)所示.α为2的各类场地不同归一化参数的等强度残余位移比COV谱,结果如图5(c)和(d)所示.可以看出:四类场地等延性和等强度残余位移比COV谱差距较小,说明结构残余位移的离散性受场地类别的影响较小;结构自振周期小于0.5 s时,等延性和等强度残余位移比COV谱随着周期增大而减小;结构自振周期大于0.5 s时,等延性和等强度残余位移比COV谱趋于不变,即周期大于0.5 s时等延性和等强度残余位移比COV谱对周期变化不敏感.
4.2延性系数的影响
延性系数μ为结构最大位移和屈服位移之比.分别取μ为2、3、4、5和6,计算四类场地平均等延性残余位移比COV谱,结果如图6所示.可以看出:等延性残余位移比COV谱分别随延性系数的增大而增大.等延性残余位移比离散性受归一化参数的影响较为显著,与sde作为归一化参数的残余位移比COV相比,sdi作为归一化参数的等延性残余位移比COV更小.这是因为残余位移与sdi的相关性较大,与sde的相关性较小,选择与残余位移相关性较大的参数(sdi)对其归一化后得到的等延性残余位移比COV更小.结构自振周期小于0.5 s时,等延性残余位移比COV随着周期增大而减小;结构自振周期大于0.5 s时,等延性残余位移比COV趋于不变,即周期大于0.5 s时等延性残余位移比COV谱对周期变化不敏感.


4.3强度折减系数的影响
强度折减系数α为结构保持弹性所需的最小强度与屈服强度之比.分别取α为2、3、4、5和6,计算四类场地平均等强度残余位移比COV谱,结果如图7所示.可以看出:等强度残余位移比COV谱分别随强度折减系数的增大而增大.等强度残余位移比离散性受归一化参数的影响较为显著,与sde作为归一化参数的残余位移比COV相比,sdi作为归一化参数的等强度残余位移比COV更小.这是因为选择与残余位移相关性较大的参数(sdi)对其归一化后得到的等强度残余位移比COV更小.结构自振周期小于0.5 s时,等强度残余位移比COV随着周期增大而减小;结构自振周期大于0.5 s时,等强度残余位移比COV趋于不变,即周期大于0.5 s时等强度残余位移比COV谱对周期变化不敏感.
5残余位移比变异系数谱拟合


6结论
本文分析SDOF体系残余位移与归一化参数(弹塑性谱位移、弹性位移)的相关性,基于大量地震动记录建立了等延性和等強度残余位移比变异系数谱,分析了延性系数、强度折减系数和场地类别对残余位移比谱离散性的影响.主要结论如下:
总体而言,残余位移与弹塑性谱位移的相关性较大,与弹性谱位移的相关性较小.这是因为弹性谱位移包含自振周期、阻尼以及反映结构弹塑性特征的参数(延性系数)等信息,而弹性谱位移中没有包含反映结构弹塑性特征的参数信息.残余位移与归一化参数的相关性受延性系数和强度折减系数的影响较小.
等延性和等强度残余位移比离散性受场地类别的影响较小.残余位移比变异系数谱分别随延性系数和强度折减系数的增大而增大.结构自振周期小于0.5 s时,残余位移比变异系数谱随着周期增大而减小;结构自振周期大于0.5 s时,残余位移比变异系数谱趋于不变.
等延性和等强度残余位移比离散性受归一化参数的影响较为显著.与弹性谱位移相比,弹塑性谱位移作为归一化参数得到的残余位移比变异系数更小.因此,选择弹塑性谱位移作为归一化参数可以减小结构残余位移比离散性.
致谢:感谢美国太平洋地震工程研究中心(PEER)NGA计划项目提供的地震动数据!
参考文献
[1]PAMPANIN S,CHRISTOPOULOS C,NIGEL PRIESTLEY M J. Performance-based seismic response of frame structures including residual deformations. part ii:multi-degree of freedom systems[J]. Journal of Earthquake Engineering,2003,7(1):119—147.
[2]YAZGAN U,DAZIO A. The use of post-earthquake residual dis-placements as a performance indicator in seismic assessment[J]. Georisk:Assessment and Management of Risk for Engineered Sys-tems and Geohazards,2011,5(1):59—76.
[3]YAZGAN U,DAZIO A. Post-earthquake damage assessment using residual displacements[J]. Earthquake Engineering & Structural Dynamics,2012,41(8):1257—1276.
[4]RAMIREZ C M,MIRANDA E. Significance of residual drifts in building earthquake loss estimation[J]. Earthquake Engineering & Structural Dynamics,2012,41(11):1477—1493.
[5]RUIZ-GARCIA J,AGUILAR J D. Aftershock seismic assessment taking into account postmainshock residual drifts[J]. Earthquake Engineering & Structural Dynamics,2015,44(9):1391—1407.
[6]FEMA. Seismic performance assessment of buildings,Volume 1,methodology[R]. Washington DC:Federal Emergency Management Agency,2012:130—139.
[7]建筑抗震韌性评价标准:GB/T 38591—2020[S].北京:中国标准出版社,2020. Standard for seismic resilience assessment of buildings:GB/T 38591—2020[S]. Beijing:Standards Press of China,2020.(In Chinese)
[8]叶列平,陆新征,马千里,等.屈服后刚度对建筑结构地震响应影响的研究[J].建筑结构学报,2009,30(2):17—29. YE L P,LU X Z,MA Q L,et al. Influence of post-yielding stiffness to seismic response of building structures[J]. Journal of Building Structures,2009,30(2):17—29.(In Chinese)
[9]KAWASHIMA K,MACRAE G A,HOSHIKUMA J I,et al. Residual displacement response spectrum[J]. Journal of Structural Engineer-ing,1998,124(5):523—530.
[10]RUIZ-GARCIA J,MIRANDA E. Residual displacement ratios for assessment of existing structures[J]. Earthquake Engineering & Structural Dynamics,2006,35(3):315—336.
[11]胡晓斌,贺慧高.等强残余位移系数谱研究[J].工程力学,2015,32(1):163—167.HU X B,HE H G. Study on equal-strength residual displacement ratio spectrum[J]. Engineering Mechanics,2015,32(1):163—167.(In Chinese)
[12]HARIKRISHNAN M G,GUPTA V K. Scaling of constant-ductility residual displacement spectrum[J]. Earthquake Engineering & Structural Dynamics,2020,49(3):215—233.
[13]HARIKRISHNAN M G,GUPTA V K. Scaling of residual displace-ments in terms of elastic and inelastic spectral displacements for ex-isting SDOF systems[J]. Earthquake Engineering and Engineering Vibration,2020,19(1):71—85.
[14]MIRANDA E. Inelastic displacement ratios for structures on firm sites[J]. Journal of Structural Engineering,2000,126(10):1150—1159.
[15]FEMA. NEHRP recommended provisions for seismic regulations for new buildings and other structures[R]. Washington DC:Building Seismic Safety Council,2003:17—30.
[16]MAHIN S A,BERTERO V V. An evaluation of inelastic seismic de-sign spectra[J]. Journal of the Structural Division,1981,107(9):1777—1795.
[17]FARROW K T,KURAMA Y C. SDOF demand index relationships for performance-based seismic design[J]. Earthquake Spectra,2003,19(4):799—838.
[18]FARROW K T,KURAMA Y C. SDOF demand index relationships for performance-based seismic design[J]. Earthquake Spectra,2003,19(4):799—838.
[19]MACRAE G A,KAWASHIMA K. Post-earthquake residual dis-placements of bilinear oscillators[J]. Earthquake Engineering & Structural Dynamics,1997,26(7):701—716.
[20]BORZI B,CALVI G M,ELNASHAI A S,et al. Inelastic spectra for displacement-based seismic design[J]. Soil Dynamics and Earth-quake Engineering,2001,21(1):47—61.
[21]CHRISTOPOULOS C,PAMPANIN S,NIGEL PRIESTLEY M J. Performance-based seismic response of frame structures including residual deformations. part i:single-degree of freedom systems[J]. Journal of Earthquake Engineering,2003,7(1):97—118.
[22]JI D F,WEN W P,ZHAI C H,et al. Residual displacement ratios of SDOF systems subjected to ground motions recorded on soft soils[J]. Soil Dynamics and Earthquake Engineering,2018,115:331—335.
[23]YAZGAN U,DAZIO A. Simulating maximum and residual displace-ments of RC structures:II.sensitivity[J]. Earthquake Spectra,2011,27(4):1203—1218.
[24]郝建兵,吳刚,吴智深. SDOF体系残余变形响应与地震强度指标相关性分析[J].土木工程学报,2013,46(6):1—7. HAO J B,WU G,WU Z S. Correlation analysis between residual de-formation of SDOF system and ground motion intensity indices[J]. China Civil Engineering Journal,2013,46(6):1—7.(In Chinese)
[25]张耀庭,刘勇,沈杰,等.结构动力时程分析的地震动选择方法研究[J].湖南大学学报(自然科学版),2020,47(7):29—39. ZHANG Y T,LIU Y,SHEN J,et al. Research on ground motion se-lection method for time-history analysis of structure[J]. Journal of Hunan University(Natural Sciences),2020,47(7):29—39.(In Chinese)
[26]MILLIKEN G A. Nonlinear regression analysis and its applications[J]. Technometrics,1990,32(2):219—220.
