谱好学生提问三部曲 奏响数学课堂最强音

胡军 朱丽霞

摘    要：学生提问是学生主体地位的重要体现，也是培养学生问题意识和创新思维的有效途径.在数学课堂中，培养学生提出问题的能力，需要谱好三部曲，即“敢问曲”“善问曲”和“乐问曲”.

关键词：数学教学;提问能力;三部曲

如何从教师设计问题走向教师引导学生发现和提出问题，不断提升学生发现和提出高层次问题的能力，最终形成学生乐于提出问题的探究状态，成为笔者关注的重点.那么，在数学教学中，如何逐步培养学生提出问题的能力呢？结合自身的教学实践与反思，我们认为，在数学课堂中培养学生提出问题的能力，需要让学生经历从敢于提出问题、能够提出好问题到乐于提出真问题的过程，即谱好“敢问曲”“善问曲”和“乐问曲”三部曲.

一、谱好“敢问曲”：从“定式”到“变式”，让学生敢于提出问题

（一）以教学模式之“变”提升学生提问信心

为了引导学生敢于提出问题，教师除了依靠传统数学教学惯用的“教师出题、学生解题”模式，更需要营造一种“让学生发现和提出问题”的民主氛围，引导学生具有数学问题意识.一方面，教师要给予学生充分提问的机会，提问的机会不限于课堂上，也不限于教材中，鼓励学生随时随地提出各种各样的问题;另一方面，教师应该关照每一个学生，尽量给予学生公平的提问机会，尤其要鼓励在课堂上相对“沉默”的学生提出问题，关注生生对话、生师对话，并且要保证这种对话的民主性与平等性.即教师应帮助学生克服教学活动中的困难恐惧或害羞心理，为学生提供轻松提问的机会与环境，鼓励学生提问，并及时给予鼓励和认可.即使学生提出的问题很简单甚至是并不合理，也不应嘲笑或批评学生，而应该耐心地引导，带领他们继续思考，逐步形成更有逻辑、更有信心的提问.

【案例1】

沪教版《数学》九年级第一学期《相似三角形的性质④》教学中，笔者设计了如下例题变式.

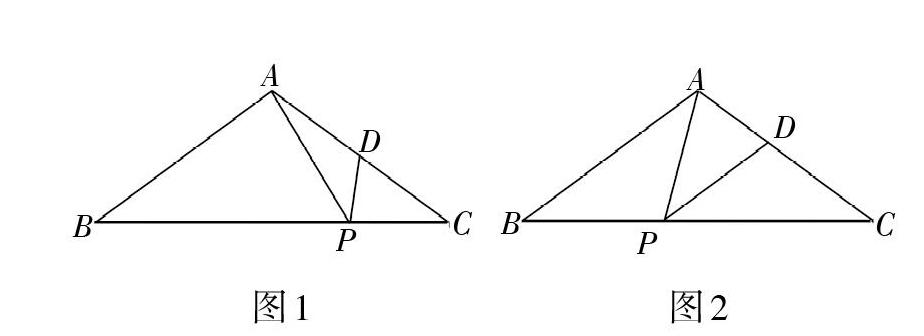
题目    如图1-1（图略），在△ABC中，AB = AC = 10，BC = 16，点 P、D 分别在边BC、AC 上，BP = 12，∠APD = ∠B，求 CD的长.

变式1：如图1，在△ABC中，AB = AC = 10，BC=16，点P、D分别在边BC、AC 上，∠APD = ∠B，如果BP = 2CD，求CD的长.

变式2：如图2，在△ABC中，AB=AC= 10，BC=16，点P、D分别在边BC、AC上，∠APD = ∠B，如果PD[?]AB，求CD的长.

变式3：如图1，在△ABC中，AB = AC = 10，BC = 16，点 P、D 分别在边BC、AC 上，∠APD = ∠B，__________，求CD的长.（请在横线上填写一个条件编制一道题目，并解答）

在例题教学中，引导学生关注相似三角形的基本图形，“变式1、2”将例题条件“BP=12”换为“BP=2CD”或“PD[?]AB”，学生体会到能确定BP即可求得CD.通过这个条件变式能发现“知道BP的长或者与BP有关的数量关系，也是可以求得CD的长”.通过“例题”与“变式1、2”的层层铺垫，为学生搭建了脚手架，学生的思维接近最近发展区，为“变式3”提供思考的路径与方式，学生就可以自己提出问题，并且检验所提问题的正确性，发展数学高阶思维.学生提出“如果PD⊥BC”“如果PD⊥AC”等线段的位置关系，甚至有学生提出“如果△APD是直角三角形”“如果△APD是等腰三角形”的问题，后面这两个问题解决需要分类讨论，所以学生的批判性思维、创新性思维得以激发.

（二）以教学情境设计之“变”激发学生提问动机

学生的自我意识和内在动机是提高学习效果的最佳支持，所以激发兴趣并充分调动学生的主动性是激发学生自己思考和提问的动机之一.利用学习资源创设问题情境是激发学生学习和探索兴趣的有效途径，要引导学生敢于提出问题，应从着眼于问题本身的设计转变为能够引导学生“发现和提出问题”的情境设计，为学生的数学学习埋下“发现和提出问题”的“种子”.

在数学课堂活动中，教师可以引导学生从教材插图、日常生活、俗语、数学实验现象以及自己的体验中提出问题.具体来说，首先，教师要根据学生的最近发展区，为学生提供“跳一跳”能够到的学习目标，恰当的目标指引会激发学生在合适水平上的学习动机;其次，教师要为学生设置便于认知冲突产生的情境，只有当学生内部认知产生冲突，感到疑惑不解的时候，他们积极主动发问的热情才会被点燃;最后，教师应该在课堂教学中重视评价，针对不同类型的问题，运用不同的评价手段，对学生提问做出积极与充分的反馈，让学生体验到提出问题、认识问题、解决问题、反思问题这一完整历程.

【案例2】

沪教版《数学》七年级第一学期《中心对称》教学中，笔者设计了如下“两个图形成中心对称的性质”的探究活动.

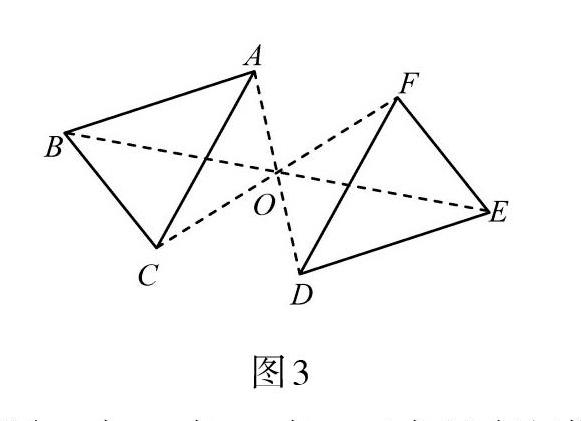
如图3，△ABC与△DEF关于点O成中心对称.

活动：利用几何画板，观察测量数据.

问题1：对应线段、对应角有怎样的数量关系？

问题2：点A、点O、点D三点具有怎样的位置关系？

问题3：线段AO、线段DO具有怎样的数量关系？

问题4：你能说说“问题1”的原因？你还想提出什么问题？

活动中，学生通过几何画板的测量，带着“问题1”到“问题3”，观察测量数据，更好地探究中心对称性质.由于七年级的学生还未进入系统的论证几何学习，仅仅只能感知数据得出结论，因此对于结论的缘由不会特別考虑.通过“问题4”引导学生思考“对应线段、对应角相等”的缘由是“两个图形成中心对称”，即△ABC与△DEF 重合.同时，引导学生对“问题2、3”的结论提出“为什么”的新问题.在这个过程中，教师首先要肯定学生主动思考问题的积极性和敢于提出问题的勇气，通过问题的层层递进，制造质疑辩惑的氛围，让学生学会思考，引导学生提问.每一个提问的学生能感受到教师的信任和尊重，能够促使他们敢于提问，从而增加他们进行探究学习的动力.

总的来说，学生应该置身于学习情境，通过发现问题和提出问题，增强自身对于学习的参与感和获得感，这有利于提升学生主动提问的意愿，激发学生提问的主动性.学生可以通过学习体验成功的乐趣，获得内心的成就感和自我能力的理解.这种成就感强而有效且持久.这也是将激励转换成学习动力的最好方法.在课堂教学过程中，教师必须抓住学生在课堂上的引燃点，给予学生肯定，根据学生的心理特性，用各种各样的方法来回应学生的兴趣和情感等心理需求，从而产生积极提问的内部动机.

二、谱好“善问曲”：从“提出问题”到“提出好问题”，让学生善于提问

培养学生“发现和提出问题”的能力不是一项短期任务，有了发现和提出问题的“种子”，教师便可以通过多元方式搭建脚手架，逐步引导和帮助学生提出有价值、高层次的问题，让“种子”生根发芽.为了使问题明晰、科学，教师可以编纂一些预习提纲，或教给学生一些通用提问的角度和方法，目标指向学生更有效地提出问题.

（一）从概念、公式、定理的理解与辨析中找寻疑点

在学生理解数学概念的含义后，引导学生从以下角度思考问题：这个概念揭示事物的本质是什么？其内涵有什么特点？它的外延是什么？它以什么形式定义？有多少种定义方式？如何比较它们的特点？与其接近的概念是什么？它们在内涵和外延上如何关联？在概念理解时，可能会出现怎样的错误？等等.

在学生知道数学公式的意义后，引导学生从以下角度思考问题：如果一个公式是从现有的数学知识中推导出来的，那么推导该公式的基础是什么？有多少种方法可以得出这个结论？有什么条件限制？这些条件可以增加或减少吗？条件增减后，公式及其适用范围有何变化？该公式的适用范围是什么？如何用它来解决相关的数学问题和实际问题？该公式的形式可以简化吗？它有什么特别之处？你怎么记忆公式？等等.

在学生理解了定理所陈述的事实之后，引导学生从以下角度思考问题：该定理的条件是什么？它有什么作用？可以减少吗？该定理的条件和结论可以互换吗？交换后的命题正确吗？如何用数学语言表达这个命题？在应用定理时，可能会出现什么错误？这些错误通常发生于什么情形下？ 等等.

【案例3】

沪教版《数学》八年级第一学期《函数的概念》教学中，有关“函数概念”的活动设计如下.

活动：观看视频《汽车加油》（在加油站加油的过程中，加油器显示器上的费用数据随着油量的上升而上升）.

问题1：描述汽车加油这一变化过程中有哪些数量？

问题2：哪些量的数值保持不变？哪些量可以取不同的数值？

问题3：有几个变量？变量之间有怎样的联系？

问题4：如果油量设为x升，总价为y元，能用含x的式子表示y吗？

问题5：油量x升可以取任意值吗？为什么？

问题6：你还有什么疑惑？还能提出什么问题？

活动中，学生通过有关实际生活引发的问题，抽象出函数的概念.在解决“问题1”至“问题5”的过程中感受到每个问题就是概念的一个切入点，创设的问题情境引发了学生的深度思考，在逐层递进的问题中，学生抽象出函数概念.当“问题1”至“问题5”解决以后，进入“问题6”，教师询问是否还有其他疑惑可以进行小组讨论的时候，有学生竟然提出“总价y为油量x的函数，那么油量x是否为总价y的函数”，这样引发课堂的又一次讨论，将函数概念的难点“当一个变量取一个确定的值时，另一个变量的值也随之唯一确定”突破.通过教师创设的问题情境以及设计的递进问题，激发学生提问的主动性，通过发现问题和提出问题，增强自身对于学习的参与感和获得感.在教学过程中，教师抓住学生在课堂上的引燃点，给予学生肯定，逐步得出函数的概念，这样的活动设计有助于学生养成良好的思维习惯，勇于怀疑，大胆创新，勇于自我提问.

（二）从问题解决的过程与解题过程的错误中探寻疑窦

数学学习与问题的解决紧密相关.“用新方法来解决老问题，可以推动纯粹数学的发展，当我们对老问题有了更好的理解，自然会提出新问题.”[1]因此，应鼓励和指导学生在问题解决过程中或解决问题后发出疑问：现有的解决方案是什么？问题解决过程中的关键点是什么？考试中常见的错误有哪些？用什么基本知识和公式来解决这个问题？应用程序中有无条件限制？有多少种方法可以解决这个问题？他们的思维有哪些相似点和不同点？在解决问题的过程中容易犯什么错误？哪里容易出错？错误的原因是什么？该问题可以使用相关的知识改编成新的命题吗？等等.以上问题归结起来，就是用“一题多解”“一题多变”和“编拟新题”来激发学生的创造性.

【案例4】

沪教版《数学》八年级第一学期《二次根式及其性质》教学中，有关二次根式性质综合应用，设计问题：已知[5=m]，[50=n]，用含m、n的代数式表示[2.5].

一名学生出示解法1：[2.5=2510=250100=5×5010=mn10];另一名学生展示解法2：[2.5=25×0.1=5×0.1].因为[0.1=110=550=550=mn]，所以[2.5=5×0.1=5mn].当两名学生出示了两种解法后，顿时课堂沸腾了，学生们不能确定哪位同学正确，看似两种解法都正确，那为什么有两种表现形式？

生：到底哪位同学的答案正确？

师：很好的问题，同学们是否可以小组讨论一下？然后展示自己的想法.

在討论中，学生发现这两位同学的答案都是正确的，只不过表现形式不同，进而引发学生提出“为什么会有不同表现形式”的问题，然后教师引导学生进一步探究其原因.不同的解法引发学生的疑问，小组讨论探索，教师适时引导，有助于提高学生思维的敏捷性、批判性和提问能力.在问题解决的过程中，教师故意在课堂教学中留下一些不足或遗漏，以促进学生的学习，提高机敏性并形成对问题的批判性观点，这将有助于学生发现问题和提出问题.

三、谱好“乐问曲”：在与现实世界的链接中体悟提问价值，让学生乐于提问

现实世界是数学教学的真实情境，数学源于生活并为生活服务.现实生活和生产实践包含许多数学运算和數学关系.与现实世界的链接有助于学生提问的“种子”开花结果，教师可依托“书本数学”到“生活数学”或“生活数学”到“书本数学”双向探究的途径，引导学生用数学思维解释和解决生活实际问题、在真实情境中发现和提出数学问题，从中体悟数学与生活、数学与其他学科知识之间的联系.只有学生自己感受到看似抽象的数学与现实世界的相关性、在现实生活中的“有用性”，才能更好地养成用数学思维看待现实世界、解决现实问题的意识和能力，体悟到提问的价值，从外部驱动的提问逐步发展为自己乐于提问，为学生数学问题意识的持续性、提问能力的发展性提供动能，同时，通过与现实世界的链接，不断触及数学学科的本质，学生提出真问题的能力也能够不断提升.

教师应引导学生用数学的眼光观察周围发生的现象，鼓励学生在面对周围的现象时经常问问自己：“这些现象可以和什么数学知识联系在一起？我们如何利用这些知识解释现象或解决问题？”教师通过数学建模，引导学生对客观事物所包含的数学关系提出数学问题.

【案例5】

在沪教版《数学》九年级第一学期《解直角三角形的应用②》教学中，笔者给学生布置如下长作业：“如图4，研究发现，科学使用电脑时，望向荧光屏幕画面的视线角[α]约为20°，而当手指接触键盘时，肘部形成的手肘角[β]约为100°.图5是其侧面简化示意图，其中视线AB水平，且与屏幕BC垂直.”请编制有关科学使用电脑的试题.

学生在课后查找资料后，根据自己对所学知识的理解，对科学使用电脑这些资料进行再加工、再创造后，编拟出新的数学问题.“①若屏幕上下宽BC=20cm，科学使用电脑时，求眼睛与屏幕的最短距离AB的长;②若肩膀到水平地面的距离DG=100cm，上臂DE=30cm，下臂EF水平放置在键盘上，其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°？”

总之，在数学教学中，主动加强对学生提问能力的引导是教师义不容辞的责任.但这是一项困难的任务，因为学生提问并不容易，关键是要依靠教师的指导.因此，在数学教学中，教师应尽量激发学生提问的积极性，营造提问的氛围，创设提问的情境，引导提问的方法，逐步培养学生的提问能力，最终让学生自己有提问的能力.

参考文献：

[1]沈佩群.如何培养学生“提出问题”的能力[J].教学与管理，2002（24）：38-39.