展示性学习视角下数学图形特征的探索

仇小婉 段志贵

【摘   要】展示性学习有助于学生实现自我，与其他学习者共同成长。把展示性学习应用于“三角形三边关系”教学之中，灵活运用“做”“展”“启”“练”“评”等方式方法，引导学生发现图形特征，体会三边关系，能够充分调动学生的学习积极性、主动性和创造性，有效构建师生、生生自由平等交往的生态化课堂环境，培养学生的数学思维，提高学生的数学素养。

【关键词】展示性学习;数学图形特征;三角形三边关系

展示性学习是一种凸显儿童自主学习与合作交流的学习方式，具体地说，它是个人或学习共同体通过向他人展示知识、方法、疑难、困惑等，以实现自我，和其他学习者共同成长的学习方式[1]。下面以苏教版四年级下册《三角形三边关系》一课为例，分析展示性学习方式在数学图形特征探索活动中的具体应用。

一、展示性学习的教学构思

虽然每名学生的成长环境不同、个性不同，表现出的基础特质也不相同，但他们各有各的优势，各有各的不足。诚如美国著名学者、心理学大师唐纳德·克利夫顿所说，“教育的目的就是发现优势并发挥优势”，学校教育就是要唤醒他们，激励他们，让他们保持和发扬优势，修正或弥补不足。本质上，展示性学习就是要让每名学生都有展示的机会，使他们能够充分发挥自己优势并在学习的过程中逐步建立起成长的自信。相比传统的小组合作学习，展示性学习不仅关注小组内知识和方法的交流，还注重小组代表和全班同学的交流学习，学生可以在辨析与交流中丰富学习内容，进行更深度的学习思考。因此，扎根于“唤醒—展示—成长”理念的展示性学习策略在小学数学教学中的运用，具有十分重要的现实意义和实践价值。

三角形的三边关系特征，即任意两边之和大于第三边，是学生在学习三角形定义之后对三角形“边”基本特征的初次研究。教学上采用展示性学习的方式，组织学生开展动手操作——围三角形的探索活动，并让学生先后在小组和全班进行展示交流，再通过教师的有效点拨及有针对性的巩固训练，促进学生更深入地理解三边关系的数学本质。

二、展示性学习的推进过程

展示性学习的实施主要包括合作探究、 展示交流、精讲点拨、有效练习和创新评价等具体策略，常常简称为“做”“展”“启”“练”“评”。这五项策略并非完全割裂，也不固化为固定的时间、统一的模式，而是可以根据实际需要灵活推进，优化组织。一般情況下，“做”在展示之前完成，“展”“启”“练”“评”交互进行。在小学数学图形特征的展示性教学中，教师着重组织以下三个环节的教学。

（一）小组合作，展示前“做”中学习

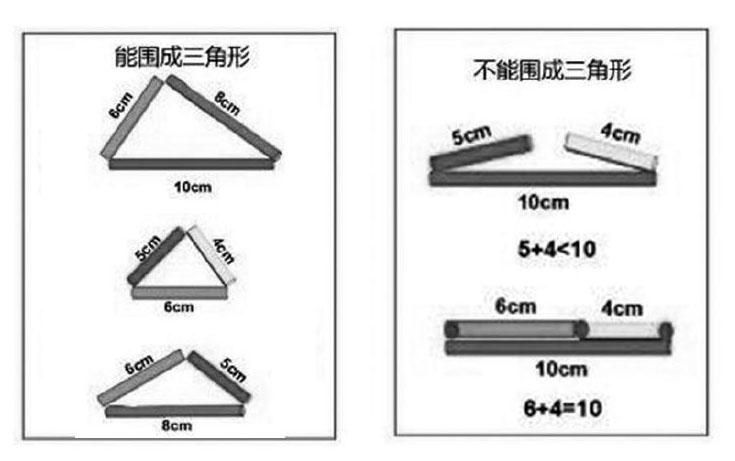
上课初始，教师首先让学生任意选取小棒围三角形，发现有能围成三角形和不能围成三角形两种情况，在此基础上顺势而教，引导学生研究三角形三边长度关系。

小组合作1：从学具内任意选择3根颜色不同的小棒，围一围，并记录在学习单上。

[第一条边 第二条边 第三条边 是否能围成三角形（打√或×） ]

学生选择颜色不同的3根小棒独立围三角形，小棒颜色不同即长度不同，同时请小组记录员将每人围的情况一一记录下来，教师在组内巡视指导。

小组合作2：从围成三角形的小棒中任选2根，和第3根比一比，你发现了什么？

学生观察比较围好的三角形，思考三角形中任意2根小棒与第3根的关系。

小组合作3：刚刚我们只是从3个三角形中发现任意两边之和大于第三边，能说明所有三角形都这样吗？（不能）这只是我们的猜想，还需要通过更多的例子来加以验证。怎么验证呢？小组讨论交流。

小组的有效交流应基于对所有学生动手操作结果的展示与思考。只有每名学生都有机会动手操作，课堂展示才会呈现出真实性和多样性。如果仅靠一两个小组与教师的互动交流完成学习，那么课堂呈现出的是虚假的热闹，不利于全体学生发展。因此，在展示前小组内应先进行分工，组内成员一起动手操作围三角形，获得体验，并初步形成猜想，为真实有效的课堂展示打下基础。

（二）激发思考，在“展”“启”中提升思维

汇报展示1：小组合作完成第一个任务后，请各小组汇报展示围三角形的情况。

第一小组：我们小组用10厘米、6厘米和8厘米这三根小棒围成了1个三角形，用4厘米、5厘米和6厘米这三根小棒围成了1个三角形，还用5厘米、6厘米和8厘米小棒围成了三角形。

师：那有没有小组没能围成三角形的？

第四小组：我们小组用4厘米、6厘米和10厘米这三根小棒没围成三角形。

师（点头）：嗯，怎么会出现这种情况呢？其他小组呢？

第五小组：我们小组用10厘米、4厘米和5厘米也没能围成三角形。

师：我们来看一下，为什么这两种情况不能围成三角形？

学生展示围三角形的各种情况后，教师引导学生先研究三根小棒不能围成三角形的情况，发现用数学算式表示这两种情况中三根小棒长度关系，分别是4+5<10和6+4=10，进而猜想能围成三角形的三根小棒的关系：两根小棒的长度加起来大于第三根小棒的长度。

汇报展示2：比较三角形中任意两根小棒与第三根的关系。

小组汇报：我们小组先研究第1个三角形，6+8>10，6+10>8，8+10>6。然后研究第2个三角形，4+5>6，6+4>5，6+5>4。最后研究第3个三角形，5+6>8，5+8>6，8+6>5。我们小组发现：三角形中任意两根小棒长度之和大于第三根小棒的长度。

师：在三角形中，小棒其实相当于三角形的边，我们还可以换一种说法：三角形中任意两边之和大于第三边。这句话中“任意”是什么意思？

这里教师的追问即为“启”。“启”很重要，是提升学生思维层次的关键环节，不能错过。

师：刚刚在比较时我们有没有体现出“任意”？

学生思考片刻，逐渐理解：在比较三角形两边之和与第三边关系时，对应写出三道算式，将三种情况都进行比较，这就是“任意”的体现。

师：可是每次比较时都写这么多算式很麻煩，有没有简单点的方法？

生：其实只要写出一道就可以了，第1个三角形中只要写出6+8>10，第2个三角形只要写4+5>6。

师：为什么？

生：这是比较了较短的两边之和与第三边的长度。较短两边之和都大于第三边了，三角形中其他任意两边之和肯定大于第三边。

教师随即点拨：既然有较短边，相应的就有最长边。我们在比较时不需要把所有情况都写出来，只要比较短两边之和与最长边之间的关系就可以了。

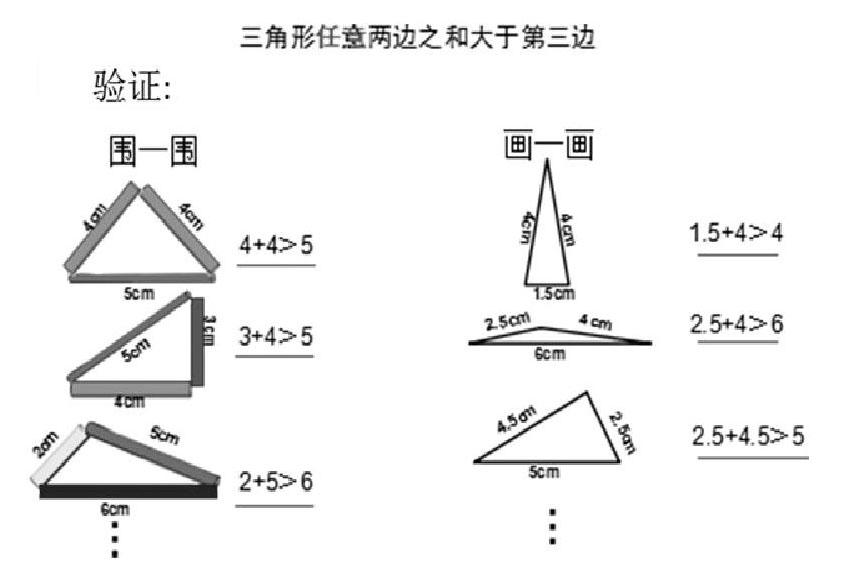
汇报展示3：由3个三角形的三边关系初步提出猜想后，在组内验证其他三角形是否也满足这一猜想，并介绍交流验证的过程和结果。

以上教学过程，教师引导学生通过动手操作和不完全归纳，在众多实例中发现其他三角形同样满足这一猜想，并且没有出现反例，大家形成共识：三角形任意两边之和大于第三边。其中，在验证猜想时，学生通过自己画三角形发现：三角形三边的长度不仅可以是整数，小数也同样适用，扩大了三角形三边的取值域。

（三）巩固训练，在“练”“评”中深化认知

练习1：从学校到少年宫有几条路线可以走？走哪一条路最近？

练习1的解决并不困难，重在通过问题解决发展学生的推理能力。学生提出猜想，并通过举例验证获得结论的方法是一种合情推理。在小学教学中很多地方会用到合情推理，但合情推理的结果本身不够严谨，所以教师在进一步的讨论中隐去“学校—邮局—少年宫”的路线，引导学生观察上面的三角形，感受从“两点之间线段最短”得出“三角形任意两边之和大于第三边”的演绎推理思想。这样合情推理与演绎推理相辅相成，凸显思维的创新与跃进，符合学生的思维特点，帮助学生从另一个角度再次探索知识，感受数学的趣味性，增强思维的灵活性。

练习2：（1）李叔叔打算从8厘米、5厘米、4厘米和3厘米长的小棒中，选择3根小棒钉成1个三角架，可以选择哪3根？

学生选择3根小棒，并自觉用算式验证是否能围成三角形。

（2）李叔叔最后选择了8厘米、5厘米和4厘米的小棒，如果把其中的4厘米小棒换掉，可以换多长的？

教师结合视频，帮助学生理解在比较三角形任意两边和与第三边时，最长边不一定是固定的，而是可以变换的。将8厘米看作最长边，第三边要大于3厘米却不超过8厘米;也可以将第三边看作最长边，这时第三边大于等于8厘米，却要小于13厘米。由此得到第三边的取值范围：小于已知两边之和，大于已知两边之差。

以上练习能帮助学生在思考中提升对知识的理解，深入理解三角形三边关系，自觉检验三角形第三边的范围，感受解决问题过程中数学思维的层次性和操作方法的灵活多样性。

三、展示性学习的教学反思

（一）尊重学生主体地位是展示性学习的前提

本节课基于学生是学习的主体，教师是学生学习的组织者、引导者、促进者的基本理念，放手让学生自主探索、汇报展示和交流。通过独立围三角形、小组展示、提出猜想、举例验证并获得结论这一过程，学生得以充分展示自主学习的成果。自由发言、动手操作等活动贯穿始终，激发了学生学习的内驱力。正因为有对学生主体地位的尊重，才有后面课堂中展示汇报的精彩。课堂上每个人都积极参与，认真思考，群策群力，课堂氛围活泼真实，有效地提高了学习效率，增强了学习效果。

（二）实现全体学生共同发展是展示性学习的目标

本节课学生先独立围三角形，然后以小组展示汇报为平台，通过展示，调整完善自己的认知;通过倾听同伴的补充发言，形成新的信息。“任意”是数学推理中重要的词语之一，多数学生头脑中原本的“任意”指随意、随便的意思，他们并没有深入理解本质。小组讨论并阐释对“任意”的理解，从语言、算式等不同方面相互交流，学生在吸收集体智慧的过程中，又反过来促进集体的发展，进入新一轮的学习，在这种生生对话、师生对话中实现对“任意”的深入理解。这种学习展示体现了生命的两种本性：作为个体的自我需要成长、发展，作为群体中另一个自我需要交流、欣赏或被欣赏、评价或被评价。如此，每个人在数学上都获得不同的发展，整个学习共同体在课堂教学中焕发了生命的自然活力。

（三）开展行之有效的探究活动是展示性学习的载体

本节课的教学目标之一是引导学生理解和掌握三角形的三边关系特征，即任意两边之和大于第三边。教学上采用小组合作的形式，沿着猜想—验证—结论—应用这一线索组织学生通过组内和组际间的互动与展示，开展动手围三角形的探索活动，在活动中教师辅以示范与启发，引导学生发现图形特征，体验三角形任意两边之和大于第三边。如果不安排围三角形的活动，也不汇报展示围的情况并比较三角形的三边关系，而是直接告诉学生结论，尽管也能完成教学，但学生的体验和理解不会如此深刻，综合能力得不到明显提高，学习效果也不会像现在这样显著。开展行之有效的探究活动，可以促进展示性学习，充分调动学生主动性和创造性，构建师生、生生自由平等交往的生态化课堂环境。

综上，在展示性学习视角下开展图形特征的探索，促使学生不仅可以从被动地“听”转向主动地“做”，拥有更多自由表达、与他人交流的机会，获得对数学知识的深度理解，还可以通过小组共同合作和展示，对自己所在小组产生归属感，改变全班学习氛围，让知识、能力和情感自然发展，互相促进。

参考文献：

[1]汪小珍.展示性学习：自主学习的一种样态[J].教育研究与评论，2020（2）：23-24.

[2]韩立福.展示对话学习   焕发生命活力[N].中国教育报，2012-08-09.

（江苏省南京市将军山小学   210012

盐城师范学院数学与统计学院   224002）