特定树和单圈图下的增强型萨格勒布指数

甘 露，杜 颖，曹晓丽

（湖北师范大学数学与统计学院，湖北 黄石 435002）

0 引 言

拓扑指数是分子结构的数学描述符，实现分子结构的数值化，反映分子的拓扑性质.近年来，研究图，尤其是分子图的拓扑指数的性质及应用，受到一些数学化学工作者的关注.1998年，Estrada等［1］提出了原子键连通性指数（atom-bond connectivity index，ABC指数）.该指数的定义为

其中E(G)是边的集合，du和dv分别是点u和点v的度.在 2010年，Furtula等［4］提出了图的增强型萨格勒布指数（augmented Zagreb index，AZI），该指数的定义为

该指数的预测能力已被证实在研究烷烃的热形成中，比ABC指数的预测能力更强，由于AZI提出时间不长，目前的研究成果不多，其部分数学性质在文献［2-7］中已被研究.本文将计算一些特定树和单圈图的AZI.

本文通过给出某些特殊树的AZI，计算某些特殊单圈图的AZI均为连通图，所有点的度不超过4的连通图称为化学图，其分子结构图可能类似于某些图，这是化学中应用图论的一个主要原因.

1 特殊树及烷烃的AZI

分支Bi是使i条长度为2的悬挂路与P2的一个端点v相邻形成的树，显然顶点v在分支Bi中的度为i+1（见图 1）.

图1 分支Bi

图2 树

定理1.1设n和k是正整数（且n≥1，k≥2），树的AZI为

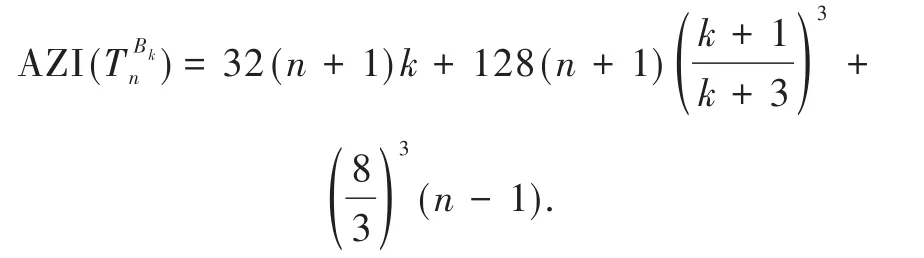
证明在树中，显然有2n+2个Bk分支.在每一个Bk中包含3类边.类型1:该边有2个端点，一端度为1，一端度为2，共有k条此边；类型2:该边有2个端点，一端度为2，一端度为k+1，共有k条此边；类型3:该边的2个端点，一端度为k+1，一端度为4，共有1条此边.路径Pn中有n-1条边且每条边的端点的度都为4.

由图的AZI的定义，得到

烷烃是碳氢化合物，分子中的碳原子都以单键相连，其余价键都与氢结合而成，其化学式为G=CnH2n+2，其骨架结构如图3所示.

图3 CnH2n+2骨架结构

定理1.2设n≥1且n∈N+，则图G=CnH2n+2（烷烃）的AZI指数为

证明用数学归纳法证明，当n=1时，G=C1H4，骨架结构如图4所示.

图4 C1H4骨架结构

当n=k+1时，其图为G′，骨架结构如图6所示.

可知，图6在图5的基础上增加了3条边，则图6的AZI为

图5 CkH2k+2骨架结构

图6 G′骨架结构

综上，当n≥1时，图G=CnH2n+2（烷烃）的AZI为

2 特殊的单圈图及环烷烃的AZI

图7 单圈

定理 2.1设n≥ 3，p≥ 1且n，p∈N+，则单圈图的AZI是

证明用数学归纳法证明，当n=3时，则图，于是有

从而当n=3时公式是成立的.假设当n=k(k≥4)时，的 AZI满足公式，现证n=k+1时，的AZI满足公式.单圈图如图8所示，令e表示连接点v1和点vk的边.

图8 单圈

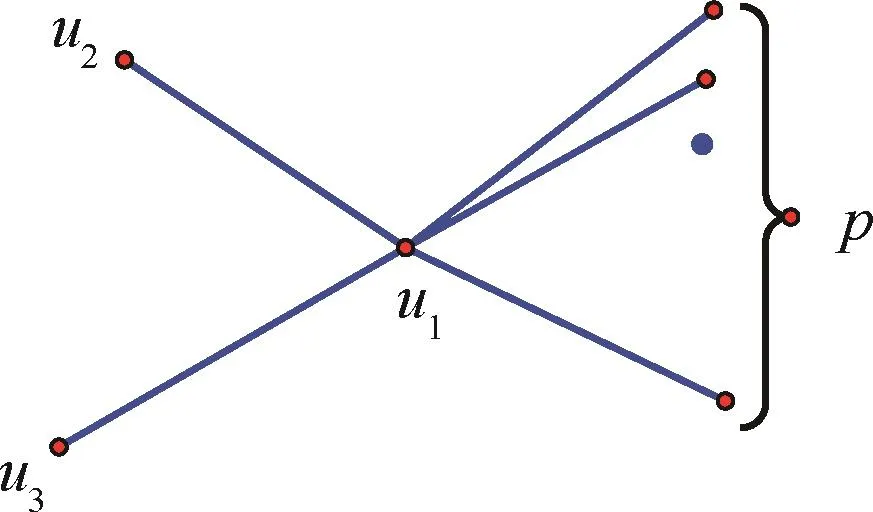
图9 H单圈

令图9中的顶点u1分别与u2、u3和p个悬挂点相连.将H连接到图8上，使u2与v1重合，u3与vk重合，记u1=vk+1，得单圈图（见图 10）.

图10 单圈

可知，图10是在图8的基础上增加了p个悬挂点和一条边，则图10的AZI为

定理2.1中，如果p=2，则可得到化学中环烷烃(CnH2n)的AZI，其骨架结构如图11所示.

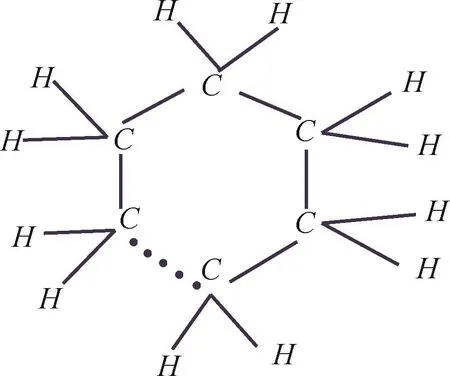
图11 CnH2n骨架结构

推论2.1环烷烃CnH2n的AZI为

证明定理2.1中令p=2可得.