结合加权KNN和自适应牛顿法的稳健Boosting方法

罗森林， 赵惟肖， 潘丽敏

(北京理工大学 信息与电子学院，北京 100081)

Boosting是模式识别和机器学习领域中一类重要的集成学习算法，它可以将分类准确率仅比随机猜测略好的弱学习器增强为分类准确率高的强学习器[1-2]. 在各种Boosting算法中，AdaBoost[3]是第一个成功将其思想应用在实践中的算法，并在代价敏感分类[4]、邮件过滤[5]、人脸识别、视频跟踪[6]等诸多问题上表现出优异的性能，在学术界和工业界被广泛使用.

AdaBoost算法的思想是，在每一轮迭代中，不断加大错误分类样本的权重，降低正确分类样本的权重，使分类器聚焦于被错分类的样本. AdaBoost通常有着很好的泛化能力，不易过拟合[3]. 然而，当训练数据含有较多标签噪声时，被错分类的样本往往是噪声样本，AdaBoost的指数损失函数使得错分类的噪声样本的权重以指数速率增加，迫使子分类器过度关注噪声样本，导致学习效果的急剧下降[7]. 在复杂的真实数据中，常常包含不可忽略的噪声，例如，在生物医学数据中，很难得到不含任何噪声的样本标签. 因此，使AdaBoost算法克服噪声敏感性并在噪声环境中表现地更加稳健，是其理论和应用研究的重要方向[8].

现有AdaBoost抗噪算法的研究主要包括控制样本权重的调整、删除可疑样本和优化损失函数3种改进方向. 其中，先删除可疑样本再进行训练的方式能够简单有效地排除部分噪声样本的干扰，但这种硬性的处理会造成少数正常样本的丢失，同时无法排除训练集中其他未被明确识别的噪声样本；通过选用比AdaBoost的指数损失更平滑的损失函数，可以使得错分类样本的权重以低于指数速率增长，从而减弱对错分类样本的关注，减少噪声带来的损害. 但现有大多数方法的损失函数都是固定的，无法对错分类的正常样本和噪声进行有效区分.

随着AdaBoost算法在1996年的提出，针对其噪声敏感性问题的改进算法不断涌现. 现有的AdaBoost抗噪算法的研究主要包括控制样本权重的调整、删除可疑样本和优化损失函数3种改进方向.

① 控制算法迭代中的权重调整方向，从而减少训练集中噪声样本或异常值的影响. MadaBoost[9]算法记录训练集各样本的初始权重，在迭代中进行权重有界化处理，防止出现权重任意扩增的情形. RADA[10]算法在迭代过程中引入记忆因子，记录样本权重的增减过程，从而更好地调整那些反复错分样本的权重更新方向.

② 关注错分类的噪声样本本身，先删除可疑样本再进行训练. Vezhnevets[11]直接对可疑样本进行删除. EdaBoost[12]算法使用加权KNN识别可疑样本，并对这些样本的权重赋予0值. Angelova[13]通过在原始训练集上采样，训练多个分类器对样本进行判定，若不同分类器判定结果差异性较大，则视为噪声并删除，从而避免可疑样本的干扰.

③ 选用比AdaBoost的指数损失更平滑的损失函数，使错分类样本的权重不再以指数速率增长. LogitBoost选择Logit函数代替AdaBoost中的指数函数，使错分类的噪声样本的权重以对数速率扩增，扩增速度较指数损失更缓慢. SavageBoost[14]算法优化的Savage损失函数不会无限制地增大对错分类样本的惩罚，因此降低了算法对噪声数据的敏感性. RBoost[15]算法在Savage函数的基础上改进得到了更平滑的Savage2损失函数. SPBL[16]算法将自步学习的思想运用在AdaBoost上. CBAdaBoost[17]算法采用了3种置信度准则进行样本嫌疑大小的估计. 部分研究直接优化0-1损失，这是一个NP难问题，只能做近似处理[18].

针对现有删除可疑样本和优化损失函数改进方法中存在的问题，本文提出一种结合加权KNN和自适应牛顿法的稳健Boosting方法RLBoost(revised-logit-loss boosting method). 首先，对可疑样本不进行硬性的删除，而是采用加权KNN进行预处理，得到所有样本的噪声先验概率，对样本的噪声可能性进行评判. 其次，通过将噪声概率参数引入Logit损失，构建能根据噪声概率提供不同权重扩增策略的损失函数，使噪声概率低的样本的权重仍能以较快速度增长，以便分类器更好地学习这些难以正确分类的样本，同时给予噪声概率高的样本较大的惩罚，迫使分类器尽可能少地关注噪声样本，从而实现对错分类的正常样本和噪声的有效区分. 最后，采用自适应牛顿法进行损失函数的优化求解，自适应牛顿法[9]是Boosting常用的损失函数求解方法，和AdaBoost的前向分步可加模型相比，能够利用二阶导数信息，求得损失函数条件期望的更准确下降方向. 实验结果表明，和其他Boosting稳健算法相比，提出方法在不同噪声水平下均表现出较高的稳健性，在真实医疗数据集上的不同评价指标结果均有一定提升.

1 改进算法理论基础

1.1 Logit损失分析

LogitBoost使用比AdaBoost的指数损失更平滑的Logit损失函数. 图1为指数损失函数和Logit损失函数的示意图，其中横轴为分类间隔yf(x)，纵轴为损失函数. 若某样本x的分类间隔为负值，说明该样本被错分类，负数的绝对值越大，说明该样本被错分类的结果越可信. 如图 1所示，指数损失函数随分类间隔的增加呈φE=e-yf(x)的指数型增长，意味着在每次迭代中，错分类样本的权重会以指数速率增加. Logit损失函数随分类间隔增加呈φL=ln(1+e-2yf(x))的对数型增长，在含有较多标签噪声时，错分类的噪声样本的权重以对数速率扩增，扩增速度较指数损失更缓慢. 但Logit损失函数同样会出现随分类间隔增加，损失无限增长的情况，造成噪声样本权重在每轮迭代中持续累加，子分类器聚焦于不应过多关注的噪声样本，最终将分类器引导向错误的学习方向.

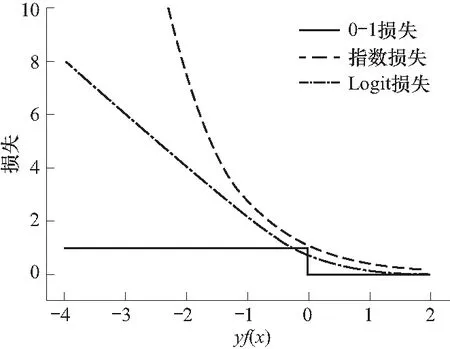
图1 指数损失函数和Logit损失函数Fig.1 Exponential loss function and Logit loss function

1.2 Logit损失的自适应牛顿法求解

LogitBoost算法使用自适应牛顿法进行损失函数的求解，与AdaBoost算法使用的前向分步可加模型相比，自适应牛顿法具有更稳健的学习效果，可以求解每一轮迭代的理论最优子分类器[19]. Boosting以线性可加方式优化损失函数的期望，每一轮迭代在现有分类器F(x)的基础上，加入新的子分类器f(x)，使损失函数的期望尽可能多地减少[20]. 利用泰勒公式将损失函数L(F(x)+f(x))在现有分类模型F(x)处展开到二次为

(1)

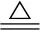
F(x)←F(x)-s(x)/H(x)

(2)

在每一步迭代中需要计算∂L/∂F|f(x)=0和∂2L/∂F2|f(x)=0，当损失函数为φL=ln(1+e2yf(x))时，可得到LogitBoost每一轮迭代的最优子分类器为

(3)

(4)

若样本的概率估计p(y=1|x)和p(y=-1|x)接近0.5，说明该样本在决策边界的附近，错分概率高. 反之，当两者的值越接近0或1时，说明该样本错分概率越小，结果可信度越高. 据此对样本权重w进行更新

w←p(x)(1-p(x)).

(5)

LogitBoost[19]算法实现的伪代码如下，具体实现步骤如下.

Algorithm：LogitBoost

Input：训练样本集S{(x1,y1),…,(xN,yN)}，

fort=1,2,…,Tdo

2 更新权重wi=p(xi)(1-p(xi))

3 以权重wi计算xi到zi的加权最小二乘回归，得到子分类器ft(x)

end for

输入二分类训练样本集，初始化时对所有训练样本的权重做归一化处理，设定样本的概率估计p(x)为1/2，设置算法迭代次数为T.

在算法迭代过程中，根据式(3)计算响应(步骤1)，根据式(5)更新样本权重(步骤2). 通过拟合加权样本到响应的最小二乘回归，求解子分类器ft(x)(步骤3). 集成子分类器得到迭代过程中的分类模型F(x)，由式(4)计算样本的概率估计p(x)(步骤4).

输出为迭代训练得到的各子分类器集成的强分类器.

2 RLBoost算法

2.1 原理框架

结合加权KNN和自适应牛顿法的稳健Boosting方法原理框架如图 2所示，方法通过基于加权KNN的噪声预判断，得到所有样本的噪声先验概率. 将概率参数与Logit损失函数融合，构建能根据噪声概率提供不同权重扩增策略的损失函数，并使用自适应牛顿法进行损失函数的优化求解. 在每次迭代中，综合考虑分类结果和噪声概率作为指导下次迭代中子分类器构建的依据.

图2 结合加权KNN和自适应牛顿法的稳健Boosting方法原理图Fig.2 Principle diagram of the robust Boosting method combining weighted KNN and adaptive newton method

2.2 加权KNN的噪声先验估计

KNN是一种用于分类及回归的非参数统计方法，同时也是最简单的机器学习算法之一. 在进行待分类样本的分类决策时，KNN算法只依据与待分类样本最邻近的K个样本点的类别来决定其所属类别. 加权KNN在KNN的基础上进行了一定改进，给予距离待分类样本更近的样本点更大的权重[21]. 当K值较大时，加权KNN算法中对样本分类起确定性作用的仍是较近的样本点，对K值的选取表现出较高的稳健性.

KNN类算法的核心思想是，特征空间中邻近的样本点大多属于同一类别. 在二分类问题中，若一个正类样本最邻近的K个样本大多为负类，那么这个正类样本有很大可能是噪声. 更进一步地，对于任意样本，若K个近邻中与其有不同标签的近邻个数越多，则可认为该样本是噪声样本的概率越大. 提出算法采用加权KNN计算噪声先验概率，对每一个样本进行数据集的扫描，为其找到K个特征空间中相似度最高的近邻点，再以K个近邻标签的加权投票结果求解噪声概率w

(6)

式中，w的取值范围为[0,1]，w值越大，表明加权KNN方法判断该样本为噪声的概率越大. K表示样本(x,y)在数据集中相似度最高的K个近邻的集合，Dj为第j个近邻的权重，I(yj=-y)在满足第j个近邻的标签和样本标签不同时取值为1，否则取值为0.

2.3 RL损失函数

结合基于加权KNN得到的噪声先验概率，构建RL损失函数(revised logit loss function)，可解决1.2中随分类间隔增加，指数损失和Logit损失无限增长的问题. 新损失函数建立在Logit损失的基础上，此时分类器对训练样本x的预测损失取Logit损失φL=ln(1+e-2yf(x)). 在含样本噪声的问题中，已知y为训练样本包含噪声时的标签，但实际上想要作为标签使用的是样本未包含噪声的真实标签. 设真实标签为z，z是不可观测的，可得到在二分类问题下对应Logit损失φL的期望值

Ez|x[log(1+e-2yf(x))]=P(z=y|x)×

ln(1+e-2yf(x))+P(z=-y|x)ln(1+e2yf(x))

(7)

建立的改进后Logit损失函数φRL为

φRL=w1ln(1+e-2yf(x))+w2ln(1+e2yf(x))

(8)

式中，w1=P(z=y|x)=1-w，w2=P(z=-y|x)=w，w取值由式(6)得到，w2越大，则该样本为噪声的概率越大. 不同w2取值时RL损失函数取值和分类间隔yf(x)的对应关系如图 3所示. 当w2取值为0时，损失函数为Logit损失. 随着w2逐渐增加，样本为噪声的嫌疑加大，RL损失随分类间隔的增加呈现出的增长趋势逐渐放缓. 当w2取值增加到1时，即当判断样本为噪声的概率很大时，随分类间隔的增加，RL损失始终趋近于0. 意味着对于噪声概率高的样本，构建的新损失函数可以解决随分类间隔增加，指数损失和Logit损失无限增长的问题，从而避免噪声样本权重在每轮迭代中持续累加，子分类器聚焦于噪声样本的情况. 而对于噪声概率低的样本，随分类间隔增加，损失仍能以较快速率增长，保证了算法的有效性.

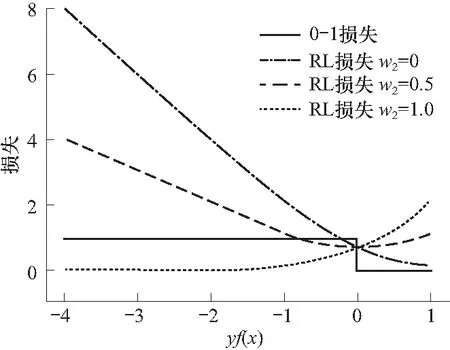
图3 RL损失函数Fig.3 The RL loss function

为严格遵循Boosting理论框架设计噪声稳健Boosting算法，需要证明构建的RL损失函数具有Fisher一致性. Fisher一致性原则要求损失函数L(x,y,f(x))的总体最小化能够收敛到贝叶斯决策. 可以证明AdaBoost使用的指数损失函数以及LogitBoost使用的Logit损失函数都具有Fisher一致性[22].

命题：RL损失函数具有Fisher一致性，即在极限情况下可收敛到贝叶斯决策.

证明：对于优化问题

f*(x)=argminEy|x[φRL(yf(x))|x]

(9)

式中，f*(x)是使公式(8)具有最小期望风险的决策，记η1(x)=P(y=1|x)，η2(x)=P(y=-1|x),代表含噪声后标签为1和-1的概率. 将式(9)展开为

f*(x)=argminLRL=

argmin[η1(x)(w1ln(1+e-2f(x))+

w2ln(1+e2f(x)))+η2(x)w1ln(1+e2f(x))+

w2ln(1+e-2f(x)))]

(10)

期望风险LRL对f(x)求导并令导数为0，求解过程及求得的最优f*(x)为

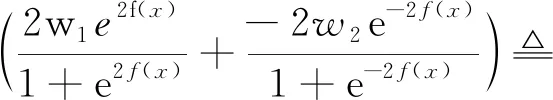
(11)

(12)

式中:η1(x)和η2(x)分别为含噪声时标签为1和-1的情况;w1和w2为判断为正常样本和噪声的概率. 容易得到，η1(x)w1+η2(x)w2是判断真实情况后的P(z=1|x)，同理，η1(x)w1+η2(x)w2是判断后的P(z=1|x)，得到f*(x)为

(13)

2.4 RL损失的自适应牛顿法求解

(14)

(15)

y∈{-1,1}

(16)

由式(13)可求得

(17)

令p(x)=P(z=1|x)，当w1值越大，相应w2值越小时，说明该样本为正常样本的概率越大，可以给予越高权重. 在回归拟合时，选择以w1p(x)(1-p(x))作为样本的权重，进行加权回归，使子分类器更加关注在决策边界附近且噪声概率较小的错分样本. 在RLBoost算法迭代过程中对w1和w2进行更新

w1←w1p(x)(1-p(x)),w2←w2p(x)(1-p(x))

(18)

总结以上过程，可得结合加权KNN和自适应牛顿法的噪声稳健算法RLBoost，算法实现的伪代码如下.

Algorithm：RLBoost

Input：训练样本集S{(x1,y1)}),…,(xN,yN)}，其中y∈{-1,+1}

InitializeF(x)=0，p(x)=1/2,w1i=1-wi,w2i=wi,i=1,2,…,N

fort=1,2…,Tdo

2 更新权重w1i←w1ip(xi)(1-p(xi))，w2i←w2ip(xi)(1-p(xi))

3 以权重w1i计算xi到zi的加权最小二乘回归，得到子分类器ft(x)

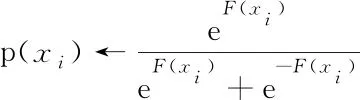
end for

具体实现步骤如下：

输入二分类训练样本集，初始化时对所有训练样本的权重做归一化处理，设定样本的概率估计p(x)为1/2，由式(6)得到每个样本的噪声先验概率w，设置算法迭代次数为T.

在算法迭代过程中，根据式(16)计算响应(步骤1)，根据式(18)更新样本权重(步骤2). 通过拟合加权样本到响应的最小二乘回归，求解子分类器ft(x)(步骤3). 集成子分类器得到迭代过程中的分类模型F(x)，由式(17)计算样本的概率估计p(x)(步骤4).

输出为迭代训练得到的各子分类器集成的强分类器.

3 实验分析

3.1 不同噪声水平下的稳健性验证实验

3.1.1实验数据

实验数据选用来源于UCI的7个二分类数据集，具体见表1. 数据集涵盖心脏病筛查、乳腺X光检查、信用卡申请、政治投票和蘑菇毒性检测等应用场景，包含小样本数据集(270条)和较大样本数据集(8 124条).

表1 实验数据集

3.1.2评价方法

为验证改进Boosting方法在训练集含有不同水平标签噪声时的稳健性，对7个数据集的训练集进行10%、20%和30%比例的标签翻转，引入相应10%、20%和30%水平的标签噪声. 实验选用误差率作为评价指标，误差率越小，则算法在含噪环境中对噪声的敏感性越低，表现越稳健，其中误差率为

(19)

式中，TP、TN、EP和FN分别为将正类预测为正类、负类预测为负类、负类预测为正类和正类预测为负类的样本个数.

3.1.3实验结果和分析

实验在10%、20%和30%噪声水平下，对提出方法和AdaBoost[3]、GentleBoost[19]、LogitBoost[19]、RBoost 4种对比算法的误差率进行比较. AdaBoost的子分类器选用CART分类树，树深度为2，迭代次数为50次. 对于其他所有方法，子分类器算法要求从回归方法中选择，选用CART回归树，树深度为2，迭代次数为50次. 所有算法均以10次10折交叉验证取平均值的方式计算评价指标结果. RLBoost算法选用加权KNN对单个样本为正常样本或噪声进行初步判断，最近邻个数k和权重衰减系数D的可选范围较广，在实验中设定k为5，D为近邻样本与待分类样本间距离的倒数.

各Boosting算法在10%、20%和30%噪声水平下的误差率结果如表2所示，在7个数据集的不同噪声水平下，RLBoost算法的误差率相比其他4种算法均有一定程度的降低.

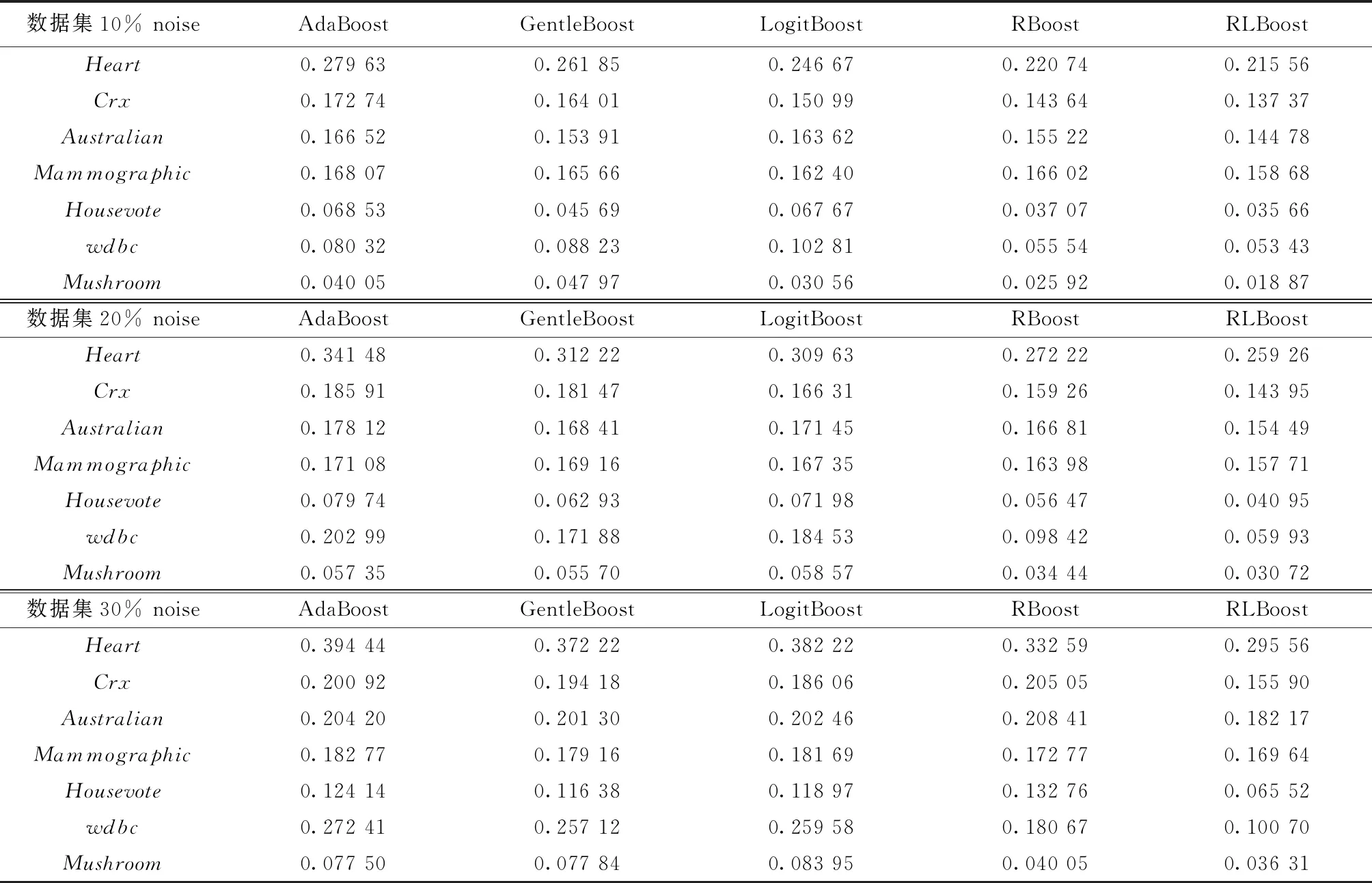
表2 不同噪声水平下的各Boosting算法误差率结果

表2的误差率结果统计排名如图 4所示，在上述的5种Boosting算法的各21组实验中， RLBoost的实验结果表现最优，在21组实验中皆排名第一. 此外，RBoost、GentleBoost、LogitBoost和AdaBoost算法实验结果统计排名前3的实验个数分别为17、13、10和2，RBoost在4种对比实验中表现较为优秀，AdaBoost则未能表现出较强的竞争力. 实验结果表明，本文提出的稳健改进算法对噪声的敏感性低于现有算法，在训练集含有噪声时具有较好的稳健性.

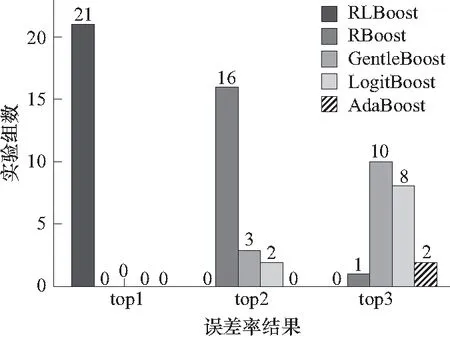
图4 不同噪声水平下的各Boosting算法误差率结果Fig.4 Statistical ranking of testing errors for Boosting algorithms with different noise levels

3.2 真实医疗数据集的稳健性验证实验

3.2.1实验数据

实验数据选用全国7省市(北京、上海、重庆、黑龙江、四川、陕西、湖南)的13家医院于2011～2012年进行老年人健康综合评估问卷调查得到的横截面数据，其中问卷由中国卫生部行业基金老年健康综合评估课题组和中国老年人保健及疾病防治联盟联合设计. 实验针对老年人跌倒发生率高，后果严重的问题进行老年人跌倒检测. 数据包含年龄、性别、是否有骨关节病、是否自发性骨折、是否尿失禁等30维特征变量，以及因记忆偏差、填写或录入错误等原因引入噪声的“近一年是否有两次以上跌倒”二分类标签，通过数据预处理，最终得到可用样本1 703组.

3.2.2评价方法

对于改进Boosting方法在真实医疗数据集上的稳健性验证实验，选择误差率、精确率、召回率和F1值4种评价指标进行对比. 误差率越低，其余3种评价指标的结果越高，则算法表现越稳健，其中误差率见式(19)，精确率、召回率和F1值为

(20)

(21)

(22)

式中TP、TN、FP和FN分别为将正类预测为正类、负类预测为负类、负类预测为正类和正类预测为负类的样本个数.

3.2.3实验结果和分析

各Boosting算法在真实医疗数据集上的不同评价指标结果如表2所示，实验参数选择见3.1.3. 实验结果表明，含有噪声的真实数据集会对算法的稳健性有较高要求，传统AdaBoost由于噪声敏感性问题的影响，不同评价指标的实验结果皆未能表现出较强竞争力. 本文提出的RLBoost的不同评价指标结果相比AdaBoost及AdaBoost的3种抗噪改进算法均有一定程度的提升，在真实的含噪数据集上表现出较好的稳健性.

表3 不同评价指标下真实医疗数据集实验结果

Tab.3 Experimental results of a real medical dataset under different evaluation criterions

评价指标AdaBoostGentleBoostLogitBoostRBoostRL-Boost误差率0.390 690.366 260.349 910.314 240.306 15精确率0.732 060.741 280.753 800.782 460.801 05召回率0.596 090.652 940.657 420.661 900.663 77F1值0.657 110.694 310.702 320.717 150.725 98

4 结 论

本文提出了结合加权KNN和自适应牛顿法的稳健Boosting方法，方法采用加权KNN进行预处理，引入所有样本的噪声先验概率. 将概率参数与Logit损失融合，构建了一种能根据噪声概率提供不同权重扩增策略的损失函数，较好地解决了指数损失和Logit损失由于函数无限增长造成的噪声样本权重不断扩增的问题. 通过自适应牛顿法进行损失函数的优化求解，使用二阶导数信息，求解出损失函数条件期望的更准确下降方向. 实验结果表明，和其他Boosting稳健改进算法相比，提出方法在不同噪声水平下均具有较高的稳健性，在真实医疗数据集上的不同评价指标结果均有一定提升. 证明了提出方法可在含噪数据中更准确地识别真实判别模式，具有一定的理论价值和应用价值.